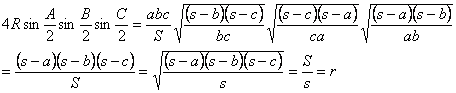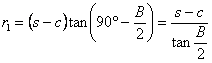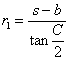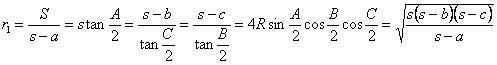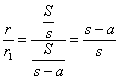■三角形の内接円と傍接円の半径に関する性質
三角形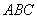において，内角を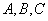，その対辺をそれぞれ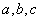とし，，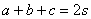
三角形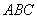の面積を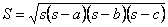，また，外接円，内接円，角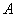内の傍接円，
角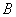内の傍接円，角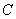内の傍接円の半径をそれぞれ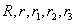とおく。

【内接円の半径】
1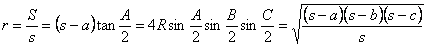　


【傍接円の半径】
2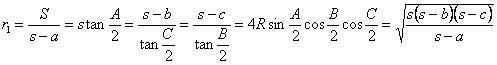　


【内接円と傍接円の半径に関する性質】
3　(1)(2)　(3)　



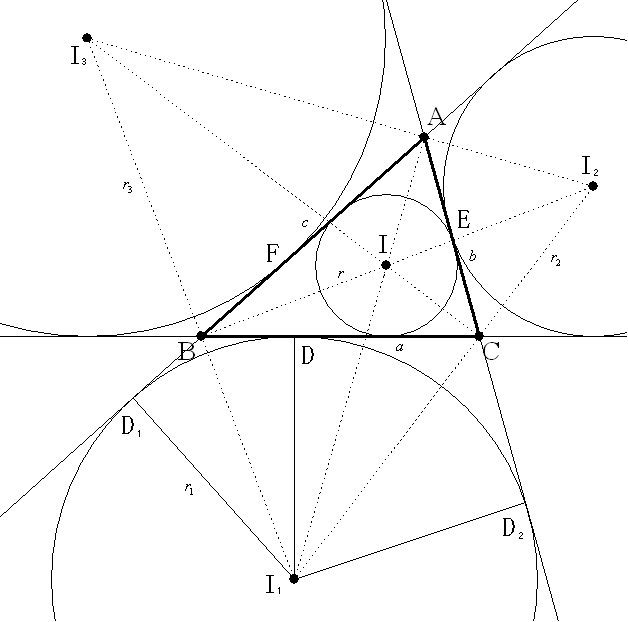
【証明】
1(1) 三角形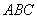の内接円の半径を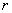とすると，

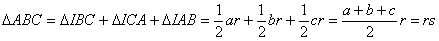
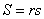∴より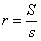
(2)　三角形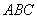の内接円と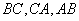との接点をそれぞれ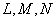とする。
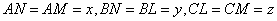とおくと，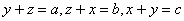
この3式を辺々加えて，両辺を2で割ると，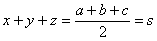
よって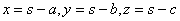，となる。
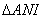において，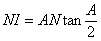
よって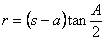，27.gif
(3)　まず，正弦定理より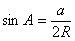であるから，
∴
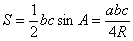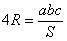次に，

同様に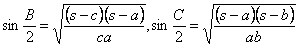，であるから，

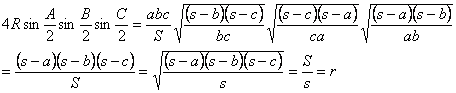
以上(1)～(3)より，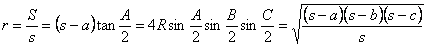

2(1)　面積を考える。
四角形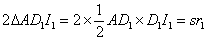＝＋四角形＋四角形･･･①
四角形＝･･･②
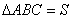･･･③
四角形＋四角形＝
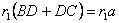＝･･･④
①に②，③，④を代入すると，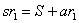
よって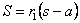，より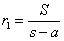
(2)は直角三角形で，であるから，
(3)　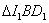は直角三角形で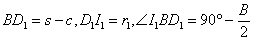，であるから，
　
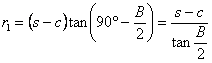
また，も直角三角形で，同様に，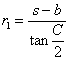
　　
(4)　
同様に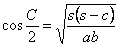，であるから，

以上(1)～(4)より，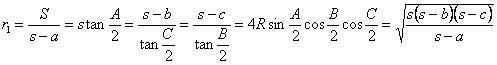
3(1)　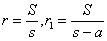であるから，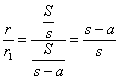
(2)　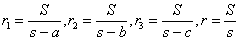であるから

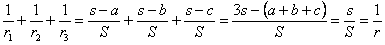
(3)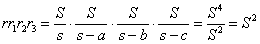
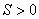より，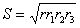
次に，(2)の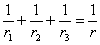の両辺に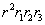を掛けると

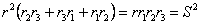
よって，両辺の平方根をとると
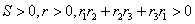であるから

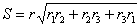
【終証】（2009.11.21/Update 2009.12.27）