| 【問題】ひもを2つに切り、一方で円を、もう一方で正方形を作る。 このとき、円と正方形の面積和を最小にするには、ひもをどの様に切ればよいか。 |
| 【解】ひもの長さを | とする。 |
| ひもを水平に置き、左から | の長さのところで2つに切り、長さ | の方で円を、 |
| 長さ | の方で正方形を作るものとする。 | である。 |
| 円の半径を | とすると、 | より | 。 |
| 正方形の一辺の長さを | とすると、 | より | 。 |
| ここで、円と正方形の面積和を | とおくと、 |
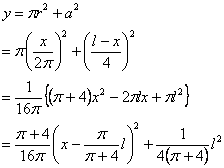
| は | についての2次関数で、そのグラフは下に凸の放物線であるから、 |
| のとき、 |
| その面積和の最小値は | となる。 |
| このとき、 | である。 |
| 【答】ひもを | に内分するところで切って、 | の比の長さで切ったひもで円を、 |
| 残りのひもで正方形を作ったとき、その面積和は最小となる。 |