|
展開例
| n | 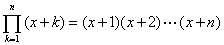 |
| 1 | 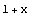 |
| 2 | 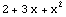 |
| 3 | 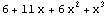 |
| 4 | 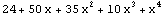 |
| 5 | 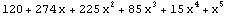 |
| 6 | 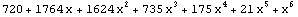 |
| 7 | 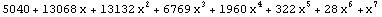 |
| 8 | 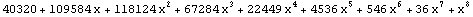 |
| 9 | 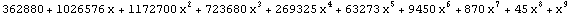 |
| 10 | 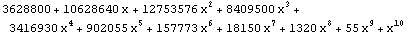 |
| 11 | 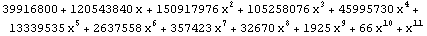 |
| 12 | 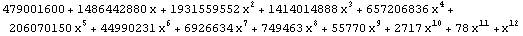 |
| 13 | 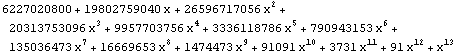 |
| 14 | 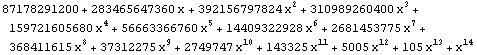 |
| 15 | 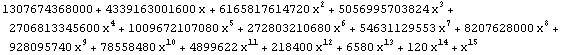 |
| 16 | 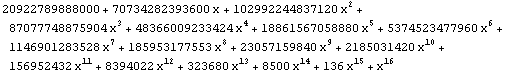 |
| 17 | 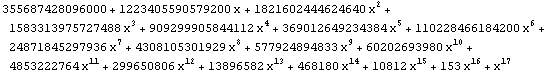 |
| 18 | 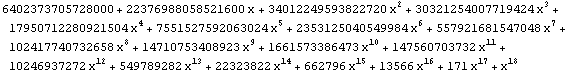 |
| 19 | 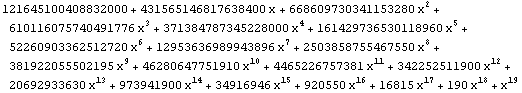 |
| 20 |  |
| 21 |  |
| 22 |  |
| 23 | 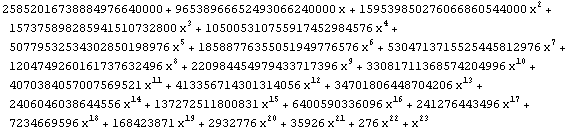 |
| 24 | 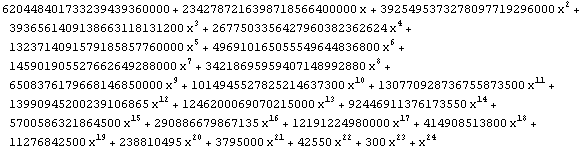 |
| 25 |  |
| 26 |  |
| 27 |  |
| 28 |  |
| 29 |  |
| 30 |  |
各項の係数の求め方(一例)
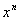 の係数は、1である。 の係数は、1である。
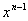 の係数は の係数は
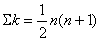
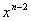 の係数 の係数
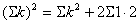 より、 より、
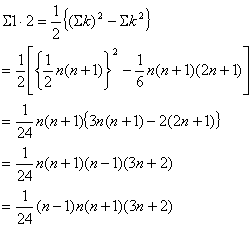
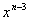 の係数 の係数
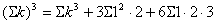 ・・・① ・・・①
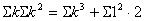 より、 より、
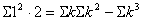
これを①に代入すると、
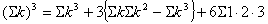
よって、
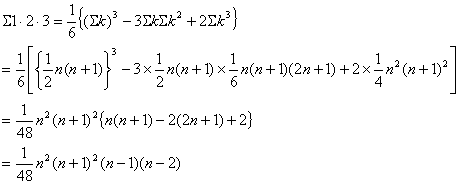
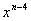 の係数 の係数
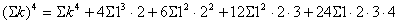 ・・・① ・・・①
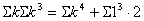 より、 より、
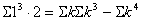 ・・・② ・・・②
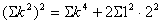 より、 より、
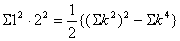 | ・・・③ |
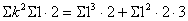 | に | 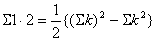 | と②を代入 |
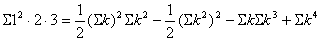 | ・・・④ |
②~④を①に代入
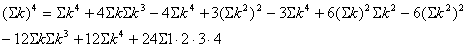
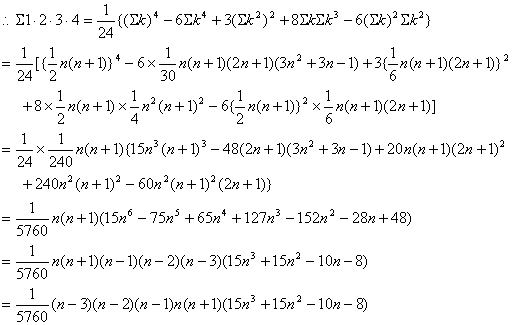
このような方法では、次の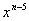 の係数を求めるのは大変である。 の係数を求めるのは大変である。
今までの計算結果より、一般に、
| となることが帰納的に予測できる。ただし、 | 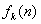 | は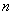 の の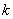 次式である。 次式である。 |
|
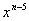 の係数は、 の係数は、
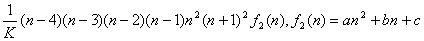 | とおける。 |
分母の最小公倍数が5760であるから、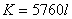 と置いた。 と置いた。
①~③の連立3元1次方程式を解くと、
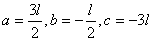
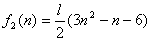
ここで、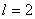 と置くと、 と置くと、
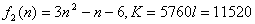
∴ 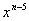 の係数は、 の係数は、
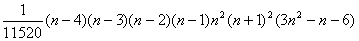
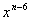 の係数は、 の係数は、
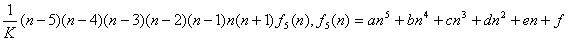 | とおける。 |
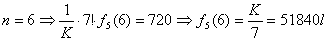 | ・・・① |
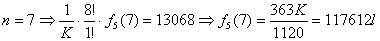 | ・・・② |
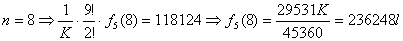 | ・・・③ |
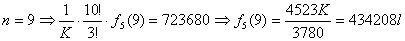 | ・・・④ |
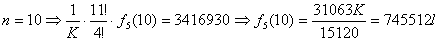 | ・・・⑤ |
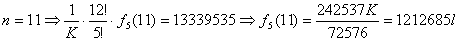 | ・・・⑥ |
分母の最小公倍数が362880であるから、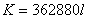 と置いた。 と置いた。
①~⑥の連立6元1次方程式を解くと、
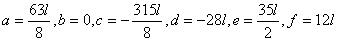
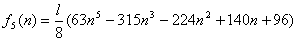
ここで、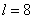 と置くと、 と置くと、
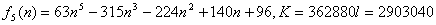
∴ 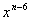 の係数は、 の係数は、
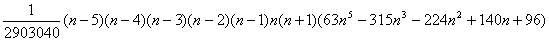
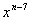 の係数は、 の係数は、
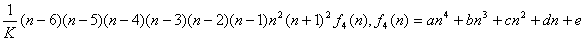 | とおける。 |
分母の最小公倍数が725760であるから、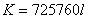 と置いた。 と置いた。
①~⑤の連立5元1次方程式を解くと、
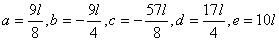
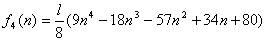
ここで、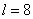 と置くと、 と置くと、
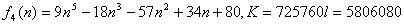
∴ 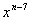 の係数は、 の係数は、

- 定数項は、
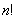 である。 である。
(2002.10.28/Update2009.12.22)
別の計算方法で,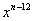 までの係数を求めました。こちら(PDF) までの係数を求めました。こちら(PDF)
(Update2011.03.03)
|