| (1) | (2) | (3) | (4) |
| (1) |  |
(2) |  |
(3) |  |
| (1) |  |
(2) |  |
このとき,AB+CDE+FGHI=2005を満たす数式は何通りあるか.
ただし,A~Iはすべて異なる数字とする.
[{(a-b)3+(b-c)3+(c-a)3}/3][{(a-b)7+(b-c)7+(c-a)7}/7]=[{(a-b)5+(b-c)5+(c-a)5}/5]2
|
1辺の長さが1である正方形ABCDがある.この正方形に含まれる3つの円P,Q,Rを考える. 円Pは正方形の2辺BA,BCに接しており,円Qは2辺CB,CDに接しており,円Rは2辺AD,ABに接している. また,円Pは他の2つの円に外接しており,さらに円Qと円Rの半径の長さは等しいものとする. このとき,△PQRが正三角形になるときの円Pの半径の長さを求めよ. | 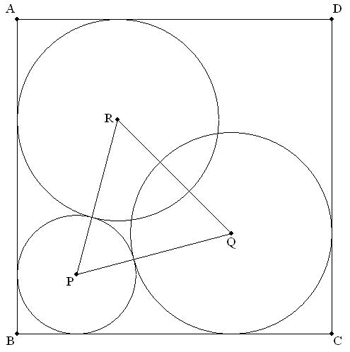 |
| 4点 | について, |
| 2直線 | の交点の軌跡を求めよ. |
△ABCの内接円と3辺BC,CA,ABとの接点をそれぞれD,E,Fとする.
(△ABCの内接円の面積)/(△ABCの外接円の面積)=1/9のとき,(△DEFの面積)/(△ABCの面積)の値を求めよ.
|
互いに外接している3つの円の中心をO1,O2,O3 , 半径を r1=2,r2=3,r3=4とする. 以下各円を次のように定義する. 円O1,O2,O3のすべてと外接する円の中心をO0 , 半径をr0 , 円O1,O2,O3のすべてと内接する円の中心をO4 , 半径をr4 , 円O2,O3 に外接し,円O4 に内接する円のうち, 円O1 と異なる円の中心をO5 ,半径をr5, 円 O1,O3に外接し,円O4 に内接する円のうち, 円O2 と異なる円の中心をO6 ,半径をr6 , 円O1,O2 に外接し,円O4に内接する円うち, 円O3 と異なる円の中心をO7 ,半径をr7, 円O3,O5 に外接し,円O4に内接する円うち, 円O2 と異なる円の中心をO8 ,半径をr8 とする. このとき,各円の半径r0,r4~r8を求めよ. | 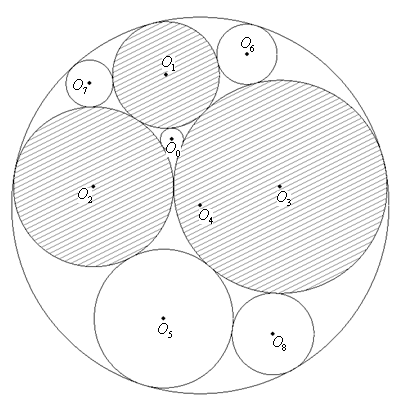 |
|
nを正の整数とし, 一辺の長さが(2n+4)の正三角形ABCがある. 頂点Aを中心とする半径nの円, 頂点Bを中心とする半径(n+1)の円, 頂点Cを中心とする半径(n+2)の円 について,次の問いに答えよ. (1) 3つの円に外接する円Pの半径rを求めよ. (2) 3つの円を内接する円Qの半径Rを求めよ. | 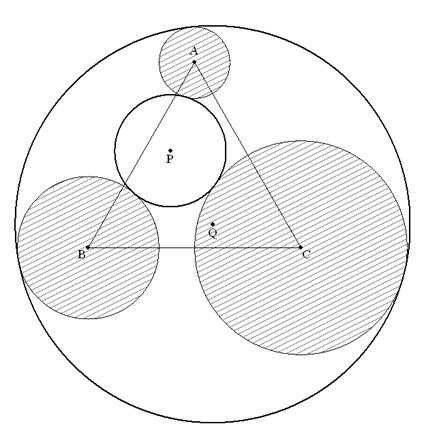 |
| 四角形ABCDは条件AB=DC,AD<BC,∠ABC=α,∠DCB=β(α<β)を満たす。 また,辺AD,BCの中点をそれぞれM,N,また,BAとNMの交点をP,CDとNMの交点をQ,BAとCDの交点をRとする。 (1) △PQRは二等辺三角形となることを証明せよ。 (2) ∠MNCをα,βを用いて表せ。 | 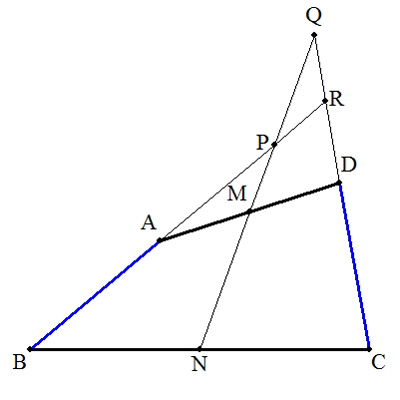 |
|
正方形ABCDは折り紙で,E,FをそれぞれAB,DC上の点とし, EFで折り返したとき,頂点AがBC上の点Gに移り,BE=BGとなった。 また,頂点Dは点Hに移り,GHとDCの交点をIとし,J,KはそれぞれEI, GCの中点である。このとき,∠GKJの大きさを求めよ。 | 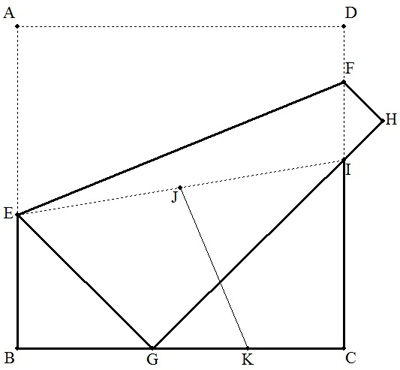 |
|
正方形ABCDのCD,DA上あるいはその延長上にそれぞれ点E,Fを ∠CBE=∠EBFとなるようにとる。また,BF上に点Gを,FA=FGと なるようにとり,点H,I はそれぞれGE,BCの中点,BEとHIの 交点をJとする。このとき,次の問いに答えよ。 (1) ∠CBE=25°のとき,∠BJIの大きさを求めよ。 (2) ∠CBEが0°から90°まで変化すると,点Jはどのような軌跡を描くか。 | 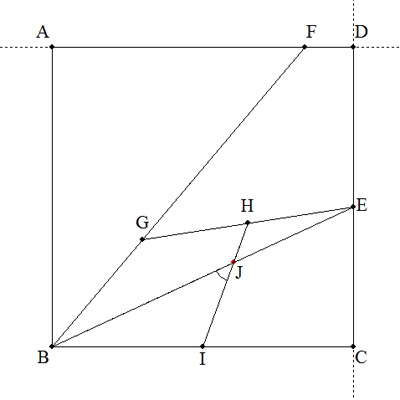 |
|
平行四辺形ABCDにおいて,BE=aBC(0<a<1), CF=bCD(0<b<1),DG=cDA(0<c<1), AH=dAB(0<d<1),AEとBFの交点をP,BFとCG の交点をQ,CGとDHの交点をR,DHとAEの交点をSとす るとき,四角形PQRS/平行四辺形ABCDの値を求めよ。 | 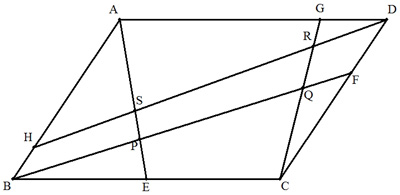 |
三角形ABCの3辺の長さが次の場合のとき,その面積を求めよ。
(1) a=(α-β)(αβ+γ2),b=β(α2+γ2),c=α(β2+γ2)。ただし,α>βとする。
(2) a=(α+β)(αβ-γ2),b=β(α2+γ2),c=α(β2+γ2)。ただし,αβ>γ2とする。
|
C=90°の直角三角形ABC(BC=a,CA=b,AB=c )について, BCを軸として1回転してできる立体の体積をV1,表面積をS1, CAを軸として1回転してできる立体の体積をV2,表面積をS2, ABを軸として1回転してできる立体の体積をV3,表面積をS3 とする。 このとき,次の比を求めよ。 (1) V1:V2:V3 (2) S1:S2:S3 | 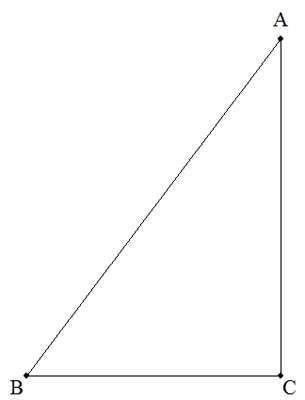 |
|
△ABCにおいて,BCを3:1に内分する点をD,ABを3:7に内分する点をE, CA上に2点F,Gをこの順にとり,DFとEGの交点をHとすると,DF:FH=4:5 であった。また,GHを3:2に内分する点をI,EBを4:3に内分する点をJ, IJとFGの交点をKとするとき,次の比を求めよ。 (1) EG:GH (2) IK:KJ | 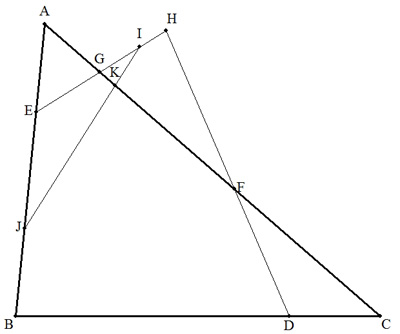 |
|
BC=7,CA=5,AB=6である△ABCの辺BC,CA,AB上にそれぞれ点D,E,FをBD=3,CE=2,AF=1となるようにとる。また,BEとCFの交点をP,CFとADの交点をQ,ADとBEの交点をRとするとき,次の面積比を求めよ。 (1) △DEF:△ABC (2) △PQR:△ABC | 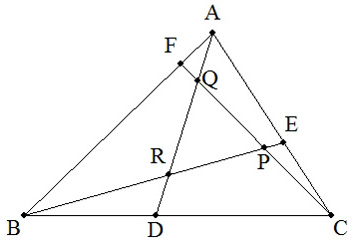 |
|
四角形ABCDに対して, △BCD,△ACD,△ABD,△ABCの重心をそれぞれE,F,G,H, 辺AB,BC,CD,DAの中点をそれぞれI,J,K,Lとする。 このとき,四角形EFGHと四角形IJKLの面積比を求めよ。 | 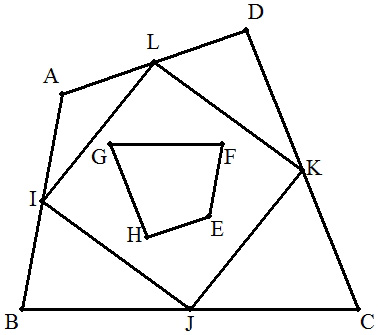 |
0から9までの数字が書かれたカードが1枚ずつ合計10枚ある。
これらのカードで,5桁の数と4桁の数と1桁の数を作り,
□□□□□÷□□□□=□となるようにせよ。
5桁の数の2乗が1~9までの数字が使われる9桁の数となった。このような5桁の数を求めよ。
ある自然数nに対して,n3-n2を計算すると,1~9までの数字が使われる9桁の数となった。nを求めよ。
|
四角形ABCDにおいて,8点E,F,G,H,I,J,K,Lは各辺の3等分点である。 また,LGとEJ,FIの交点をそれぞれP,Q, KHとEJ,FIの交点をそれぞれS,Rとする。 このとき,四角形PQRSと四角形ABCDの面積比は1:9となることを証明せよ。 | 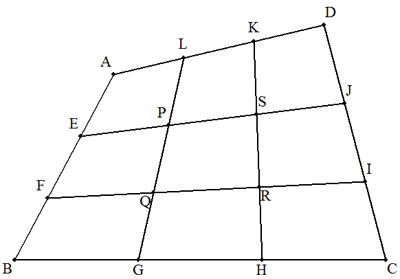 |
3辺の長さがa=4γ(αβ-γ2)(α+β),b=4βγ(α2+γ2),c=4αγ(β2+γ2)である三角形ABCの内接円,外接円の半径をそれぞれ求めよ。ただし,α>β≧γとする。
|
三角形ABCはAB=AC,BC=17の二等辺三角形である。 いま,BC上に点DをBD=13となるようにとり, 線分ADを7:1に外分する点をEとすると, AE=ABであった。 このとき,AEの長さを求めよ。 | 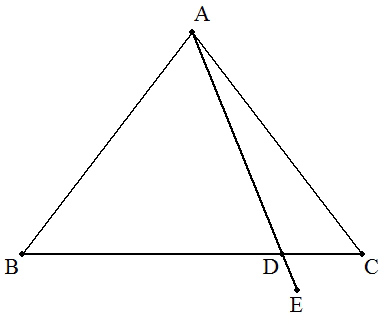 |
| (1) | 一辺aの正方形に図のように内接する3個の合同な正方形の一辺の長さを求めよ。 | 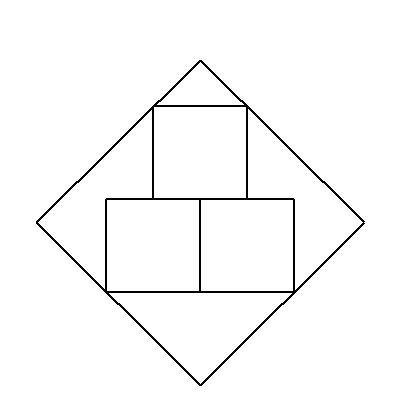 |
| (2) | 一辺aの正三角形に図のように内接する3個の合同な正方形の一辺の長さを求めよ。 | 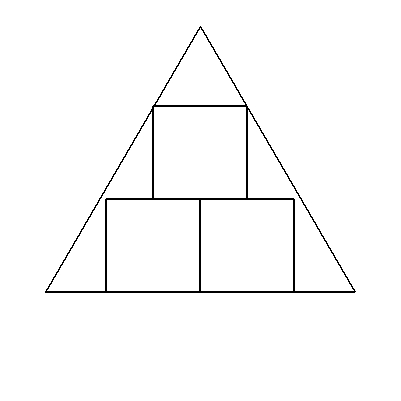 |
| (3) | 半径rの円に図のように内接する3個の合同な正方形の一辺の長さを求めよ。 | 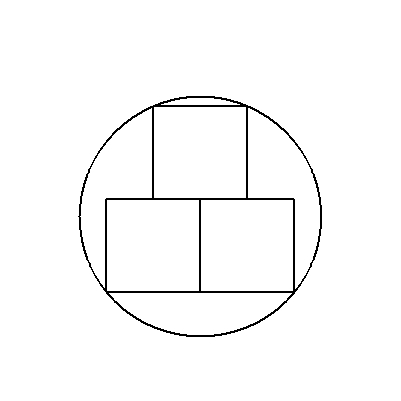 |
| (4) | 一辺aの正五角形に図のように内接する3個の合同な正方形の一辺の長さを求めよ。(高校生向け) | 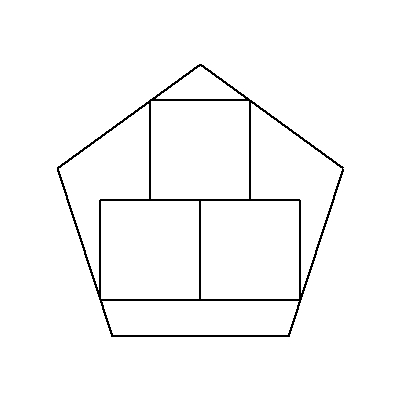 |
| (5) | 一辺aの正六角形に図のように内接する3個の合同な正方形の一辺の長さを求めよ。 | 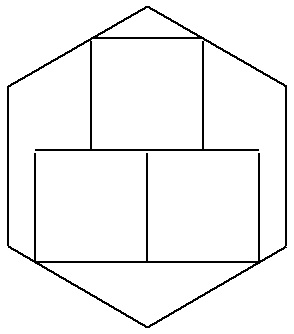 |
|
底辺BC=a,高さAH=hの三角形ABCに,図のように正方形DEFGが内接している。 (1)正方形の作図の方法を述べよ。 (2)正方形の1辺をa,h を用いて表せ。 | 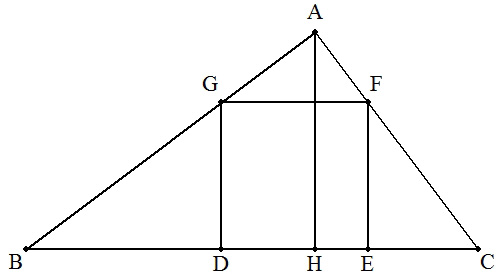 |
|
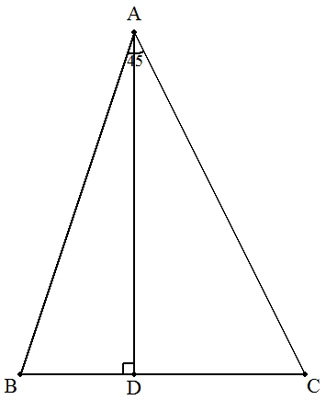
∠A=45°の△ABCの頂点Aから対辺BCに垂線ADを引くとき,△ABCの面積を求めよ。 (1) BD=2 ,CD=3 のとき (2) BD=p ,CD=q のとき |
 |
| (1) 1組の2つの三角定規を図のように直角の部分で重ねるとき, 2つの三角形の重なった部分(四角形BCDF)の面積を求めよ。 ただし,2つの三角形の辺のうち,等しい辺の長さをaとする。 すなわち,AB=EC=aである。 | 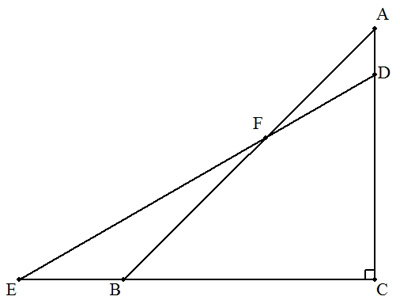 |
| (2) 1組の2つの三角定規を図のように重ねるとき, 2つの三角形の重なった部分(四角形BCGF)の面積を求めよ。 ただし,2つの三角形の辺のうち,等しい辺の長さをaとする。 すなわち,BC=DE=aである。 | 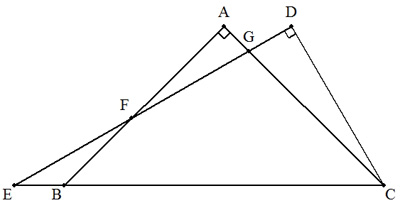 |
|
凹四角形ABCDにおいて,AB=CD=12,∠DAB=45°,∠ABC=75°, ∠BCD=15°であるとき,四角形の面積を求めよ。 | 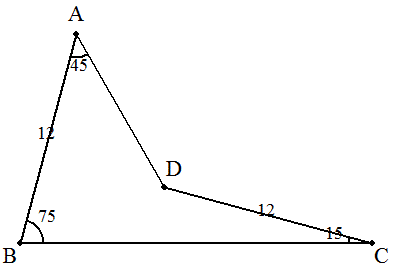 |
|
△ABC内に点Dをとる。 BC=7,CA=6,AB=5,BD=4,CD=5のとき,ADの長さを求めよ。 | 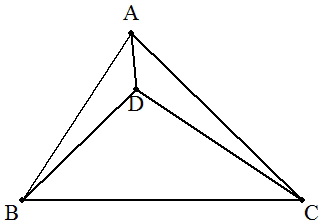 |
|
平行四辺形ABCD内に点Eをとる。 AB=4,BC=5,AE=BE=CE=3のとき,DEの長さを求めよ。 | 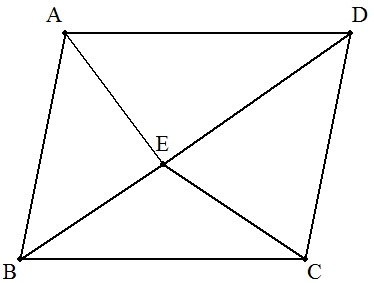 |
|
五角形ABCDE内に点Fをとる。 AB=AE=5,BC=DE=4,CD=6,BF=CF=DF=EF=4のとき,AFの長さを求めよ。 | 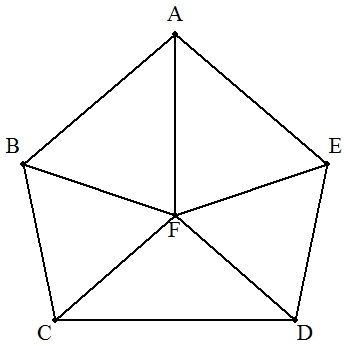 |
|
(1) 正方形ABCDの内部に点Eをとる。 AE=3,BE=1,CE=2のとき,ABの長さを求めよ。 | 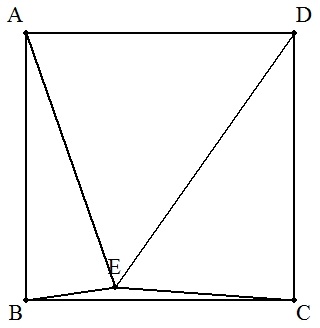 |
|
(2) 正方形ABCDの外部に点Eをとる。 AE=3,BE=1,CE=2のとき,ABの長さを求めよ。 | 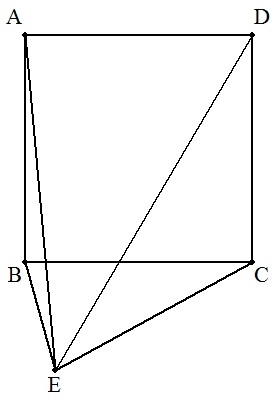 |
|
(3) 正方形ABCDの内部に点Eをとる。 AE=p,BE=q,CE=rのとき,ABの長さを求めよ。 ただし,(p~r)/√2<q<(p+r)/√2とする。 | 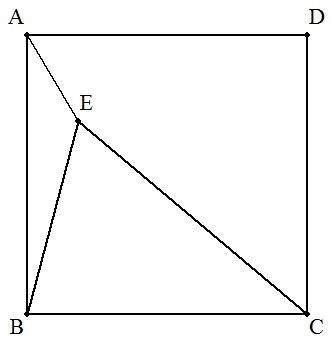 |
| (1) 3円A,B,Cについて,2円ずつの共通外接線の交点P,Q,Rは,1直線上にあることを証明せよ。 | 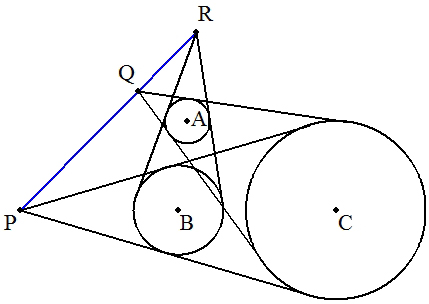 |
|
(2) 3円A,B,Cについて,2円B,Cの共通外接線の交点をP, 2円C,Aの共通内接線の交点をQ,2円A,Bの共通内接線の交点をRとすると, 3点P,Q,Rは1直線上にあることを証明せよ。 | 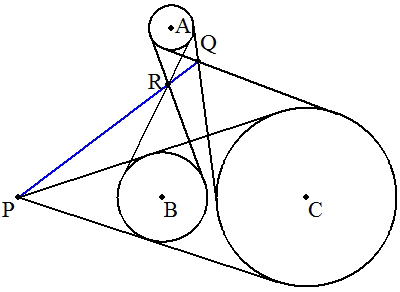 |
|
AB=25,BC=65,CD=33の四角形ABCDの対角線の交点をEとする。 ∠BAC=∠BDC=90°のとき,AEの長さを求めよ。 | 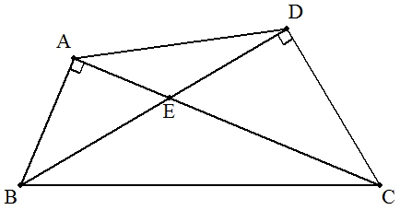 |
|
1辺が10の正三角形ABCの内部に点Pをとり, Pから辺BC,CA,ABに下ろした垂線の足を それぞれD,E,Fとする。 AF=6,BD=7のとき,次の長さを求めよ。 (1) CE(中学生向け) (2) PD (3) △DEFの内接円の半径 | 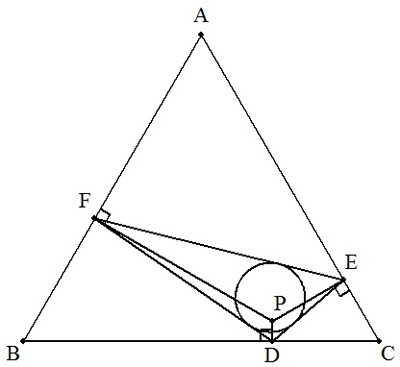 |
| (1) | 一辺aの正方形の中に合同な正方形を図のようにn段内接させる(図は3段)。 合同な正方形の一辺の長さを求めよ。 | 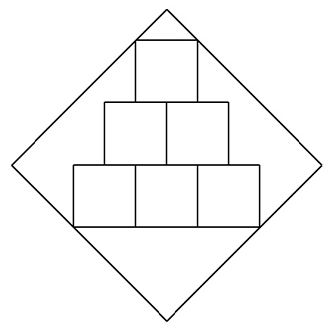 |
| (2) | 一辺aの正三角形の中に合同な正方形を図のようにn段内接させる(図は3段)。 合同な正方形の一辺の長さを求めよ。 | 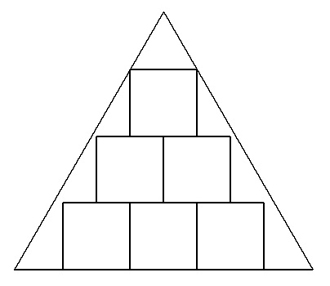 |
| (3) | 半径rの円の中に合同な正方形を図のようにn段内接させる(図は3段)。 合同な正方形の一辺の長さを求めよ。 | 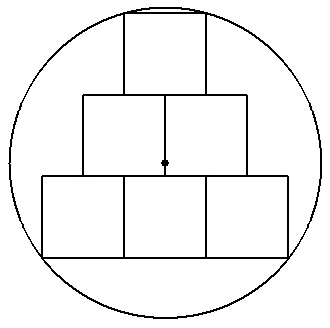 |
| (4) | 一辺aの正五角形の中に合同な正方形を図のようにn段内接させる(図は3段)。 合同な正方形の一辺の長さを求めよ。 | 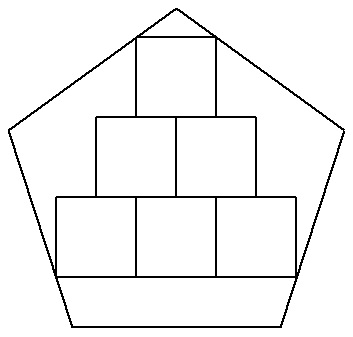 |
| (5) | 一辺aの正六角形の中に合同な正方形を図のようにn段内接させる(図は3段)。 合同な正方形の一辺の長さを求めよ。 | 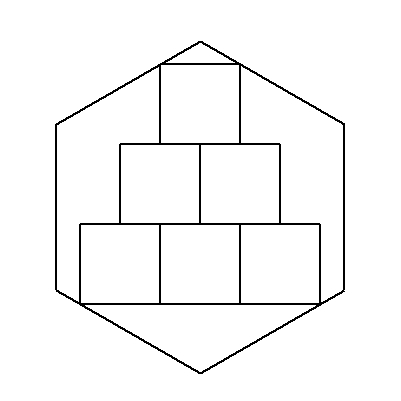 |
|
右の図のような扇形OABがある。 ∠AOBの2等分以外の方法で,扇形の面積を2等分したい。 (1) その作図方法を示しなさい。 (2) その作図が正しいことを証明しなさい。 | 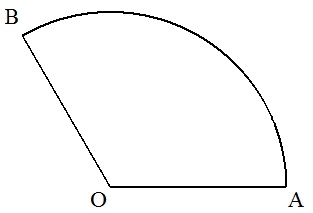 |
| AB=a ,BC=b ,CD=c である四角形ABCDの面積を最大にするDAの長さをx とおく。 (1) xの満たす3次方程式を求めよ。 (2) a,b,c,xの正の整数解をいくつか求めよ。 ただし,(a-b)2+(b-c)2+(c-a)2≠0 とする。 | 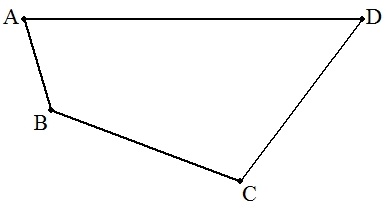 |
| AB=1である長方形ABCDにおいて, 図のように三角形ABDの内接円Iの面積と 三角形BCDに内接する正方形CEFGの面積が 等しくなるとき,BCの長さを求めよ。 ただし,AB<BCとする。 | 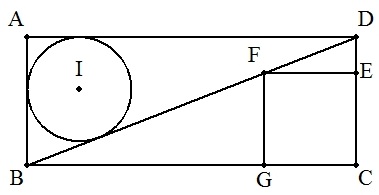 |
| ∠A=90°である△ABCの辺BC上に内接正方形DEFGをつくり, AD,AEとGFとの交点をそれぞれH,Iとする。 このとき,GI2+FH2+HI2=GF2を証明せよ。 | 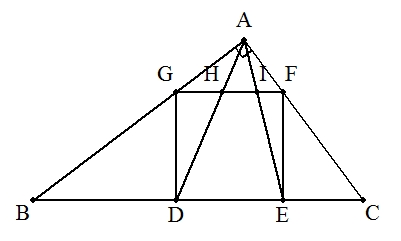 |
| (1) | 1辺aの正五角形ABCDEの中に正三角形AGFを図のように内接させる。 ただし,CD∥FGとする。 正三角形の1辺の長さを求めよ。 | 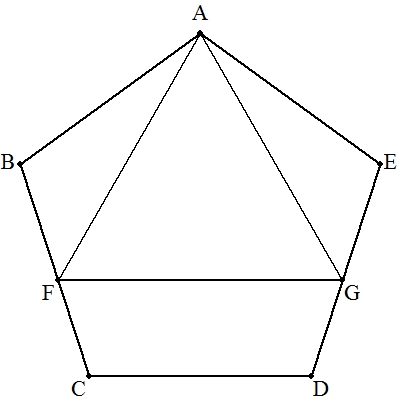 |
| (2) | 1辺aの正五角形ABCDEの中に正三角形FGHを図のように内接させる。 ただし,CD∥HGとする。 正三角形の1辺の長さを求めよ。 | 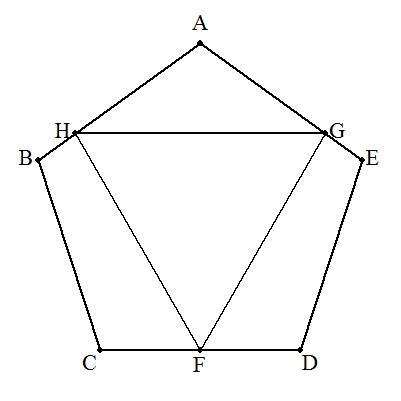 |
| (3) | 1辺aの正五角形ABCDEの中に正方形PQRSを図のように内接させる。 ただし,CD∥QRとする。 正方形の1辺の長さを求めよ。 | 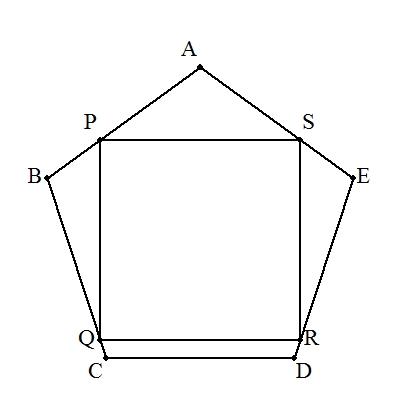 |
| 四角形ABCDは1辺a+2bの正方形である(a>0,b>0 )。 BC上に2点E,FをBE=a ,EH=b となるように,AD上に点GをDG=b となるように, GH上に点IをGI=b となるようにとり,AIの延長とDCの交点をFとする。 このとき,次の問いに答えよ。 (1) ∠EAFの大きさを求めよ。 (2) DFの長さを求め,BE:EC=CF:2FDを証明せよ。 | 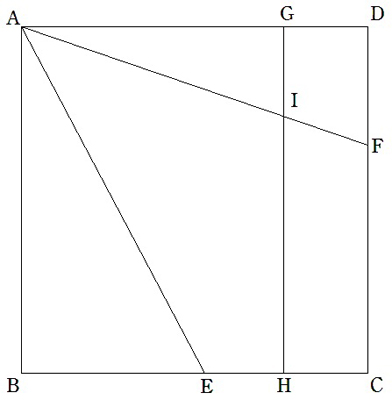 |
| (1) | (中学生向け) 1辺の長さが1の正方形の1辺と辺を共有して 正三角形を正方形の外側にかき, さらに図のように,円を外接させる。 円の半径を求めよ。 | 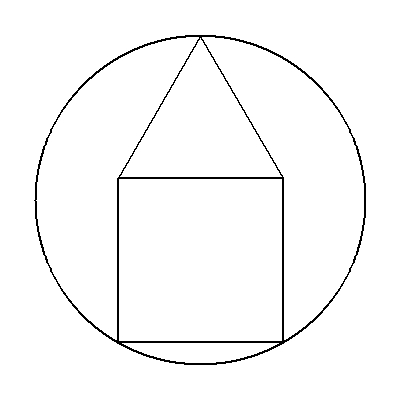 |
| (2) | (中学生向け) 図のように,1辺の長さが1の正方形の周りに正三角形をかき, さらに円を外接させる。 円の半径を求めよ。 | 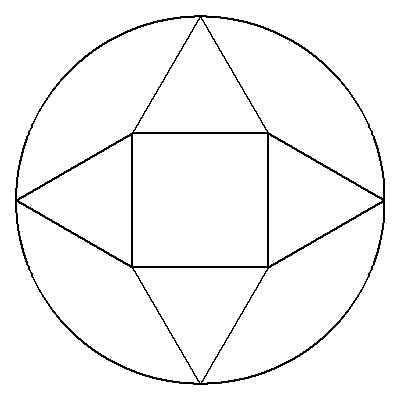 |
| (3) | 図のように,1辺の長さが1の正五角形の周りに正方形と正三角形をかき, さらに円を外接させる。 円の半径を求めよ。 | 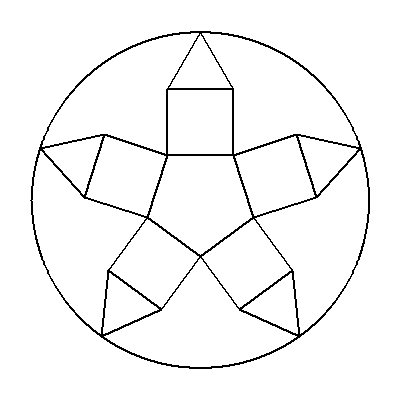 |
| (4) | 1辺の長さが1の正六角形の周りに正五角形,正方形,正三角形をかき, さらに円を外接させる。 円の半径を求めよ。 ただし,図は正六角形の1辺に正五角形をかいた場合の部分図である。 | 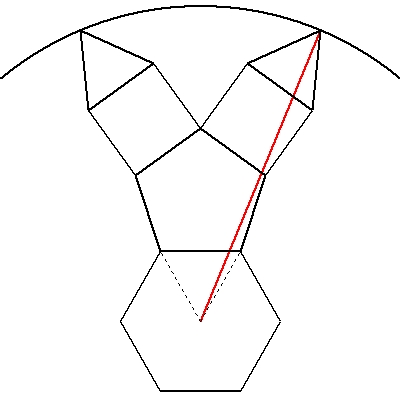 |
| (1) |
∠A=90°の直角三角形ABCの頂点AからBCに下ろした垂線の足をDとし, △ABDと△ACDにそれぞれ内接正方形DEFG,DHIJをつくる。 このとき,AF=AIを証明せよ。 | 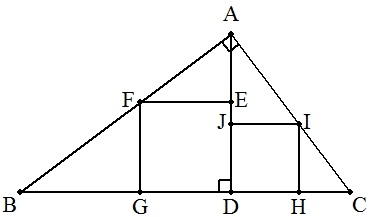 |
| (2) |
∠A=90°の直角三角形ABCの頂点AからBCに下ろした垂線の足をDとする。 △ABDと△ACDの内接円の面積の和は,△ABCの内接円の面積に等しいことを証明せよ。 | 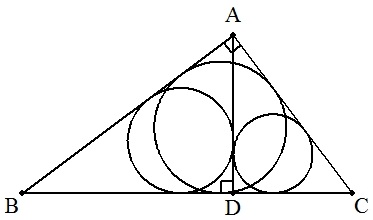 |
| △ABCの辺BCの中点をDとする。また,AC,AB上にそれぞれ点E,Gを, △ABC内に点Fをとると,四角形DEFGが正方形になるという。 このとき,AE=p,EC=q,AG=r,GB=sとおくとき,GDの長さを求めよ。 | 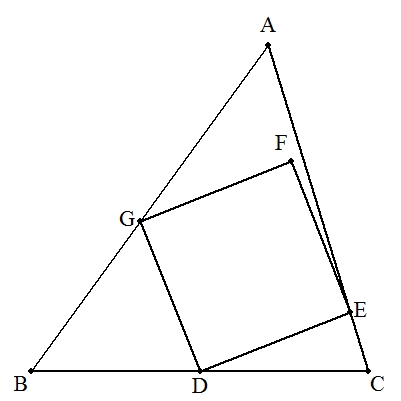 |
|
1辺の長さが15の正方形の折り紙ABCDにおいて, 頂点Aを辺BC上の点Gに重ねて折るとBG=8であった。 このとき,頂点DはHに移り,折り目をEF, GHとCDとの交点をIとする。 (1) EFの長さを求めよ。 (2) △FIHの面積を求めよ。 | 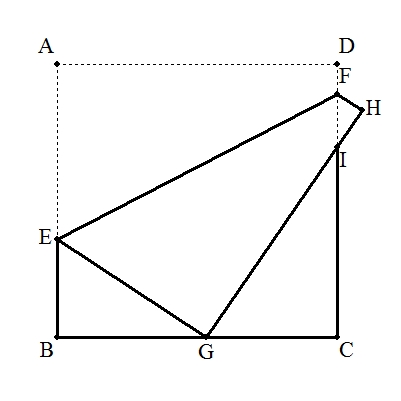 |
|
正方形の折り紙ABCDにおいて,頂点AをBC上の点Gに重ねて折ったとき, 頂点DはHに移り,折り目をEF,GHとCDとの交点をIとする。 さらに,△IGCの内接円Jと各辺との接点を図のようにK,L,Mとする。 このとき,次を証明せよ。 (1) BG=IM,GL=DI,LC=IH (2) LC・BC=BG・GL | 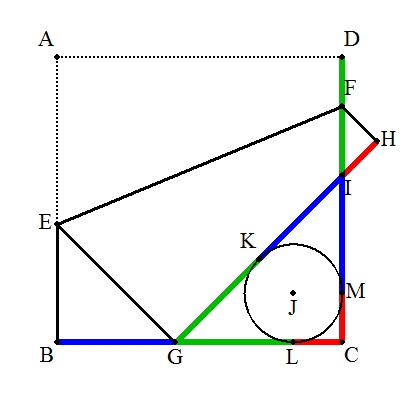 |