■趣味の数学問題集・Ａ問題

  1. (1)
    長方形の紙片ABCDの頂点Aが辺BC上の点Eと重なるように折り曲げる。
    このとき，折り目の線分GHの長さを求めよ。
    ただし，AB＝a，BC＝b（a＞b），BE＝kb（0＜k＜1）とする。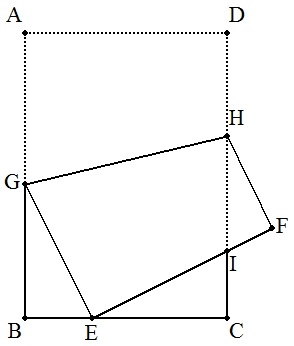
    (2)
    長方形の紙片ABCDの頂点Aが辺BC上の点Eと重なるように折り曲げる。
    このとき，折り目の線分FDの長さを求めよ。
    ただし，AB＝a，BC＝b（a＜b）とする。
    また，AB，BC，FDの長さが整数になる例を1つ求めよ。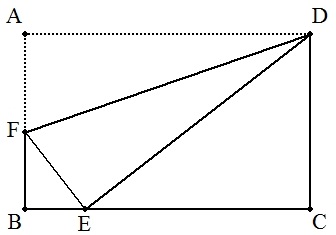

  2. ∠C＝90°の直角三角形ABCがBを1つの頂点とする正方形BDEFに
    図のように内接している。
    (1)　BC＝a，CA＝bのとき，正方形の1辺の長さを求めよ。
    (2)　BC，CA，BDの長さが整数となる例をいくつか求めよ。
    (3)　4つの直角三角形ABC，CBD，ACE，BAFの内接円の半径をそれ
    　ぞれr1，r2，r3，r4とするとき，AE＝r1＋r2＋r3－r4を証明せよ。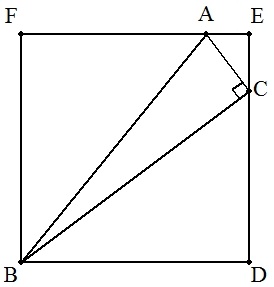
  3. （中学生向け）
    (1)　 AD//BC，BC⊥DCである台形ABCDがあり，辺AB上に
    1辺をもつ正方形AEFGが図のように内接している。
    BC＝xをAD＝y，DC＝zを用いて表せ。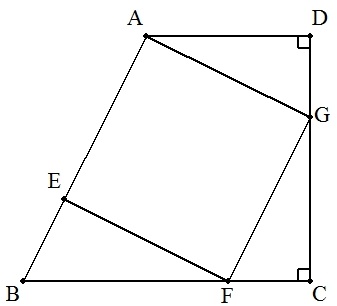
    (2)　 AD//BC，BC⊥DCである台形ABCDがあり，図のように
    円Iが内接している。
    円の半径rをBC＝x，AD＝yを用いて表せ。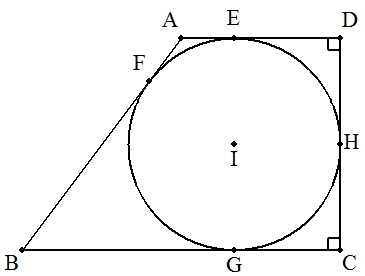

  4. 半径aの円Oがあり，平面上に固定されている。
    (1)　 右の図のように，円Oの外側の周りを半径bの円Pが，
    点Aの位置から滑ることなく回転しながら1周するとき，
    円Pは何回転するか。ただし，a，bは自然数とする。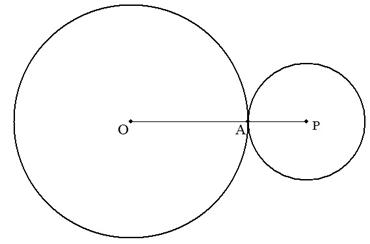
    (2)　 右の図のように，円Oの内側の周りを半径bの円Qが，
    点Aの位置から滑ることなく回転しながら1周するとき，
    円Qは何回転するか。ただし，a，bは自然数でとする。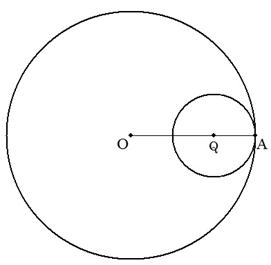
  5. （中学生向け）
    ある中学生が計算問題を作りました。
    次の計算をして，答を下から選びなさい。
    280×15÷24＋5×25÷12.85＝？

    (1) 約419.859　(2) 約284.668　(3) 約350.194
    答　(3)






    さて，上の問題は間違っていて，計算問題を正しいとすると，答は，約184.728となり，答の3択の中から選択できません。
    答の3択の中で，約350.194を答にしているので，そのような答になるためには，計算問題が間違っていることになります。
    与えられた計算問題を少し手直しして，正しい計算問題をつくりなさい。
    ただし，数字を直したり，数字の順番を入れ替えたりはしないものとします。

  6. （中学生向け）
    ある△ABCの辺BCに関して，点Aと反対側に点Dを，BC=CD，CA=AD，AB=BDとなるようにとる。
    1/a+1/b=1/cのとき，∠BCAを求めよ。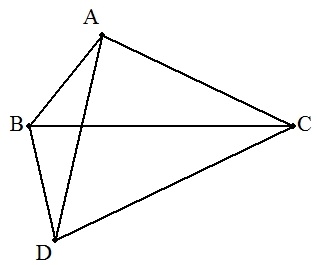

  7. 線分ABにやや足りない直線定規だけを用いて，線分ABを引け。







  8. 正七角形ABCDEFGについて，AB=a，AC=b，AD=cとする。
    (1)　1/b+1/c=1/aを証明せよ。
    (2)　b/a=xとおくと，x3-x2-2x+1=0となることを証明せよ。
    (3)　c/a=yとおき，yの満たす3次方程式を求めよ。ただし，y3の係数は1とする。
    (4)　c/b=zとおき，zの満たす3次方程式を求めよ。ただし，z3の係数は1とする。
    (5)　b2/a2+c2/b2+a2/c2の値を求めよ。
    (6)　a2/b2+b2/c2+c2/a2の値を求めよ。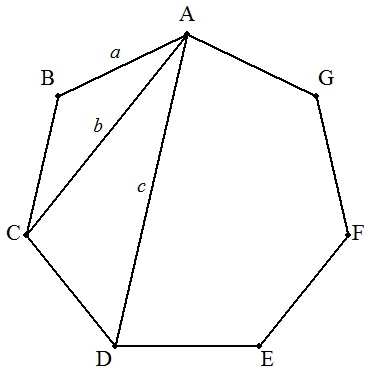
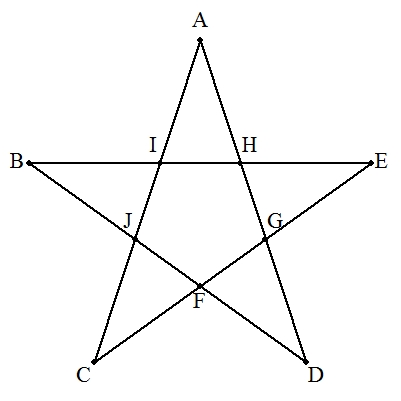
  9. （中学生向け）
    右の星形ABCDEには重なりのない三角形が5個ある。
    (1)この星形に2本の直線を引いて，重なりのない三角形を9個つくれ。
    (2)この星形に2本の直線を引いて，重なりのない三角形を10個つくれ。
  10. （中学生向け）
    直角三角形ABCの外接円O(Ｒ)，内接円P(r)に対して，
    BCの中点Mに接して，円Oに内接する円Qの半径がrのとき，
    rをRを用いて表せ。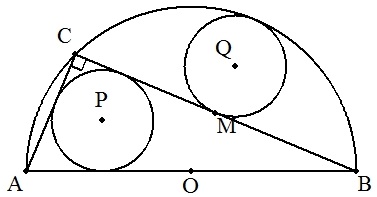

  11. 1/4円OABに円Cが内接している。図のように
    1/4円に内接し円Cに外接する円の中心Qから
    OCに下ろした垂線の足をPとする。このとき，
    (1)　OQ+QP=2OPを証明せよ。
    (2)　OA＝aとするとき，円Qの半径rを求めよ。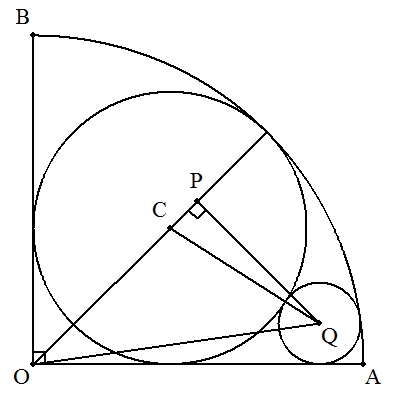
  12. （中学生向け）
    線分AB上に点Cをとり，AB，BC，CAを直径とする大円，
    中円，小円をつくる。
    点Cを通り，ABに垂直な大円の弦をDEとする。
    点CをAB上のどこにとっても，DEの長さが一定であれば，
    斜線部分の面積も一定であることを証明せよ。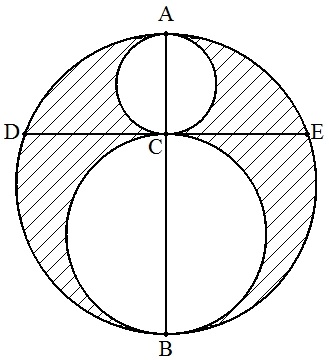
  13. （中学生向け）
    (1)線分AD上に4個の半円が図の様に配置されている。
    斜線部分の面積Sが次式で与えられることを証明せよ。
    S=πBC・AD/4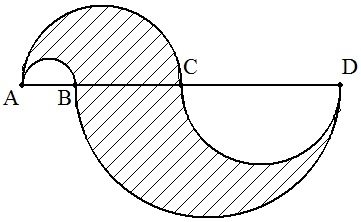
    (2)　線分AF上に6個の半円が図の様に配置されている。
    斜線部分の面積Sが次式で与えられることを証明せよ。
    S＝π（BC・AD+DE・BF）/4=π（BC・AE+DE・CF）/4

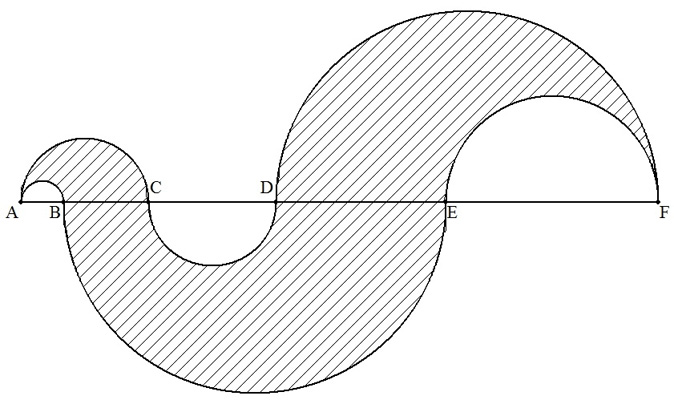
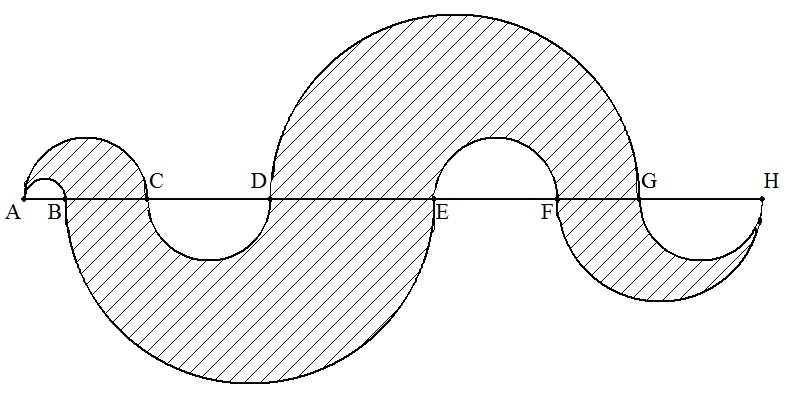
    (3)　線分AH上に8個の半円が図の様に配置されている。
    斜線部分の面積Sが次式で与えられることを証明せよ。
    S＝π（BC・AD+DE・BG+FG・EH）/4

  14. （中学生向け）
    三角形ABCは∠C＝90°の直角三角形で，ABの中点をMとする。
    BC，CA上にそれぞれ点P，Qを∠PMQ＝90°となるようにとる。
    このとき，次を証明せよ。
    (1)　△ABC∽△PQM
    (2)　PQ2＝BP2＋AQ2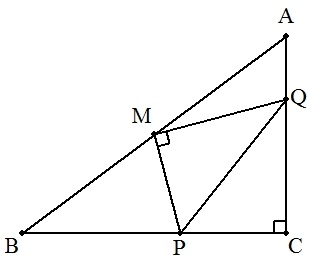
  15. （中学生向け）
    正方形ABCDの辺BC，CD上にそれぞれ点E，Fをとる。
    このとき，次を証明せよ。
    (1)　∠EAF=45°　⇒　BE+DF=EF
    (2)　BE+DF=EF　⇒　∠EAF=45°
    (3)　∠EAF=45°　⇒　∠AEB=∠AEF，∠AFD＝∠AFE
    (4)　∠AEB=∠AEF（または，∠AFD＝∠AFE）　⇒　∠EAF=45°
    (5)　∠EAF=45°　⇒　BE：CE＝CF：2DF
    (6)　BE：CE＝CF：2DF　⇒　∠EAF=45°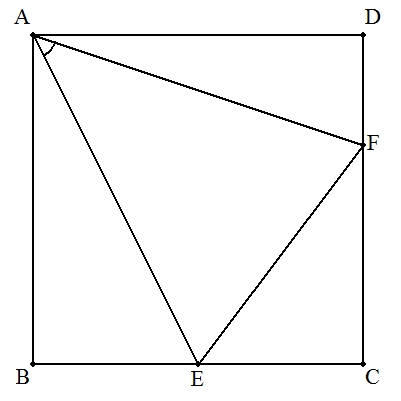
  16. （中学生向け）
    正方形ABCDの辺BC，CD上にそれぞれ点E，Fをとる。∠EAF=45°のとき，
    次の各場合について，正方形の一辺の長さを求めよ。
    (1)①BE＝a ，CF＝b のとき
    ②BE＝3，CF＝5のとき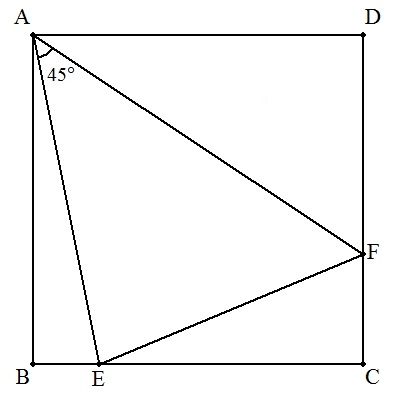
    (2)①BE＝a ，DF＝b のとき
    ②BE＝5，DF＝12のとき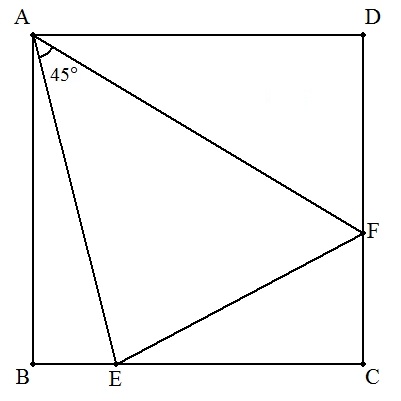
    (3)①BE＝a ，EF＝b のとき
    ②BE＝2，EF＝5のとき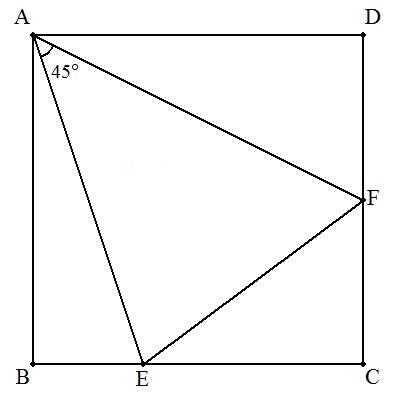
    (4)①EC＝a ，CF＝b のとき
    ②EC＝20，CF＝21のとき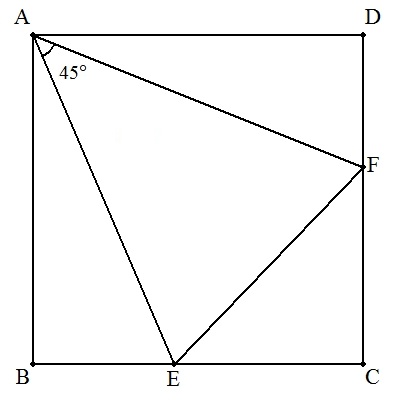
    (5)①AE＝a ，AF＝b のとき
    ②AE＝4√2 ，AF＝7のとき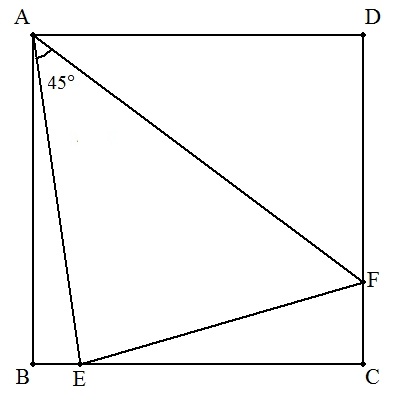
    (6)（難）BE＝4，AF＝35のとき
    (7)ABとFEの交点をP，ADとEFの交点をQとする。
    ①PE＝a ，QF＝b のとき
    ②PE＝2m2 ，QF＝n2のとき
    ③PE＝2 ，QF＝9 のとき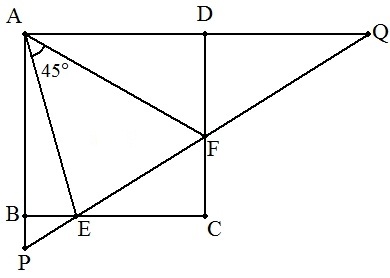
  17. （中学生向け）
    正方形ABCDの辺BC，CD上にそれぞれ点E，Fをとる。
    ∠EAF=45°，AB＝a ，BE＝b のとき，
    AF，EF，CFの長さをそれぞれ求めよ。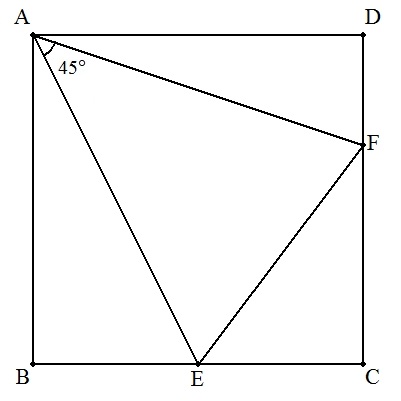
  18. （中学生向け）
    正方形ABCDの辺BC，CD上にそれぞれ点E，Fをとり，対角線BDとAF，AEとの
    交点をそれぞれG，Hとする。
    また，EFの中点Mから辺AB，ADに下ろした垂線の足をそれぞれI，Jとする。
    ∠EAF=45°のとき，次を証明せよ。
    (1)　対角線BDは△AEFの面積を二等分する。
    (2)　BH：HG：GD＝CF：FE：EC
    (3)　BH2+GD2=HG2
    (4)　△BEH，△AGH，△DAH，△AEF，△DFG，△BGAは全て相似である。
    (5)　BD，AE，IM およびBD，AF，JMはそれぞれ1点で交わる。
    (6)　長方形AIMJの面積は正方形ABCDの面積の半分に等しい。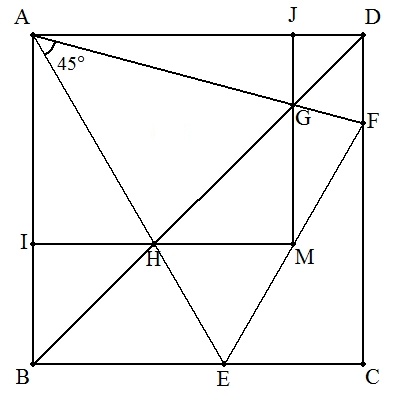
  19. （中学生向け）
    正方形ABCDの辺BC，CD上にそれぞれ点E，Fをとる。
    ∠EAF＝45°のとき，次の問いに答えよ。
    (1) 対角線BDとAF，AEとの交点をそれぞれG，Hとする。
    AB＝1，BE=a のとき，四角形EFGHの面積Sを求めよ。
    また，Sの最小値とそのときのaの値を求めよ。（高校生向け）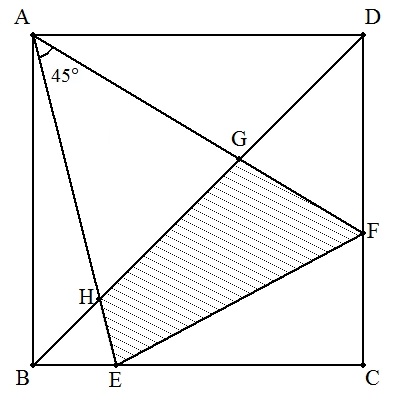
    (2) 対角線BDとAF，AEとの交点をそれぞれG，Hとし，
    BH＝a ，GD=b のとき，正方形の1辺の長さを求めよ。
    また，BH＝3，GD＝4のとき，正方形の1辺の長さを
    求めよ。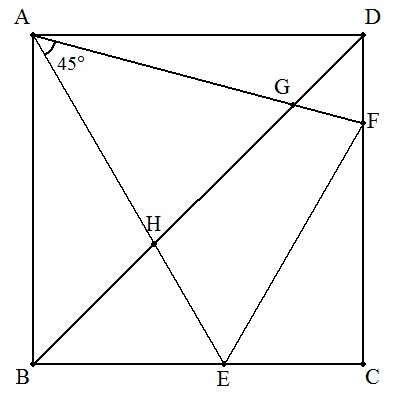
    (3) AB＝1，対角線BDとAEとの交点をH，EFの中点をM，
    △EMHが正三角形となるとき，BEの長さを求めよ。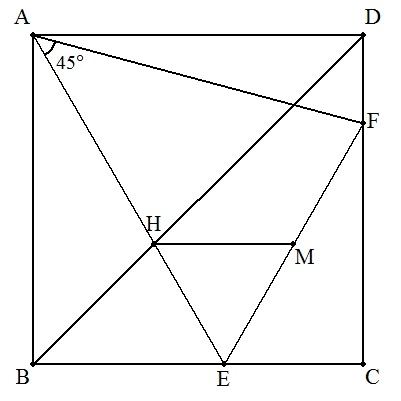
  20. （中学生向け）
    正方形ABCDの辺BCのCを越えた延長上に点Eを，
    辺CDのDを越えた延長上に点Fを，∠AEB＝∠AEF
    となるようにとるとき，∠EAFの大きさを求めよ。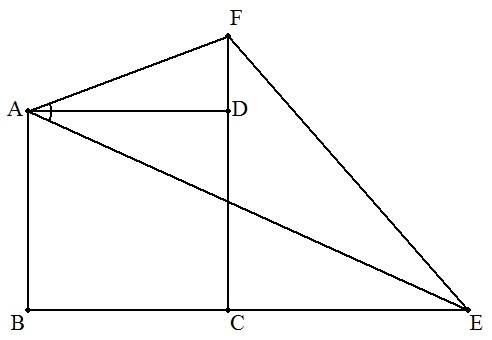
  21. （中学生向け）
    a，bを正の数とする。正方形ABCDの辺BC，CD上にそれぞれ点E，Fを，
    BE＝a(a+b)，EC=2b(a+b)，CF=a(a+2b)となるようにとるとき，
    ∠EAFの大きさを求めよ。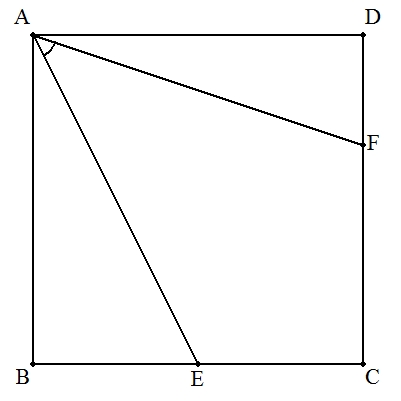

  22. 正三角形ABCの3辺BC，CA，AB上にそれぞれ点D，E，Fを BD：DC＝CE：EA＝AF：FB＝k：（1-k）となるようにとる。
    （ただし，1/2＜k＜1とする。）
    BE，CFの交点をP，CF，ADの交点をQ，AD，BEの交点をRとする。
    △PQR，△PBC，△QCA，△RABの内接円をそれぞれ I(r)，L(t)，M(t)，N(t)とおく。
    (1)r＝tのとき，kの値を求めよ。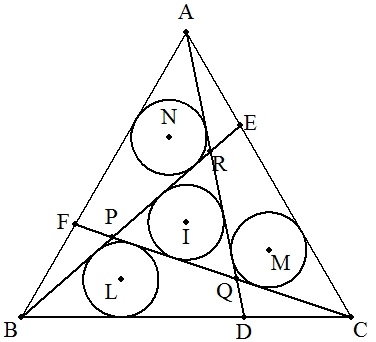
    (2)3円L，M，Nの面積和が円Iの面積に
    等しくなるとき，kの値を求めよ。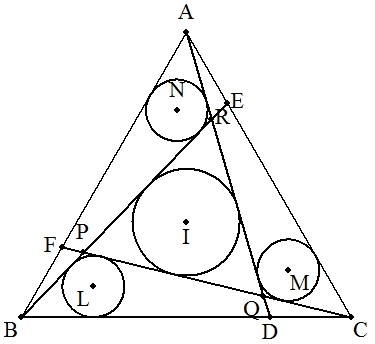
  23. （中学生向け）
    1辺の長さがaの正方形ABCDに，図のようにBCに接する2つの等円が内接している。
    この2円に頂点A，Dから接線を引き，その交点をEとする。
    (1)AEの長さを求めよ。
    (2)△AEDの内接円の半径rを求めよ。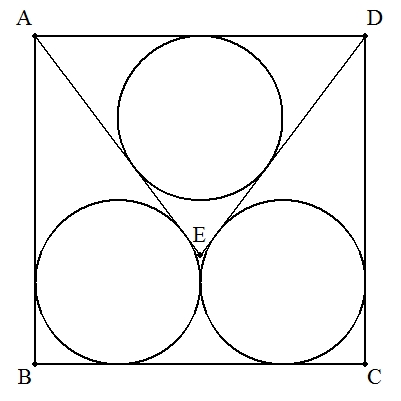

  24. 次を証明せよ。
    (1)円に正三角形ABCが内接し，劣弧AC上に点Pをとると，
    PA+PC=PB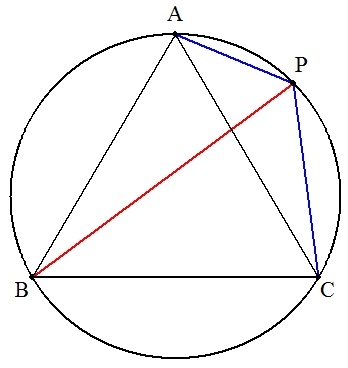
    (2)円に正五角形ABCDEが内接し，劣弧AE上に点Pをとると，
    PA+PC+PE=PB+PD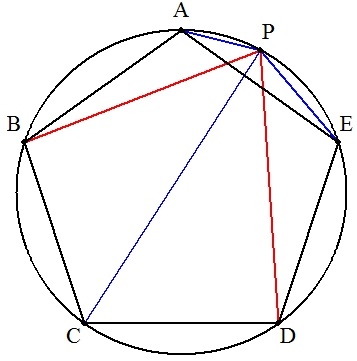
    (3)円に正七角形ABCDEFGが内接し，劣弧AG上に点Pをとると，
    PA+PC+PE+PG=PB+PD+PF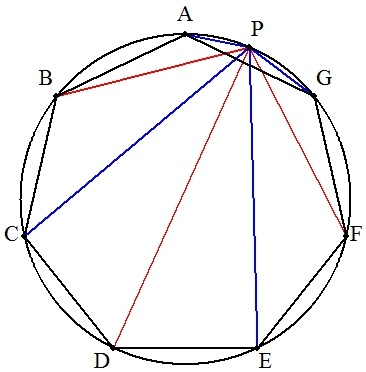

  25. 次の値を求めよ。
    (1)円に正方形ABCDが内接し，劣弧AD上に点Pをとるとき，
    (PA+PD)/(PB+PC)の値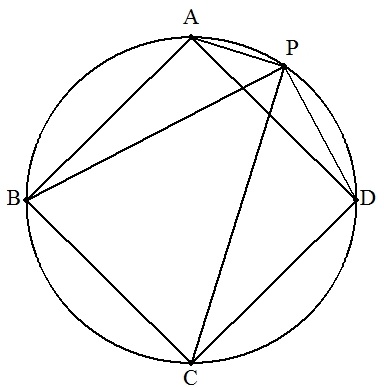
    (2)円に正六角形ABCDEFが内接し，劣弧AF上に点Pをとるとき，
    (PA+PC+PD+PF)/(PB+PC+PD+PE)の値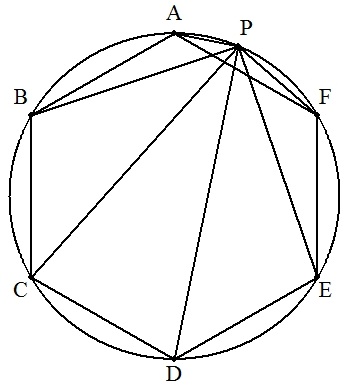

  26. 円に正（2n+1）角形A1A2･･･A2n+1が内接し，劣弧A1A2n+1上に点Pをとると
    PA1+PA3+･･･+PA2n+1=PA2+PA4+･･･+PA2n
    となることを証明せよ。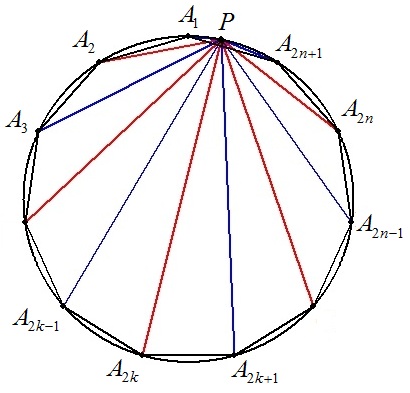

  27. 三角形ABCの辺BC上に点Dを，
    △ABDと△ACDのそれぞれの内接円の
    半径が等しくなるようにとる。
    このとき，
    (1)　BDを求めよ。
    (2)　ADを求めよ。
    (3)　△ABDの内接円の半径を求めよ。
    (4)　a＝4，b＝3，c＝2のとき，(1)～(3)の値を求めよ。
    (5)　a，b，cを正の整数とする。(1)～(3)の値が整数になる例を求めよ。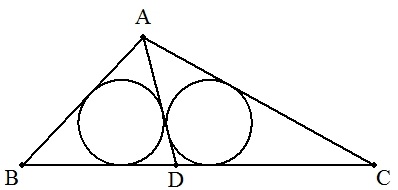

  28. 1辺の長さがaの正方形ABCDの内部に4点P，Q，R，Sをとり，図のように4個の合同な直角三角形ABP，BCQ，CDR，DASをつくる。
    これらの直角三角形の内接円の半径をr1，正方形PQRSの内接円の半径をr2とする。
    (1)　r1，r2の関係式を求めよ。
    (2)　r1＝r2のとき，r1を求めよ。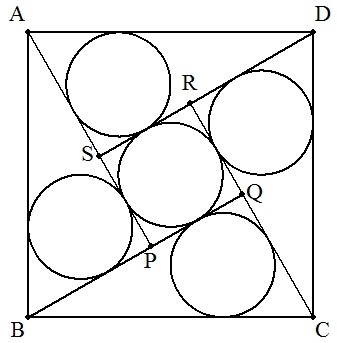
    (3)　4個の直角三角形に内接する円の面積の和が正方形PQRSの
    内接円の面積に等しくなるとき，r1，r2を求めよ。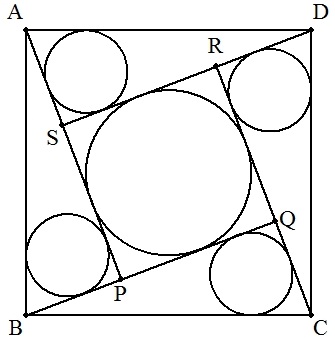

  29. 1辺の長さがaの正五角形ABCDEの内部に5点P，Q，R，S，Tをとり，
    図のように5個の合同な三角形ABP，BCQ，CDR，DES，EATをつくる。
    これらの三角形の内接円の半径をr1，正五角形PQRSTの内接円の
    半径をr2とする。
    (1)　r1＝r2のとき，r1を求めよ。
    (2)　5個の三角形に内接する円の面積の和が正五角形PQRSTの
    　内接円の面積に等しくなるとき，r1，r2を求めよ。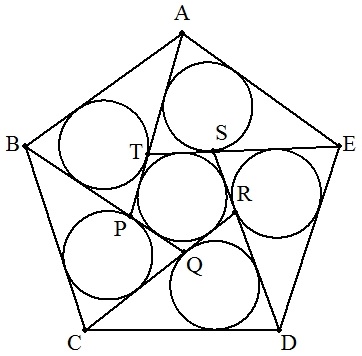

  30. 1辺の長さがaの正六角形ABCDEFの内部に6点P，Q，R，S，T，Uをとり，
    図のように6個の合同な三角形ABP，BCQ，CDR，DES，EFT，FAUをつくる。
    これらの三角形の内接円の半径をr1，正六角形PQRSTUの内接円の
    半径をr2とする。
    (1)　r1＝r2のとき，r1を求めよ。
    (2)　6個の三角形に内接する円の面積の和が正六角形PQRSTUの
    　内接円の面積に等しくなるとき，r1，r2を求めよ。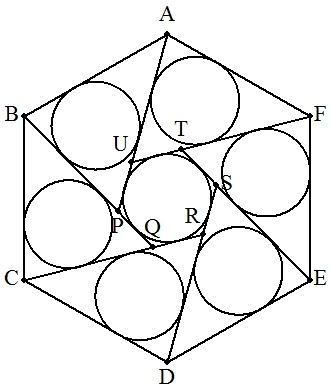

  31. 1辺の長さがaの正三角形ABCの内部に3点P，Q，Rをとり，図のように3個の合同な三角形ABP，BCQ，CARをつくる。
    これらの三角形の内接円の半径をr1，正三角形PQRの内接円の半径をr2とする。
    (1)　r1＝r2のとき，r1を求めよ。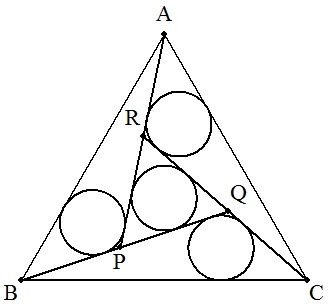
    (2)　3個の三角形に内接する円の面積の和が正三角形PQRの
    　内接円の面積に等しくなるとき，r1，r2を求めよ。

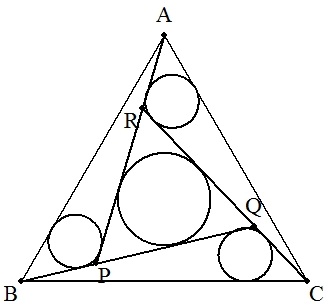  32. 幅がaの紙で右の図のように結びを作る。
    (1)　このときできる正五角形の1辺の長さを求めよ。
    (2)　図の点線のところで切り落とし，残った部分をほどいて広げたとき，紙の長さを求めよ。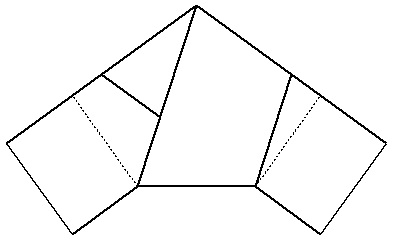
  33. （中学生向け）
    (1)　円の直径ABの上側の半円周を5等分し，下側の半円周を6等分する。
    　図のように，分点を結んだ弦CHとDEの交角（劣角）を求めよ。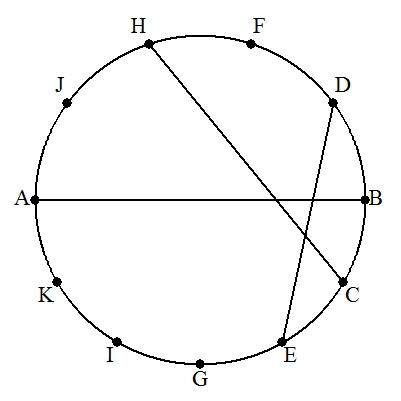
    (2)　2点A，Bは円の直径の両端である。
    　直径ABの上側の半円周をm等分し，その分点を図のようにCm,1，Cm,2，･･･，Cm,m-1とする。
    　同様に，直径ABの下側の半円周をn等分し，その分点を図のようにDn,1，Dn,2，･･･，Dn,n-1とする。
    　2つの弦Cm,iDn,jとCm,kDn,lが円内で交わるとき，2つの弦のなす角を求めよ。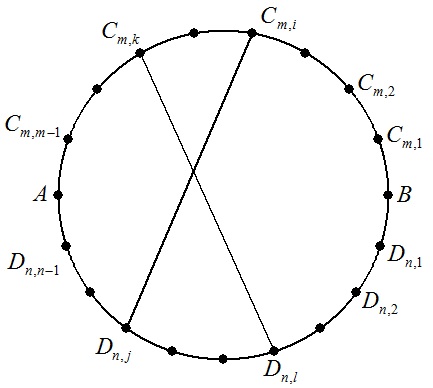
  34. （小中学生向け）
    四角形ABCDにおいて，AB＝AD，BC＋CD＝6，
    ∠DAB＝90°，∠ABC＝60°，∠BCD＝90°のとき，
    四角形ABCDの面積を求めなさい。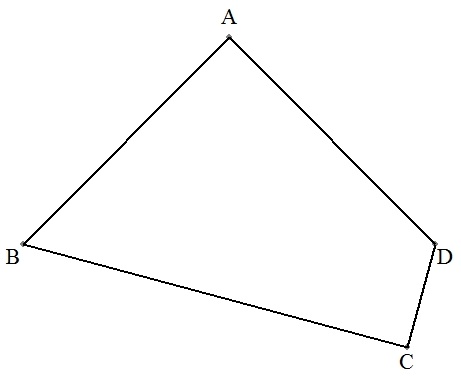
  35. （中学生向け）
    AD∥BCの台形ABCDについて，対角線の交点をE，
    AB＝AC，BC＝BD，∠BAC＝90°であるとき，
    CD＝CEを証明せよ。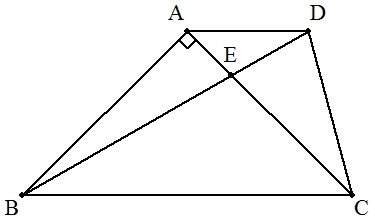
  36. （中学生向け）
    △ABCにおいて，∠B＝2∠Cのとき，
    ∠Bの2等分線にAから下ろした垂線の足をDとすると，
    BD＝AC/2となることを証明せよ。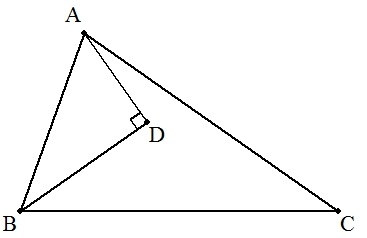
  37. （中学生向け）
    右図の正方形ABCDについて，
    ∠EAB＝27°，∠FAD＝18°，
    MはEFの中点，△MGHは直角三角形，
    ∠MHF＝81°である。
    ∠MGH＝xの大きさを求めよ。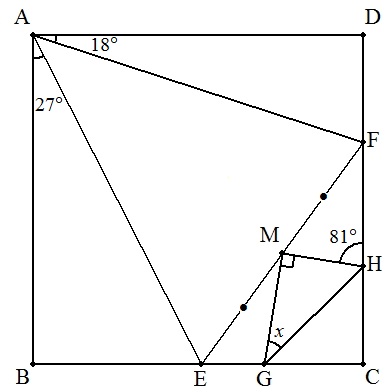

  38. (1)　△ABCにおいて，B＝2Cのとき，
    b2をa，cで表せ。
    また，a＝5，c＝4のとき，bを求めよ。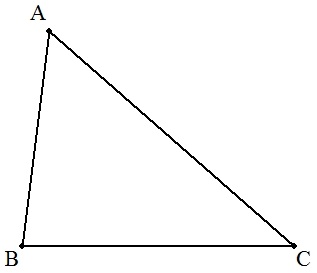
    (2)　△ABCにおいて，B＝3Cのとき，
    a2をb，cで表せ。
    また，b＝48，c＝27のとき，aを求めよ。
    (3)　△ABCにおいて，B＝4Cのとき，
    b2をa，cで表せ。
    また，a＝11，c＝4のとき，bを求めよ。
    (4)　△ABCにおいて，B＝5Cのとき，
    a2をb，cで表せ。
    また，b＝11，c＝4のとき，aを求めよ。
    (5)　△ABCにおいて，B＝6C，a＝7，c＝8のとき，
    bを求めよ。
    (6)　△ABCにおいて，B＝7C，b＝13，c＝8のとき，
    aを求めよ。
  39. （小中学生向き）
    右の四角形ABCDについて，BC＝CDのとき，∠BCAの大きさを求めよ。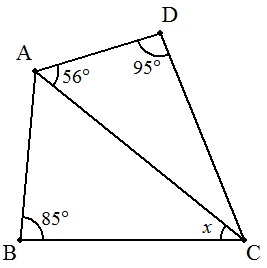
  40. （中学生向き）
    点Aから円Oに接線AB，ACを引く。
    このとき，三角形ABCの内接円の中心は
    円Oの周上にあることを証明せよ。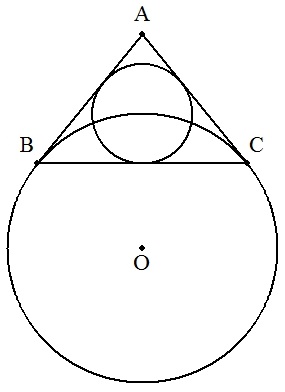
  41. （中学生向き）
    △ABCは直角三角形で，AB＝5，BC＝4，CA＝3，
    ∠C＝90°である。
    AB上に点Dを，BD＝BCとなるようにとり，
    BC上に点Eを，△DBE＝△ABC/2となるようにとる。
    このとき，DEを求めよ。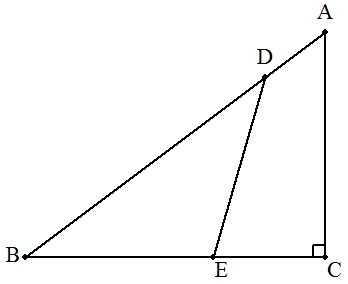

  42. △ABCは直角三角形で，∠C＝90°である。
    AB上に点Dを，AD＝BCとなるようにとり，
    AC上に点Eを，△ADE＝△ABC/2となるようにとる。
    (1)　点Eの取り方を説明せよ。
    (2)　BC=a，CA=bのとき，DEを求めよ。
    (3)　BC=3，CA=4のとき，DEを求めよ。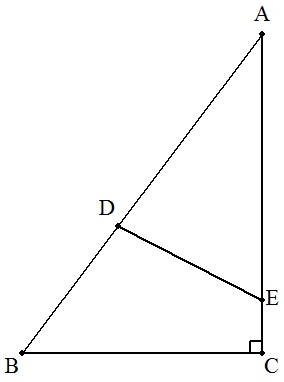

  43. △ABCのBC上に動点Pをとり，
    ACの中点をM，BMとAPの交点をQ，
    頂点BからACに下ろした垂線BHとAPの交点をR，
    ∠Bの2等分線とAC，APの交点をそれぞれD，Sとする。
    次の条件を満たすBPの長さを求めよ。
    ただし，BC＝a，CA＝b，AB＝cとする。
    (1)　△AMQ＝△BPQ
    (2)　△AHR＝△BPR
    (3)　△ADS＝△BPS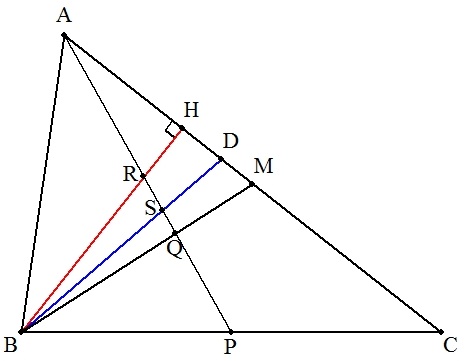

  44. 2直線l，mは平行で，点Aは直線lの上側に，点Bは直線mの下側にとる。
    点Cを直線l上にとり，Cから直線mに下ろした垂線の足をDとする。
    このとき，AC＋CD＋DBが最小になるようなAC，CD，DBを図示せよ。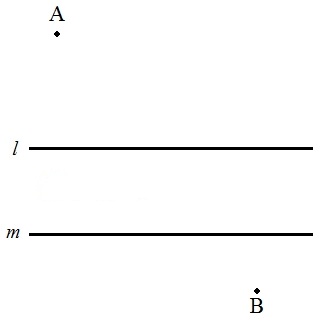

  45. AB=5，BC=8，CA=7の△ABCの辺BCの中点をH，△ABC内に点Pを，
    PH⊥BC，PH＝1となるようにとる。
    CA上に点Dを，AB上に点Eを，△PDEの周の長さが最小になるよ
    うにそれぞれとる。
    このとき，△PDEの面積を求めよ。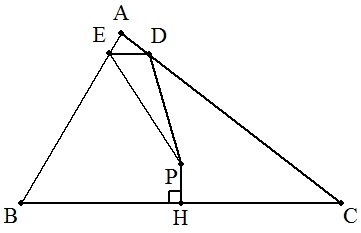
  46. （中学生向け）
    交わらない2円O1，O2の共通外接線をL1，L2，
    それらの接点を図のようにA，B，C，Dとする。
    1つの共通内接線をL3とし，接点を図のように
    E，Fとする。L3とL1，L2との交点をそれぞれ
    P，Qとする。EPの中点をM，BQの中点をNと
    する。∠PBN＝66°，∠PQN＝50°のとき，
    ∠BNMの大きさを求めよ。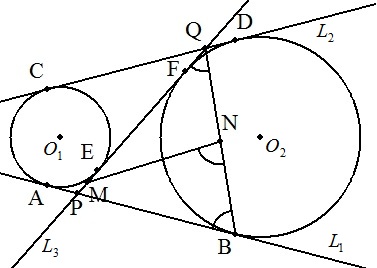
  47. （中学生向け）
    (1) △ABCと△BDEは合同な二等辺三角形で，
    頂角は20°である。
    このとき，次の角の大きさを求めよ。
    ①　∠ADE
    ②　∠CED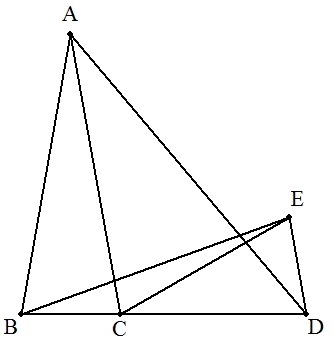
    (2) △ABCは頂角20°の二等辺三角形，
    △CDEは頂角40°の二等辺三角形，
    △CDAはCD＝CAの二等辺三角形である。
    このとき，次の角の大きさを求めよ。
    ①　∠ADE
    ②　∠EBD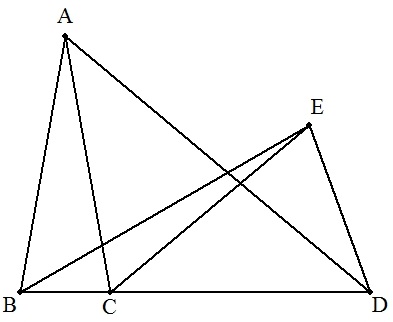
  48. （中学生向け）
    △ABCにおいて，2∠B＝∠Cとする。
    BCの延長上に点DをAB＝CDとなるように
    とると，∠ADC＝30°であった。
    ∠ABCの大きさを求めよ。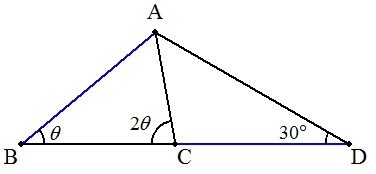

  49. a=8，b=7，c=5の△ABC内に点Pを，
    ∠APB＝∠BPC＝∠CPAとなるようにとる。
    AP，BP，CPを求めよ。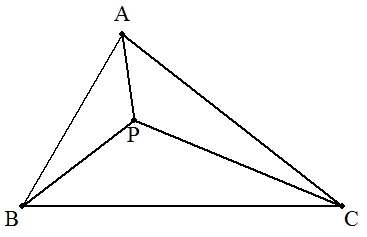

  50. 下図の線分ABを直径とする半円について，BAの延長上に点Oをとり，
    Oから半円への接線をOC0，C0からABへの垂線をC0D0，AB上に点D1を
    OC0⊥C0D1となるようにとり，半円周上に点C1をAB⊥D1C1となるようにとる。
    このときD1は半円の中心となる。次に，AB上に点D2をOC1⊥C1D2となるようにとり，
    半円周上に点C2をAB⊥D2C2となるようにとる。以下同様に，D3，C3，D4，C4，･･･
    と点をとっていく。すなわち，OCn⊥CnDn+1，AB⊥Dn+1Cn+1である。
    また，線分OCnと弧ABとの交点をC-n，点C-nからABへの垂線をC-nD-nとする。

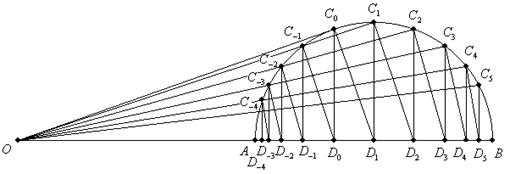
    今，OA＝a，OB＝b（0＜a≦b）とする。
    ただし，a＝bのとき，点A，B，Cn，Dn（nは整数）は一致するものとする。
    nを整数として，次の長さをa，bを用いて表せ。
    (1)　ODn
    (2)　CnDn
    (3)　OCn