■趣味の数学問題集・Ａ問題
  1. （中学生向け）
    AB＝ACの二等辺三角形ABCについて，辺
    AB，ACを一辺とする正三角形ABD，ACEを
    △ABCと重ならないようにつくる。
    さらに，点FをDA=DF=EFとなるようにとる。
    このとき，次を証明せよ。
    (1)　AB＜BCのとき，△FBCは正三角形となる。（上図）
    (2)　AB＞BCのとき，△FBCは正三角形となる。（下図）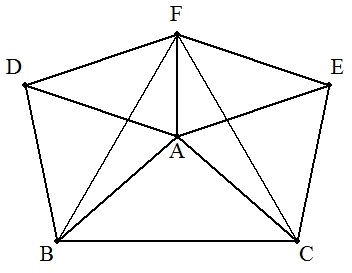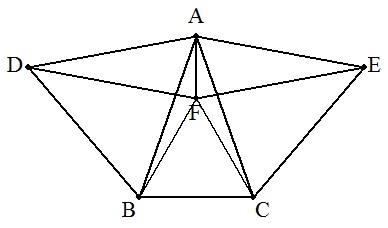
  2. （中学生向け）
    面積がSである四角形ABCDについて，
    BAとCDの交点をE，ADとBCの交点をFとする。
    対角線BD，ACの中点をそれぞれL，Mとする。
    (1)　四角形ABMDの面積をSを用いて表せ。
    (2)　四角形ALMDの面積をSを用いて表せ。
    (3)　△LMEの面積をSを用いて表せ。
    (4)　△LMFの面積をSを用いて表せ。
    (5)　EFの中点をNとすると，3点L，M，Nは
    　一直線上にあることを証明せよ。
  3. （中学生向け）
    四角形ABCDは円に内接し，AB=4,BC=6,CD=5,DA=3である。
    対角線の交点をE，DAとCBの交点をF，BAとCDの交点をG，
    FGとCAの交点をHとする。 このとき，FH：HGを求めよ。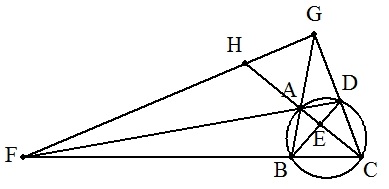

  4. 一辺の長さが1の正方形ABCD内に辺BCを
    一辺とする正三角形EBCを描く。
    直線AEとCDとの交点をF，辺BC上に点Gを
    △AFGが正三角形になるようにとる。
    AGとBEとの交点をH，CEとFGとの交点を
    Iとする。
    (1)　△ABHの内接円rの半径を求めよ。
    (2)　△HBG，△EFI，△HEI，△HAE，△GCIの
    　内接円の半径をそれぞれrを用いて表せ。
    (3)　△CFI，△AFD，△GHIの内接円の半径
    　をそれぞれ求めよ。
    (4)　△GHI/△EBC，△EHI/△AGFの値を
    　それぞれ求めよ。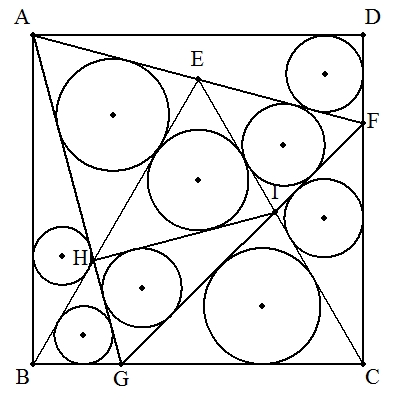　
  5. （中学生向け）
    正方形ABCDの辺CDの中点を中心
    とする半円Oに接線BEを引く。
    △ABEの内接円をPとする。
    この2円の共通外接線をFGとし，
    FGとBEの交点をHとする。
    △HBGと△HFBの内接円をQ，R，
    2円P，Qの共通外接線をMNとする。
    MNとFG，BEとの交点をそれぞれI，
    Jとし，△JEM，△JIH，△GINの
    内接円をそれぞれS，T，Uとする。
    円Oの半径をrとするとき，円P，Q，
    R，S，T，Uの半径をrを用いて表せ。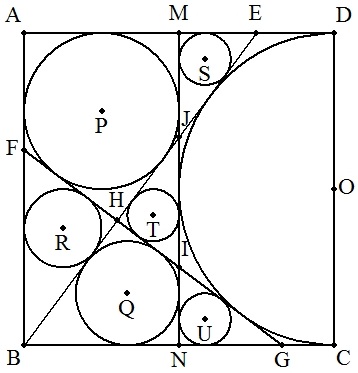
  6. （中学生向け）
    正方形ABCDの辺CDの中点をOとし，Oを中心，
    半径OCの半円を正方形内につくる。その半円
    に点Bから接線を引き，辺ADとの交点をEとす
    る。△ABEの内接円の中心をPとし，半円Oと
    円Pの共通外接線と2辺AB，BCとの交点をそれ
    ぞれF，Gとする。FGとBE，HEとOP，BPとFGの
    交点を順にH，I，Jとする。このとき，四角形
    HIPJは円に内接することを証明せよ。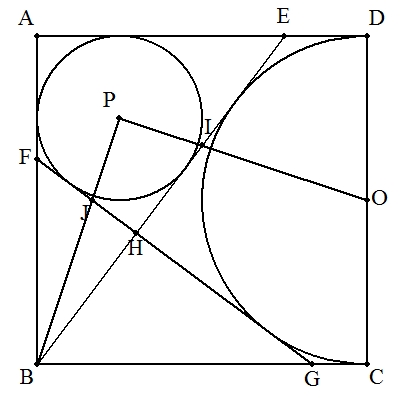
  7. （中学生向け）
    正方形ABCDの辺BC，CD上にそれぞれ点E，Fを，
    ∠AEB＝∠AEFとなるようにとり，対角線BDと
    AE，AFとの交点をそれぞれG，Hとする。
    BE＝3，DF＝2のとき，BG：GH：HDを求めよ。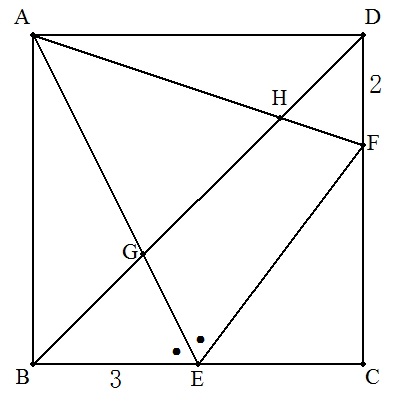
  8. （中学生向け）
    ∠A＝90°の直角三角形ABCの点AからBCに
    下ろした垂線の足をDとする。△ABD，△ACDの
    内接円をそれぞれP，Qとし，円P，Qの共通外
    接線とAB，ACとの交点をそれぞれE，Fとする。
    また，ADとEFの交点をGとする。
    このとき，△AFE∽△ABCを証明せよ。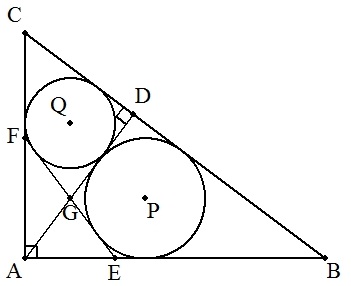

  9. BC＝a，CA＝b，AB＝cの△ABCがある。
    辺BC上に点Dを，辺CA上に点Eをとり，
    頂点Cを線分DEで折り返し，辺AB上の点
    Fに重ねる。∠AFE＝∠Cのとき，
    (1)　CE：EAを求めよ。（中学生向け）
    (2)　AF：FBを求めよ。（中学生向け）
    (3)　BD：DCを求めよ。
    (4)　DEを求めよ。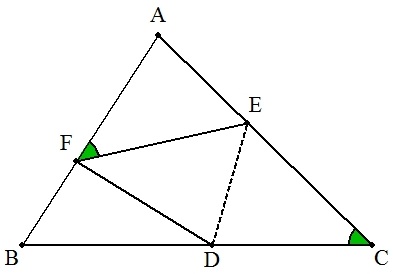
  10. （中学生向け）
    正三角形ABCの外接円の劣弧AC上に点D
    を弧AD：弧DC＝m：nとなるようにとる。
    次に，BD上に点EをDA/2＝DEとなるよう
    にとり，BCの中点をFとする。
    (1)　m＝1，n＝3のとき，∠EFCの大きさ
    　を求めよ。
    (2)　∠EFC＝57°となるとき，m，nの値
    　を求めよ。ただし，m，nは最小の正の
    　整数とする。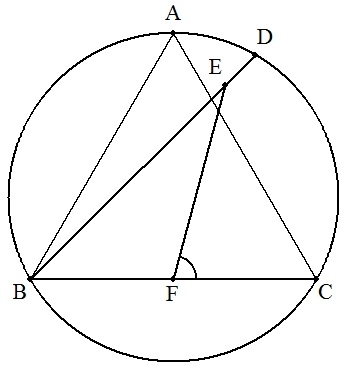
  11. （中学生向け）
    正三角形ABCの外接円の劣弧AC上に点Dを
    とる。BD上に点Eを，AD/2＝DEとなるように
    とり，BCの中点をFとする。このとき，
    ∠BEF＝30°となることを証明せよ。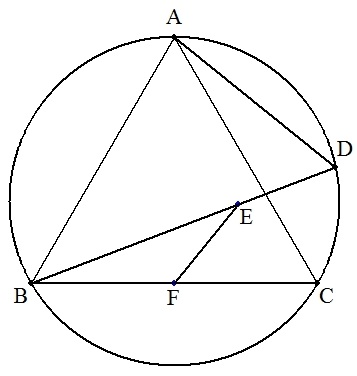
  12. （中学生向け）
    半径が2である扇形OABについて，弧ABの
    3等分点をAに近い方からC，Dとする。
    2点B，CからOAに下ろした垂線の足を，
    それぞれE，Fとする。
    また，BCとODの交点をG，BEとOCの交点
    をHとする。
    いま，OE＝1とし，OF＝x，CF＝yとおく。
    (1)　∠CBEを求めよ。
    (2)　CH×CO＝CB2を証明せよ。
    (3)　△HOE∽△COFより，y2をxで表せ。
    (4)　xの満たす方程式を求めよ。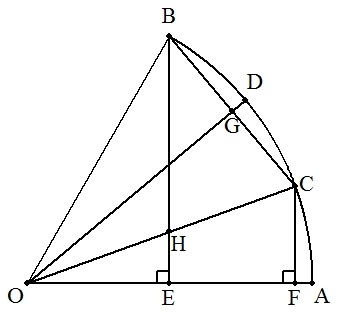
  13. （中学生向け）
    正方形ABCDの2辺BC，CD上に，それぞれ点E，Fを，∠EAF＝45°となるようにとる。
    次の各場合に，正方形ABCDの面積およびBEの長さを求めよ。
    (1)△AEF＝5，△BEA＝3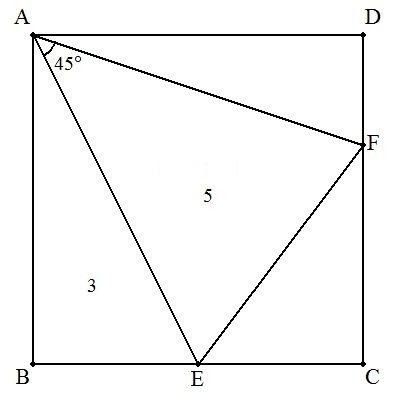
    (2)△AEF＝25，△CFE＝6，BE>DF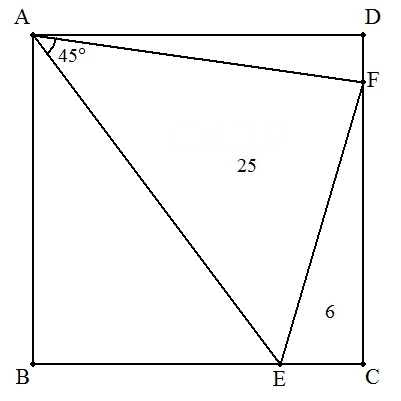
    (3)△BEA＝5，△CFE＝3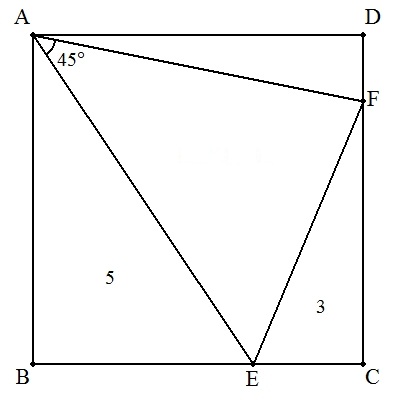
    (4)△BEA＝5，△DAF＝12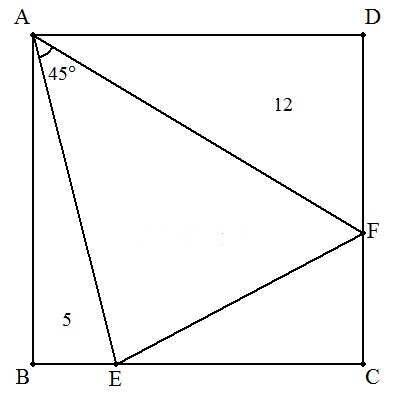
  14. （中学生向け）
    正方形ABCDの2辺BC，CD上に，それぞれ点E，Fを，
    ∠EAF＝45°となるようにとる。
    正方形の面積をS，△AEF，△BEA，△CFE，△DAFの
    面積をそれぞれa，b，c，dとおく。
    (1)　a，bの値から，SおよびBEの長さを求めよ。
    (2)　a，cの値から，SおよびBEの長さを求めよ。
    (3)　b，cの値から，SおよびBEの長さを求めよ。
    (4)　b，dの値から，SおよびBEの長さを求めよ。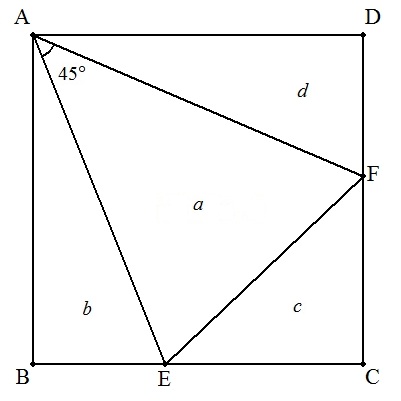

  15. 正方形ABCDの2辺BC，CD上に，それぞれ点E，Fを，
    ∠EAF＝45°となるようにとる。
    次の各場合について，ABの長さを求めよ。
    (1)BE=3，△AFD＝6のとき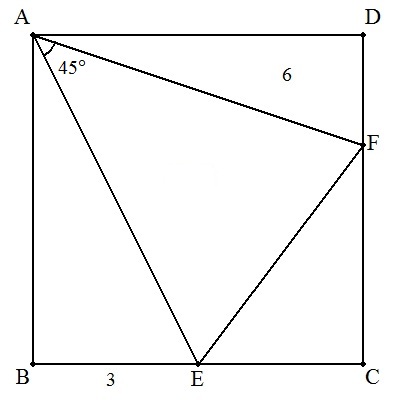
    (2)BE=√5，△AEF＝34のとき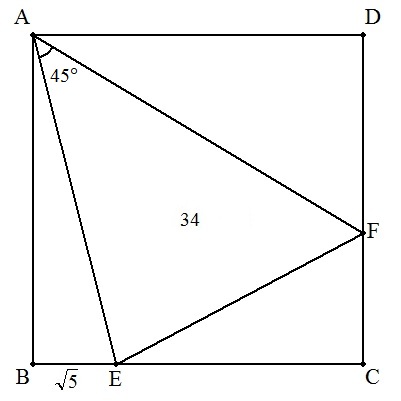
    (3)BE=a，△CFE＝sのとき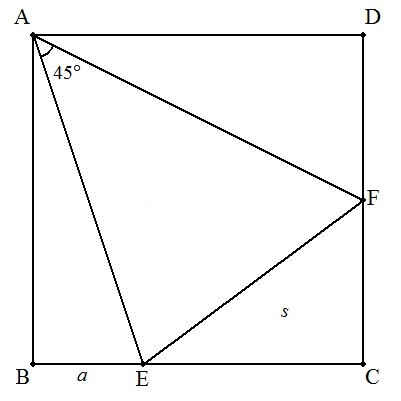

  16. 正方形ABCDの2辺BC，CD上に，それぞれ点E，Fをとる。
    次の各場合について，∠xの大きさを求めよ。
    (1)∠AEB＝∠AEFのとき，
    ∠EAF＝x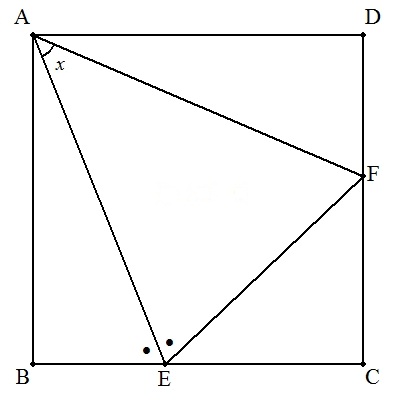
    (2)∠BAE＝27°，
    ∠DAF＝18°のとき，
    ∠AFE＝x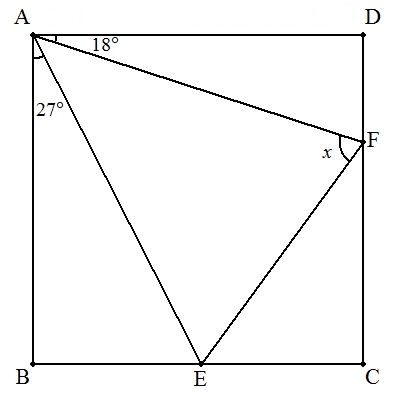
    (3)∠AEB＝∠AEF，
    ∠FEC＝18°のとき，
    ∠DAF＝x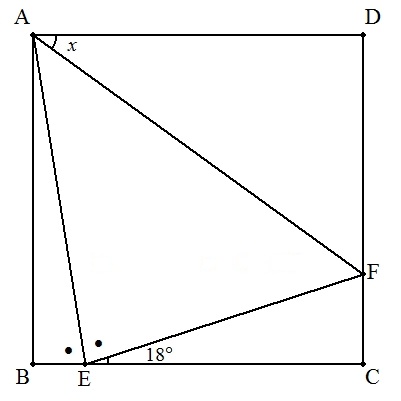
    (4)∠AEB＝∠AEF，
    ∠DAF＝∠FECのとき，
    ∠DAF＝x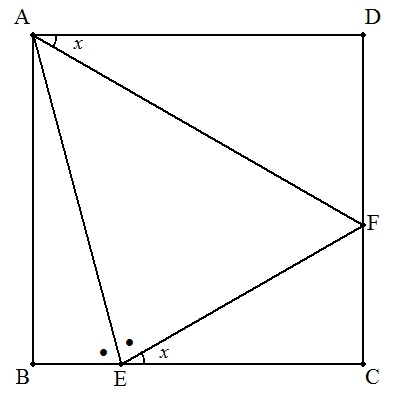

  17. ABを直径とする半円周の4等分点をBに
    近い方から順に，C，D，Eとする。
    △BCD，△BDE，△BEAの内接円を，順に
    O1（r1），O2（r2），O3（r3）とする。
    AB＝2rとおくとき，r1，r2，r3を求めよ。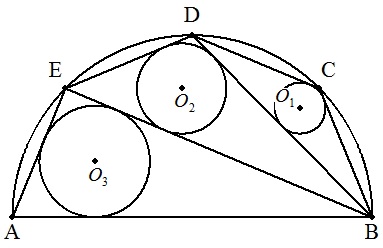

  18. C＝90°の直角三角形ABCに，図のようにn×n個の半径r
    の等円が内接している。
    ただし，1行目のn個の円の中心を通る直線はBCに平行で，
    1列目のn個の円の中心を通る直線はACに平行である。
    BC＝a，CA＝bのとき，rをa，b，nを用いて表せ。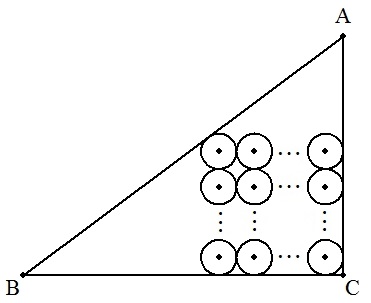

  19. 1から9までの数字を順に使い，例にならって2014を作れ。
    （例1）2012＝1234－5－6＋789
    （例2）2013＝1＋2345－6×7×8＋√9

  20. （中学生向け）
    正三角形ABC内の点Pから3辺BC，CA，ABに下ろした
    垂線の足を順にD，E，Fとする。
    次を証明せよ。
    (1)　AF2+BD2+CE2＝BF2+CD2+AE2
    (2)　AP：EF＝BP：FD＝CP：DE＝2：√3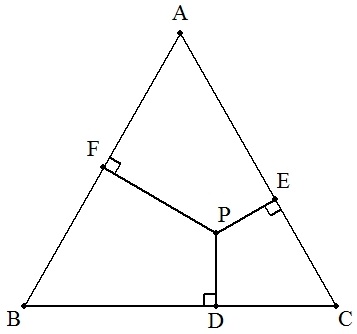

  21. △ABCの辺BCに接するn個の連結する等円
    O1，O2，･･･，Onのうち，O1は辺ABにも接し，
    Onは辺CAにも接している。このn個の等円の
    半径を，△ABCの内接円の半径rとBC＝a，n
    を用いて表せ。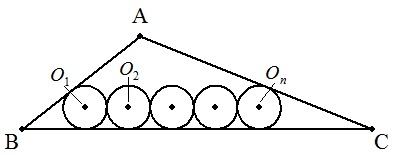

  22. 正方形ABCDの辺BCの延長上に点Eをとる。
    DEを一辺とする正方形DEFGを図のように
    つくる。点FからBCの延長上に垂線を下ろ
    し，その足をHとする。FHを一辺とする
    正方形FHIJを図のようにつくる。さらに，
    GJを一辺とする正方形GJKL，AGを一辺と
    する正方形AGMNを図のようにつくる。
    BC＝a，CE＝bのとき，次の問いに答えよ。
    (1)　正方形DEFG，正方形FHIJ，正方形
    　GJKL，正方形AGMNの面積を求めよ。
    (2)　△GLMの面積を求めよ。
    (3)　LMの長さを求めよ。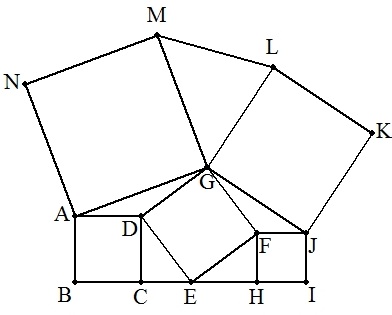

  23. 長方形ABCDの2辺BC，CD上にそれぞれ点E，Fをとる。
    (1)　△ABE＝4，△ECF＝6，△FDA＝3のとき，△AEFの
    　面積を求めよ。
    (2)　△ABE＝l，△ECF＝m，△FDA＝nのとき，△AEFの
    　面積をl，m，nを用いて表せ。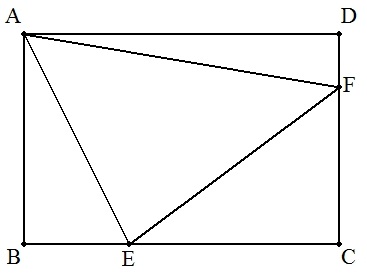

  24. 正方形ABCDの辺BC上に点Eを，辺CD上に
    点Fをとる。
    △ABE＝2，△ECF＝2，△FDA＝3のとき，
    (1)　正方形の1辺の長さを求めよ。
    (2)　△AEFの内接円の半径を求めよ。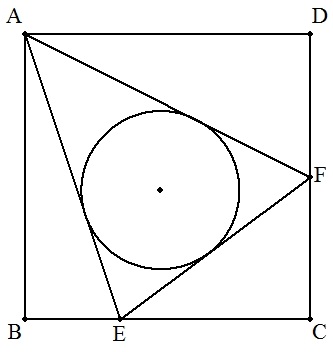

  25. △ABCの頂点A，B，Cから対辺BC，CA，ABに下ろした
    垂線の足をそれぞれD，E，Fとする。
    AD＝h，BE＝i，CF＝jのとき，
    (1)　△ABCの内接円の半径を求めよ。
    (2)　△ABCの面積を求めよ。
    (3)　h＝8，i＝9，j＝10のとき，△ABCの内接円の
    　半径と面積をそれぞれ求めよ。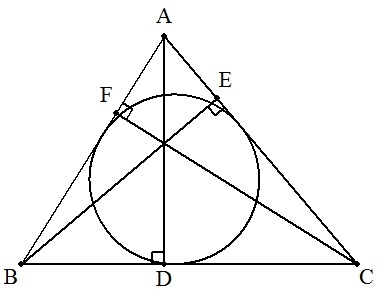
  26. （中学生向け）
    △ABCの3中線AD，BE，CFを3辺とする三角形の面積は，
    △ABCの面積の4分の3であることを証明せよ。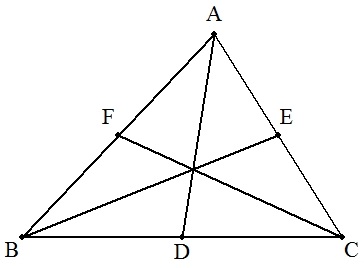
  27. （中学生向け）
    (1)　右の図で，△AFG＝6，△BFG＝4，△BDG＝5のとき，
    　△ABCの面積を求めよ。
    (2)　一般に，△AFG＝S1，△BFG＝S2，△BDG＝S3のとき，
    　△ABCの面積を求めよ。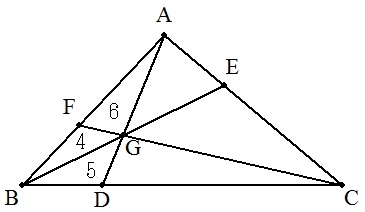
  28. （中学生向け）
    AB＝a，AD＝b（a＜b＜3a）である長方形ABCDに
    図のように3個の等円P，Q，Rが配置されている。
    (1)　円の半径rを求めよ。
    (2)　a，bが正の整数で，rが有理数となる例を1つ
    　求めよ。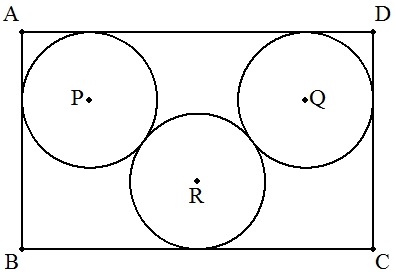
  29. （中学生向け）
    半径rの円Oに，5個の1辺の長さがaの正方形が
    図のようにOを中心に対称に配置されている。
    aをrを用いて表せ。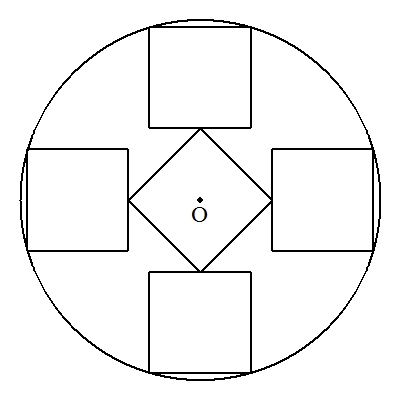
  30. （中学生向け）
    半径rの円Oの周上に，図のように6点
    A，B，C，D，E，Fをとり，AB，EFの
    交点をG，EF，CDの交点をH，CD，ABの
    交点をIとする。
    このとき，円内にできる4個の三角形が
    すべて合同な正三角形になるとき，
    正三角形の1辺の長さaをrを用いて表せ。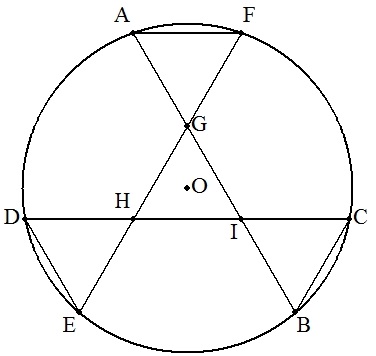

  31. 半径rの円Oに，6個の1辺の長さがaである正五角形が
    図のように配置されている。aをrを用いて表せ。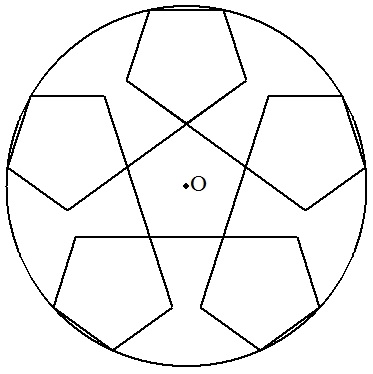

  32. 図のように，円Oに正六角形ABCDEF
    の頂点A，Fが内接している。
    この正六角形を，Oを中心に60°，
    120°，180°，240°，300°回転さ
    せ，合計6個の正六角形を円の内側
    につくる。（図では60°回転させた
    ものが表示されている。）
    次に，CDの中点をPとし，この点をO
    を中心に60°，120°，180°，240°，
    300°回転させ，点Q，R，S，T，Uを
    とり，正六角形PQRSTUをつくる。
    正六角形ABCDEFとPQRSTUが合同
    になるとき，正六角形の1辺aを，円O
    の半径rを用いて表せ。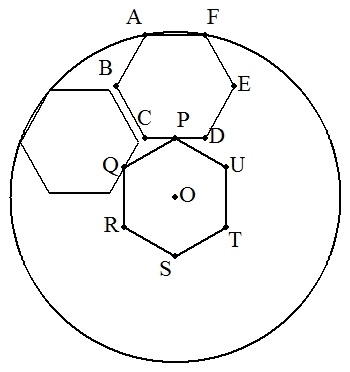

  33. 図のように，円Oに正七角形ABCDEFG
    の頂点A，Gが内接している。
    いま，2π/7＝θとおく。
    この正七角形を，Oを中心にθ，2θ，
    3θ，4θ，5θ，6θ回転させ，合計
    7個の正七角形を円の内側につくる。
    （図ではθ回転させたものを表示）
    次に，点Dを，Oを中心にθ，2θ，3θ，
    4θ，5θ，6θ回転させ，点H，I，J，K，
    L，Mをとり，正七角形DHIJKLMをつく
    る。正七角形ABCDEFGとDHIJKLM
    が合同になるとき，正七角形の1辺a
    を，円Oの半径rを用いて表せ。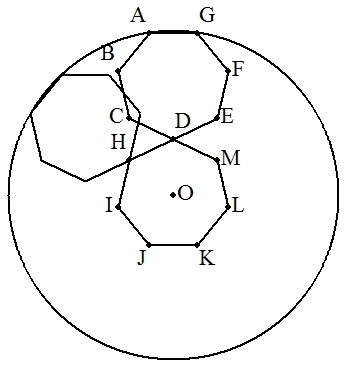

  34. (1)図のように，長方形ABCD内に3個の等円が配置されている。
    このとき，AD/ABを求めよ。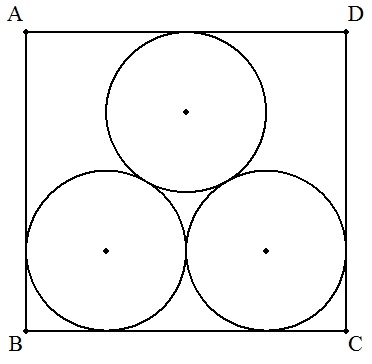
    (2)図のように，長方形ABCD内に7個の等円が配置されている。
    このとき，AD/ABを求めよ。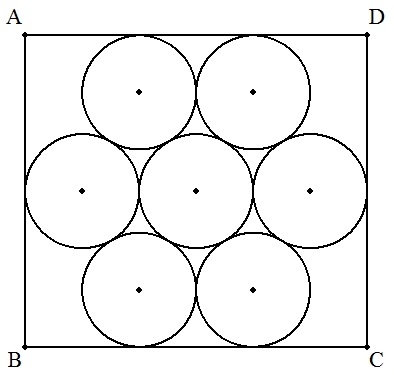
    (3)図のように，長方形ABCD内に5個の等円が配置されている。
    ただし，5個の円の中心は正五角形をつくる。
    このとき，AD/ABを求めよ。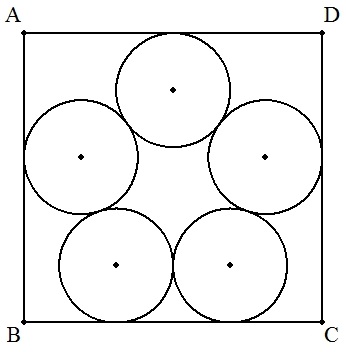

  35. 半円O内に図のように3個の正方形が配置されている。
    正方形ABCDは，辺BCが直径上にあり，点Aは円周上にある。
    正方形DEFGは，点Eが直径上にあり，点Gは円周上にある。
    正方形FHIJは，辺HIが直径上にあり，点Jは円周上にある。
    3個の正方形の辺の長さをCD＝a，DE＝b，FH＝c（a＜c）
    とおくとき，それらを半円の半径rを用いて表せ。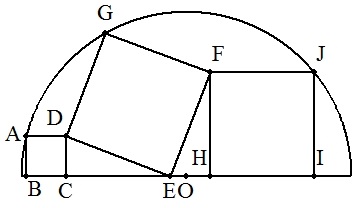

  36. 正三角形ABCの外接円の劣弧AC上に点Dをとる。
    点AからBDに下ろした垂線の足をE，BCの中点を
    Fとする。
    AB＝7，AD＝5のとき，EFの長さを求めよ。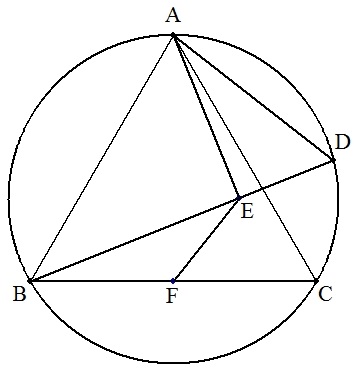

  37. xについての2次方程式 T3x2－2T5x＋T7＝0 を解け。
    ただし，a，b，cは実数で，Tn＝{(a－b)n＋(b－c)n＋(c－a)n}/n，
    (a－b)2＋(b－c)2＋(c－a)2≠0 とする。

  38. a+b+c=0のとき，次の等式を証明せよ。
    {(b-c)/a+(c-a)/b+(a-b)/c}{a/(b-c)+b/(c-a)+c/(a-b)}=9

  39. 3次方程式 x3+ax2+bx+c=0 の3つの解をα，β，γとするとき，
    α＋1/α，β＋1/β，γ＋1/γ を3つの解に持つ3次方程式を
    求めよ。ただし，x3の係数はcとする。


  40. 3次方程式 x3+px+q=0 の3つの解をα，β，γとするとき，次の比例式を証明せよ。
    (α2+β2+γ2)(α5+β5+γ5):(α3+β3+γ3)(α4+β4+γ4):(α7+β7+γ7)=10:6:7

  41. （中学生向け）
    正三角形ABCにおいて，BC，CA，AB上にそれぞれ点D，E，Fを
    BD＝CE＝AFとなるようにとり，BE，CFの交点をP，CF，ADの
    交点をQ，AD，BEの交点をRとする。
    △AFQ＝△PQR＝2√3のとき，次の問に答えよ。
    (1)　正三角形ABCの面積を求めよ。
    (2)　AFの長さを求めよ。ただし，AF＜FBとする。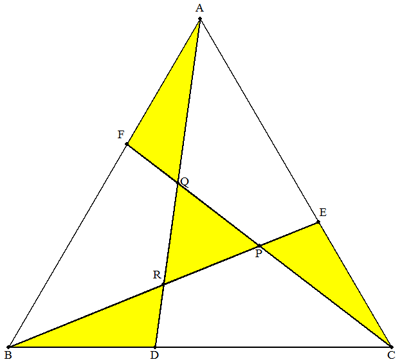

  42. 点P(a，b)と円x2+y2=r2について
    (1)　点Pから円に引いた接線の方程式を求めよ。ただし，a2+b2＞r2とする。
    (2)　(1)で，接点をそれぞれQ，Rとするとき，△PQRの面積を求めよ。
    (3)　直線QRの方程式を求めよ。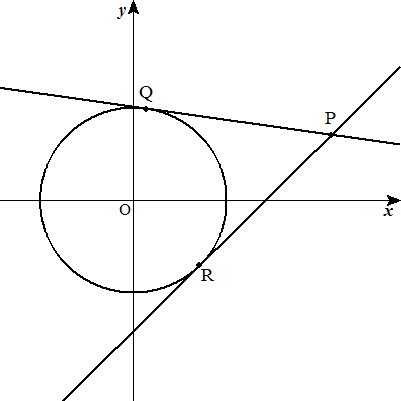
  43. （中学生向け）
    ひし形ABCDの辺BCの延長上に点Eをとり，AEとCD，BDとの交点を
    それぞれF，Gとするとき，∠BAG＝2∠BGA，EF=8，FG＝1であった。
    このとき，ひし形の面積を求めよ。
    また，EF=a，FG＝bのときの面積を求めよ。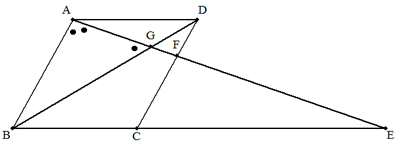
  44. （中学生向け）
    (1)　三角形ABCの辺BC，CA，AB上に点D，E，Fをとり，BEとCFの交点をP，
    CFとADの交点をQ，ADとBEの交点をFとする。三角形AFQ，BDR，CEPの面積が4，
    四角形AQPE，BRQF，CPRDの面積が11であるとき，三角形PQRの面積を求めよ。
    また，三角形AFQ，BDR，CEPの面積がa，四角形AQPE，BRQF，CPRDの面積がbで
    あるとき，三角形PQRの面積を求めよ。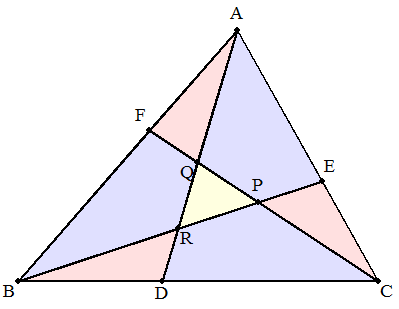
    (2)　三角形ABCの辺BC，CA，AB上に点D，E，Fをとり，BEとCFの交点をP，
    CFとADの交点をQ，ADとBEの交点をFとする。
    三角形AFQ，BDR，CEPの面積が1，四角形AQPEの面積が4，BRQFの
    面積が3，CPRDの面積が5であるとき，三角形PQRの面積を求めよ。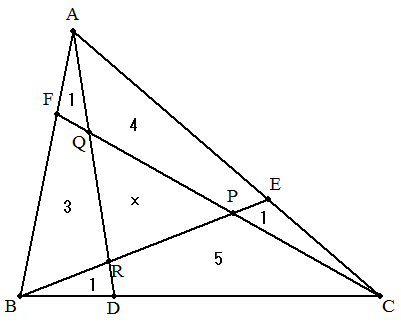
  45. （中学生向け）
    正方形ABCDの辺CD上に点Eを，BC＋CE＝AEとなるようにとり，
    CDの中点をFとすると，∠BAE＝2∠DAFであることを証明せよ。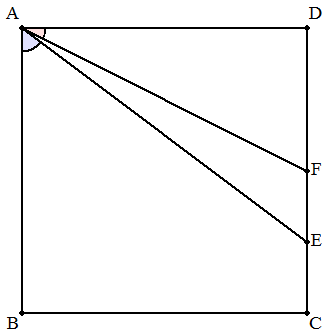
  46. （中学生向け）
    面積がsである平行四辺形ABCDの各辺に点E，F，G，Hを，BE:EC=1:1，
    CF:FD=2:1，DG:GA=1:3，AH:HB=4:1となるようにとる。
    また，AEとBFの交点をP，BFとCGの交点をQ，CGとDHの交点をR，DH
    とAEの交点をSとする。
    (1)　△BEPの面積を求めよ。
    (2)　四角形BPSHの面積を求めよ。
    (3)　四角形PQRSの面積を求めよ。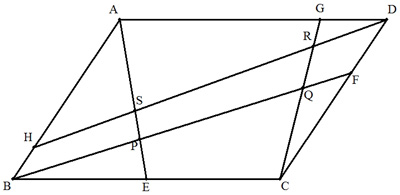

  47. 平行四辺形ABCDの各辺に点E，F，G，Hを，それぞれBE:EC=1:2，
    CF:FD=1:2，DG:GA=1:2，AH:HB=x:(1-x)（0<x<1）となるようにとる。
    また，AEとBFの交点をP，BFとCGの交点をQ，CGとDHの交点を
    R，DHとAEの交点をSとする。
    このとき，△AHS，△BEP，△CFQ，△DGR，四角形PQRSの面積
    和と四角形BPSH，四角形CQPE，四角形DRQF，四角形ASRGの
    面積和が等しいとき，xを求めよ。

  48. 平行四辺形ABCDの各辺に点E，F，G，Hを，それぞれBE:EC=
    a:(1-a)（0<a<1），CF:FD=b:(1-b)（0<b<1），DG:GA=c:(1-c)（0<c<1，
    1<a+b+c<2），AH:HB=x:(1-x)（0<x<1）となるようにとる。
    また，AEとBFの交点をP，BFとCGの交点をQ，CGとDHの交点
    をR，DHとAEの交点をSとする。
    このとき，△AHS，△BEP，△CFQ，△DGRの面積和が，四角形
    PQRSの面積と等しくなるとき，xをa，b，cを用いて表せ。
    また，a=b=c=2/5のとき，xを求めよ。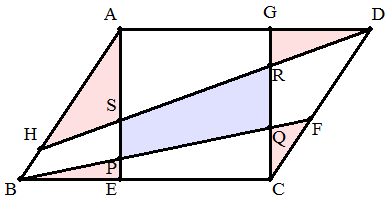
  49. （中学生向け）
    正方形ABCDの辺CDの中点をE，BEとACの交点をFとするとき，
    (1)　四角形AFED：正方形ABCDを求めよ。
    (2)　BF＝4のとき，四角形AFEDの面積を求めよ。
  50. （中学生向け）
    ∠A＝90°の直角二等辺三角形ABCの∠Bの二等分線に点Cから
    下ろした垂線の足をD，BDとACの交点をEとする。このとき，
    BE＝2ADを証明せよ。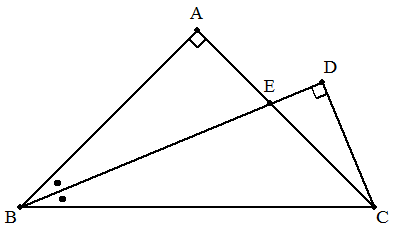