趣味の数学問題集・Ａ問題

■趣味の数学問題集・Ａ問題

（中学生向け）

三角形ABCの∠Aの二等分線とBCとの交点をD，
BCの延長上に点Eを，∠DAE＝90°となるよう
にとる。△ABD＝a，△ADC＝b（a>b）のとき，
△ACEの面積を求めよ。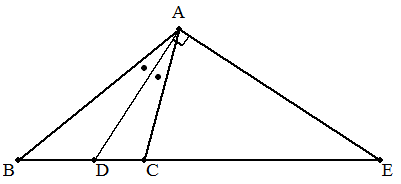

（中学生向け）

△ABCにおいて，AC，ABをa：bに内分する点をそれぞれD，Eとし，
BDとCEの交点をPとすると，AP＝CP＝a，BP＝√(a²+b²)であった。
△ABCの面積を求めよ。
例として，a＝3，b＝4のとき，△ABCの面積を求めよ。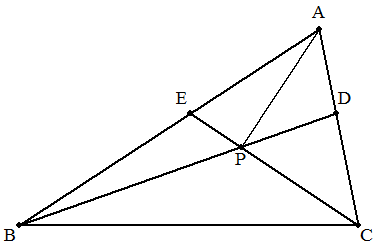

（中学生向け）

△ABCの重心をGとする。AB＝CG＝a，BG＝bのとき，
△ABCの面積を求めよ。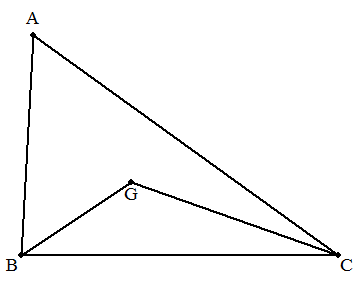
ひもを２つに切り，一方で円を，もう一方で正方形を作る。
このとき，円と正方形の面積和を最小にするには，ひもを
どの様に切ればよいか。
鋭角三角形ABCのBC，CA，ABの中点をそれぞれD，E，Fとする。
EF，FD，DEを内折りにし，頂点A，B，Cを重ねてできる四面体
A－DEFの体積を求めよ。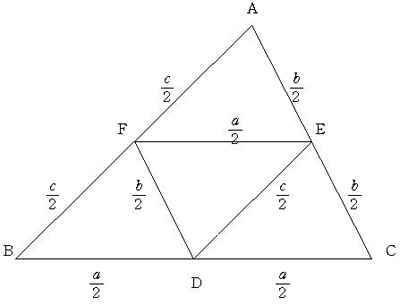
a>0のとき，x=(1+1/a)^a+1，y=(1+1/a)^aより，aを消去しx，yの関係式を求めよ。

三角形ABCについて，BCを3：4に内分する点をD，CAの中点をE，
ADとBEの交点をG，CGとABの交点をFとすると，GD＝9，GE＝14，
GF＝15であった。このとき，三角形ABCの面積を求めよ。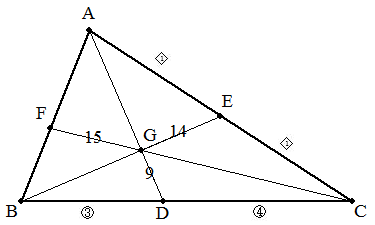

正方形ABCDにおいて，BCの中点をE，CDを2：1に内分する点をF，
点AからEFに引いた垂線とCD，EFとの交点をそれぞれG，Hとし，
△FHG，四角形CGHE，四角形AHFD，四角形ABEHに内接する
4つの円を順にP(r₁) ，Q(r₂) ，R(r₃) ，S(r₄) とするとき，r₁：r₂：r₃：r₄
を求めよ。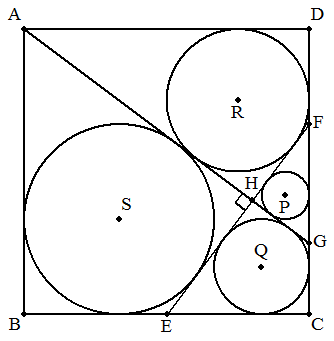

(1)	1辺aの正方形ABCDの頂点B，Cを中心とし，半径aの円を正方形内に描き，その各弧上に点P，Sをもち，かつ， BC上に2点Q，Rをもつ正方形PQRSを描く。このとき，PSに接し，かつ2つの弧に内接する円Tの半径をaを用いて表せ。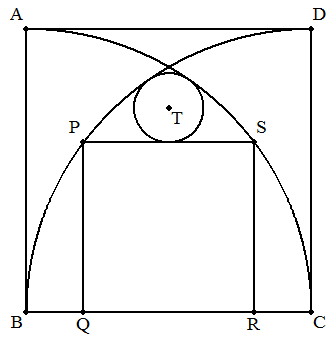
(2)	1辺aの正方形ABCDの頂点B，Cを中心とし，半径aの円を正方形内に描き，その各弧上に点Q，Rをもち，かつ， BCの中点Pをもつ正三角形PQRを描く。このとき，QRに接し，かつ2つの弧に内接する円Sの半径をaを用いて表せ。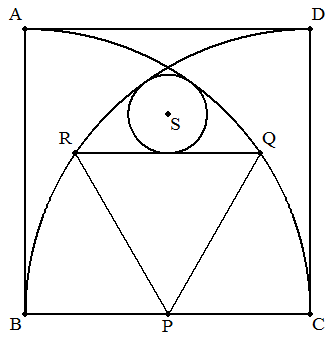

次を証明せよ。

(1)	点Oで交わる2つの線分AB，CDについて，OA＝OC，OB＝OD， ∠AOC＝60°である。3点P，Q，RをそれぞれOA，DO，BC上に OP/OA＝DQ/DO＝BR/BCとなるようにとると，三角形PQRは正三角形となる。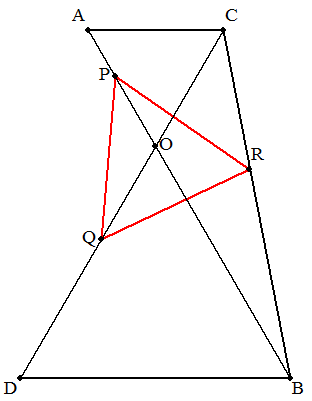
(2)	点Oで交わる2つの線分AB，CDについて，OA＝OC，OB＝OD， ∠AOC＝90°である。点D，Eを四角形AOCE，BODFが正方形になるようにとる。 4点P，Q，R，SをそれぞれOA，DO，FC，BE上に OP/OA＝DQ/DO＝FR/FC＝BS/BEとなるようにとると，四角形PQRSは正方形となる。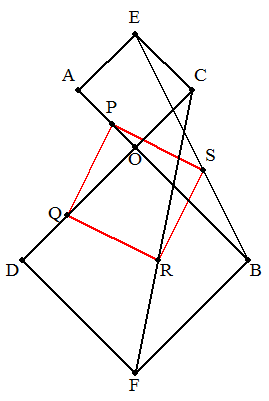
(3)	点Oで交わる2つの線分AB，CDについて，OA＝OC，OB＝OD， ∠AOC＝108°である。点E，F，G，Hを五角形AOCEF，BODGH が正五角形になるようにとる。 5点P，Q，R，S，TをそれぞれOA，DO，GC，HE，BF上に OP/OA＝DQ/DO＝GR/GC＝HS/HE＝BT/BFとなるようにとると，五角形PQRSTは正五角形となる。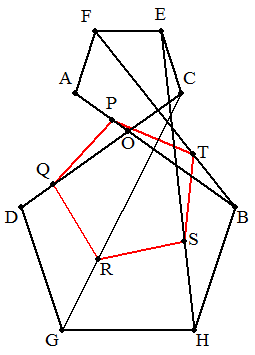

（中学生向け）

三角形OABのOA上に5個の点A₁，A₂，･･･，A₅をOに近い
ところから，OB上に5個の点B₁，B₂，･･･，B₅をOに近い
ところから，⊿OA₁B₁
＝⊿A₁B₁B₂＝⊿A₁A₂B₂
＝⊿A₂B₂B₃＝⊿A₂A₃B₃
＝⊿A₃B₃B₄＝⊿A₃A₄B₄
＝⊿A₄B₄B₅＝⊿A₄A₅B₅
＝⊿A₅B₅B＝⊿A₅AB
となるようにとる。
OA＝9，OB＝8のとき，OA₁，OB₁を求めよ。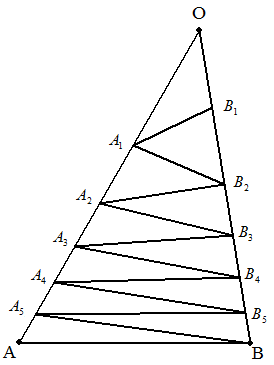

1辺aの正方形ABCDの頂点B，Cを中心とし，
半径aの円を正方形内に描き，さらに，
次のとおり8個の円を正方形内に描く。
弧BD，弧AC，BCに接する円をE(e)，
弧BD，弧AC，CDに接する円をF(f)，
弧BD，弧AC，DAに接する円をG(g)，
弧BD，弧AC，円Eに接する円をH(h)，
弧AC，円E，BCに接する円をI(i)，
弧BD，弧AC，円Fに接する円をJ(j)，
弧AC，円F，CDに接する円をK(k)，
弧AC，円E，円Iに接する円をL(l)とする。
このとき，円E，F，G，H，I，J，K，Lの半径を
それぞれaを用いて表せ。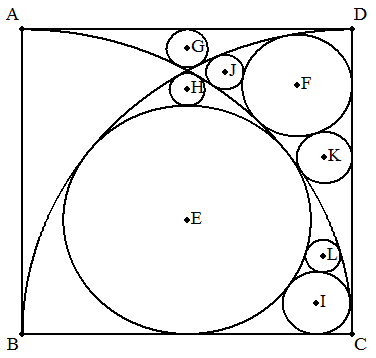

2014年から始まるn個の西暦の中から，1個を除き，平均を計算すると2046+1/13となった。
除いた西暦を求めよ。
（中学生向け）
1，2，3，･･･，n（nは奇数）の中から1個m（1≦m≦n）を除き，平均をとるとmになった。
mを求めよ。

(1)	1辺aの正方形ABCDの頂点B，Cを中心とし，半径aの円を正方形内に描き，その各弧上に点G，Jをもち，かつ， BC上に2点E，Fをもつ正六角形EFGHIJを描く。このとき，HIに接し，かつ2つの弧に内接する右図の円Kの半径をaを用いて表せ。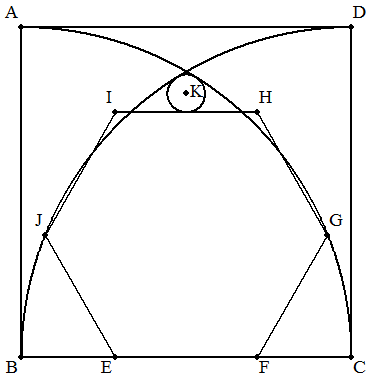
(2)	1辺aの正方形ABCDの頂点B，Cを中心とし，半径aの円を正方形内に描き，その各弧上に点S，Tをもち，かつ， BC上に2点P，Qをもつ正六角形PQRSTUを描く。このとき，STに接し，かつ2つの弧に内接する右図の円Vの半径をaを用いて表せ。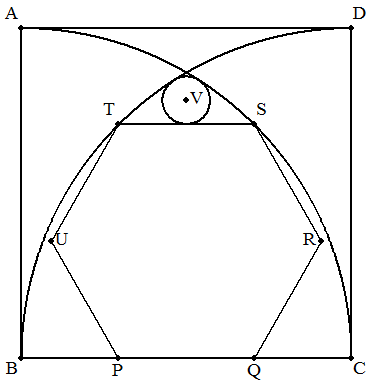

（中学生向け）

正方形ABCD内にCを中心とする扇形CBDと，BCを直径とする半円を描く。
半円上に点Eを取り，CEと扇形の交点をFとすると，∠ABF＝∠EBFである
ことを証明せよ。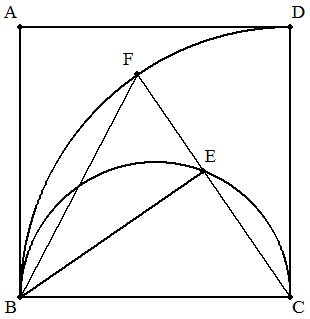

正三角形ABCとその頂点Aを通る円Tとの共有点が，図のようにP，Q，R，Sで，
AP=7，QR=2，AS＝5であるとき，正三角形の1辺と円の半径を求めよ。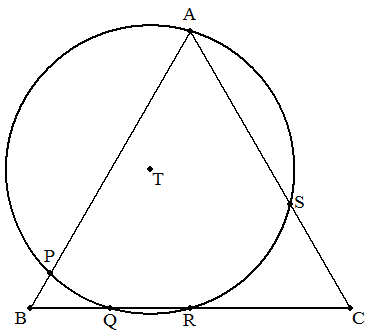

（中学生向け）

三角形ABCの外接円と三角形
ABCの3つの内角の二等分線の
交点をそれぞれD，E，Fとする。
点Dを通りEFに平行な直線をl₁，
点Eを通りFDに平行な直線をl₂，
点Fを通りDEに平行な直線をl₃
とする。
l₂，l₃の交点をL，
l₃，l₁の交点をM，
l₁，l₂の交点をNとする。
このとき，三角形ABCの内心I
と三角形LMNの外心は一致
することを証明せよ。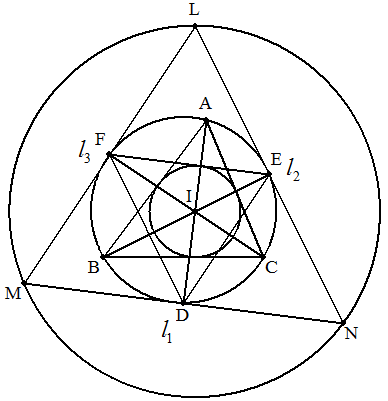

BC＝27，AC＝8，∠BCA＝90°である△ABCについて，
ABの中点をDとする。BCの延長上に点Eをとり，EAの
延長上に点Fを，FB⊥BEとなるようにとる。DE＝DFの
とき，EFの長さを求めよ。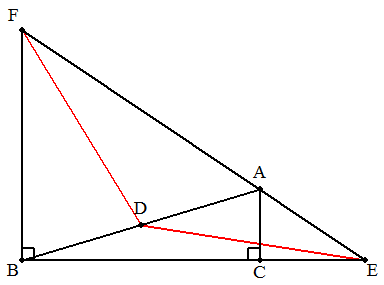

3つの平行線l₁，l₂，l₃が図のように与えられている。
l₁，l₂，l₃上に順に1点ずつA，B，Cをとり，
正三角形ABCを作図せよ。

1辺の長さがaの正方形ABCDの中心をOとする。
各頂点を中心としてOを通る4つの円を正方形内
に描くときにできる4つの花弁の面積（斜線部分）
を求めよ。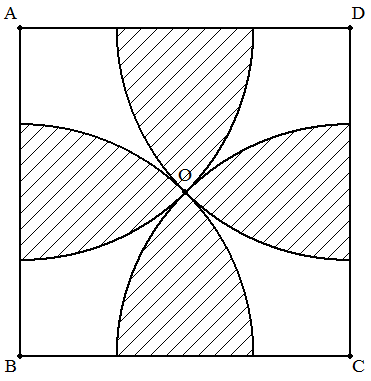

1辺の長さがaの正方形ABCDとこれをその中心の周りにαだけ
回転させた正方形EFGHとの共通部分の面積をSとする。
(1)　Sを求めよ。
(2)　Sが正方形の5/6になるとき，sinαの値を求めよ。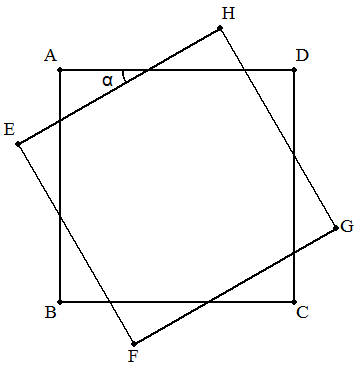

半径1の円に正三角形ABCと正方形DEFGが内接している。次の場合について，正三角形と正方形の重なった部分の面積を求めよ。 (1)　BC∥EF
(2)　点A，Gが一致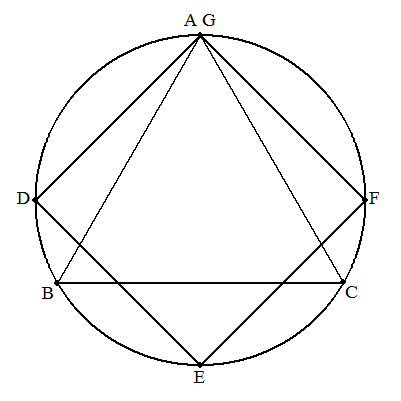

1辺の長さがaである正六角形ABCDEFの4辺AB，
CD，DE，FAの中点をそれぞれG，H，I，Jとし，GE
とCJの交点をK，BIとCJの交点をL，BIとHFの
交点をM，GEとHFの交点をNとする。
次の面積を求めよ。
(1)　四角形AGKJ
(2)　四角形GBLK
(3)　三角形BCL
(4)　四角形KLMN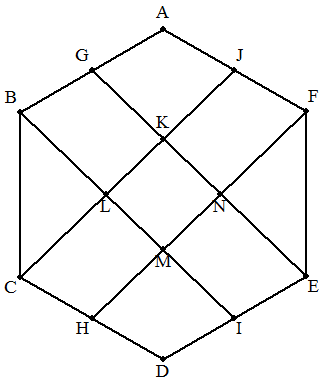

1辺の長さがaである正方形ABCDの辺AB，BC，
CD，DAの中点をそれぞれE，F，G，Hとし，EDと
AFの交点をI，AFとBGの交点をJ，BGとCHの
交点をK，CHとEDの交点をLとする。
次の面積を求めよ。
(1)　三角形AEI
(2)　四角形AILH
(3)　四角形IJKL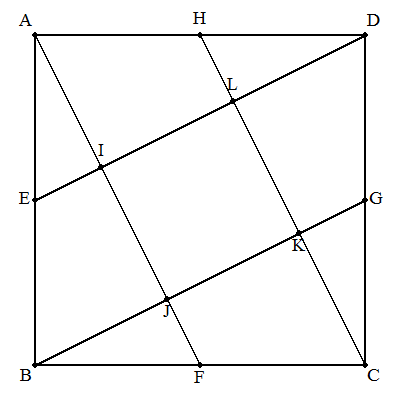

nは5以上の奇数とする。円周上にn個の点をとり，1つおきに繋いでできる星形多角形の内角の和（赤い角の総和）を求めよ。

n=5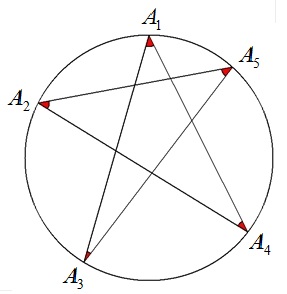
n=7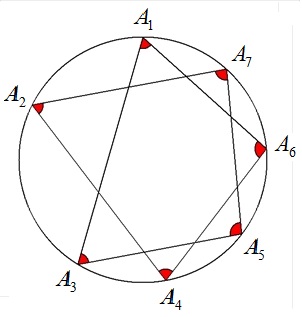
n=9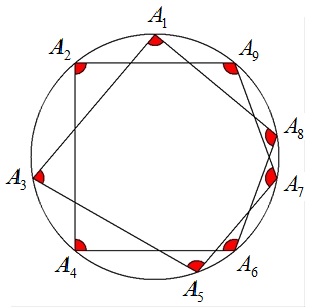
nは5以上の奇数とする。円周上にn個の点をとり，(n-1)/2個おきに繋いでできる星形多角形の内角の和（赤い角の総和）を求めよ。

n=5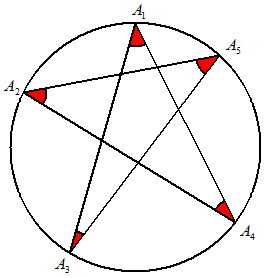
n=7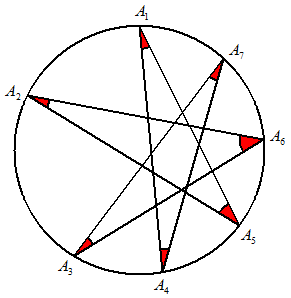
n=9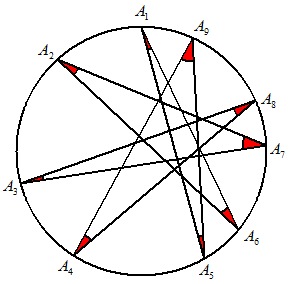
正方形ABCDを右の図のように5つの長方形で分割する。
周りの4つの長方形の面積が等しいとき，中央の長方形
は正方形になることを証明せよ。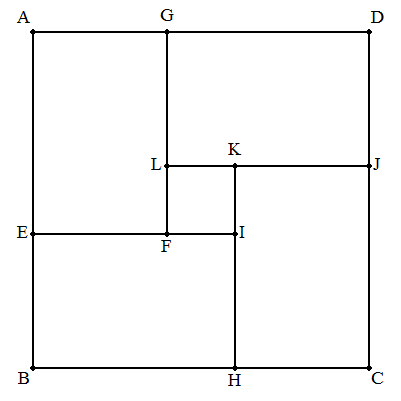
(1-i)²⁰¹⁴を計算せよ。ただし，iは虚数単位で，2の累乗は計算しないでそのままの形でよい。
2定点A，Bからの距離の比がm:n（m≠n）である点Pの軌跡は，円になることが知られている（アポロニウスの円）。
その円の中心は，線分ABをm²:n²に外分する点であることを証明せよ。
与えられた三角形ABCの外部に，∠APB＝45°，∠APC＝30°となる点Pを作図せよ。
（右図の通り，2通りある。）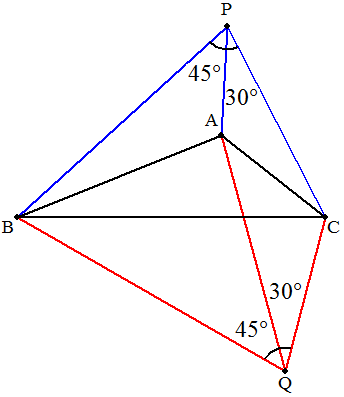

1辺の長さがaである正八角形ABCDEFGHの4辺
AB，DE，EF，HAの中点をそれぞれI，J，K，Lとし，
DLとFIの交点をP，DLとBKの交点をQ，HJとBK
の交点をR，HJとFIの交点をSとする。
四角形PQRSの面積を求めよ。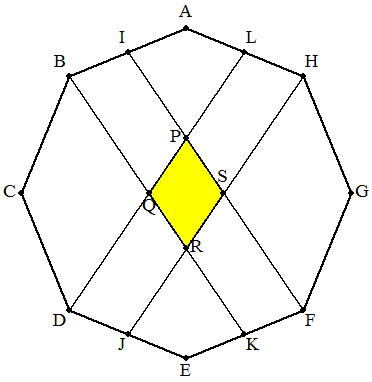

3つの同心円が図のように与えられている。
同心円の外側から周上に順に1点ずつA，B，Cをとり，
正三角形ABCを作図せよ。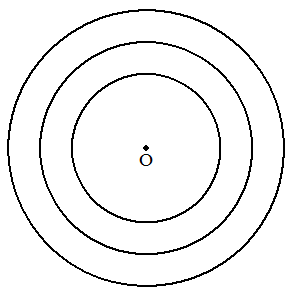
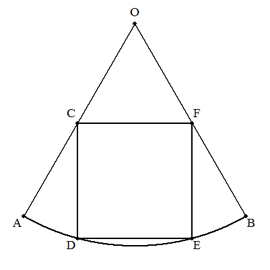
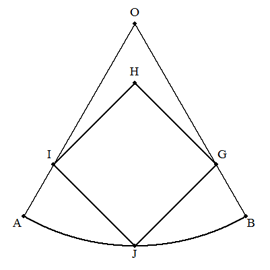
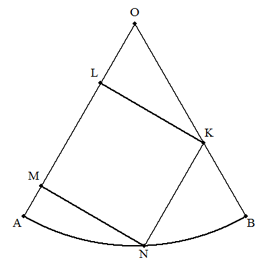
半径r，中心角60°の扇形OABに，（ア），（イ），（ウ）のように正方形を内接させる。
（ア）の正方形CDEFは，DE∥ABである。
（イ）の正方形GHIJは，Jが弧ABの中点である。
（ウ）の正方形KLMNは，辺LMがOA上にある。
このとき，それぞれの正方形の1辺を求めよ。

（ア）（イ）（ウ）
（中学生向け）

三角形ABCの外心をO，垂心をHとする。
OからBCに下ろした垂線の足をMとする
とき、AH＝2OMを証明せよ。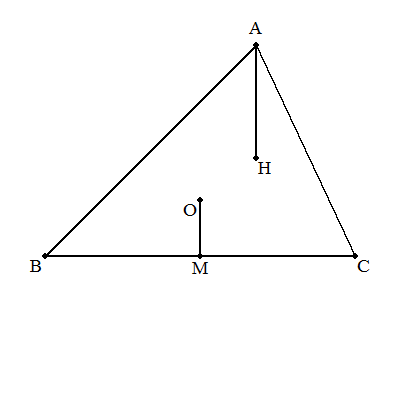

図のように，4直線k，l，m，nは平行で，
点Aは直線kの上側に，点Bは直線nの
下側にある。点Cを直線k上にとり，
Cから直線lに下ろした垂線の足をDと
する。また，点Eを直線m上にとり，
Eから直線nに下ろした垂線の足をFと
する。このとき，AC＋CD＋DE＋EF＋FB
が最小になるようなAC，CD，DE，EF，FB
を作図せよ。

水平な地にある3つの観測点A，B，Cはこの順に
一直線上にあり，AB＝BC＝a（km）である。
ある時刻にこの3地点から飛行機（P）を見ると，
仰角がそれぞれα，β，γであった。
飛行機の高度（PQ）（km）を求めよ。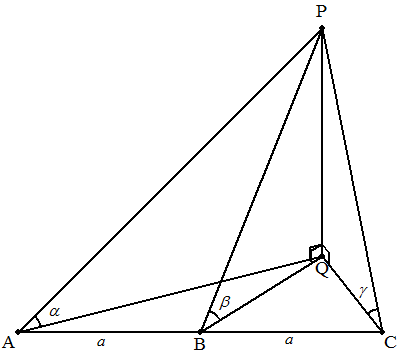

△ABCについて，BCの中点をD，BC＝a，CA＋AB＝eとする。
ADが最小になるとき，△ABCの面積を求めよ。

4直線k，l，m，nは，図のようにk∥l，
m∥nである。点Aは直線kの上側に，
点Bは直線nの下側にある。点Cを直線
k上にとり，Cから直線lに下ろした垂線
の足をDとする。また，点Eを直線m上に
とり，Eから直線nに下ろした垂線の足を
Fとする。このとき，AC＋CD＋DE＋EF＋FB
が最小になるようなAC，CD，DE，EF，FB
を作図せよ。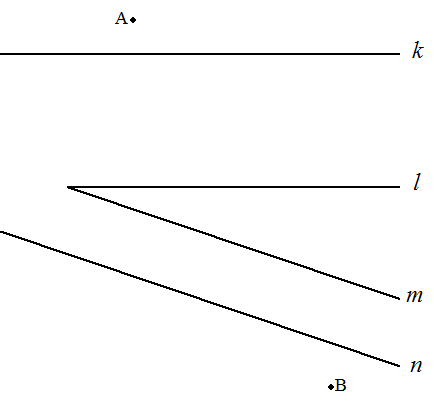

川岸k，lが平行である川と，
川岸m，nが平行である川が，
図のように合流している。
川岸kの上方にA地点，川岸lとm
の間にB地点，川岸nの下方にC
地点がある。AからB，BからC，
CからAに最短で行けるように
川に橋を架けたい。ただし，
橋は川に対して垂直に架けられ
るものとし，人一人が通れる幅
とする。図に，AからB，BからC，
CからAに最短で行ける経路を
図示せよ。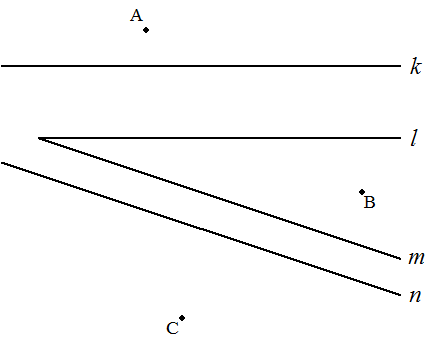

半径1，中心角120°の扇形OAB
内に図のように等円P，Qを内接
させ，さらに円Rを円P，Qに
外接させOA，OBに内接させる。
このとき，
(1)　円Pの半径を求めよ。
(2)　円Rの半径を求めよ。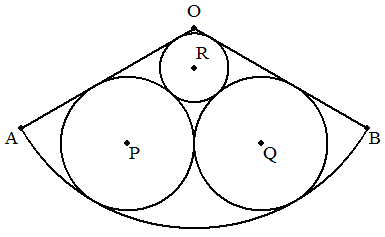

正三角形ABC内に図のように
4つの円が含まれている。
円Pは，AB，BCに接し，半径3
円Qは，BC，CAに接し，半径3
円Rは，CA，ABに接し，半径1
円Sは，円P，Q，Rに外接し，
半径2である。
正三角形の1辺を求めよ。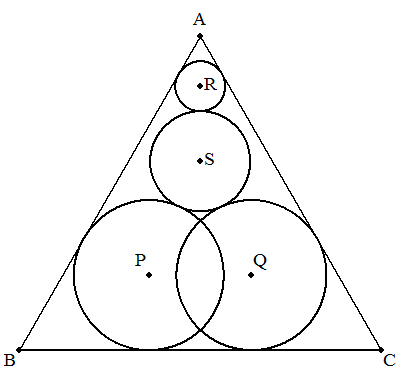

正三角形ABC内に図のように
4つの円が含まれている。
円Pは，AB，BCに接し，半径a
円Qは，BC，CAに接し，半径a
円Rは，CA，ABに接し，半径b
円Sは，円P，Q，Rに外接し，
半径cである。
正三角形の1辺を求めよ。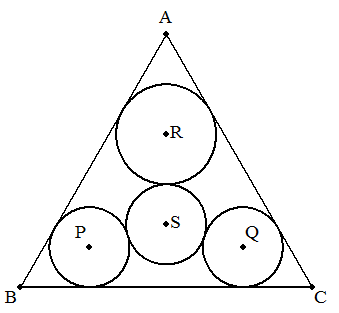

A=90°の△ABCについて，ABの中点Dから
BCに下ろした垂線の足をEとする。
BE＝1，EC＝5のとき，AEを求めよ。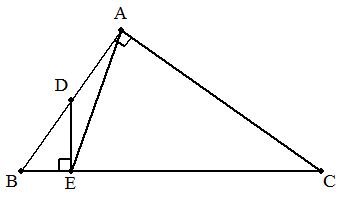

△ABCの頂点B，Cを通る円と，AB，ACとの交点をD，Eとする。
BC上に点F，Gを，DF∥AC，EG∥ABとなるようにとる。このとき，次を証明せよ。
(1)　4点D，E，F，Gは同一円周上にある。
(2)　四角形DBGE：四角形DFCE＝AB²：AC²

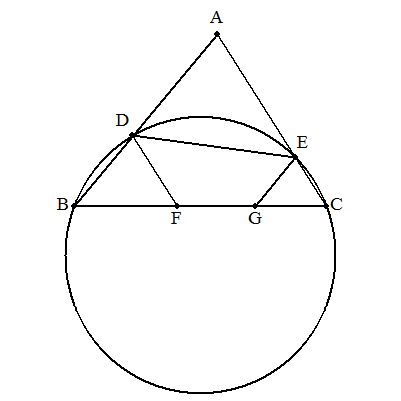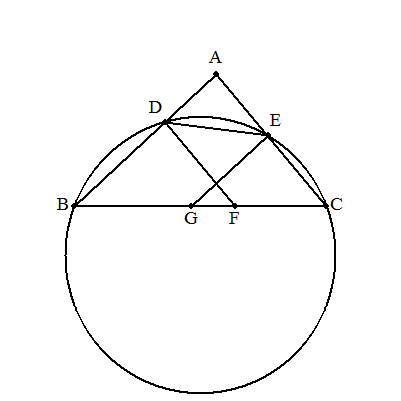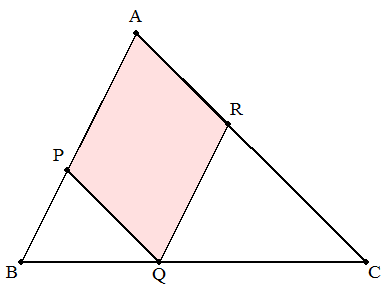
△ABCのBC上に点Qをとり，点PをAB上にPQ∥ACとなるように，
点RをAC上にRQ∥ABとなるようにとる。平行四辺形APQRの面積が
最大になるとき，点QはBCの中点であることを証明せよ。

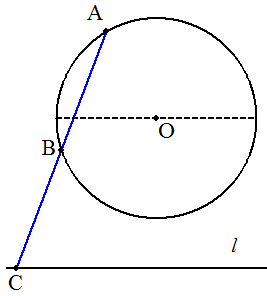
右の図のように定円Oと定直線lがある。
点Aは直線lに平行な直径より上の方の
円周上にとる。
点Aから直線lに交わる直線を引き，円O
と直線lとの交点をそれぞれB，Cとする。
このとき，AB＝BCとなる点Bを円周上に
求めよ。（作図せよ。）

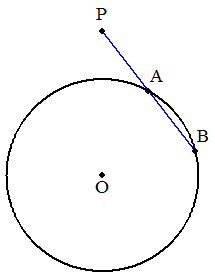
円O外の1定点Pより割線PABを引き，
PA＝ABとなる点Aを求めよ。
（図示せよ。）
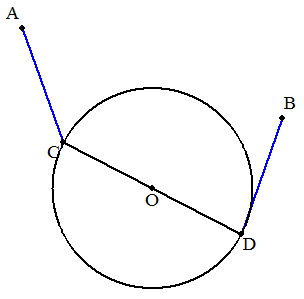
円O外に2定点A，Bがあり，直径CDを
引いてAC＝BDとなる点Cを求めよ。
（図示せよ。）

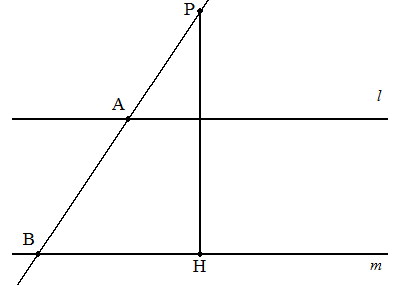
図のように2直線l，mは平行で，直線lの上方に点Pがある。
点Pからmに下ろした垂線の足をHとする。
点Pを通る直線と，l，mとの交点をそれぞれA，Bとする。
AB＝BHとなる直線PBを引け。（作図せよ。）

（ア）	（イ）	（ウ）