■趣味の数学問題集・Ａ問題

  1. 大小2つの同心円の大円に，
    図のようにAB＝BC＝CDと
    なる弦ADを作図せよ。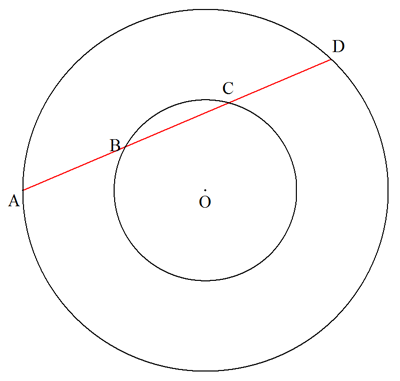

  2. 正方形ABCD内にAP:CP=1:2，BP:DP=3:4となる点Pを
    図示せよ。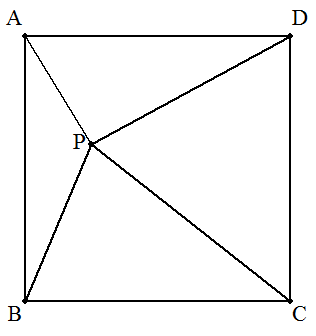

  3. 1直線lの同じ側に2円A，Bがある。l上に1点Pを求めて，
    Pからこの2円に接線PD，PEを引き，これとlとのなす角
    が等しくなるようにせよ。
    また，このような点Pはいくつあるか。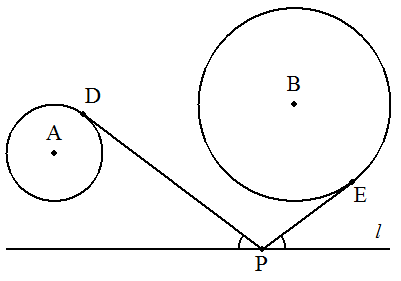

  4. 直線lの同じ側に2円Q，Rがあり，半径はそれぞれ3，2，
    中心距離QR=7，円の中心Q，Rから直線lに下ろした垂線の
    足をそれぞれH，Iとすると，QH＝6，RI＝4であった。
    l上の点Pから2円に引いた接線の長さが等しくなるとき，
    (1)　接線の長さAPを求めよ。
    (2)　HP：PIの比を求めよ。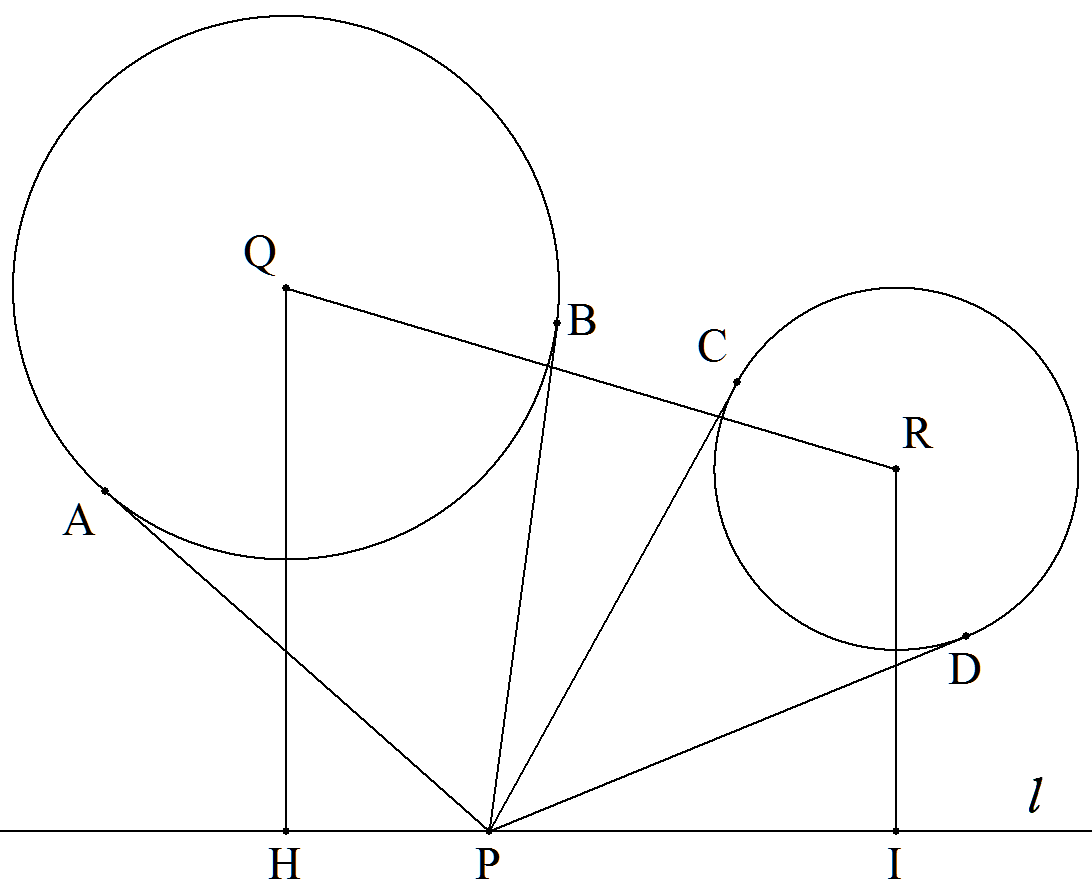
  5. （中学生向け）
    2円O，Pの一方の円の中心からもう一方の円への
    接線を互いに引く。
    このとき，図の弦ABと弦CDの長さは等しい。
    （眼球の定理）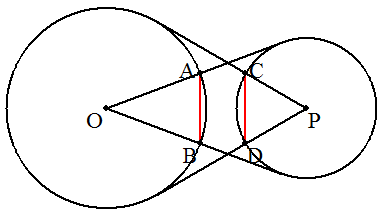

  6. 2点A，Bの中点Mを，コンパスのみで作図せよ。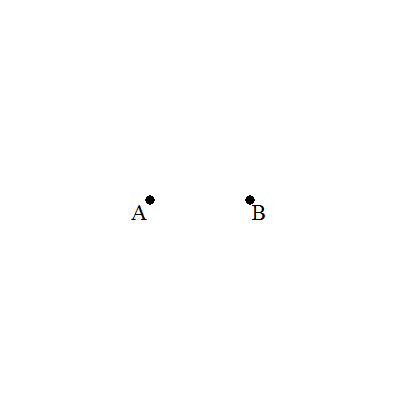

  7. 六角形ABCDEFの面積を点Aを通る線分APで
    二等分したい。点Pを辺上に求めよ。

  8. 三角形ABC内に点Sを，∠SAB＝∠SBC＝∠SCAとなるようにとる。
    (1)　点Sを作図で求めよ。
    (2)　∠SAB＝ωとおくとき，1/tanω＝1/tanA+1/tanB+1/tanC
    　を証明せよ。
    (3)　ω≦30°を証明せよ。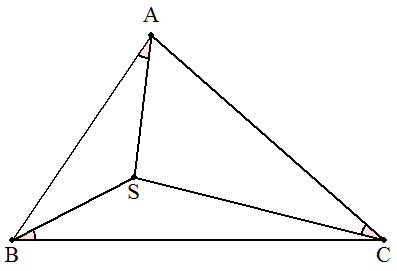

  9. 半径5の円O内に点Pを，OP＝4となるようにとる。
    点Pを通り，長さ8の弦ABを作図せよ。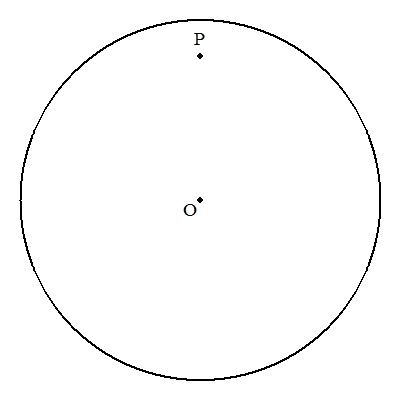

  10. 図のように2円O，Pがあり，円Oの周上の点Aを通る
    直線を引いて，2円との交点を図のように，B，C，D
    とする。AB＝CDとなる線分ADを作図せよ。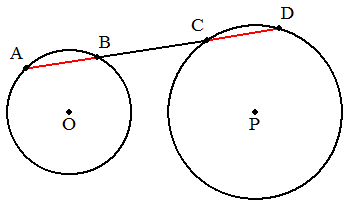

  11. 3つの箱の中に合計n個のボールが入っている。
    どの箱にも同じ個数のボールが入っている確率を求めよ。


  12. (1) 半径rの円Oの外周に図のように12個の等円A，B，･･･，Lを
    互いに外接するように配置する。
    円Aの半径を求めよ。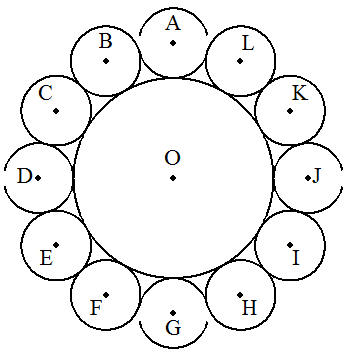
    (2)半径rの円Oの内周に図のように12個の等円A，B，･･･，Lを
    互いに外接するように配置する。
    円Aの半径を求めよ。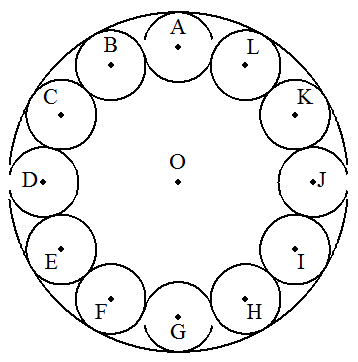

  13. 与えられた4点A，B，C，Dを4つの辺上に持つ正方形PQRSを作図せよ。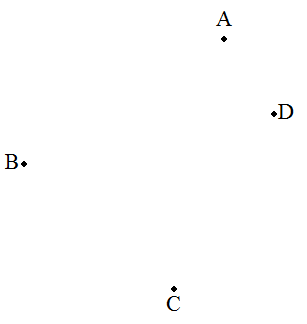

  14. 円内に2点P，Qが図のように与えられている。
    直角三角形の直角をはさむ辺の一方がPを含
    み，他方の辺がQを含むように，その円内に
    内接する直角三角形を作図せよ。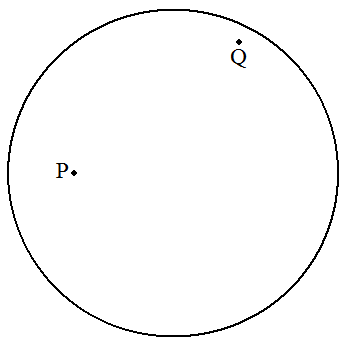

  15. 2点A，Bで交わる2円について，Aを
    通る直線と2円との交点を図のよう
    にC，Dとする。
    AC＝ADとなる線分CDを作図せよ。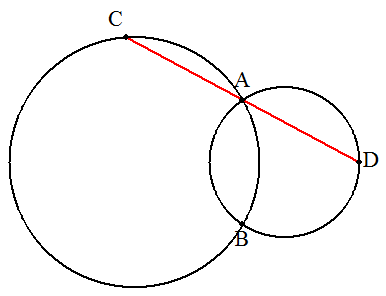

  16. 与えられた三角形ABCと等積な正方形CDEFを作図せよ。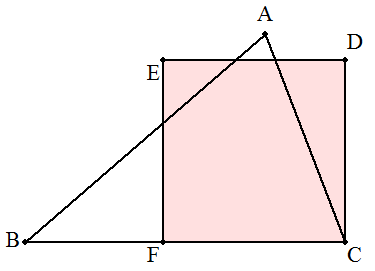

  17. 与えられた三角形ABCと等積な正三角形CDEを作図せよ。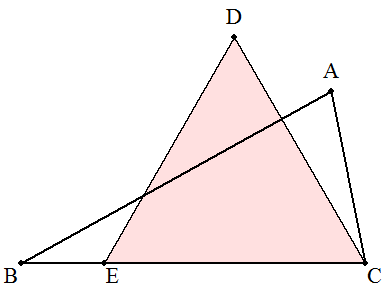

  18. C=90°である△ABCの各辺を1辺にもつ正方形
    ABDE，BCFG，CAHIを△ABCの外側に作る。
    このとき，DG2＋EH2＝5AB2を証明せよ。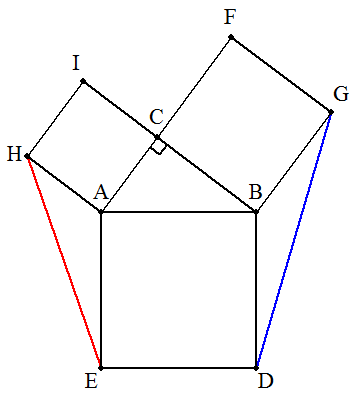

  19. 文字a，b，cがそれぞれn個ずつ合計3n個ある。
    次の場合に，同じ文字が隣り合わないように1列に並べる順列の総数を求めよ。
    (1)　n＝2のとき
    (2)　n＝3のとき
    (3)　n＝4のとき


  20. △ABCと等積な∠Aを共有する
    直角三角形ADEを作図せよ。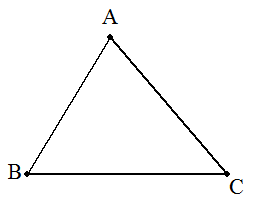

  21. 3辺の比BC：CA：AB＝2：1：√3である三角形ABCについて，
    BCを1辺とする正方形BDECを△ABCの外側につくる。
    DE上に点Pを，APが五角形ABDECの面積を二等分するように
    とる。
    (1) 点Pの位置を作図によって求めよ。
    (2) DP：PE＝1：kとおくとき，kの値を求めよ。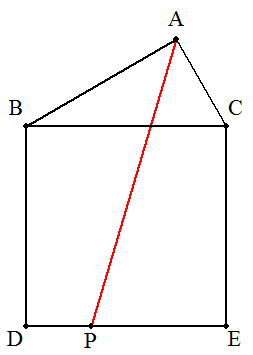
  22. （中学生向け）
    △ABCのBCを1辺とする正方形BDECを△ABCの外側につくり，
    BCからDEに下ろした垂線の足をH，AHとBCの交点をIとする。
    DE上に点Pを，APが五角形ABDECの面積を二等分するように
    とる。
    (1) 点Pの位置を作図によって求めよ。
    (2) △ABC，長方形BDHI，長方形IHECの面積をそれぞれS1，
    S2，S3とおくとき，DP：PE＝(S1＋S3)：(S1＋S2)となることを証明
    せよ。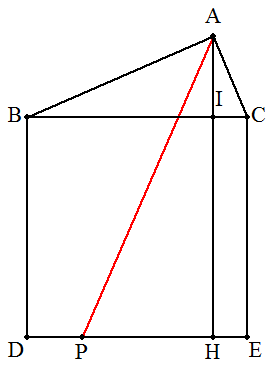

  23. （中学生向け）
    正方形ABCDの辺BC，DAの中点をそれぞれM，Nとする。
    ACとBNの交点をP，AMとBDの交点をQ，
    ACとDMの交点をR，BDとCNの交点をPとする。
    このとき，正方形ABCDは4つの直線PS，QR，PQ，SR
    によって9個の合同な正方形に分割されることを証明
    せよ。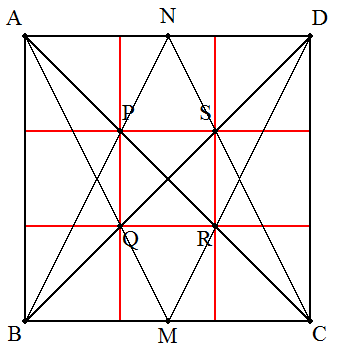
  24. （中学生向け）
    ∠A＝90°である直角二等辺三角形ABCの3辺BC，CA，
    ABをm：nに内分する点をそれぞれL，M，Nとする。
    このとき，LM，LN，AM，ANを直径とする4円は，1点Pで
    交わることを証明せよ。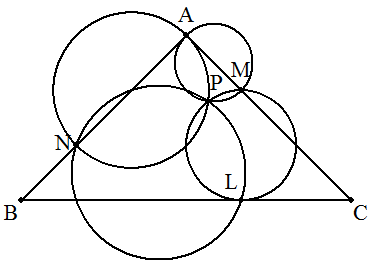

  25. 交わる2直線a1x+b1y+c1=0…①，a2x+b2y+c2=0…②について，
    ①から距離h1，②から距離h2である点は4個考えられる。
    それらの4点を頂点とする四角形の面積を求めよ。

  26. （中学生向け）
    ∠A＝90°の直角二等辺三角形ABCのBCの中点をDとし，右の図
    のように直角二等辺三角形DEFを，EF上に点Aがあるようにつくる。
    ABとDFの交点をG，ACとDEとの交点をHとする。BG＝a，CH＝bと
    おくとき，EFを求めよ。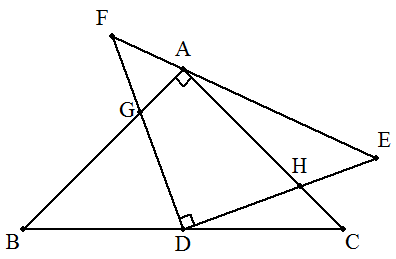
  27. （中学生向け）
    ∠A＝90°の△ABCについて，BCの中点をD，CA，AB上に
    それぞれ点E，Fを，∠FDE＝90°となるようにとる。
    (1)　BC＝10，DE＝3，DF＝4のとき，△ABCを作図せよ。
    (2)　△ABCの面積を求めよ。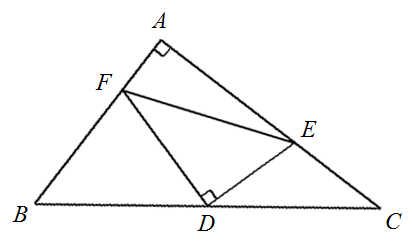

  28. ∠A＝90°，BC＝aである△ABCについて，BCの中点Dを
    頂点に持つ1辺tの正三角形DEFが△ABCに内接している。
    △ABCの面積を，a，tを用いて表せ。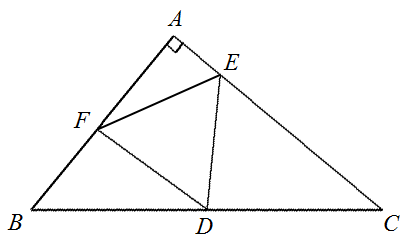

  29. x2=x1-2a(ax1+by1+c)/(a2+b2)， y2=y1-2b(ax1+by1+c)/(a2+b2)
    のとき，
    x1=x2-2a(ax2+by2+c)/(a2+b2)， y1=y2-2b(ax2+by2+c)/(a2+b2)
    となることを証明せよ。

  30. 直交座標に2つの動点P，Qがある。P，Qの速さの比はp：qで，
    一定の速さで点Pはx軸上を，点Qはy軸上をそれぞれ正の向き
    に進む。点P，Qの初めの位置をそれぞれA0，B0，1秒後の位置
    をそれぞれA1，B1，2秒後の位置をそれぞれA2，B2，…，n秒後
    の位置をそれぞれAn，Bnとする。
    A0B0＝d0，A1B1＝d1，A2B2＝d2のとき，次の問いに答えよ。
    (1)　P，Qの秒速をそれぞれ求めよ。
    (2)　AnBnを求めよ。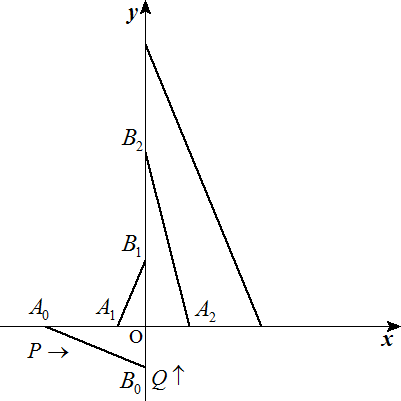

  31. 四角形ABCDの各頂点より対角線に下ろした垂線の足を
    E，F，G，Hとすると，四角形EFGHは四角形ABCDと相似
    であることを証明せよ。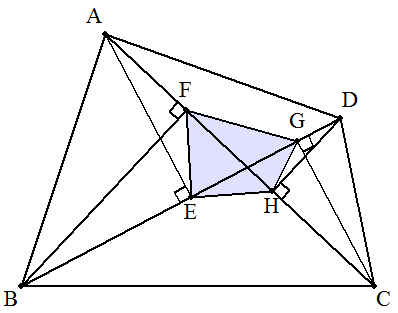

  32. 3式
    2c{(a/2)2+y2-x2}=(c2+a2-b2)y…①
    2b{(a/2)2+z2-x2}=(a2+b2-c2)z…②
    bc{(c-y)2+(b-z)2-2x2}=(b2+c2-a2)(c-y)(b-z)…③
    より，y2+(c-y)2=z2+(b-z)2 を導け。
    ただし，文字はすべて正の数とする。

  33. Zを整数の集合とする。
    (1)　集合A＝{n|n＝a2＋b2，a∈Z，b∈Z}は，積の演算について閉じていることを証明せよ。
    (2)　集合B＝{n|n＝a3＋b3＋c3－3abc，a∈Z，b∈Z，c∈Z}は，積の演算について閉じていることを証明せよ。

  34. △ABCの頂点AからBCに下ろした垂線の足を
    D，頂点B，Cから∠Aの二等分線に下ろした
    垂線の足をそれぞれE，Fとし，3点D，E，Fを
    通る円とBCとの交点のうち，Dでない方を，G
    とする。GはBCの中点であることを証明せよ。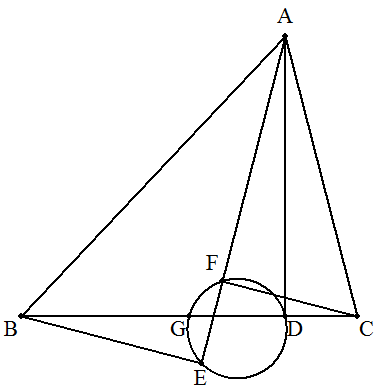

  35. (1) （小学生向け）
    円に外接する正三角形ABCと内接する正三角形
    DEFがある。2つの正三角形の面積比を求めよ。
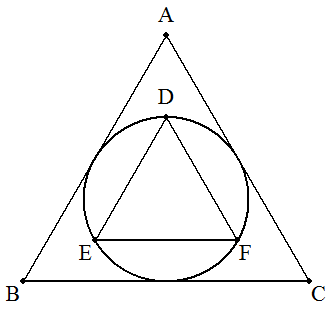    (2) （小学生向け）
    円に外接する正方形ABCDと内接する正方形
    EFGHがある。2つの正方形の面積比を求めよ。
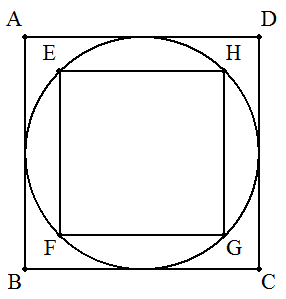    (3) 円に外接する正五角形ABCDEと内接する正五角形
    FGHIJがある。2つの正五角形の面積比を求めよ。

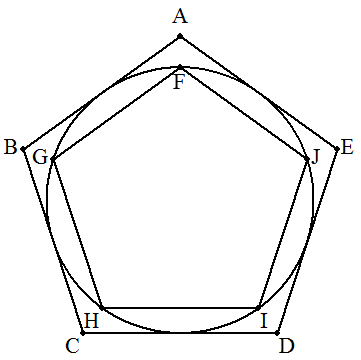  36. △ABCにおいて，頂点AからBCに下ろした
    垂線の足をD，DからCA，ABに下ろした
    垂線の足を，それぞれE，Fとする。
    同様に，頂点BからCAに下ろした垂線の足
    をG，GからAB，BCに下ろした垂線の足を，
    それぞれH，Iとし，頂点CからABに下ろした
    垂線の足をJ，JからBC，CAに下ろした垂線
    の足を，それぞれK，Lとする。
    このとき，EF＝HI＝KLとなることを証明せよ。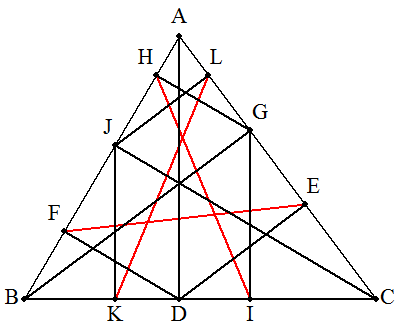

  37. △ABCについて，BCの中点をD，CA，AB上に
    それぞれ，点E，Fを，図のように，△DEFが
    直角二等辺三角形になるようにとる。
    このとき，AE2+EC2＝AF2+FB2
    となることを証明せよ。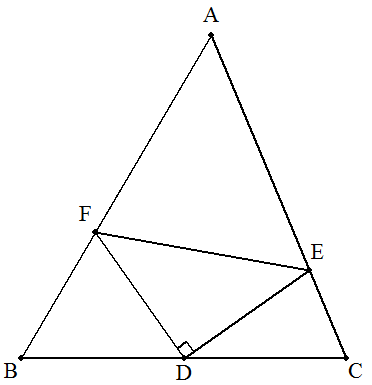

  38. △ABCについて，BCの中点をD，CA，AB上に
    それぞれ，点E，Fを，図のように，△DEFが
    直角二等辺三角形になるようにとる。
    AE＝11，EC＝2，AF＝10のとき，
    (1)　DEを求めよ。
    (2)　△ABCの面積を求めよ。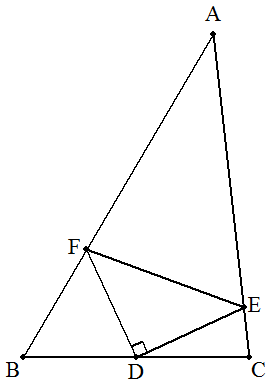

  39. 原点中心，半径1の円Oと3点A(1,0)，
    B(0,1)，C(-1,0)がある。弧AB上に点Dを
    とり，弧BC上に点Eを，∠DOE＝90°と
    なるようにとる。
    点DがAからBまで動くとき，ADとCEの
    交点Pの軌跡の方程式を求めよ。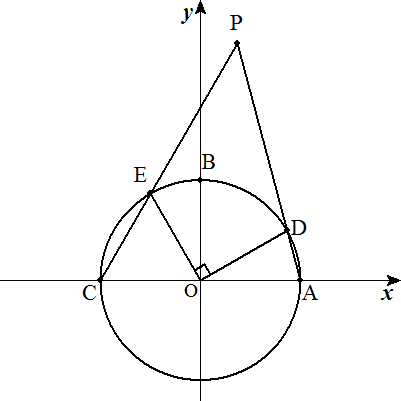

  40. △ABCのBCの中点をDとし，CA上に点E
    を，DC＝DEとなるように，AB上に点Fを，
    DB＝DFとなるようにとる。DE＝DFとなる
    とき，DE，DFは△AEFの外接円の接線
    になることを証明せよ。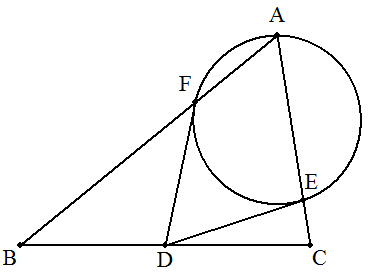

  41. △ABCのBからCAに下ろした垂線の足をD，
    DからABに下ろした垂線の足をE，
    CからABに下ろした垂線の足をF，
    FからCAに下ろした垂線の足をG，
    DEとFGの交点をHとする。
    次の4つの直角三角形の面積比を求めよ。
    △AFG：△ADE：△HDG：△HFE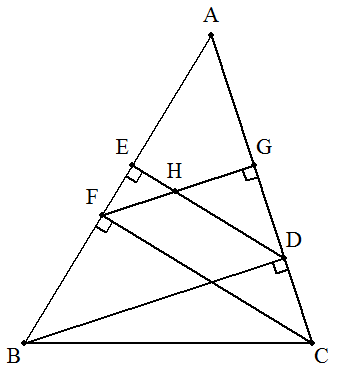

  42. △ABCの頂点B，Cから対辺に下ろした垂線の足を
    それぞれD，Eとし，BDとCEの交点をFとする。
    AB＝11，AC＝10，FC＝2のとき，次の長さを求めよ。
    (1)　BF
    (2)　BC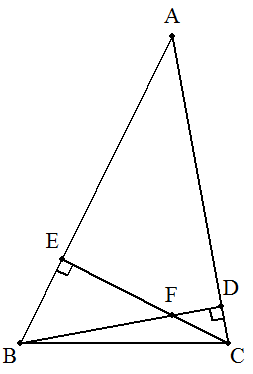

  43. (1)　(12＋22)(32＋42)＝22＋112＝52＋102のように，2つの自然数の平方和の積は，
    2通りの2つの自然数の平方和の形に表すことができることを証明せよ。
    (2)　(12＋22)(32＋42)(52＋62)(72＋82)を2つの自然数の平方和として表せ。

  44. 線分ABは2円の共通弦である。AB上の点Cを
    通る直線が2円と交わる点を，図のように
    P，Q，R，Sとする。
    PQ=8，QC=4，CR=3のとき，RSを求めよ。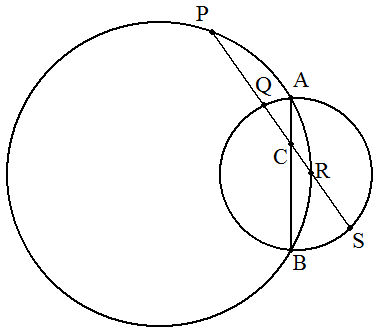

  45. AB＝ACである三角形ABCのBC上に点Dをとる。
    AD=5，BD=9，CD=16のとき，ABを求めよ。

  46. 外接する2円O，Pの共通接線ABを作図せよ。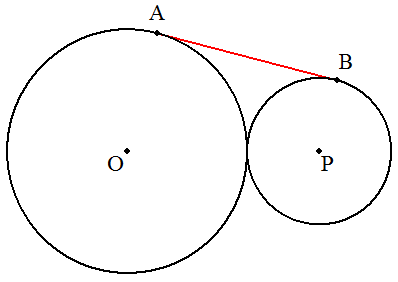

  47. (1)　図のように2円O，Pがあり，共通外接線ABを作図せよ。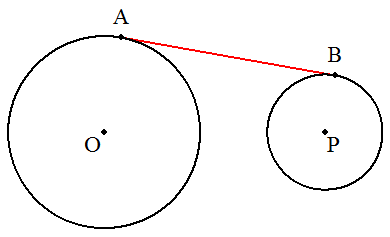
    (2)　図のように2円O，Pがあり，共通内接線ABを作図せよ。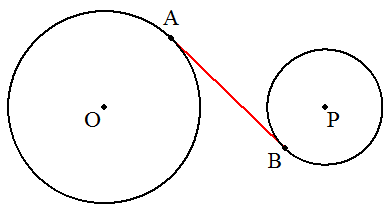

  48. 4個の合同な正三角形ABC，DEF，GHI，JKL
    が図のように重ねられている。MはKLの中点
    で，5点A，D，G，J，Mは一直線上にあり，
    AM⊥KLで，BC∥EF∥HI∥KLである。
    この図形のまわりの長さが6のとき，AMの長さ
    を求めよ。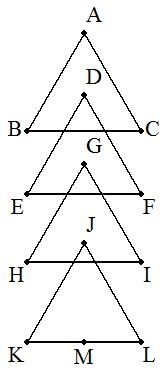

  49. △ABCの垂心S，重心J，外心Gは1直線上にあり，
    SJ＝2JGであることを証明せよ。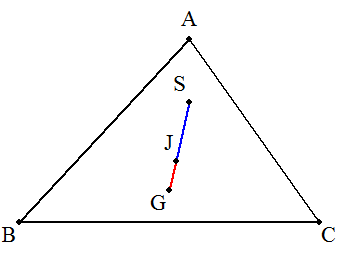

  50. 円に内接する四角形ABCDの各辺に頂点をもつ
    ひし形を作図せよ。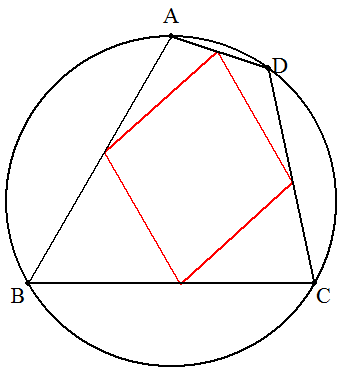