■趣味の数学問題集・Ａ問題

  1. AB＝ACの△ABCのBCとDE＝DFの△DEFのEFが
    互いに垂直二等分線となり，点Mで交わっている。
    ABとDE，DFの交点をそれぞれG，H，
    ACとDF，DEの交点をそれぞれI，Jとすると，
    4点G，H，I，Jは，同一円周上にあることを証明せよ。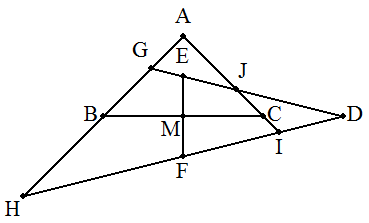

  2. AB＝6，BC＝8，CD＝3，DA＝4である円に内接する
    四角形ABCDの各辺に頂点をもつひし形について，
    (1)　一辺の長さを求めよ。
    (2)　面積を求めよ。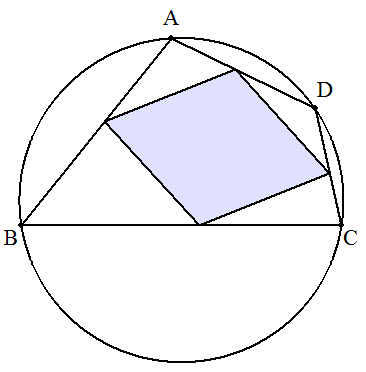

  3. 円に内接する六角形ABCDEFの対角線AD，BE，CF
    が1点Pで交わっている。AB＝14，BC＝16，CD＝20，
    DE＝21，EF＝12のとき，FAの長さを求めよ。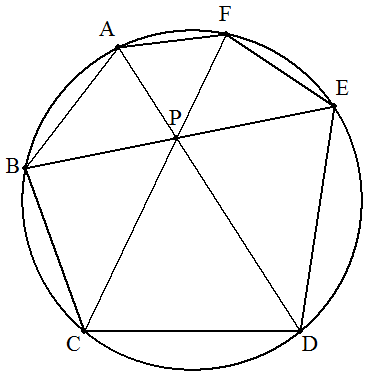

  4. 1から9までの数字を順に使い，例にならって2015を作れ。
    （169番の類題）
    （例）
    2014＝1234－5＋6！－7＋8×9
    2014＝123＋45－6！－7－8－√9
    2014＝(－1＋2＋3＋4＋5×6)×(7×8－√9）
    2014＝1×2×(3＋√4×5＋6)×(7×8－√9)


  5. 正四面体O-ABCの辺OA，OB，OC上にそれぞれ点D，E，Fを，
    OD＝a，OE＝b，OF＝cとなるようにとる。このとき，
    (1)　△DEFの面積Sを求めよ。
    (2) 三角錐O－DEFの体積Vを求めよ。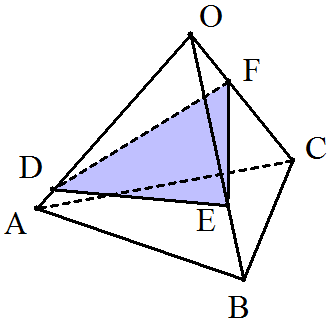

  6. f(x，y，z)＝x－x2(y＋z)/(x2＋y2＋z2)とおく。
    f(x，y，z)＝f(y，x，z)，x≠yのとき，次の式の値を求めよ。
    (1)　f(x，y，z)－f(z，y，x)
    (2)　(1/x+1/y+1/z)f(x，y，z)

  7. a，bは整数で，0＜a/71＜1，0＜b/100＜1を満たしている。
    このとき，｜a/71－b/100｜の最小値と，そのときのa，bの値を求めよ。

  8. a，bを2桁の正の整数とする。
    a÷bの計算を電卓で行ったら，1.2131147と表示された。
    a，bの値を求めよ。

  9. 52円切手x枚と82円切手y枚を買うと，その代金は2,300円になった。
    x，yの値を求めよ。

  10. 袋の中に赤玉1個，青玉2個，白玉3個が入っている。
    この袋の中から玉を1個取り出し，色を確かめてから玉を元に戻す。
    この試行を繰り返すとき，次の問に答えよ。
    (1) 赤玉を1回取り出すか，青玉を2回取り出すか，白玉を3回取り出したとき，
    この試行は終了する。試行が終了する回数の期待値を求めよ。
    (2) 青玉を2回取り出すか，白玉を2回取り出したとき，試行は終了する。
    ちょうどn回で試行が終了する確率を求めよ。

  11. 自然数1，2，3，･･･，nの中から1個mを取り除く。このとき，残った自然数のうち，
    1からm－1までの和とm＋1からnまでの和が等しくなった。
    m，nの値の組を3通り求めよ。ただし，1<m<nとする。

  12. 4つの整数1234，2340，3446，5500をある正の整数で割るとどれも割り切れないで，
    余りは等しくなった。ある正の整数と余りを求めよ。

  13. △ABCにおいて，頂点AからBCに下ろした垂線の足をD，
    DからCA，ABに下ろした垂線の足を，それぞれE，Fとする。
    同様に，頂点BからCAに下ろした垂線の足をG，
    GからAB，BCに下ろした垂線の足を，それぞれH，Iとし，
    頂点CからABに下ろした垂線の足をJ，
    JからBC，CAに下ろした垂線の足を，それぞれK，Lとする。
    また，JLとGH，DFとJK，GIとDEの交点を，それぞれP，Q，Rとする。
    このとき，六角形DRGPJQの面積を三角形の3辺a，b，cを用いて表せ。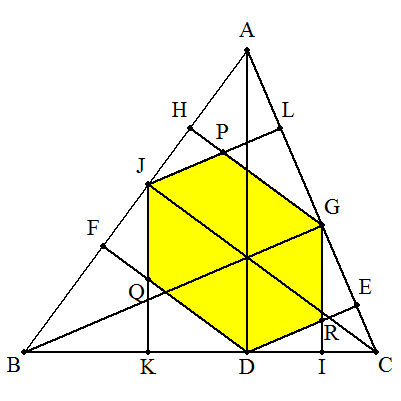

  14. 互いに平行でない3直線 a1x+b1y+c1=0，a2x+b2y+c2=0，a3x+b3y+c3=0 によって
    作られる三角形の面積を求めよ。

  15. 次の10進法の小数を，3進法の小数で表せ。
    (例)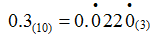　
    (1)　0.13(10)
    (2)　0.123(10)

  16. 六角形ABCDEFは円に内接しており，
    AB=BC=CD=11，DE=EF=FA=2のとき，
    円の半径を求めよ。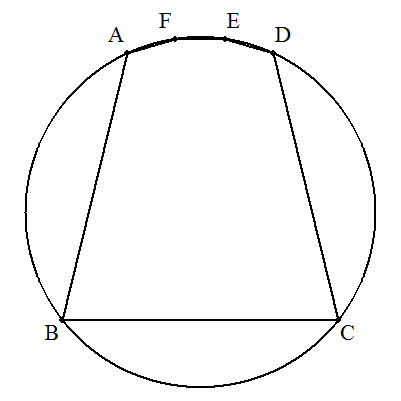

  17. 六角形ABCDEFは円に内接しており，
    AB=BC=8，CD=DE=17，EF=FA=22のとき，
    円の半径を求めよ。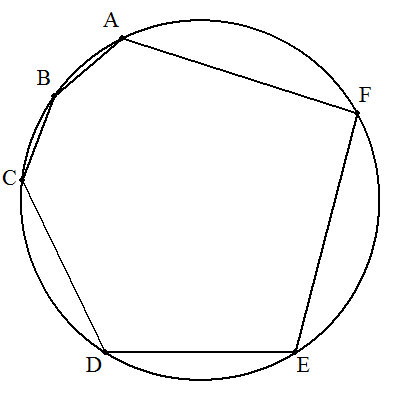

  18. 容器Aにはp（%）の食塩水a（g），容器Bにはq（%）の食塩水b（g）が入っている。
    それぞれの容器から同じ量の食塩水を取り出し，それぞれをもう一方の容器に入れる。
    このとき，
    (1)　容器Aの濃度がr（%）のとき，容器Bの濃度を求めよ。ただし，p>r>qとする。
    (2)　容器A，Bの濃度が同じになるとき，それぞれ取り出した食塩水の量を求めよ。

  19. 容器A，B，Cに，それぞれ18％，12％，9％の食塩水が入っている。
    容器Aに入っている食塩水525gからx（g）を容器A1に，y（g）を容器A2に入れる。
    同様に，容器Bに入っている食塩水420gからx（g）を容器B1に，y（g）を容器B2に入れ，
    容器Cに入っている食塩水630gからx（g）を容器C1に，y（g）を容器C2に入れる。
    次に，B2とC1に入れた食塩水を容器Aに，C2とA1に入れた食塩水を容器Bに，
    A2とB1に入れた食塩水を容器Cに入れると，容器A，B，Cの濃度がすべて同じになった。
    このとき，x，yの量をそれぞれ求めよ。

  20. 方眼用紙に図のように，ABを対角線に持つ長方形と
    その中心に半径5の円が描かれている。円の内部を
    通らずにAからBまで行く最短経路は何通りあるか。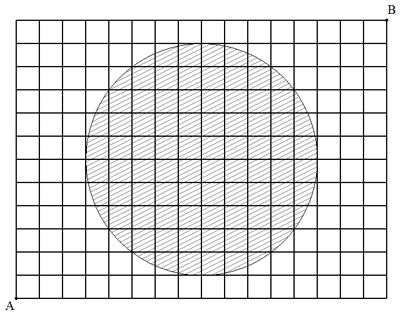

  21. 長方形ABCDの対角線dの半分の長さを直径とする円が，
    長方形の中心にある。その円の内部を通らないで点Aから
    Cまで最短経路で進むとき，その距離をdを用いて表せ。

  22. 川沿いにA町があり，そこから下流にa（km）離れたところにB町がある。
    この2つの町をつなぐ船は，下りにt時間かかる。
    ある日，B町からA町に船が上っていった。
    しかし，途中で船が故障したため、船は数分間流されてしまった。
    その後故障が直り，再び川を上り始めた。
    その結果，下りの2倍の時間を要してA町に着いた。
    上りの速さは，下りの速さのk倍（1/2<k<1）であるとき，
    船が故障で流された時間は何分か求めよ。

  23. 2018をいくつかの自然数に分け，それらの積をつくる。
    このとき，その積の最大値を素因数分解した形で求めよ。


  24. 4人の子をもつ母親が言いました。
    4人の子の年齢の積は144だけど，年齢の和を知っても，4人の子の年齢は特定できないわ。
    また，双子はいないし，上の子から下の子まで順に並べたとき，隣り合う子の年齢差は3歳以下です。
    4人の子の年齢を小さい方から順に答えてごらん。

  25. △ABCの辺BCの中点をDとし，辺CA，AB上にそれぞれ
    点E，Fを，△DEFが正三角形になるようにとる。このとき，
    (1) 3AE2＋EC2＝3AF2＋FB2を証明せよ。
    (2) AE＝7，EC＝5，AF＝6のとき，
    　正三角形の1辺およびBCを求めよ。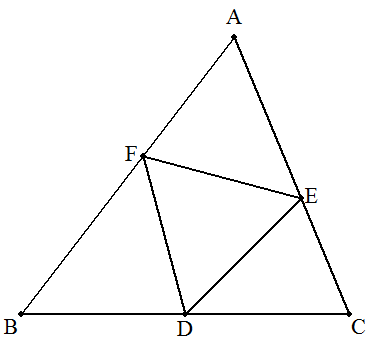

  26. BC=5，CA=7，AB=8である△ABCの辺BCの中点をDとし，
    辺CA，AB上にそれぞれ点E，Fを，△DEFが正三角形に
    なるようにとる。このとき，正三角形の1辺を求めよ。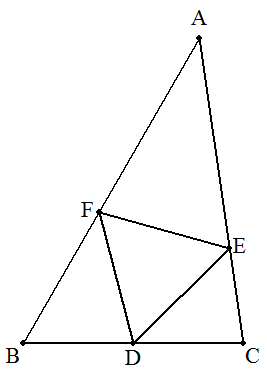

  27. △ABCの辺BCの中点をDとし，三角形内に正六角形DEFGHIを
    図のように頂点G，Hが三角形の辺上にあるようにつくる。
    AG＝2，GC＝13，AH＝4のとき，正六角形の1辺を求めよ。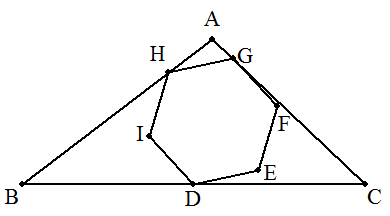

  28. (1)　A＝120°である二等辺三角ABCと点Pがある。
    　AP＝√3，BP＝5，CP＝4のとき，△ABCの面積を求めよ。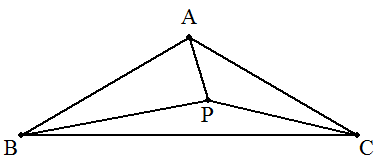
    (2)　A＝120°である二等辺三角ABCと点Pがある。
    　AP＝5，BP＝√19，CP＝8のとき，△ABCの面積を求めよ。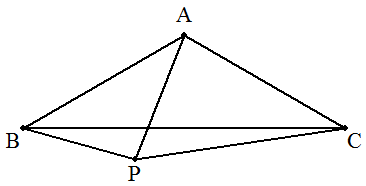

  29. 四角形ABCDの対角線の交点をEとし，
    DAを1：2に内分する点をPとする。
    △ABE＝1，△CDE＝5のとき，
    凹形四角形PBECの面積を求めよ。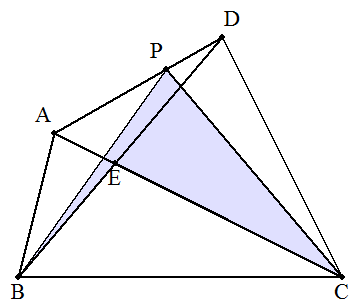

  30. 逆ピラミッド型の足し算パズル
    (1)　隣同士の数字の和を下に記入し，これを続けていく。
    　　最後の答を求めよ。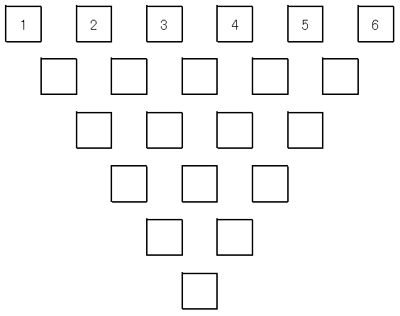
    (2)　最後の答が123となるように，初めの1行目の6箇所の
    　　枠に，1～6までの数字を入れよ。
    　　ただし，1通りの答でよい。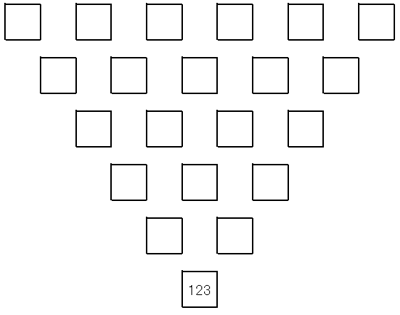
    (3)　最後の答が345となるように，初めの1行目の6箇所の
    　　枠に，1，2，4，8，16，32の6個の数字を入れよ。
    　　ただし，1通りの答でよい。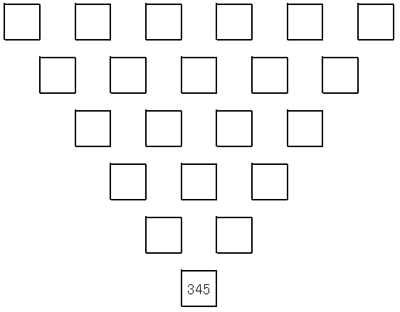

  31. 正三角形ABC内に点Dを次のようにとるとき，正三角形の1辺を求めよ。
    (1)　AD＝2，BD＝1，∠BDC＝150°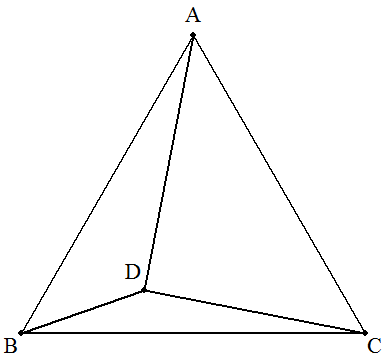
    (2)　AD＝3，BD＝4，CD＝5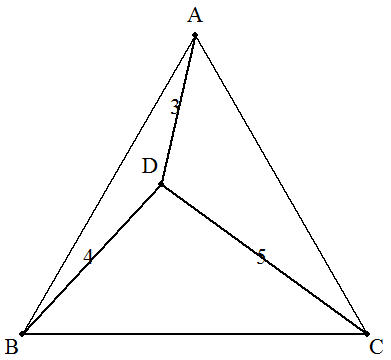

  32. 正三角形ABCと点Dについて，AD＝1，BD＝2，CD＝3のとき，
    正三角形の1辺を求めよ。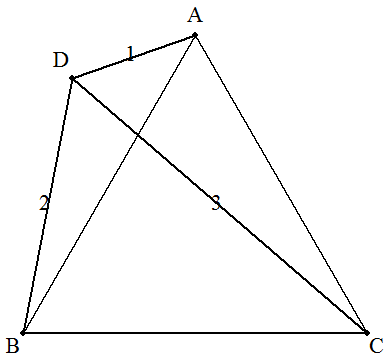

  33. 正五角形の作図法を一つ述べよ。

  34. 四角形ABCDは半径rの円に内接し，
    DA＋AB＝a，BC＝CD＝bのとき，
    DA，ABの長さをそれぞれ求めよ。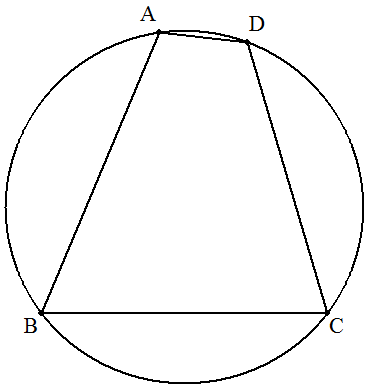

  35. 1辺aの正五角形ABCDEのBC上に点Fを，
    DE上に点Gを，FG∥CDで，FGは正五角形
    の面積を二等分するようにとる。
    このとき，FGの長さを求めよ。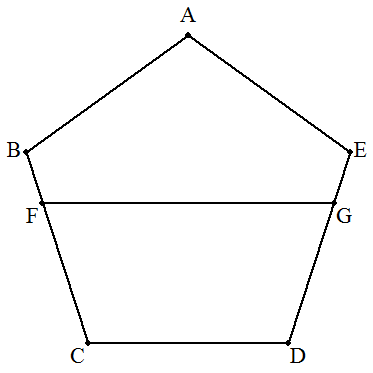

  36. 正三角形の土地を，塀を建てて仕切り，2等分する。その際，
    塀の長さを最小にするには，どのように立てたらよいか。


  37. 3辺の長さがa，3，4である△ABCの内接円，外接円の半径をそれぞれr，Rとする。
    (1)　rRの値の範囲を求めよ。
    (2)　rR＝2のとき，rを求めよ。

  38. AB=4,BC=6,CD=5,DA=3である四角形
    ABCDとその内接円との接点を，図の
    ようにE，F，G，Hとする。EG⊥FHの
    とき，四角形ABCDの面積を求めよ。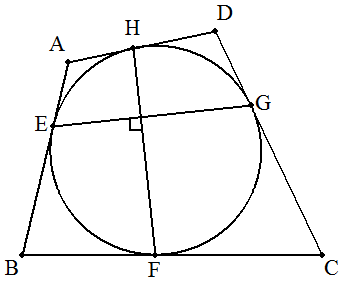

  39. コインの直径を1として，次のサイズの箱の中に重ならないように並べる。最大何個並べられるか。
    (1)　10×10
    (2)　16×16

  40. a+b+c=p，1/(a+b)+1/(b+c)+1/(c+a)=qのとき，
    a/(b+c)+b/(c+a)+c/(a+b)の値をp，qを用いて表せ。

  41. a+b+c=0のとき，次の等式を証明せよ。
    {(b-c)/a+(c-a)/b+(a-b)/c}{a/(b-c)+b/(c-a)+c/(a-b)}=9

  42. 正三角形ABCの辺BC上に点Dをとり，辺CAを2：1
    に内分する点をEとする。点FをABに関して点Cと
    反対側に△ECD≡△EFDとなるようにとる。
    ABとDF，EFとの交点をそれぞれG，Hとする。
    △DCG∽△HAFとなるとき，BD：DCを求めよ。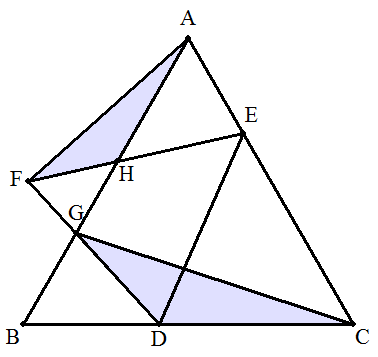

  43. (1)　正三角形ABC内の1点Pから，BC，CA，ABに
    　　下ろした垂線の足をそれぞれD，E，Fとすると，
    　　PD＋PE＋PFは一定であることを証明せよ。
    (2)　△ABC内に点Pをとる。AP＋BP＋CPが最小
    　　になる点Pを求めよ。ただし，三角形の内角は
    　　どれも120°より小さいものとする。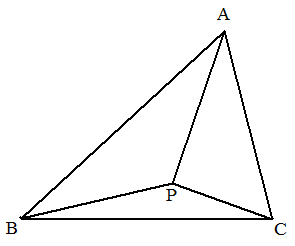

  44. 平行四辺形ABCDについて，
    ABをk：(1-k)に内分する点をE，
    BCをl：(1-l)に内分する点をF，
    CDをm：(1-m)に内分する点をGと
    する。
    ただし，0＜k，l，m＜1とする。
    また、CEとFGの交点をP，
    APの延長とBCとの交点をQとするとき，
    AP：PQを求めよ。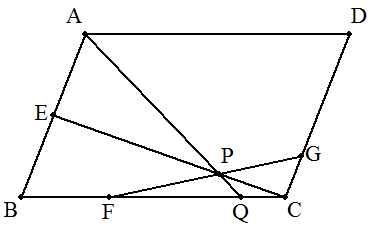

  45. 平行四辺形ABCDについて，
    ABをk：(1-k)に内分する点をE，
    BCをl：(1-l)に内分する点をF，
    CDをm：(1-m)に内分する点をG，
    DAをn：(1-n)に内分する点をHと
    する。
    ただし，0＜k，l，m，n＜1とする。
    また，EGとFHの交点をP，
    APの延長とBCとの交点をQとするとき，
    AP：PQを求めよ。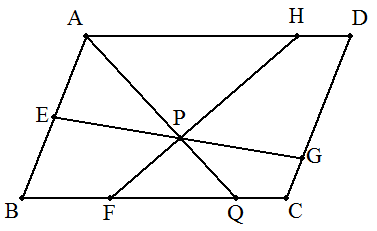

  46. 平行四辺形ABCDについて，
    ABを1：1に内分する点をE，
    BCを1：3に内分する点をF，
    CDを1：2に内分する点をG，
    DAを1：4に内分する点をHと
    する。
    また，ACとEH，FGとの交点
    をそれぞれP，Qとするとき，
    AP：PQ：QCを求めよ。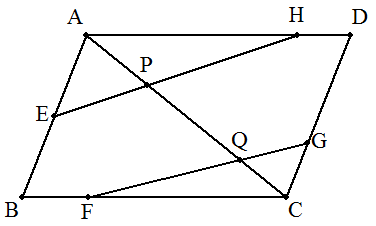

  47. 平行四辺形ABCDについて，
    AB，BC，CD，DA上にそれぞれ
    点E，F，G，Hをとり，ACとEH，
    FGとの交点をそれぞれP，Qとする。
    いま，
    AE：EB＝k：(1-k)，AH：HD=l：(1-l)，
    CF：FB＝m：(1-m)，CG:GD＝n：(1-n)，
    1/k+1/l=1/a，1/m+1/n=1/bとおくとき，
    AP：PQ：QCをa，bを用いて表せ。
    ただし，0<k，l，m，n<1 とする。

  48. （中学生向け）
    1から81までの数で右図のように，
    魔方陣を作った。空欄を埋めよ。
    魔方陣･･･縦横斜めの数の和が等しい。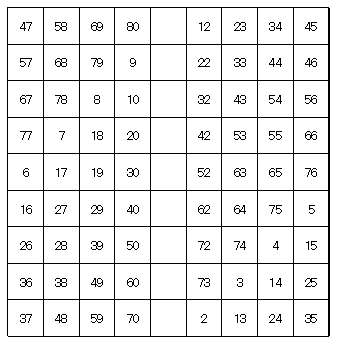

  49. （中学生向け）
    △ABCの辺CA上に点Dをとり，辺AB上に点Eを
    BE＝CDとなるようにとる。BC，DEの中点を
    それぞれM，N，直線MNと直線BA，CAとの交点
    をそれぞれF，Gとすると，△AFGは二等辺三角形
    となることを証明せよ。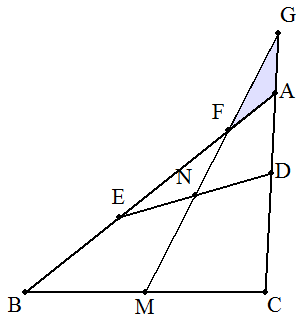

  50. 直径2cmの1円玉100枚を長方形の箱の中に重ならないように平らに敷き詰める。
    このとき，敷き詰める長方形の底面積を最小にするには，どのようなサイズの
    長方形に，どのように並べればよいか求めよ。ただし，長方形の縦横とも長さ
    はcm単位で整数値とする。