■趣味の数学問題集・Ａ問題
  1. （中学生向け）
    (1) ∠A＝30°である三角形ABCについて，
    頂点B，Cから対辺に下ろした垂線をそれぞれBD，CE
    とし，AB，ACの中点をそれぞれF，Gとするとき，
    DF⊥EGを証明せよ。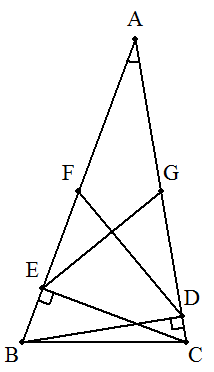
    (2) CA=b，AB=c，∠A＝30°である三角形ABCについて，
    頂点B，Cから対辺に下ろした垂線をそれぞれBD，CE
    とし，AB，ACの中点をそれぞれF，Gとするとき，
    四角形DEFGの面積を求めよ。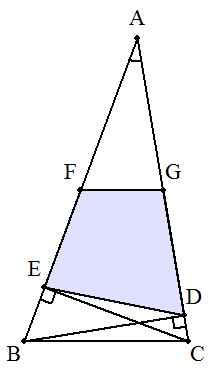
  2. （中学生向け）
    共有点をもたない円Oと線分STがある。
    STに垂直な円Oの直径ABの延長とSTとの交点をC，
    弧AB上に点Pをとり，PBの延長とSTとの交点をQとする。
    円OとAP，PCとの交点をそれぞれD，Eとするとき，
    △BDEは二等辺三角形となることを証明せよ。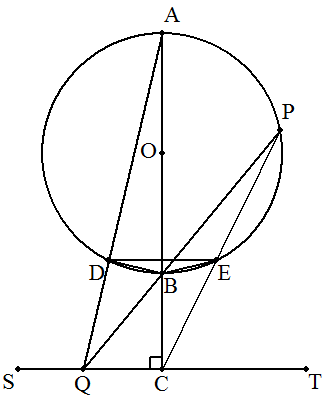
  3. （中学生向け）
    正方形ABCDのBC上に点Eを，CDの延長上に点Fをとる。
    次を証明せよ。
    (1)　BE＝DFのとき，∠AEF＝45°
    (2)　∠AEF＝45°のとき，BE＝DF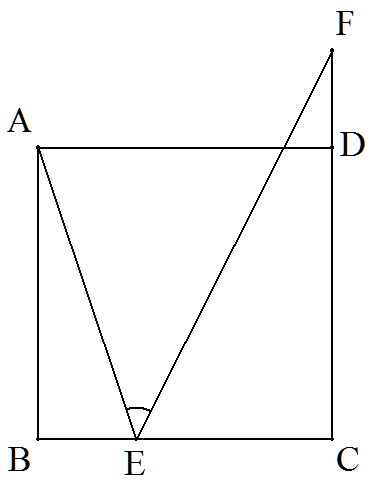


  4. 正三角形ABC内に3点D，E，Fを次のようにとる。
    Dは，AEを1：1に内分する点，
    Eは，BFを2：1に内分する点，
    Fは，CDを3：1に内分する点。
    このとき，
    (1)△DEF/△ABCを求めよ。（中学生向け）
    (2)△DEFの3辺の比を求めよ。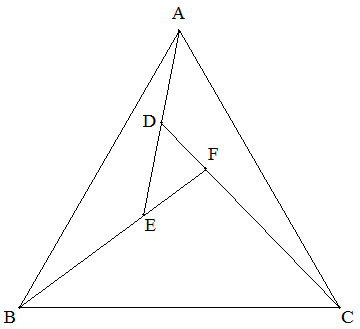

  5. （中学生向け）
    2円O1，O2の半径をそれぞれr1，r2とする。
    2円が外接しているとき，2円の共通接線で
    囲まれる三角形ABCの面積を求めよ。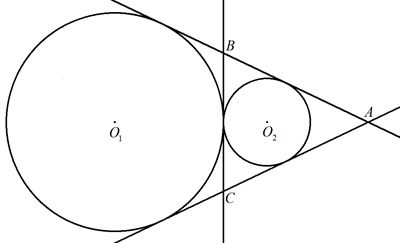


  6. 2円O1，O2の半径をそれぞれr1，r2とする。
    2円の中心間の距離がd（d>r1+r2）であるとき，
    2円の共通接線で囲まれる四角形ABCDの
    面積を求めよ。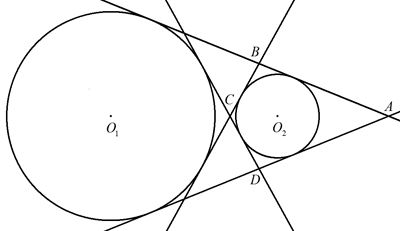


  7. 1辺の長さが1である正方形ABCDに，図のように
    4分の1円ABDとBCを直径とする半円が描かれて
    いる。
    斜線部分の面積を求めよ。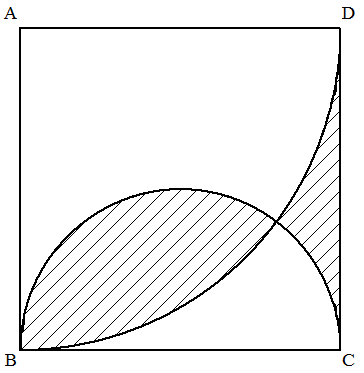


  8. 直径1の円に外接する正方形ABCD内に
    4分の1円ABDが描かれている。
    図の斜線部分の面積を求めよ。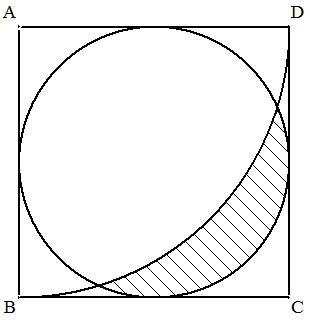


  9. （2017年に因んで）次の角度をそれぞれ求めよ。
    (1) ∠ADB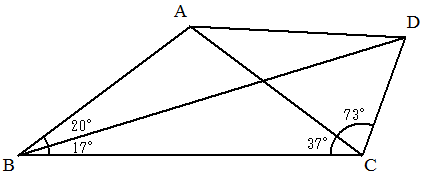
    (2) ∠BDC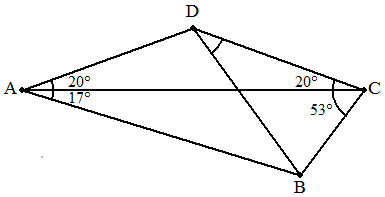



  10. 四角形ABCDについて，
    ∠ABD＝30°，
    ∠DBC=α，
    ∠ACB=30°，
    ∠DCA=2α-30°のとき，
    ∠ADBをαを用いて求めよ。
    ただし，15°＜α＜45°とする。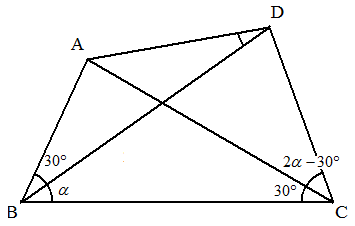


  11. 原点を通らない直線lは，2n本の直線
    y=(1/k)x　(k=1,2,3，…,2n)とそれぞれ，
    P1，P2，P3，…，P2n で交わっている。このとき，
    (P1P2/P2P3)×(P3P4/P4P5)×…×(P2n-1P2n/P2nP1)
    の値を求めよ。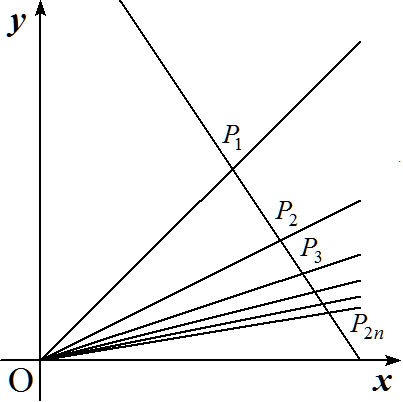


  12. 正三角形ABCの辺BC上に点Dをとり，△ABD，△ACDの
    内接円をそれぞれP(p)，Q(q)とおく。
    このとき，正三角形の1辺をp，qを用いて表せ。
    また，特にp=2，q=3のとき，正三角形の1辺を求めよ。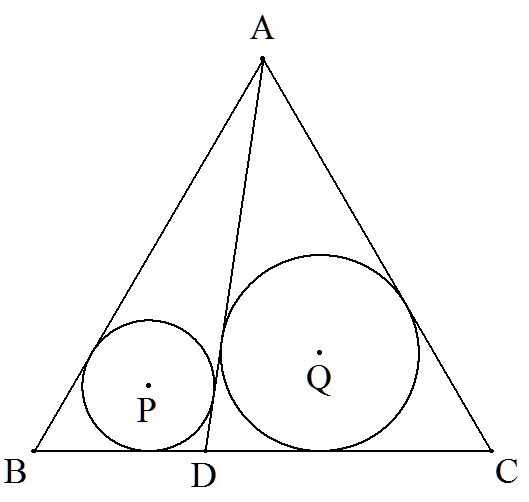


  13. 1辺の長さが1である正方形ABCDの辺BC，CD上に
    それぞれ点E，Fを∠EAF＝45°となるようにとる。
    △ABEと△ECFの内接円の半径が等しくなるとき，
    BEを求めよ。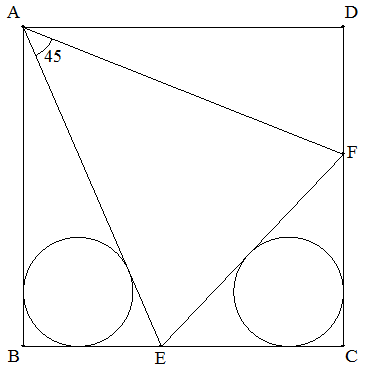


  14. 1辺の長さが1である正方形ABCDに，図のように
    内接する4円P，Q，R，Sの中心を頂点とするひし形に
    内接する円Tの半径を求めよ。
    ただし，円PとR，円QとSは等円とする。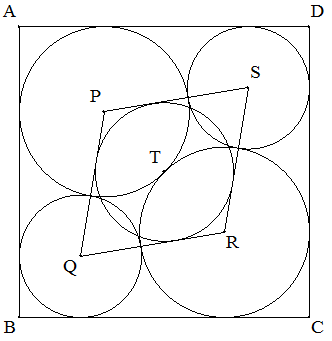



  15. 1辺の長さが1である正方形ABCDの内接円とB，Cを中心とする
    2つの扇形の重なった部分（斜線部分）の面積を求めよ。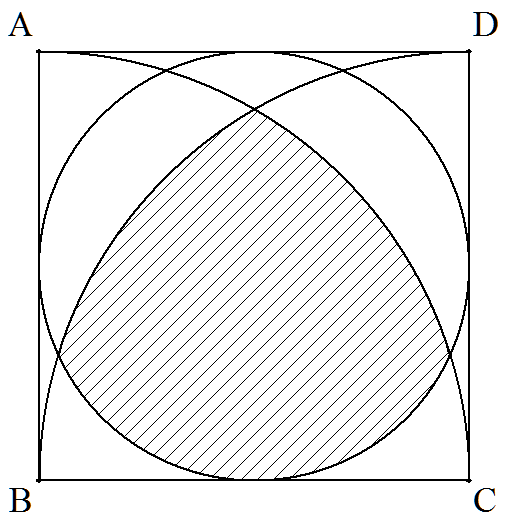



  16. 1辺aの正方形ABCDの辺DA上に点Eをとる。△ABE，△DECの
    内接円P，Qの半径がそれぞれ1，2であるとき，
    (1)aの値を満たす3次方程式を1つ求めよ。
    (2)△EBCの内接円Rの半径rの値を満たす3次方程式を1つ求めよ。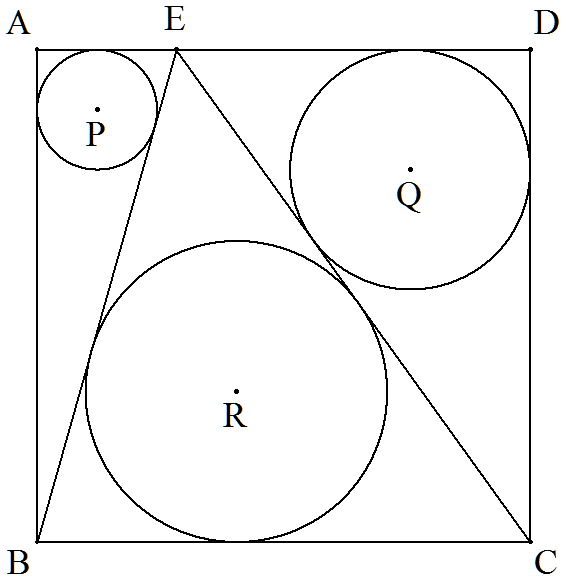


  17. （中学生向け）
    正方形ABCD内の点Iを通り，図のように
    直角を挟む2辺に平行な線分EF，GHを引く。
    長方形AGIEとIFCHの面積比が1：2である
    とき，∠FAH＝45°となることを証明せよ。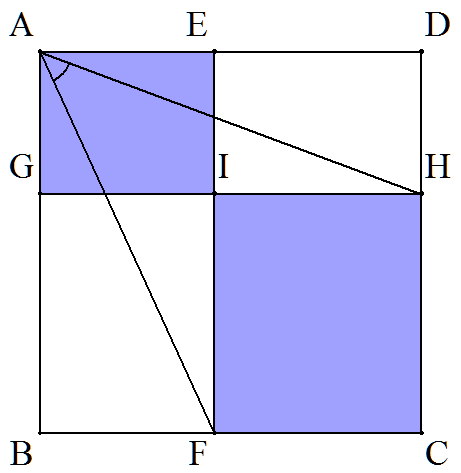


  18. （2017年8月，山形県天童市で作問）
    1辺の長さが1である正方形ABCDの4辺DA，
    AB，BC，CD上にそれぞれ点E，F，G，Hを，
    AE＝AF＝CG=CH＝1/3となるようにとる。
    図の八角形IJKLMNPQ（同じ大きさの将棋
    の駒2個の底を合わせた形）の面積を求めよ。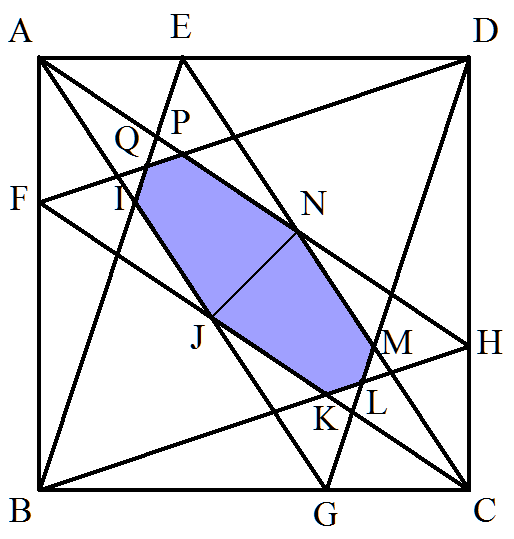



  19. 1辺の長さが1である正方形ABCD
    の辺DA，ABの中点をそれぞれ
    E，Fとする。BEとDF，BEとCF，
    CEとDFの交点をそれぞれG，H，I
    とする。四角形AFGE，GHCIの
    内接円P，Qの半径をそれぞれ求め
    よ。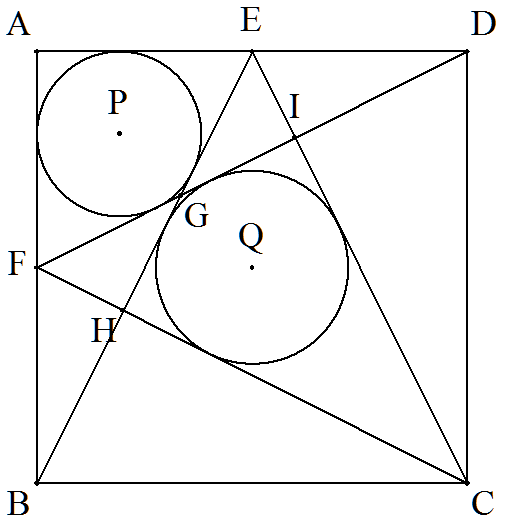



  20. BC=5，CA=4，AB=3である△ABCのBCの中点をDとする。
    CA，AB上にそれぞれ点E，Fを，AD，BE，CFで囲まれる
    三角形が正三角形になるようにとる。
    この正三角形の面積を求めよ。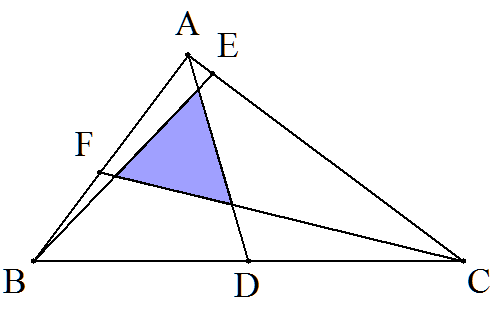



  21. 円内の点Ｐを通る2つの弦ＡＢ，ＣＤは垂直に交わっている。
    ただし，AP＜BP，CP＜DPである。AP＝a，BP＝b，CP＝cとおくとき，
    2つの斜線部分の面積（和）を求めよ。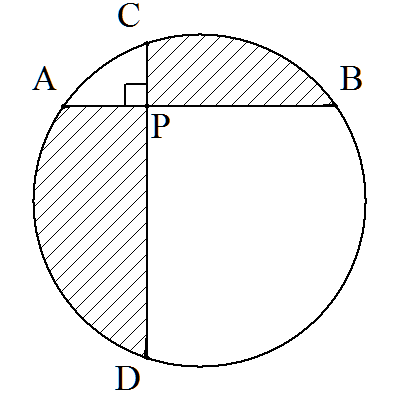



  22. (1) 右図の正八角形ABCDEFGH，台形ABGHの面積比が
    4：1となることを証明せよ。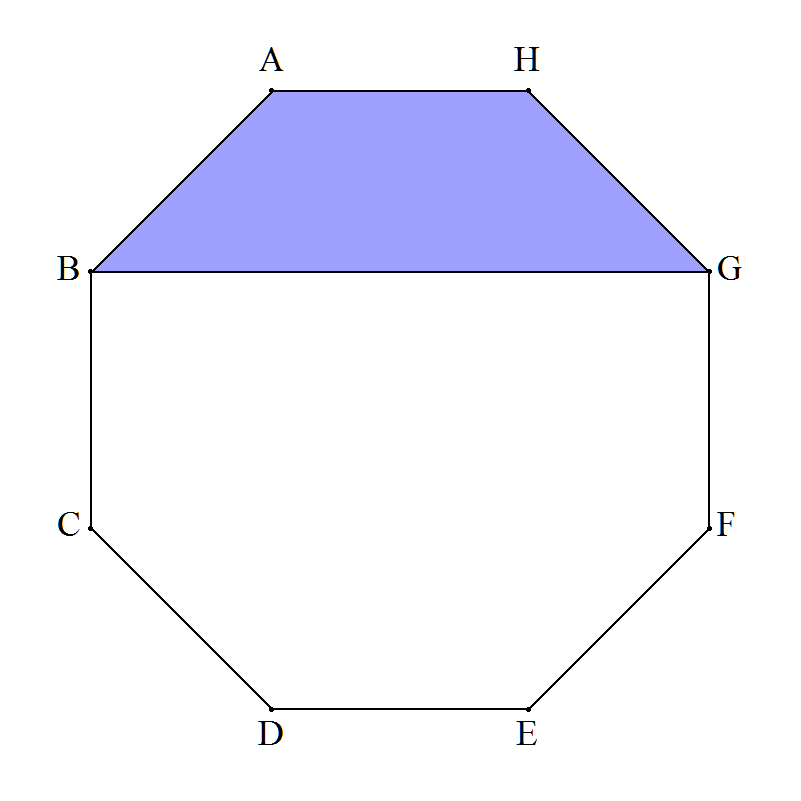
    (2) 右図の正九角形ABCDEFGHI，台形BCHIの面積比が
    3：1となることを証明せよ。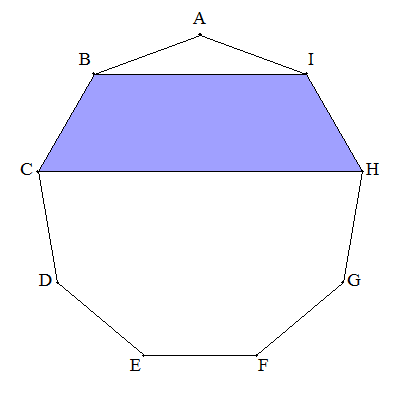
    (3) 右図の正12角形ABCDEFGHIJKL，台形ABKL，
    台形BCJKの面積比が12：1：3となることを
    証明せよ。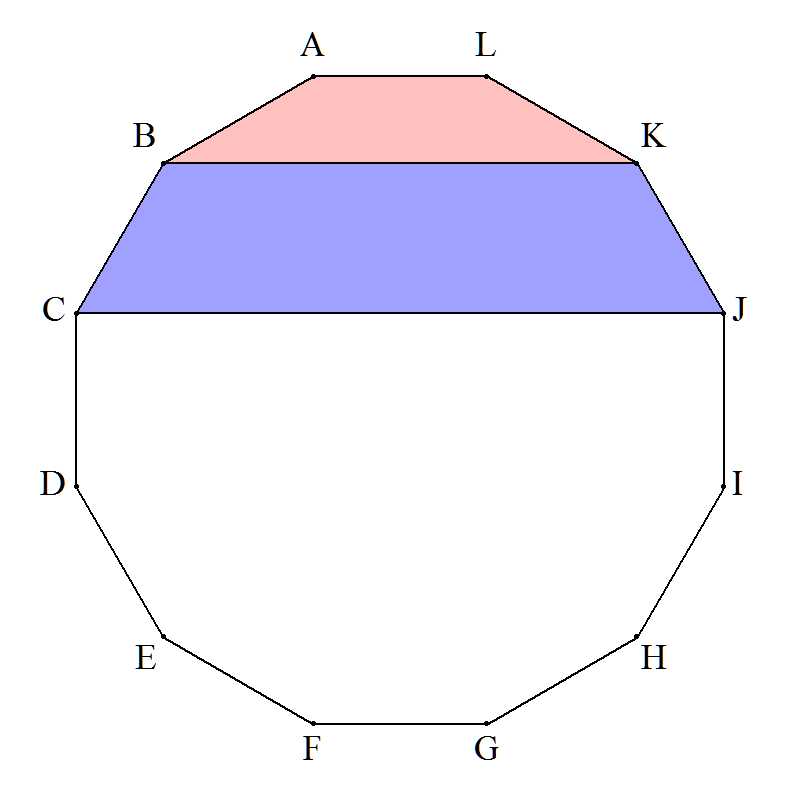



  23. 正九角形ABCDEFGHIの中心をO，BOとCIの交点を
    Jとする。∠OJH＝40°となることを証明せよ。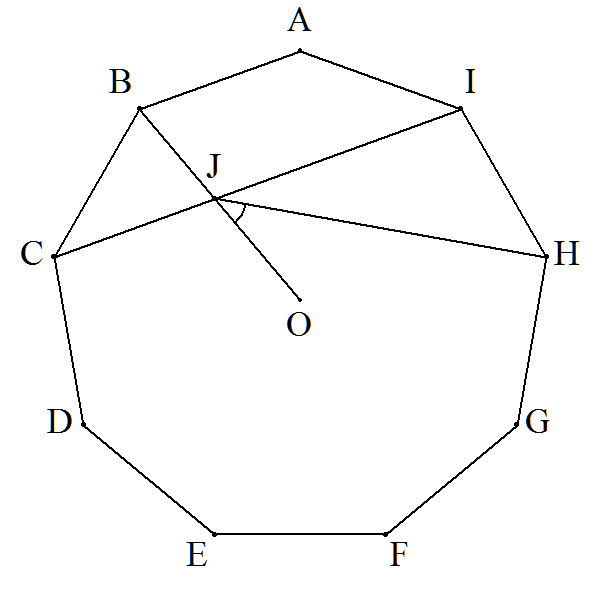



  24. A＝75°，B＝60°，C＝45°である△ABCの辺BC，CA，AB上にそれぞれ
    点D，E，Fを，∠DAB＝∠EBC=∠FCA＝15°となるようにとる。
    CF，ADの交点をP，AD，BEの交点をQ，BE，CFの交点をRとする。
    このとき，△PQR/△ABCの値を求めよ。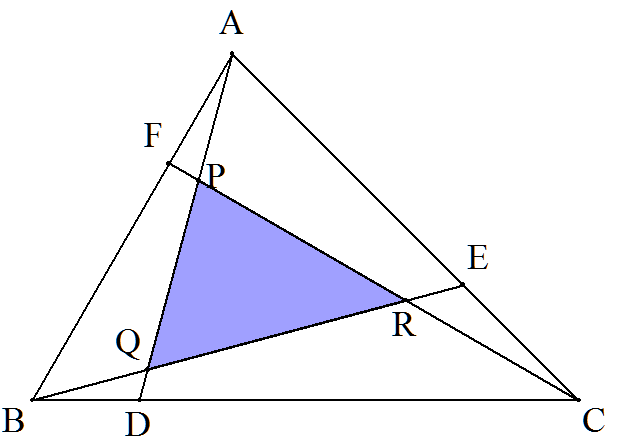



  25. △ABCの最大角AからBCに下した垂線の足をD，∠Bの二等分線と
    CAの交点をＥ，ABの中点をFとする。AD，BE，CFが1点で交わるとき，
    (1)　a＝15，c＝12のとき，bを求めよ。
    (2)　bをa，cを用いて表せ。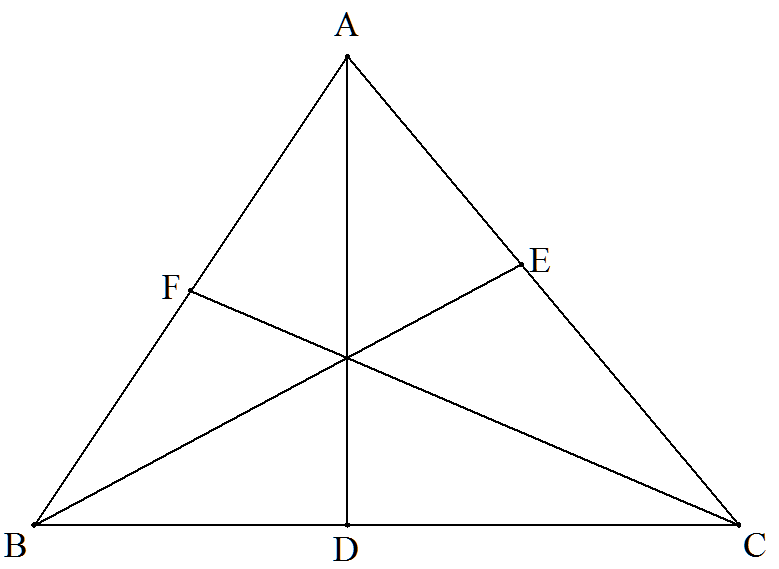



  26. △ABCのBC上にBに近い方から点D，Eを，∠BAD＝∠CAEとなるようにとる。
    3点A，D，Eを通る円とAB，ACとの交点をそれぞれF，Gとする。FG∥BCを
    証明せよ。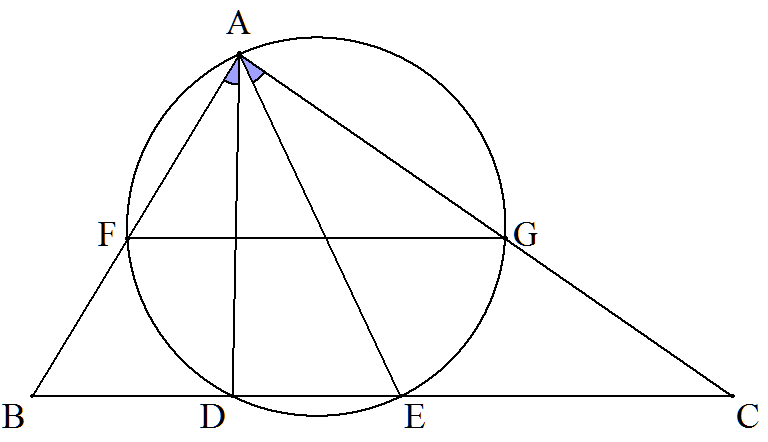



  27. 長方形ABCDは円に内接し，劣弧AD上に任意に点Pをとる。
    このとき，次の等式を証明せよ。
    △ABP＋△ADP＝△ACP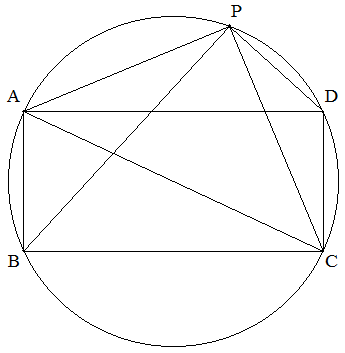



  28. △ABCのBCあるいはその延長上に2点D，Eを∠AEB＝∠ADC＝Aとなるようにとる。
    次を証明せよ。
    (1)　余弦定理　a2=b2+c2-2bccosA
    (2)　加法定理を用いず　sin2A=2sinAcosA
    (3)　加法定理を用いず　sin(A-B)/sin(A+B)=(a2-b2)/c2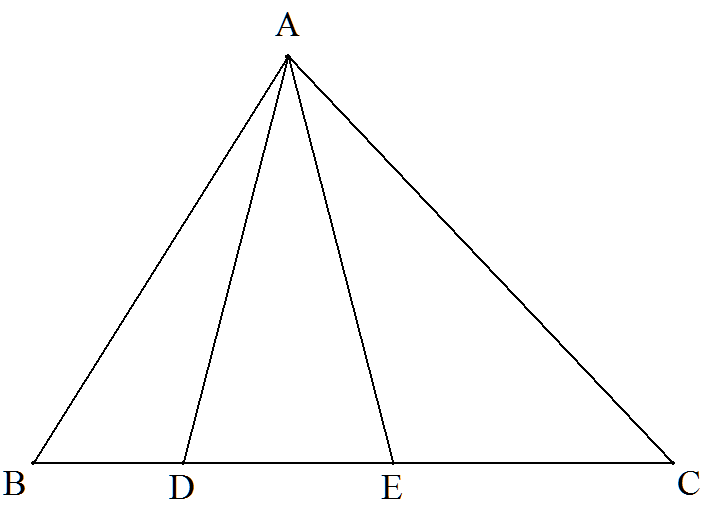



  29. 次の等式を証明せよ。
    (6a2-4ab+4b2)3=(3a2+5ab-5b2)3+(4a2-4ab+6b2)3+(5a2-5ab-3b2)3


  30. △ABCの3つの傍心を図のようにJ，K，Lとする。傍接円J，K，LとAB，BC，CAとの接点をそれぞれD，E，F，
    同様にCA，BC，CAとの接点をそれぞれP，Q，Rとする。このとき，次の値をそれぞれ求めよ。
    (1)　(△DEF-△ABC)/△ABC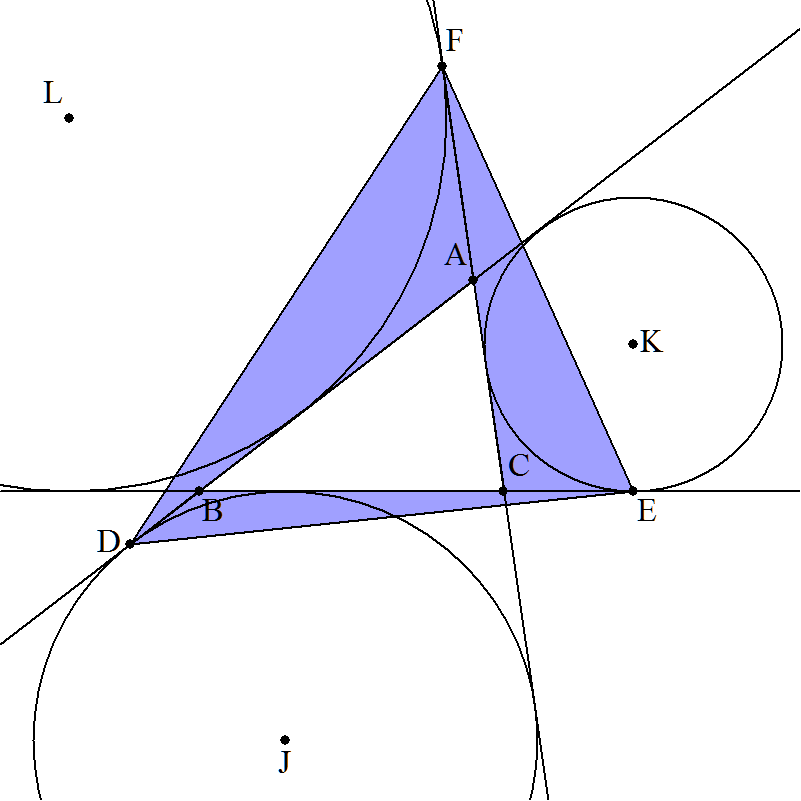
    		 (2)　(△PQR-△ABC)/△ABC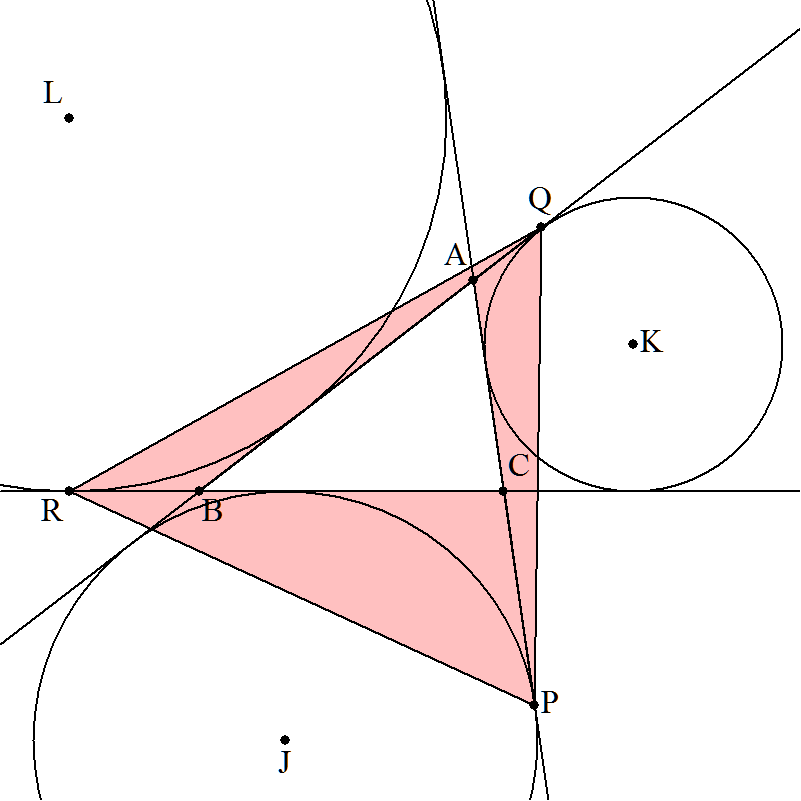



  31. MAKE2018
    1～9までの9個の数字をこの順に使い，四則演算記号，括弧，√などの記号を使って2018を作りなさい。
    （A169，A304の類題）




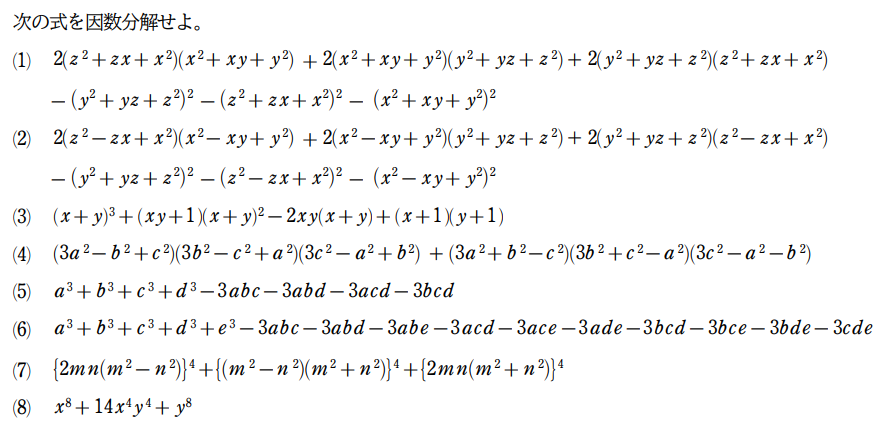
  33. △ABCの垂心をHとし，AH，BH，CHをそれぞれ延長し，△ABCの
    外接円との交点をそれぞれD，E，Fとする。また，ADとBC，
    BEとCA，CFとABとの交点をそれぞれL，M，Nとする。
    BC＝15，CA＝14，AB＝13のとき，△LMN/△DEFの値を求めよ。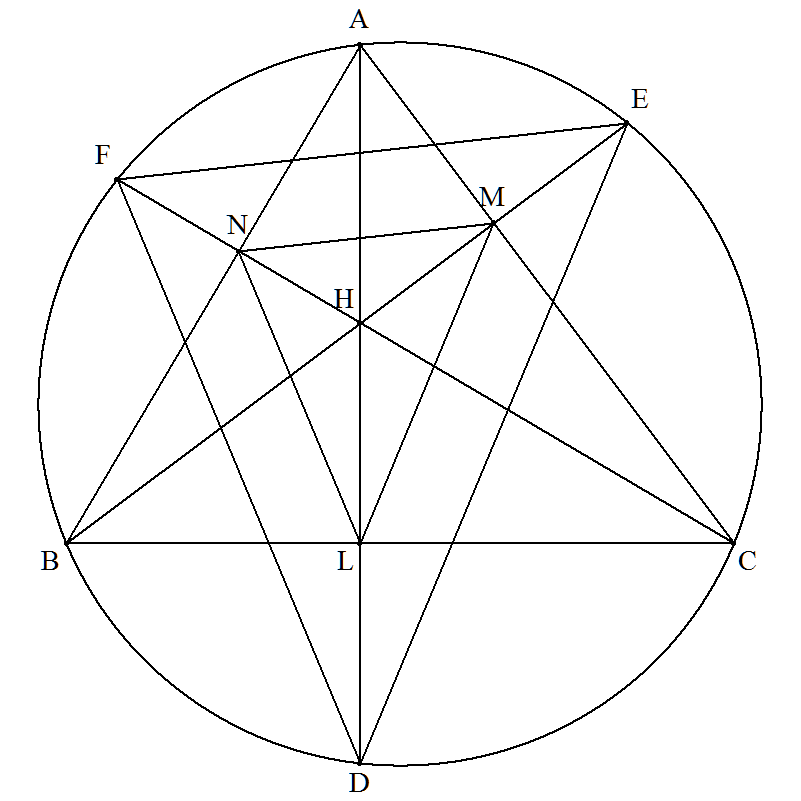



  34. △ABCの内心IからBC，CA，ABに下した垂線の足をそれぞれD，E，Fとする。
    また，AI，BI，CIをそれぞれ延長し，△ABCの外接円との交点をそれぞれ
    L，M，Nとする。このとき，△DEF：△LMN＝r2：R2となることを証明せよ。
    ただし，r，Rはそれぞれ△ABCの内接円，外接円の半径とする。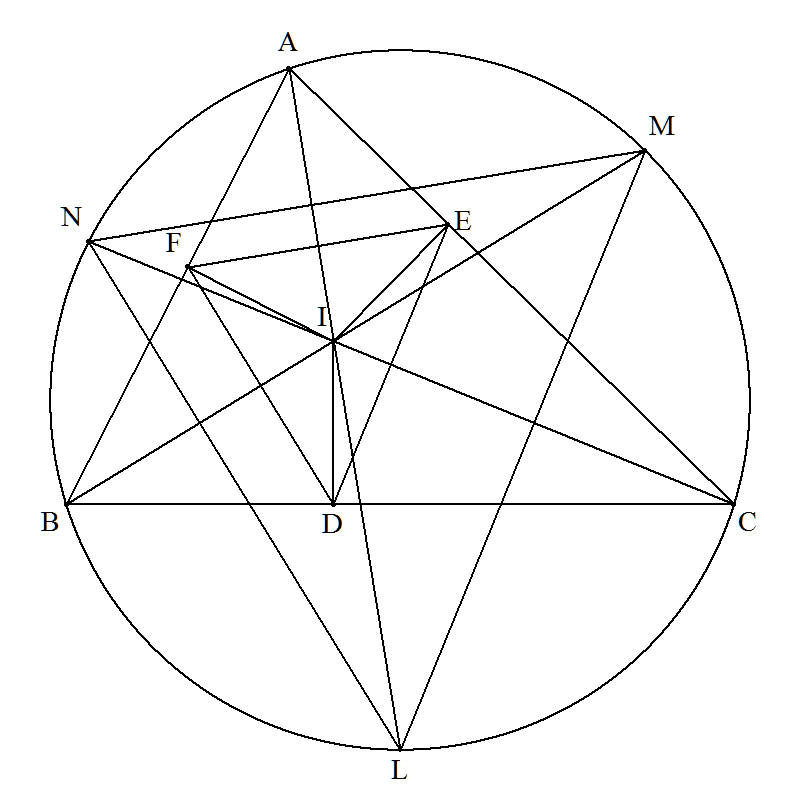



  35. (1)　x5-2x3+x-1=0の1つの解をαとする。
    　α2を解にもつ整数係数の5次方程式を1つ求めよ。
    (2)　x4-2x-1=0の1つの解をαとする。
    　α3を解にもつ整数係数の4次方程式を1つ求めよ。

  36. (1)
    立方体ABCD-EFGHについて，3点P，Q，RをそれぞれAB，AD，AE上にとる。
    また，Aから△PQRに下した垂線の足をSとする。
    AP＝p，AQ＝q，AR＝r，AS＝sとおくとき，次の等式を証明せよ。
    1/p2+1/q2+1/r2=1/s2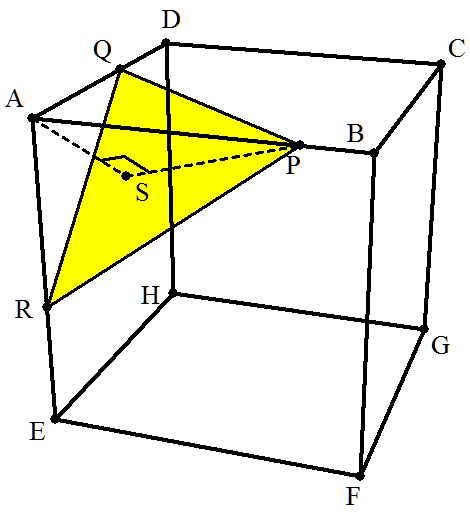
    (2)
    正四面体O-ABCについて，3点P，Q，RをそれぞれOA，OB，OC上にとる。
    また，Oから△PQRに下した垂線の足をSとする。
    OP＝p，OQ＝q，OR＝r，OS＝sとおくとき，次の等式を証明せよ。
    (3/2)( 1/p2+1/q2+1/r2)-(1/qr+1/rp+1/pq)=1/s2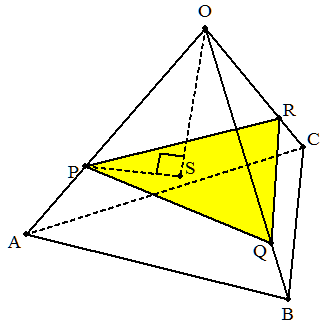



  37. m，nを負でない整数とする。
    5m+13nの形に表すことのできない整数の最大値を求めよ。


  38. すべての辺が等しい四角錐A-BCDEとその4辺AB，AC，AD，AEと
    交わる平面による切り口を図のように四角形PQRSとする。
    AP＝p，AQ＝q，AR＝r，AS＝sのとき，
    (1) 四角錐A-PQRSの体積を求めよ。
    (2) 1/p+1/r=1/q+1/s を証明せよ。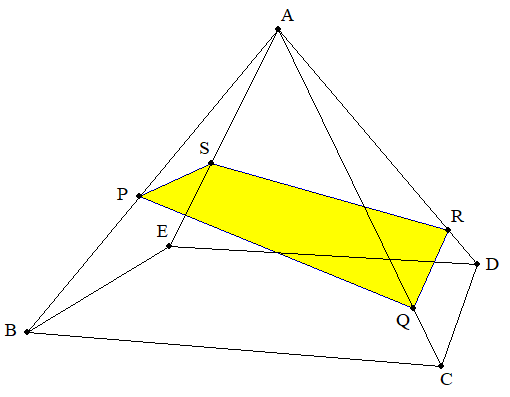



  39. △ABCにおいて，頂点から対辺に下した3つの垂線をそれぞれの角の二等分線に関して対称に折り返した3つの直線について
    (1)　1点で交わることを証明せよ。
    (2)　この点は△ABCのどのような点か。

  40. 22018の下3桁を求めよ。


  41. △ABCの外心、垂心をそれぞれO，Hとする。
    弧BCの中点をD，E（DはAと反対側）とし，
    BCに関する点Dの対称点をFとする。
    このとき，四角形AEFHは平行四辺形になる
    ことを証明せよ。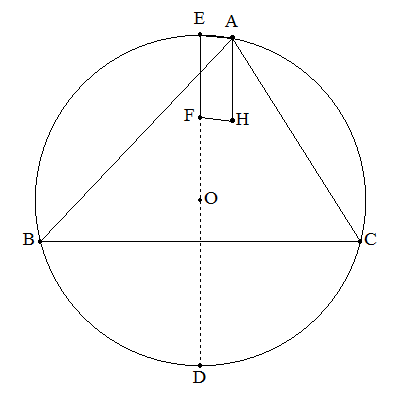



  42. 10桁の数9999999999の2乗を計算せよ。


  43. 次の分母を有理化せよ。
    (1)　1/(√2＋√3＋√5＋√7)
    (2)　1/(√2＋√3＋√5＋√7＋√11)

  44. （Fuhrmann円の性質）
    △ABCにおいて，頂点を含まない外接円の弧BC，CA，ABの中点をそれぞれ
    D1，D2，D3とし，辺BC，CA，ABに関するD1，D2，D3の対称点をそれぞれ
    P，Q，Rとする。
    △PQRの外接円は，△ABCの垂心HとNagel点Nを直径の両端とする円である
    ことを証明せよ。
    なお，三角形の辺と傍接円との接点と頂点をつなぐ3直線は1点で交わり，
    この点をNagel点という。また，△PQRの外接円を△ABCのFuhrmann円という。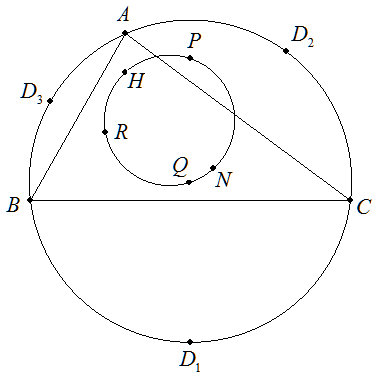



  45. △ABCにおいて、頂点を含まない外接円の弧BC，CA，ABの中点を
    それぞれD，E，Fとするとき，AD⊥EFを証明せよ。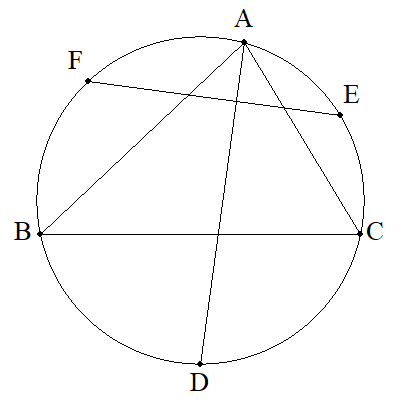



  46. f(x)は3次式で，f(1)=1/13，f(2)=1/23，f(3)=1/33，f(4)=1/43のとき、
    f(0)およびf(5)の値を求めよ。


  47. △ABCの内角をそれぞれA，B，C，△DEFの内角をそれぞれ
    D，E，Fとする。
    2つの三角形を図のように辺と辺が交わるように重ねた
    とき，交点G，H，I，J，K，Lが同一円周上にあった。
    HKとILの交点をMとするとき，∠HMLを2つの三角形の内角を
    用いて表せ。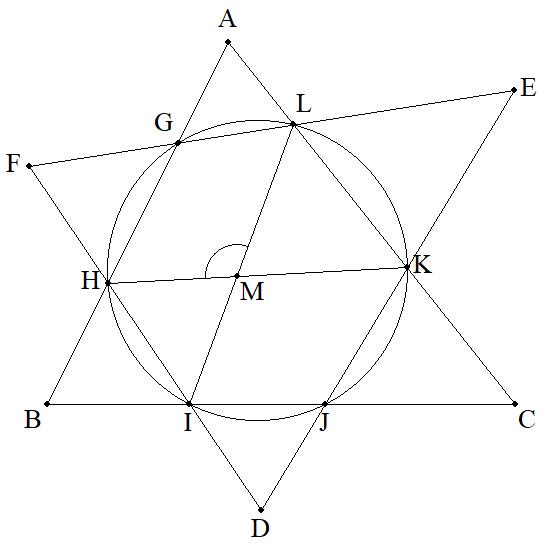



  48. 正三角形ABCを含む円と3辺の延長との交点を図のように
    D，E，F，G，H，Iとする。GDとFI，DIとEF，IFとHEとの交点を
    それぞれP，Q，Rとする。
    ∠DPI＝74°，∠FRE＝64°のとき，∠IQFを求めよ。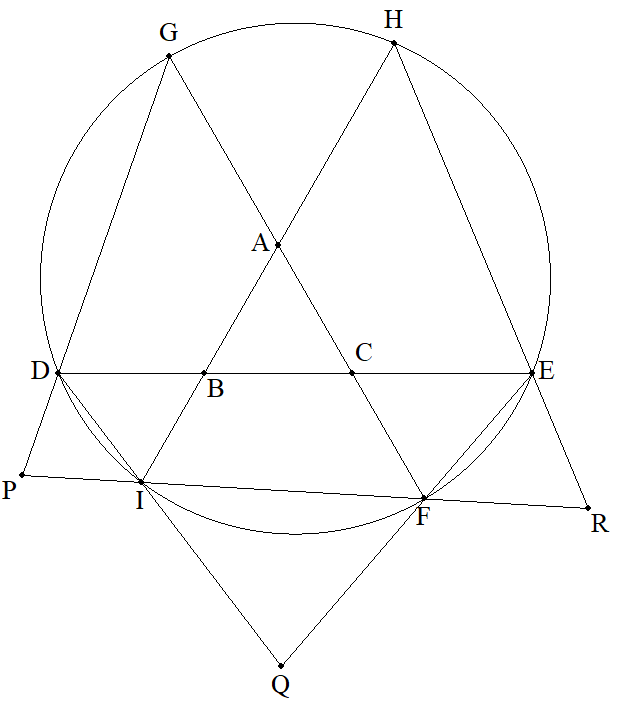



  49. CA=b，AB=c，b＜cである△ABCをAを中心にθだけ回転させる。
    このとき，B，Cの移動先をそれぞれD，Eとする。
    DE上にCがあるとき，
    (1)　回転角θを三角形の内角を用いて求めよ。
    (2)　△ACEの面積をｍとおくとき，△BDCの面積を，b，c，mを
    用いて表せ。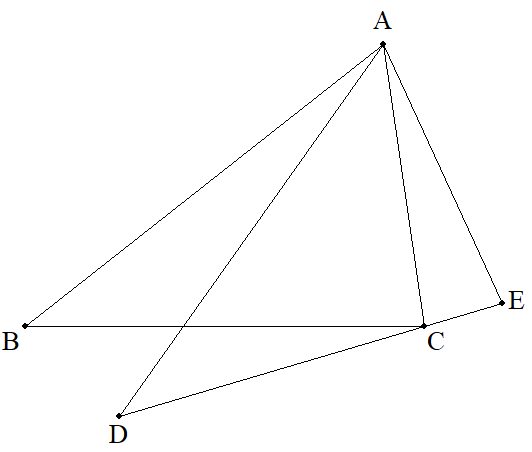



  50. 1辺の長さ1の正方形9個を図のように配置する。
    黄部の面積を求めよ。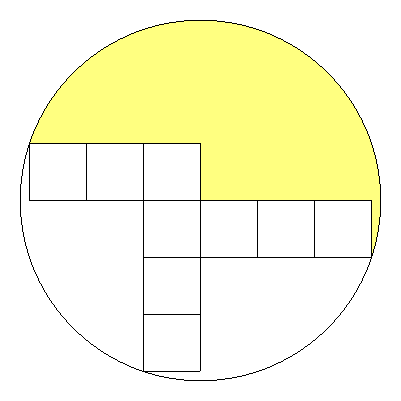