趣味の数学問題集・Ａ問題

■趣味の数学問題集・Ａ問題

x＞0，y＞0のとき，√(x²-6x+13)+√(x²+y²)+√(y²-8y+17)の最小値と，そのときのx，yの値を求めよ。

△ABCの外側に正方形BCDE，CAFG，ABHIを作る。DIとEF，
EFとGH，GHとDIとの交点をそれぞれP，Q，Rとする。
次の場合について，△PQRの面積を求めよ。
(1)　∠A＝90°，CA＝b，AB＝c
(2)　BC=15，CA=14，AB＝13
(3)　BC=a，CA=b，AB＝c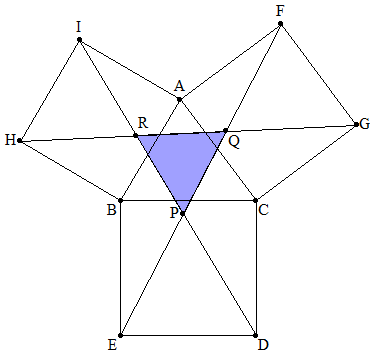

（Fuhrmann三角形の性質）

△ABCにおいて，頂点を含まない外接円の弧BC，CA，ABの
中点をそれぞれD₁，D₂，D₃とし，辺BC，CA，ABに関する
D₁，D₂，D₃の対称点をそれぞれP，Q，Rとする。
△D₁D₂D₃∽△PQRであることを証明せよ。
なお，△PQRを△ABCのFuhrmann三角形という。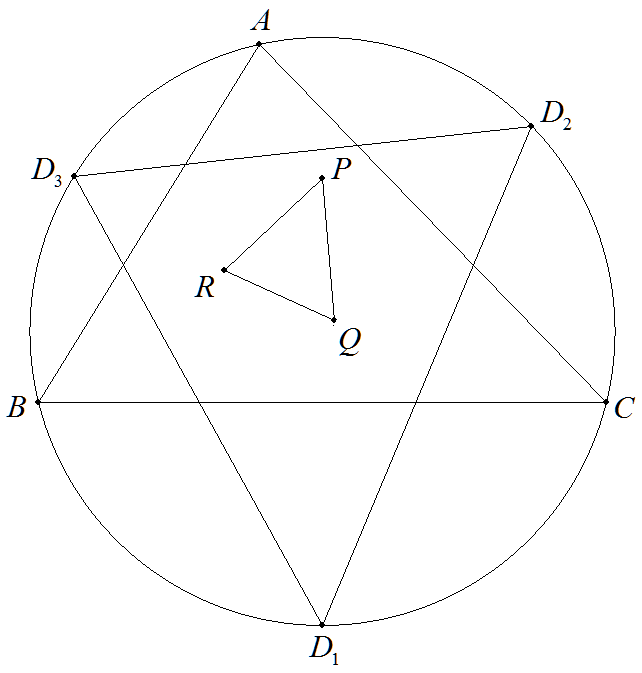

2円O₁，O₂の共通外接線ABと共通内接線EFの交点をPとする。
2円O₁，O₂の直径がそれぞれ，17，7で，O₁O₂＝13のとき，PBを
求めよ。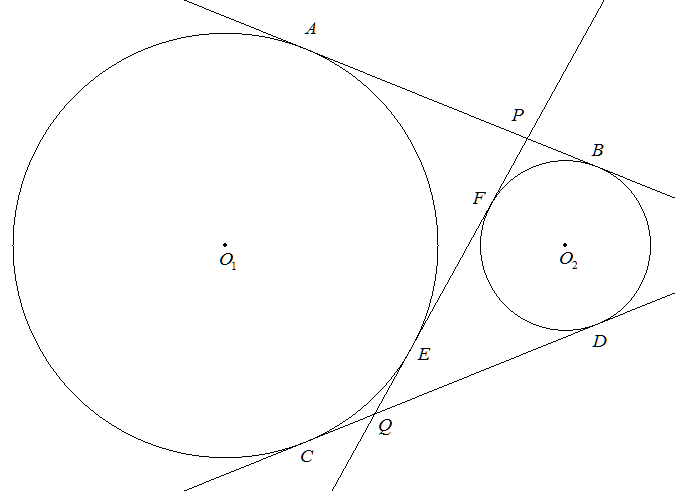
△ABCについてBCを1:k，CAを1:l，ABを1:mに内分す
る点をそれぞれD，E，Fとする。CFとDEの交点をPとし，
APとBCの交点をQとするとき，BQ：QCを求めよ。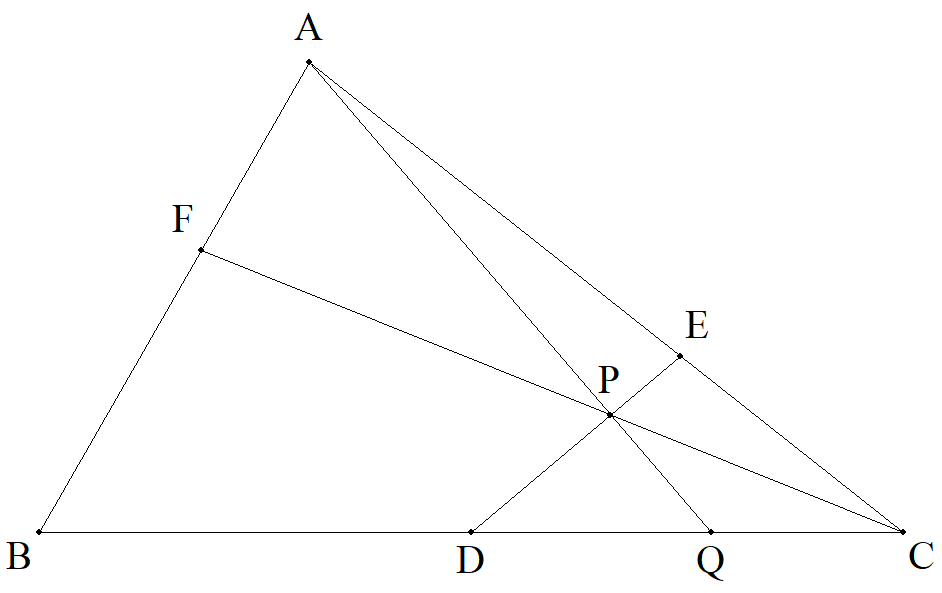
√2018ー√2019＋√(2018×2019)の整数部分を求めよ。
平行四辺形ABCDと1点Pがある。このとき，△PAB，△PBC，△PBDの3つの三角形について関係を求めよ。
ある本屋さんで次の様なキャンペーンが行われた。本を1冊買うたびにトランプのしおりが付いてくる。
そして1ペアがそろえば記念品がもらえるという。ジョーカーはなく，同じカード2枚でも1ペアとみなす。
記念品をもらうために買う本の冊数の期待値を求めよ。

四角形ABCDの対角線AC，BDの交点Oを通り，AB，DCに平行に引いた
直線とBCとの交点をそれぞれP，Qとするとき，BP²+CQ²=PQ²ならば，
DP，AQの中点M，NとOとは一直線上にあることを証明せよ。
（作：清宮俊雄）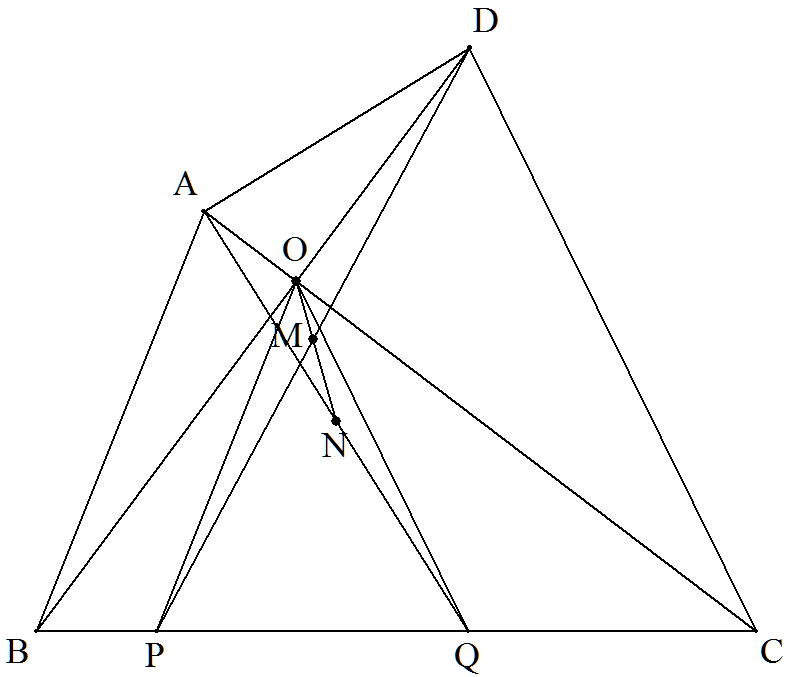

次の巡回分数式の値を求めよ。
(1)　(b+c)/a=(c+a)/b=(a+b)/c
(2)　b/a=c/b=a/c
(3)　(a+b)/c=(b+c)/d=(c+d)/a=(d+a)/b
(4)　(c+d)/(a+b)=(d+e)/(b+c)=(e+a)/(c+d)=(a+b)/(d+e)=(b+c)/(e+a)
1²⁰¹⁹+2²⁰¹⁹+3²⁰¹⁹+…+2019²⁰¹⁹を101で割ったときの余りを求めよ。

a=8，b=7，c=5である△ABCのBC上にBに近い方から2点D，Eをとる。
△ABD，△ADE，△AECの内接円の半径が等しくなるとき，その半径
およびBD，DE，ECをそれぞれ求めよ。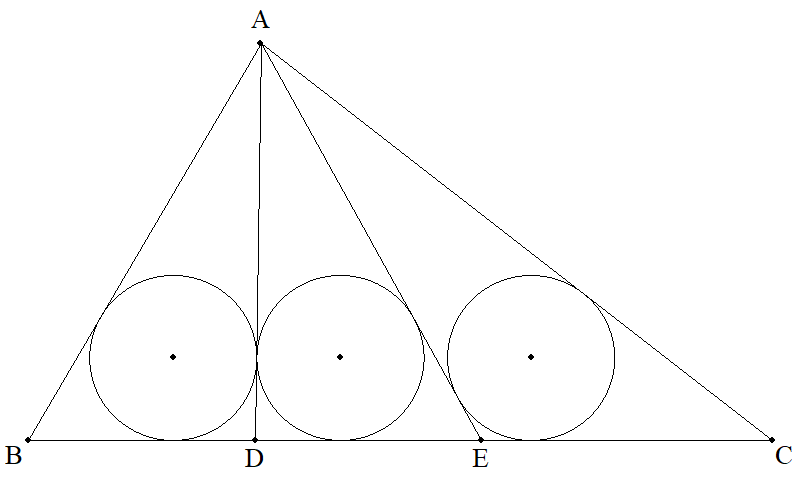

a=8，b=7，c=5である△ABCのBC上に点Dを，△ABDと
△ACDの内接円の半径が等しくなるようにとる。
次をそれぞれ求めよ。
(1)　BD
(2)　AD
(3)　等円の半径
(4)　BC＝a，CA＝b，AB＝c（b＞c）として，BDを求めよ。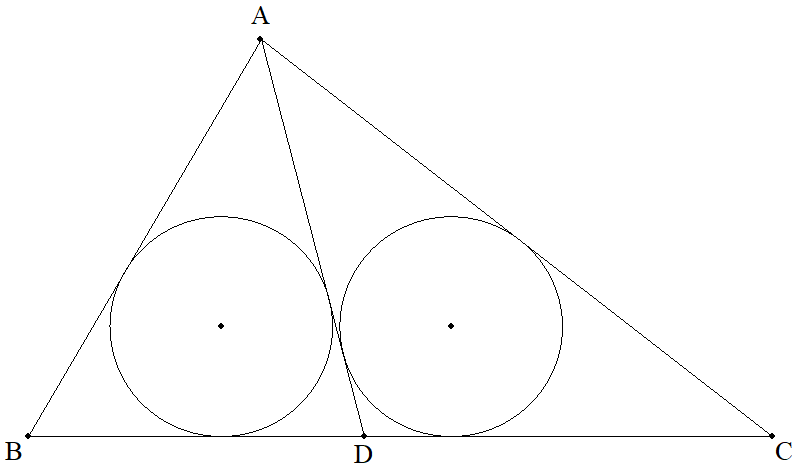

a＞0，ab-h²＞0のとき，x，yについての2次式 ax²+2hxy+by²+2gx+2fy+c の最小値を求めよ。
△ABCの垂心をHとする。AH＝a/tanAを証明せよ。
(1)　0＜a＜c，0＜b＜dのとき，√{(x-a)²+b²}+√{(x-c)²+d²}の最小値と，そのときのxの値を求めよ。
(2)　a＞b＞0のとき，√{(x-y)²+y²)}+√{(x-a)²+b²)}+√{(y-a)²+(y-b)²)}の最小値と，そのときのx，yの値を求めよ。
AB＝AD＝a，CB＝CD＝bである凧形四角形ABCDについて，
次の場合における内接円の半径を求めよ。
(1)　BD＝c
(2)　四角形は円に内接する
(3)　AC=c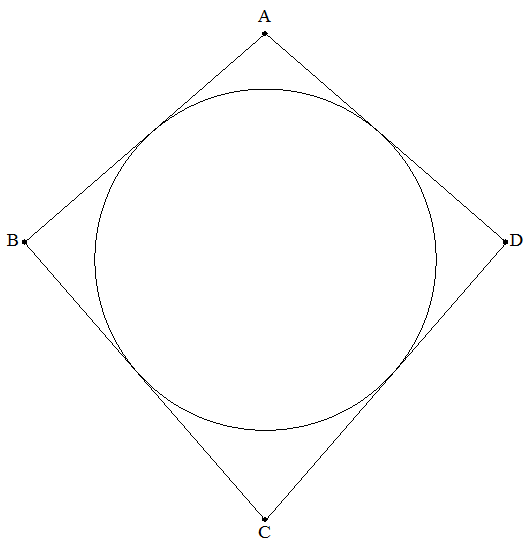
(1)
x₁+x₂+x₃=1，
x₁²+x₂²+x₃²=2，
x₁³+x₂³+x₃³=3のとき，
x₁⁴+x₂⁴+x₃⁴の値を求めよ。
(2)
x₁+x₂+x₃+x₄=1，
x₁²+x₂²+x₃²+x₄²=2，
x₁³+x₂³+x₃³+x₄³=3，
x₁⁴+x₂⁴+x₃⁴+x₄⁴=4のとき，
x₁⁵+x₂⁵+x₃⁵+x₄⁵の値を求めよ。
(3)
x₁+x₂+x₃+x₄+x₅=1，
x₁²+x₂²+x₃²+x₄²+x₅²=2，
x₁³+x₂³+x₃³+x₄³+x₅³=3，
x₁⁴+x₂⁴+x₃⁴+x₄⁴+x₅⁴=4，
x₁⁵+x₂⁵+x₃⁵+x₄⁵+x₅⁵=5のとき，
x₁⁶+x₂⁶+x₃⁶+x₄⁶+x₅⁶の値を求めよ。
(4)
x₁+x₂+x₃+x₄+x₅+x₆=1，
x₁²+x₂²+x₃²+x₄²+x₅²+x₆²=2，
x₁³+x₂³+x₃³+x₄³+x₅³+x₆³=3，
x₁⁴+x₂⁴+x₃⁴+x₄⁴+x₅⁴+x₆⁴=4，
x₁⁵+x₂⁵+x₃⁵+x₄⁵+x₅⁵+x₆⁵=5，
x₁⁶+x₂⁶+x₃⁶+x₄⁶+x₅⁶+x₆⁶=6のとき，
x₁⁷+x₂⁷+x₃⁷+x₄⁷+x₅⁷+x₆⁷の値を求めよ。

△ABCにおいて，
CAの4等分点をCに近い方からD，E，F，
ABの3等分点をAに近い方からG，Hとする。
CHとBF，BE，BDの交点をそれぞれI，J，K，
CGとBD，BE，BFの交点をそれぞれL，M，N
とする。このとき，
(1)　四角形IJMN：四角形JKLMを求めよ。
(2)　△ABC＝1のとき，四角形IJMNと四角形
　JKLMの面積を求めよ。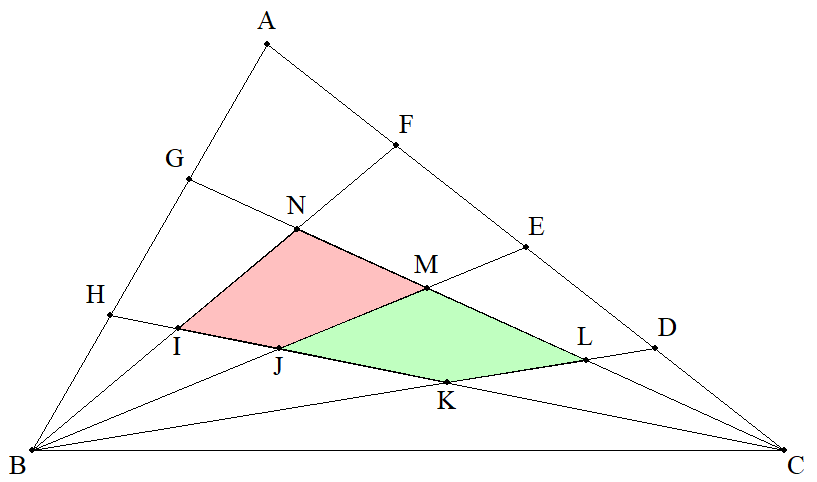

MAKE2019
1～9までの数字をこの順に使って，答が2019になる式を作れ。
使用できる記号は，＋，－，×，÷だけで，括弧は使えない。
ただし，12のように数字をつなげてもかまわない。
nは3以上の整数で，n個の実数x₁，x₂，…，x_nは次の2つの等式を満たしている。
x₁+x₂+…+x_n=a
x₁²+x₂²+…+x_n²=b
次の問いに答えよ。
(1)　n=3のとき，a，bの条件とx₁の値の範囲を求めよ。
(2)　n=4のとき，a，bの条件とx₁の値の範囲を求めよ。
(3)　n=5のとき，a，bの条件とx₁の値の範囲を求めよ。

AD∥BCである台形ABCDの対角線の交点をEとする。
線分FGはEを通りADに平行で，
台形AHID∽台形HBCI，
台形AJKD=台形JBCKとする。
AB＝a，BC=b，CD＝c，DA=d（d＜b＜a+c+d）のとき，
(1)　AF：FB，FGをそれぞれ求めよ。
(2)　AH：HB，HIをそれぞれ求めよ。
(3)　AJ：JB，JKをそれぞれ求めよ。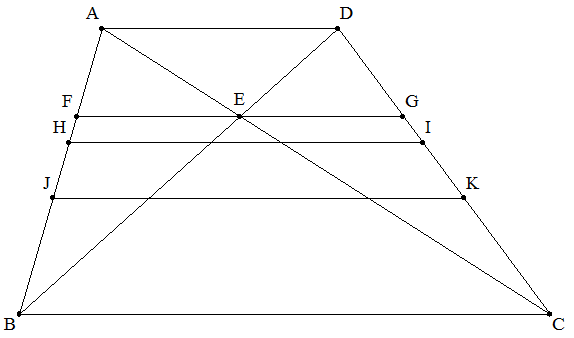

△ABCについて，BC上の点DでBCに接し，点Aを通る円の半径をr₁とする。
(1)　AD＝d，AからBCに下ろした垂線の足をHとし，AH＝hのとき，r₁を
d，hを用いて表せ。
(2)　BC=a，CA＝b，AB＝c，BD＝a₁，DC＝a₂，△ABC＝Sのとき，r₁を
a，b，c，a₁，a₂，Sを用いて表せ。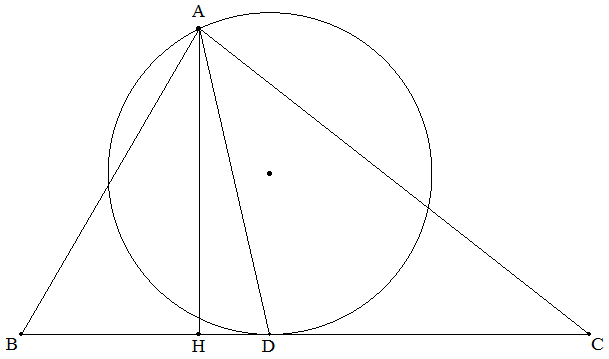

△ABCの3つの中線の長さが3，4，5のとき，
△ABCの面積を求めよ。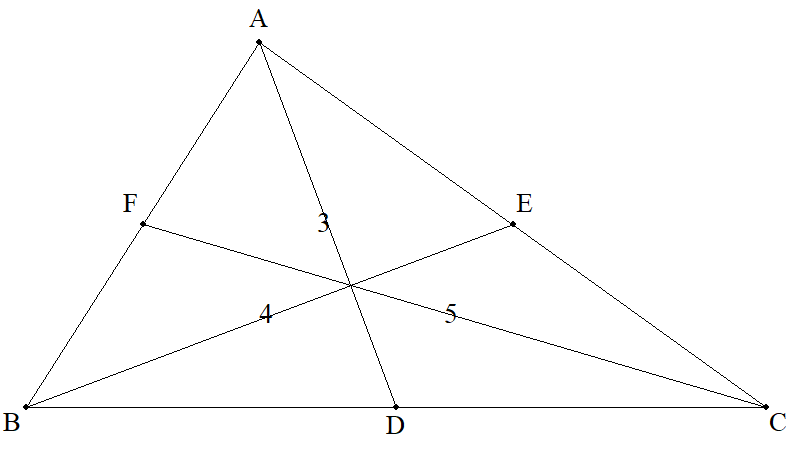
BC：CA：AB＝5：4：3である△ABC内に点Pを，
AP＝1，BP＝2，CP=3となるようにとる。
このとき，BCを求めよ。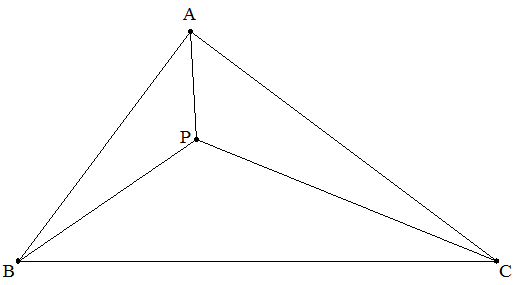
△ABCの3つの頂点から対辺までの長さが
4，5，6のとき，△ABCの面積を求めよ。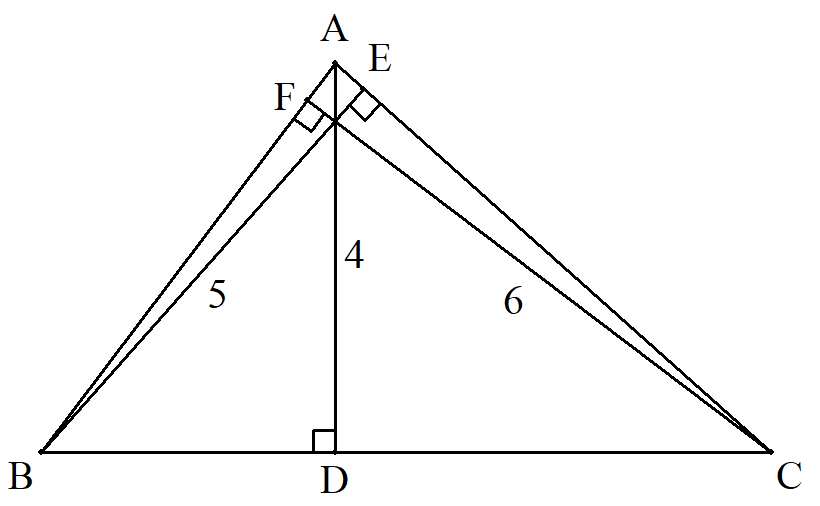
△ABCのCA上に点Dをとり，ABの中点をE，BD
とCEの交点をF，AFとDEの交点をGとする。
△EBF＝△AGDのとき，DA/CDの値を求めよ。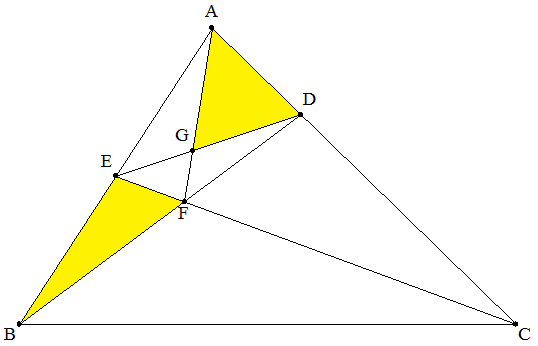
(1)　正17角形の対角線の交点のうち，頂点を除く個数を求めよ。
(2)　正18角形の対角線の交点のうち，頂点を除く個数を求めよ。
次の等式を証明せよ。
a³/(a-b)(a-c)(a-d)+b³/(b-c)(b-d)(b-a)+c³/(c-d)(c-a)(c-b)+d³/(d-a)(d-b)(d-c)=1

(1)　2つの放物線y=2x²+3x+4 ･･･①，
y=x²+x+1 ･･･② について，x=0における
①，②の接線をl₁，l₂，①，②とy軸との交点を
C₁，C₂とする。l₁，l₂の交点PとC₁，C₂を2：1に
外分する点Qを通る直線PQの方程式を求めよ。
(2)　2つの放物線y=a₁x²+b₁x+c₁ ･･･①，
y=a₂x²+b₂x+c₂ ･･･② （a₁≠a₂，b₁≠b₂，c₁≠c₂）
について，x=0における①，②の接線を
l₁，l₂，①，②とy軸との交点をC₁，C₂とする。
l₁，l₂の交点PとC₁，C₂をa₁：a₂に外分する点Qを
通る直線の方程式を求めよ。
(3)　(2)で，①，②からx²の項を消去した
方程式を求めよ。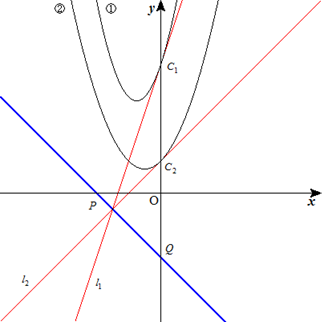

（中学生レベル）
中心角90°の扇形ABCの点Cを頂点として∠BCD＝30°になるように
直角三角形CDEを作る。ADの長さがCDの長さより20cm長くなるとき，
網掛けの部分の面積を求めよ。ただし，円周率はπとする。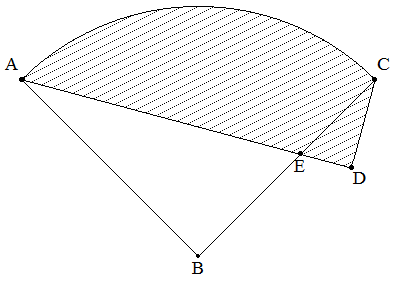

13個の半径1の円A，B，C，…，Mは次のように線分
RO，OP，PQで囲まれた部分に配置されている。
（RO⊥OP，OP⊥PQ）
また，6＜OP＜8 とする。
円Aは，OP，ORに接している。
円Cは，OP，PQに接している。
円Bは，OPに接し，2円A，Cの間に任意にある。
ただし，その隙間は0と2√3-2の間とする。
円Dは，4円F，A，B，Gに接している。
円Eは，4円G，B，C，Hに接している。
円Fは，ORに接し，2円I，Dに接している。
円Gは，4円I，D，E，Jに接している。
円Hは，PQに接し，2円I，Dに接している。
円Iは，4円K，F，G，Lに接している。
円Jは，4円L，G，H，Mに接している。
円Kは，ORに接し，円Iに接している。
円Lは，2円I，Jに接している。
円Mは，PQに接し，円Jに接している。
このとき，3円K，L，MはOPに平行な共通接線をもつ
ことを証明せよ。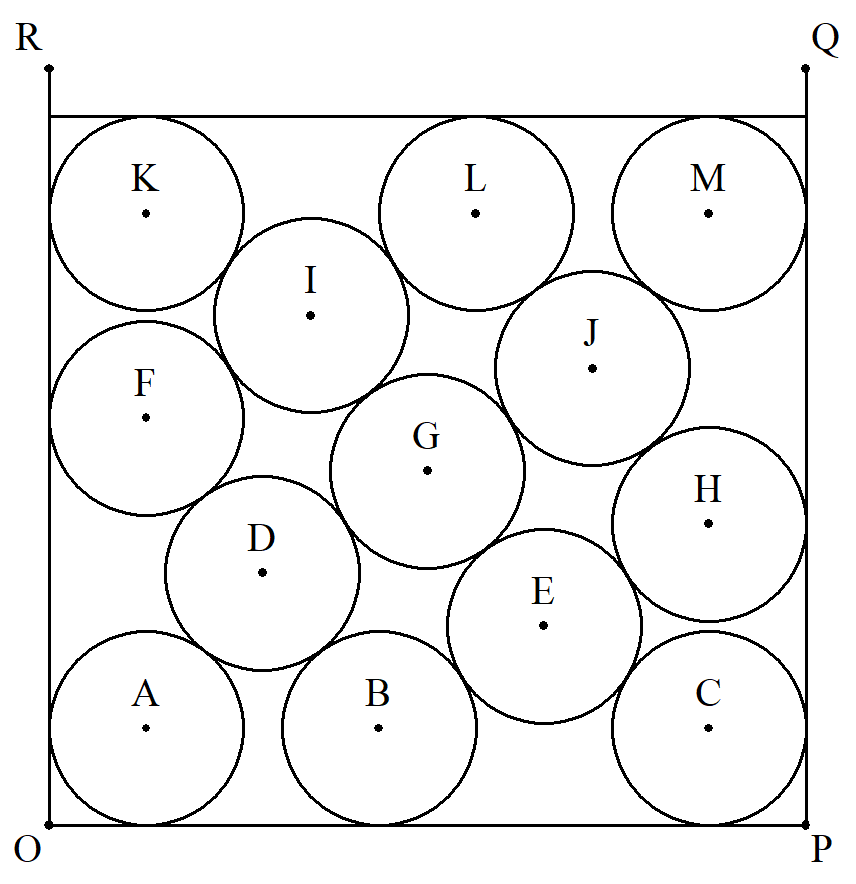

（中学生レベル）
4つの半径rの円の中心は正方形をなしている。
また，B，Dは2円の接点である。
四角形ABCDはAC＝4r，BD＝2rのひし形である。
このとき，図の網掛けの部分の面積を求めよ。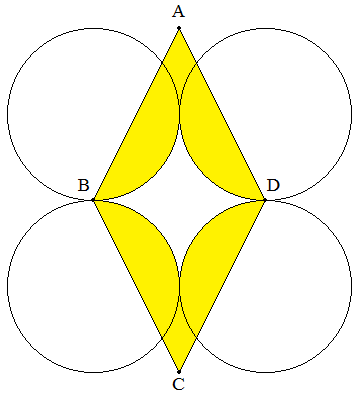

4次方程式x⁴+24x³+kx²-1452x+2020=0について，4つの解のうち，
2つの解の積が-20であるとき，次の問いに答えよ。
(1)　実定数kの値を求めよ。
(2)　方程式を解け。
次の問いに答えよ。
(1)　連続する4つの自然数の積について，平方数となることはあるか。あれば，
　　そのような数の中で最小となる数を求めよ。なければ理由を述べよ。
(2)　連続する4つの正の奇数の積は，平方数の差の形に変形できることを証明せよ。
Zを整数の集合とする。
集合A=｛a²+b²+c²+d²｜a，b，c，d∈Z｝は，積の演算について閉じていることを証明せよ。
△ABCの外側に，3点D，E，Fを△DCB∽△EAC∽△FBAとなるようにとる。
このとき，△AFE＋△DCB＝△BDF＋△EAC＝△CED＋△FBAを証明せよ。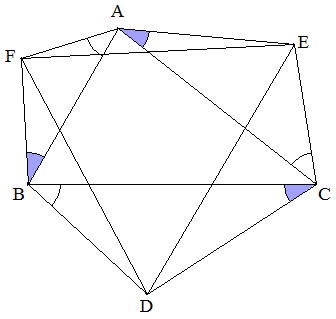

左図の1辺2の正三角形ABCを，DE，FG，HIで切断し，
四角形FBEGをFの周りに－180°回転して四角形FASLをつくり，
三角形DECをDの周りに180°回転して三角形DNAをつくり，
さらに三角形PMNをPの周りに180°回転して三角形PRSをつくる。
このとき，四角形GMRLが正方形になるとき，BEを求めよ。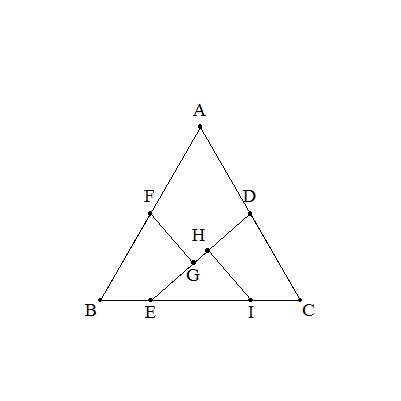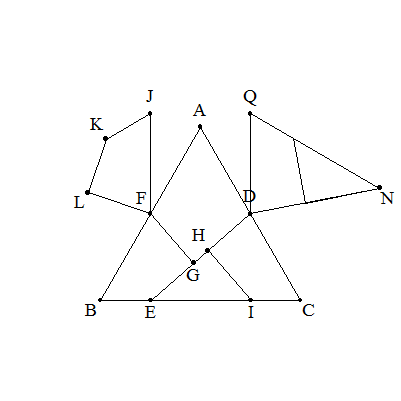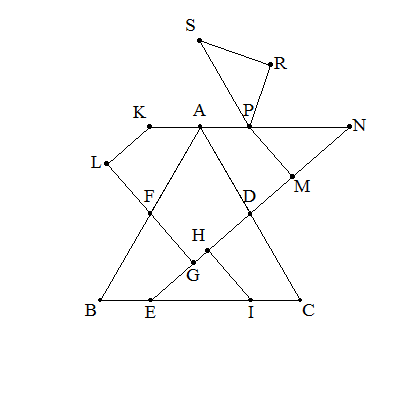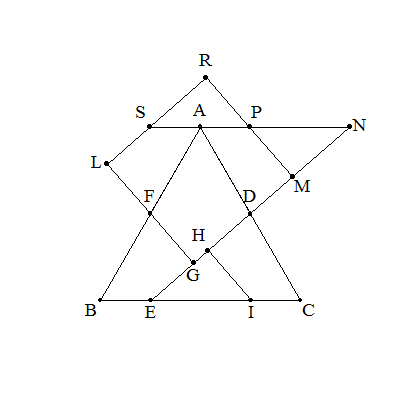

∠C＝90°の直角三角形ABCのAB上に点Dをとり，DからBC，CAに
下ろした垂線の足をそれぞれE，Fとする。
AF＝p，BE＝qとおくとき，長方形DECFの面積を求めよ。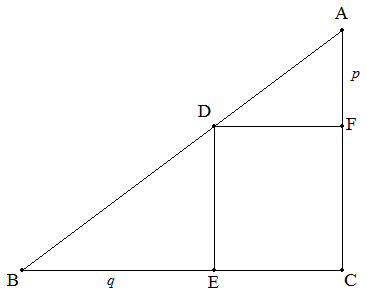

∠A＝90°の直角三角形ABCの内接円とBCとの接点をDとする。
BD＝a₁，DC＝a₂とおくとき，△ABCの面積を求めよ。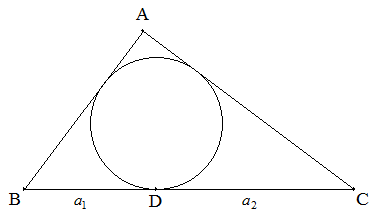
∠C＝90°の△ABCの内接円とABの接点DからBC，CAに下ろした
垂線の足をそれぞれE，Fとする。
AD=p，DB＝qとおくとき，長方形DECFの面積を求めよ。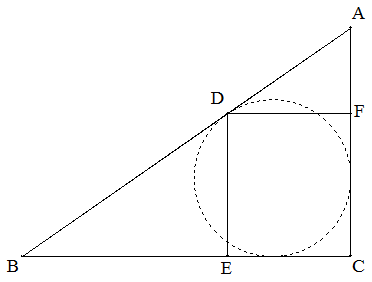
∠C＝90°の△ABCの内接円とABの接点DからBC，CAに
下ろした垂線の足をそれぞれE，Fとする。
AD＝p，DB＝qのとき，2つの弓形の面積の和を求めよ。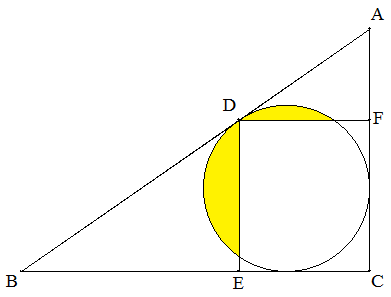

∠A＝90°，CA＝12，AB=5である△ABCの内心をP，頂点Aから
BCに下した垂線の足をD，BPとCA，ADとの交点をそれぞれE，R，
CPとAB，ADとの交点をそれぞれF，Qとする。
(1)　△PQRの外接円の半径を求めよ。
(2)　△PQRの面積を求めよ。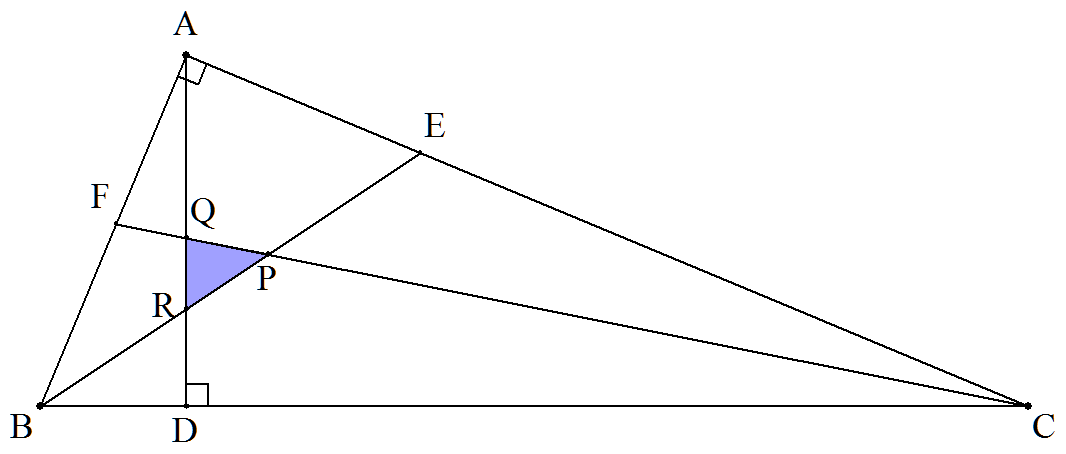

∠A＝90°，∠B＝53°である△ABCについて，AからBCに下した
垂線の足をD，△ABD，△ACDの内接円のBCでない共通外接線と
AC，AD，AB，CBとの交点を図のようにそれぞれE，F，G，Hとする。
このとき，∠GHBの大きさを求めよ。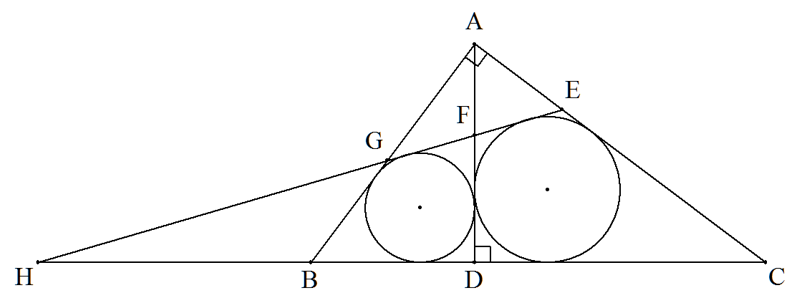

△ABCのBC，CA，AB上にそれぞれ点D，E，Fを，点FはDEに関して点Cと対称で，
∠AFE＝∠Cとなるようにとる。
このとき，
(1)　△AFE＝△EDCとなる△ABCの形状を答よ。
(2)　定規とコンパスを使って，(1)の条件を満たす△ABCと，△DEFを作図せよ。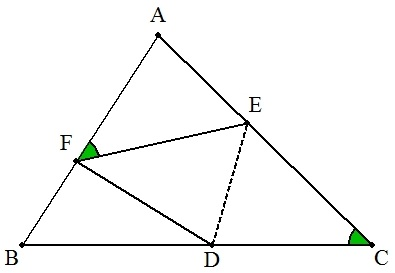

∠A＝90°である△ABCの頂点AからBCに下した垂線の足をD，△ABD，△ADCの
内接円の共通外接線のうちBC以外とCA，ABとの交点をそれぞれE，Fとする。
また，△ABD，△ACD，△AEFの内接円の半径をそれぞれr₁，r₂，r₃とするとき，
次の等式を証明せよ。
r₁r₂/r₃=(1/2)AD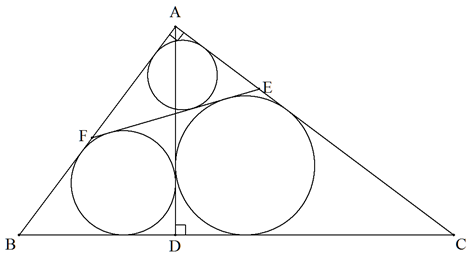

∠A=90°，CA＝4，AB＝3である△ABCにおいて，図のように辺に接する2つの
円P，Qは互いに外接している。2つの円の共通外接線のうちBCでない方と
CA，ABとの交点をそれぞれD，Eとする。
∠AED＝∠ACBのとき，DEを求めよ。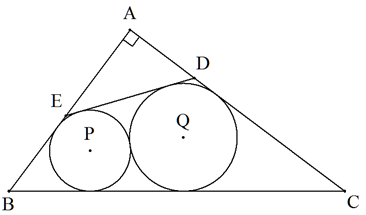

AD∥BC，AD＜BCである等脚台形ABCDに，図のように小円と大円が3辺に
接している。2円の共通内接線とAB，CDとの交点をそれぞれE，Fとする。
AD＝a，BC＝b，EF＝c （c²≧ab）とおくとき，次の問いに答えよ。
(1)　等脚台形ABCDの面積Sを求めよ。
(2)　小円の直径r，大円の直径Rをそれぞれ求めよ。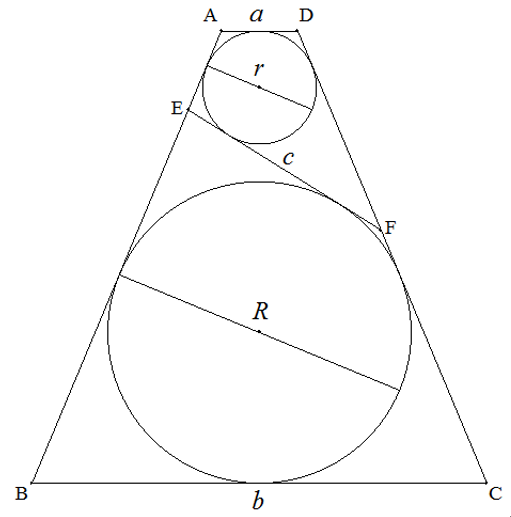

AD∥BCである等脚台形ABCD （AD＝a，BC=b，a＜b）に図のように大円，小円が
互いに外接し内接している。
このとき，次の問に答えよ。
(1)　台形ABCDの面積を求めよ。
(2)　小円，大円の直径r，Rをそれぞれ求めよ。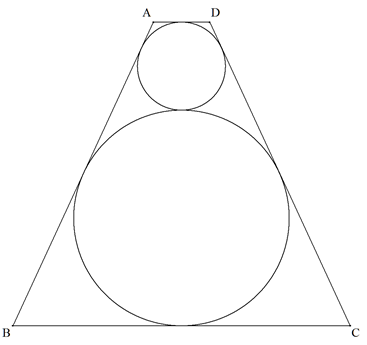

AD∥BC，AD＜BCである等脚台形ABCD内に，図のように2つの円は共有点をもたず，
それぞれ3辺に接している。AD=a，BC=bが一定であるとき，2つの円の直径の積の
値も一定になることを証明せよ。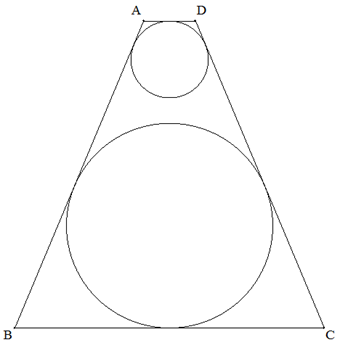