■趣味の数学問題集・Ａ問題

  1. 鋭角三角形ABCのBC上に点Dをとる。このDに対して，CA，AB上にそれぞれ点E，Fを，
    DE＋EF＋FDの値が最小になるようにとる。
    DE＋EF＋FDの値が最小になるとき，点Dの位置を定めよ。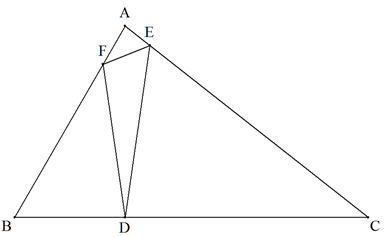



  2. 円x2+y2=r2上の定点A(-r,0)と動点Pについて，APの延長上に点QをPQ＝a（一定）と
    なるようにとる。点Pが点Aを除く位置のとき，QにおけるAQと垂直な直線は，
    ある曲線の接線になる。その曲線の方程式を求めよ。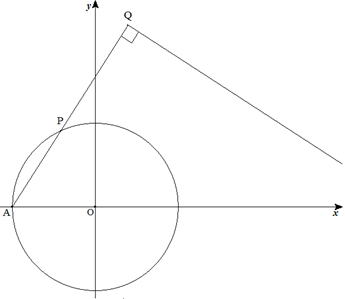



  3. 3次方程式 ax3＋bx2＋cx＋d＝0 の3つの解をα，β，γとするとき，
    次の3つの数を解にもつ3次方程式を1つ求めよ。
    (1)　α＋α-1，β＋β-1，γ＋γ-1
    (2)　α2＋αβ＋β2，β2＋βγ＋γ2，γ2＋γα＋α2


  4. 3次方程式 27x3＋27x2＋27x＋1＝0 の3つの解をα，β，γとするとき，
    α2＋αβ＋β2，β2＋βγ＋γ2，γ2＋γα＋α2の3つの数を解に
    もつ3次方程式を1つ求めよ。


  5. 3次方程式 x3＋664x＋2019＝0 について，
    (1)　実数解を求めよ。
    (2)　3つの解をα，β，γとおくとき，α2＋αβ＋β2の値を求めよ。


  6. 9√5，√582の小数部分はどちらが大きいか。


  7. 面積がS，∠C＝90°である△ABCに，図のようにn個の長方形が内接している。
    （図は5個の場合）
    n個の長方形の面積の和の最大値を求めよ。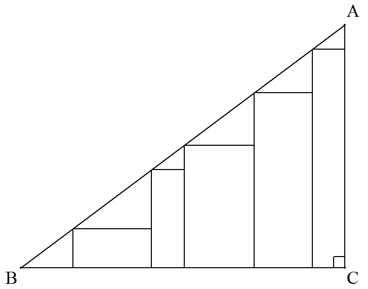



  8. 3辺AB，BC，CAが等差数列をなす△ABCについて，外心をO，内心をIとするとき，OI⊥AIを証明せよ。


  9. CA＝5，AB＝8である△ABCについて，5点B，外心O，内心I，垂心H，Cが同一円周上にあるとき，BCを求めよ。


  10. 鋭角三角形の外心，内心，垂心，∠A内の傍心をそれぞれO，I，H，I1とする。
    ∠BOC－∠BIC＋∠BHC＋∠BI1Cの値を求めよ。


  11. (1)　正三角形4個分の図形を合同な3つの図形に分割せよ。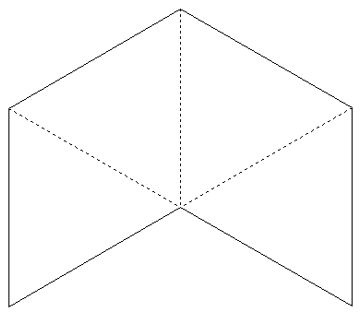
    (2)　正方形5個分の図形を合同な3つの図形に分割せよ。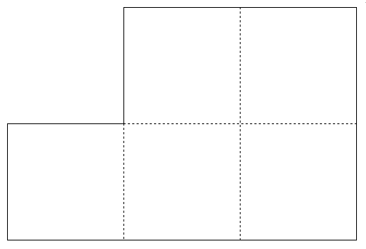
    (3)　正方形5個分の図形を合同な4つの図形に分割せよ。



  12. ひし形ABCDに図のように4個の半径rの円が内接している。
    ひし形の面積を求めよ。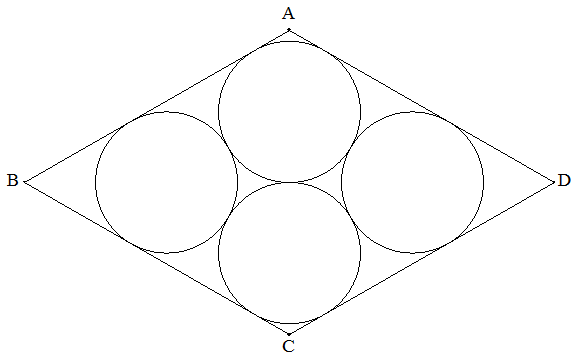



  13. AC＝14，BD＝48であるひし形ABCDに，図のように，
    4円P，Q，R，Sが内接している。
    ただし，円PとR，円QとSはそれぞれ半径が等しい。
    ひし形PQRSの内接円Oの半径を求めよ。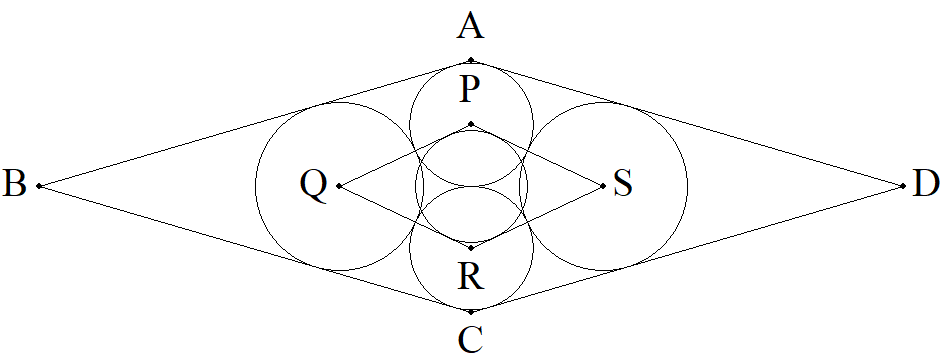



  14. 次の式は，2重根号を外せるか。



  15. 1辺の長さが9cmの正方形の折り紙がある。
    底辺の右側の頂点から2cmのところで図のように
    左側の頂点が対辺に重なるように折る。
    このとき，図に描かれている円の半径を求めよ。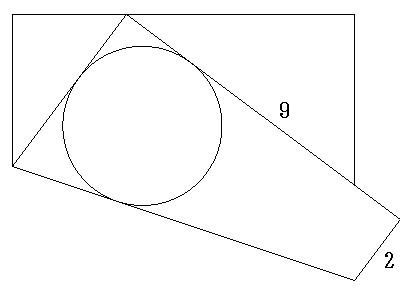



  16. 正方形の折り紙ABCDがある。
    図で，頂点Bが辺AD上のGに重なるように折るとき，
    折り目をEFとする。GD＝p，△DGIの内接円の半径を
    ｒとする。このとき，次の円の半径を求めよ。
    (1)　△AEGの内接円
    (2)　四角形GEFIの3辺IG，GE，EFに内接する円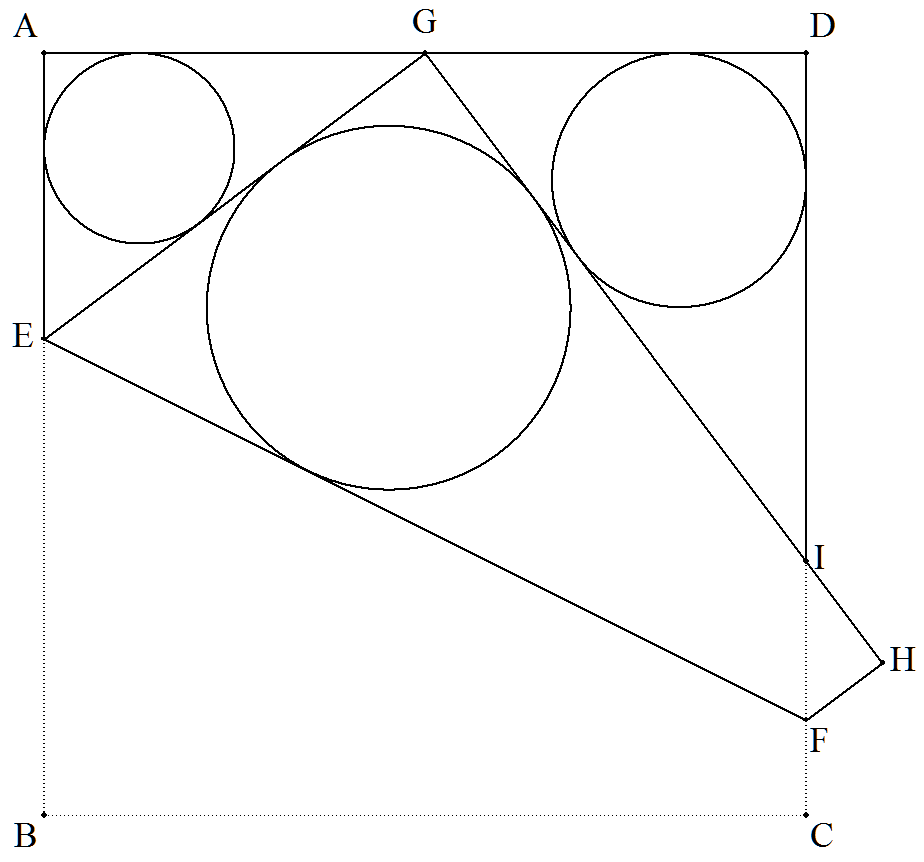



  17. 六角形ABCDEFについて，△ABF，△CDEは正三角形，
    四角形BCEFは正方形である。
    AD=aのとき，六角形の面積を求めよ。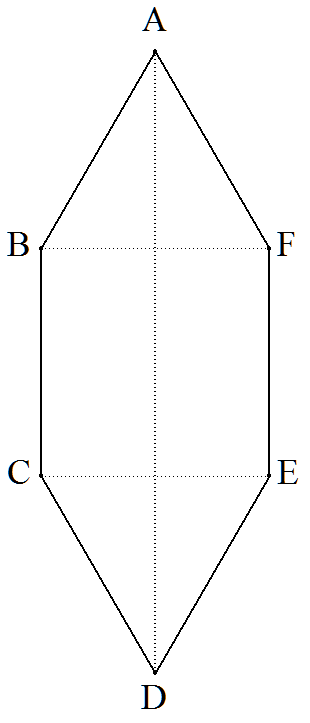



  18. 中心A(a，0)，半径r(r＞a＞0)の円Cに対して，
    第1象限で両軸と円Cに内接する円の半径をr1，
    第2象限で両軸と円Cに内接する円の半径をr2，
    第1象限で両軸と円Cに外接する円の半径をr3，
    第2象限で両軸と円Cに外接する円の半径をr4
    とする。このとき，次を証明せよ。
    (1)　r1－r2＋r3－r4＝4a
    (2)　r1r4＝r2r3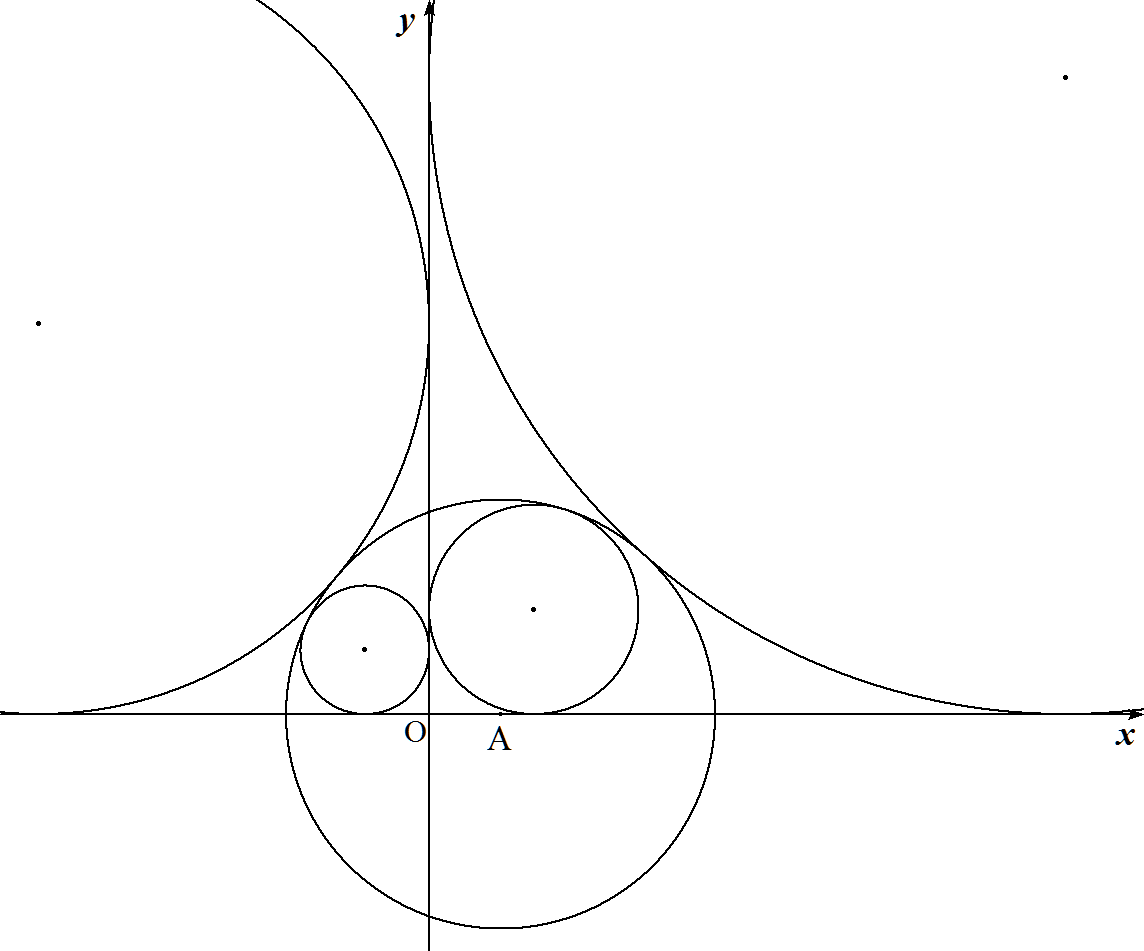



  19. 面積がSである四角形ABCDの対辺ADとBCの延長の交点をＥ，
    AC，BDの中点をそれぞれF，Gとすると，△EFG＝(1/4)Sと
    なることを証明せよ。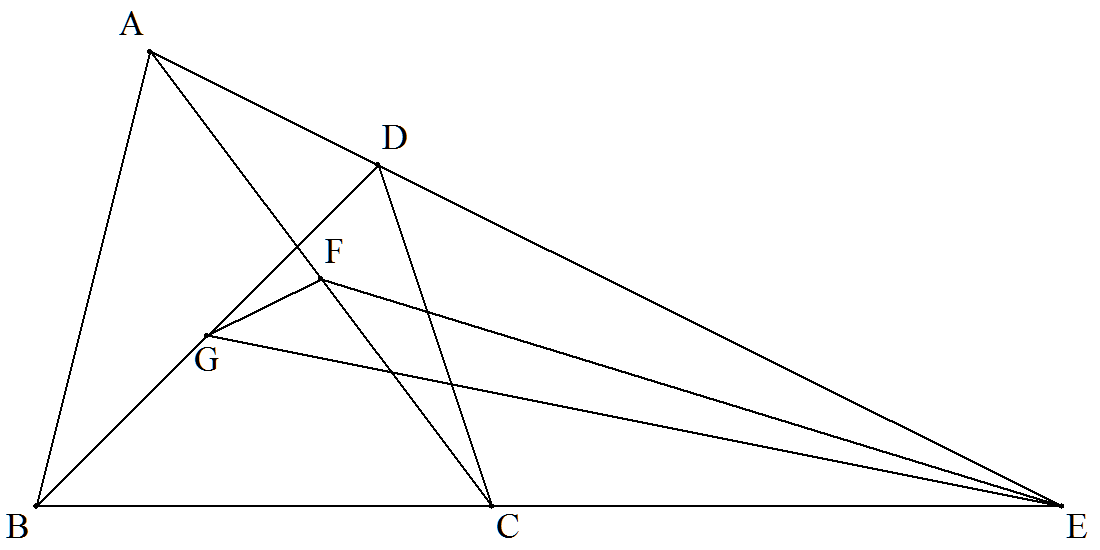



  20. 2円O1，O2の共通外接線の交角をα，
    共通内接線の交角をβとし，
    2円O1，O2の半径をそれぞれr1，r2とする。
    r2をr1を用いて表せ。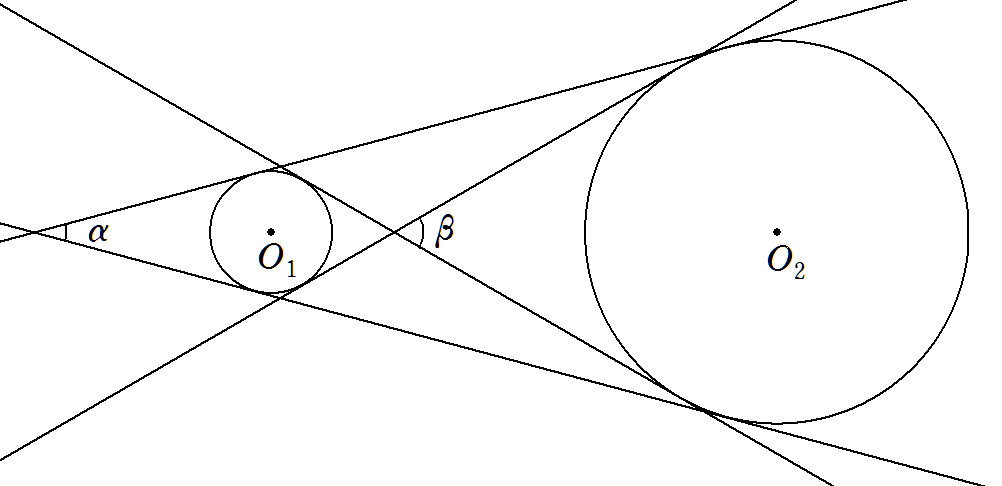



  21. BC>CA>ABである△ABCのBC， CA上に点D，Eを，線分DEが△ABCの内接円に接し，
    ∠EDC＝Aとなるようにとる。
    また，AD，BEの中点をそれぞれF，Gとする。
    このとき，△CFG/△ABCの値を求めよ。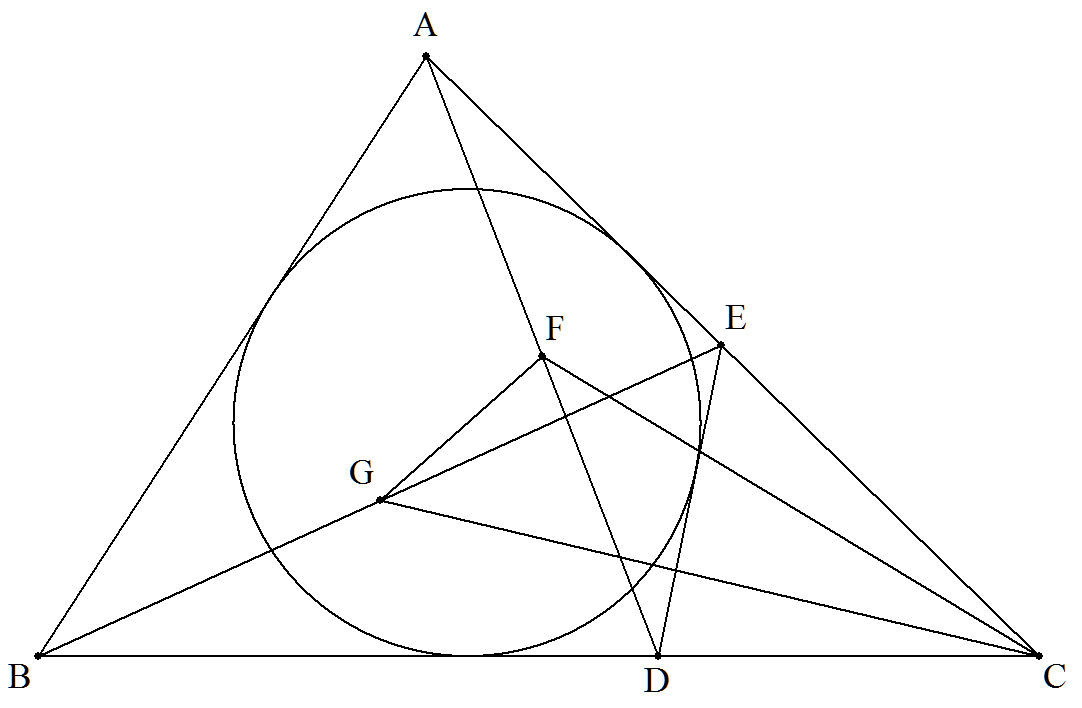



  22. △ABCのAB，ACを対角線とする
    正方形ADBE，AFCGをつくる。
    BCの中点をMとするとき，
    △MGD－△MEF＝△ABC
    を証明せよ。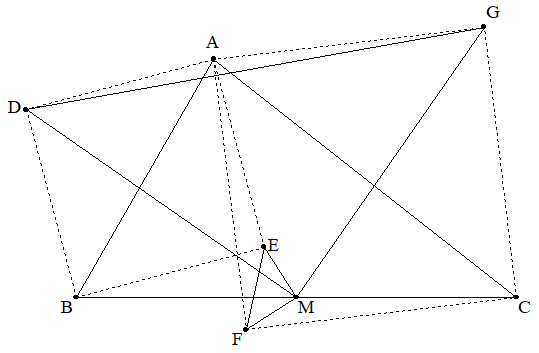



  23. 平面上の2点O1，O2について，O1O2＝d，点Qは
    円O1（r1）上を，点Rは円O2（r2）上を動くとき，
    線分QRをm：nに内分する点Pの軌跡の通過する
    領域の面積を求めよ。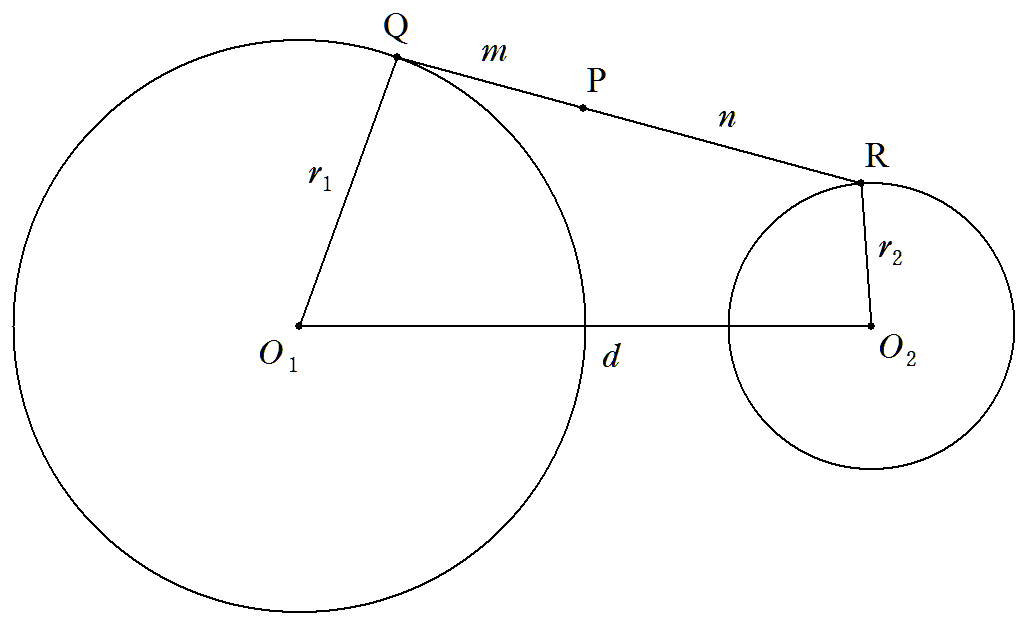



  24. ∠A＝90°である△ABCの内心をIとし，
    CIとABの交点をDとする。
    AD＝24，BI＝35のとき，BCを求めよ。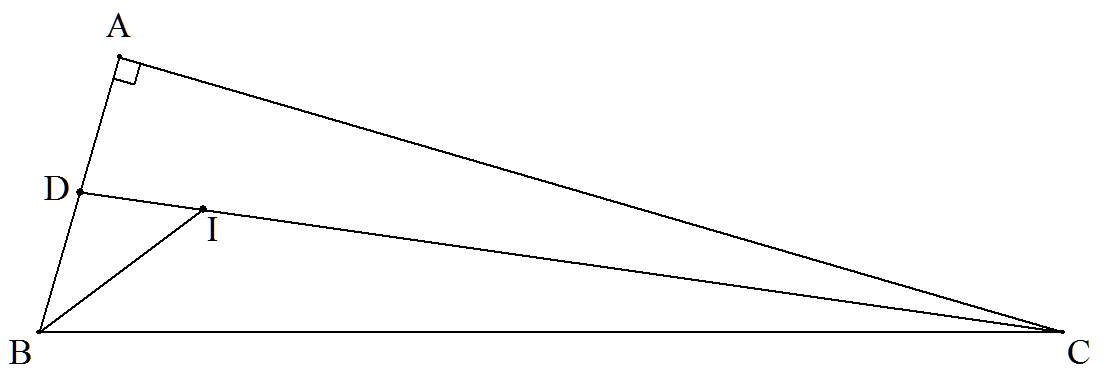



  25. a=6，b=5，c=4である△ABCの内心を
    Iとし，AIとBCの交点をDとする。
    △ABD，△ADCの内心をそれぞれJ，
    Kとするとき，△IJKの面積を求めよ。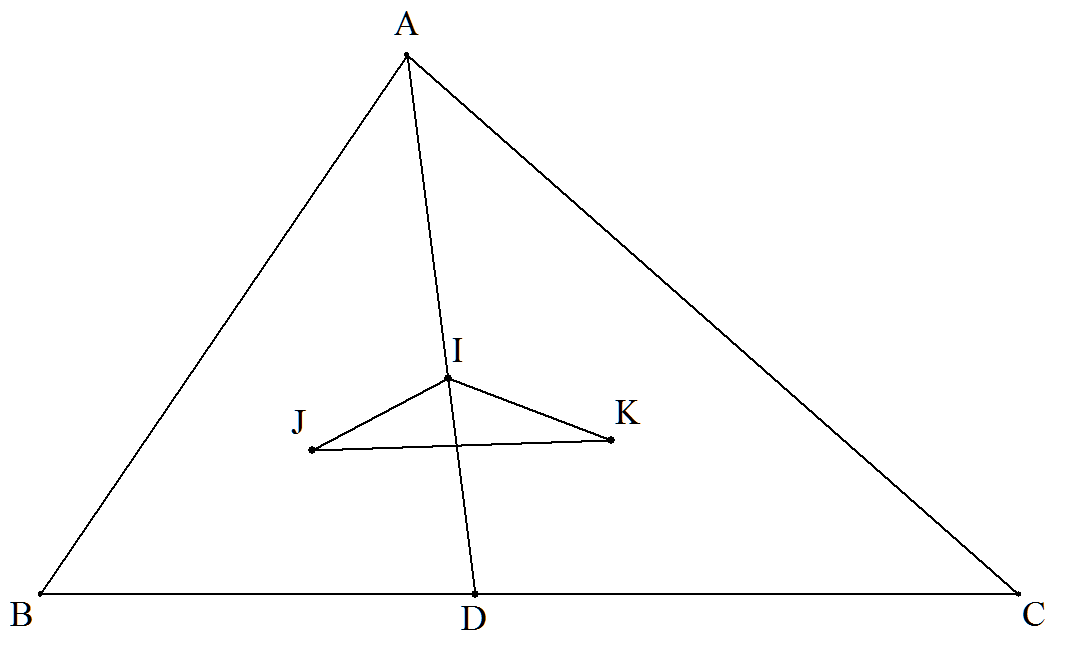



  26. a=6，b=5，c=4である△ABCの外心を
    Oとし，AOとBCの交点をDとする。
    △ABD，△ADCの外心をそれぞれP，
    Qとするとき，△OPQの面積を求めよ。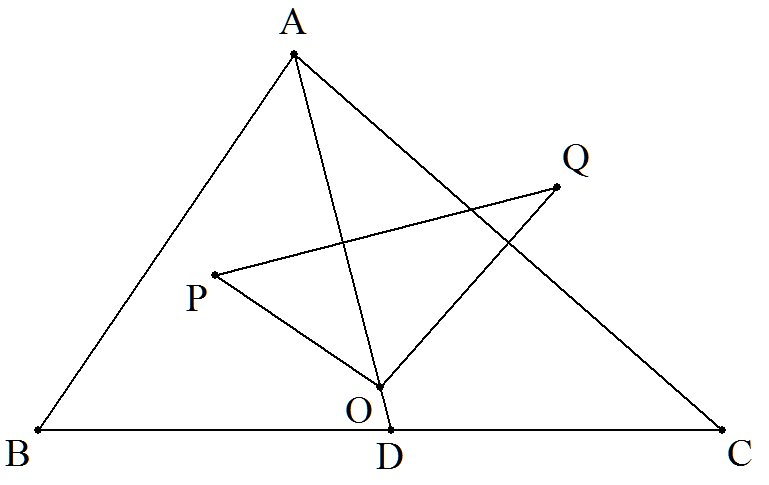



  27. a=6，b=5，c=4である△ABCの∠A内の傍心を
    Iとし，AIとBCの交点をDとする。
    △ABD，△ADCの∠A内の傍心をそれぞれJ，
    Kとするとき，△IJKの面積を求めよ。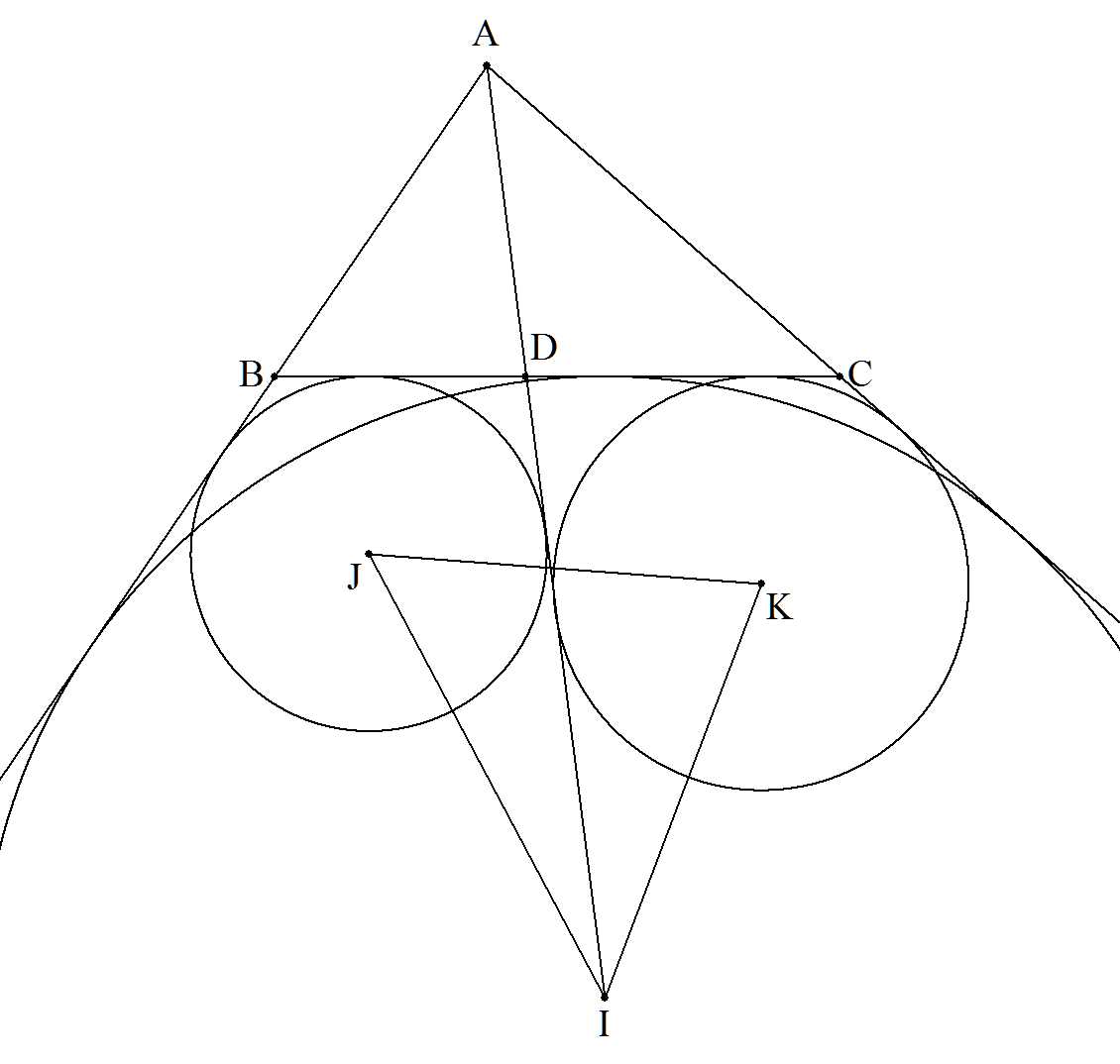



  28. △ABCの内心と∠A内の傍心をそれぞれI，Lと
    し，ALとBCの交点をDとする。
    △ABDの内心と∠A内の傍心をそれぞれJ，M，
    △ADCの内心と∠A内の傍心をそれぞれK，Nと
    するとき，△IJK/△LMNの値を求めよ。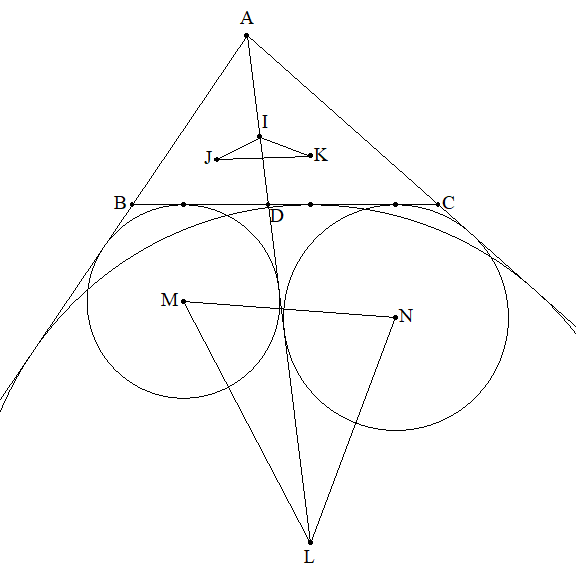



  29. △ABC内に点Pをとり，APとBC，BPとCA，CPとABとの交点
    をそれぞれD，E，Fとする。BP：PE＝e1：e2，CP：PF＝f1：f2，
    (e1f1-e2f2)/(e1+e2)(f1+f2)=kとおくとき，AP：PDを求めよ。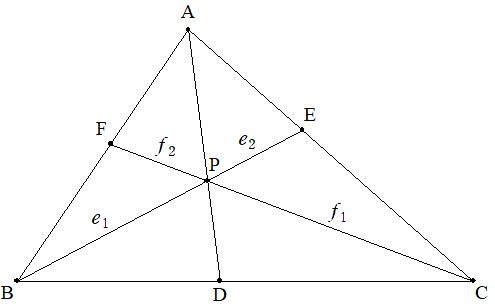



  30. △ABCの外側に各辺を底辺とする直角二等辺
    三角形PCB，QAC，RBAをつくる。
    四角形ARPQ－△ABCの値を求めよ。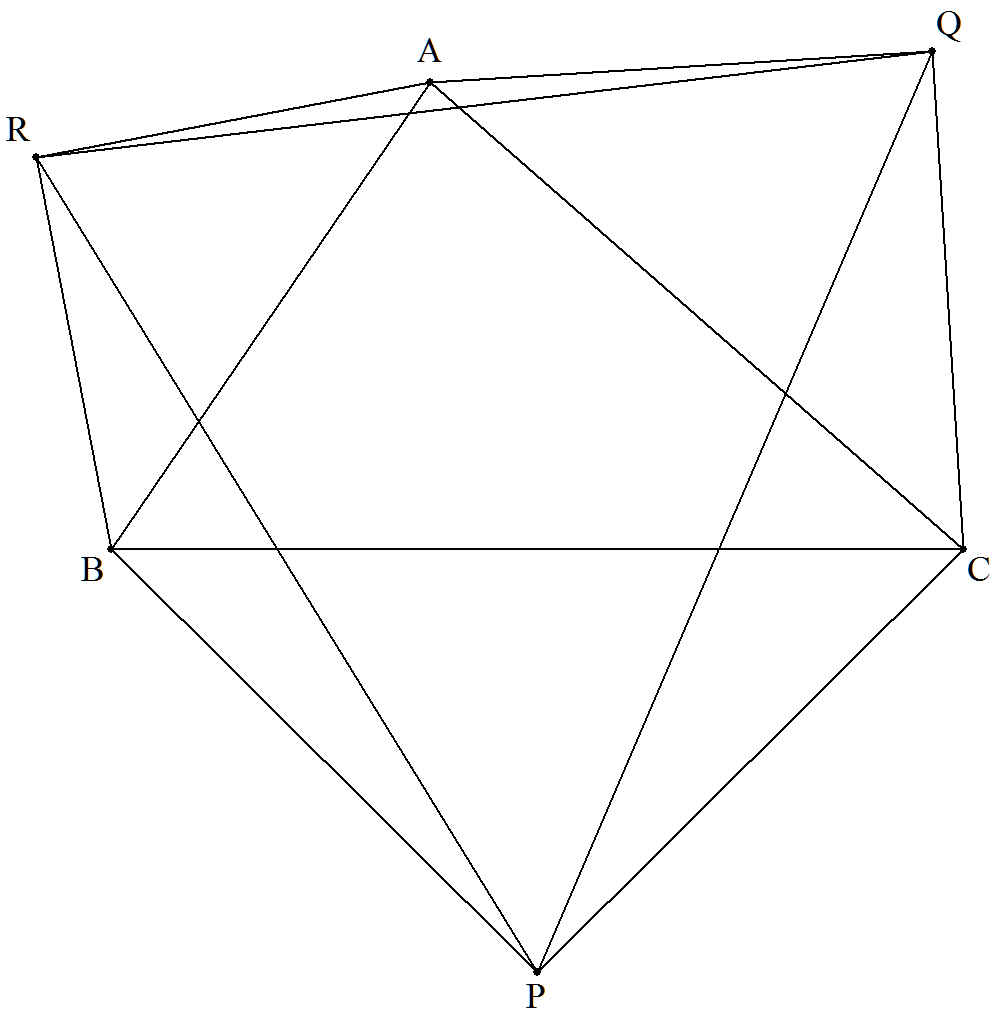



  31. △ABCの外側に各辺を底辺とする直角二等辺
    三角形PCB，QAC，RBAをつくる。
    BC，CA，ABの中点をそれぞれD，E，Fとし，DP，
    EQ，FRの中点をそれぞれL，M，Nとする。
    △PQR＝六角形ANBLCMとなることを証明せよ。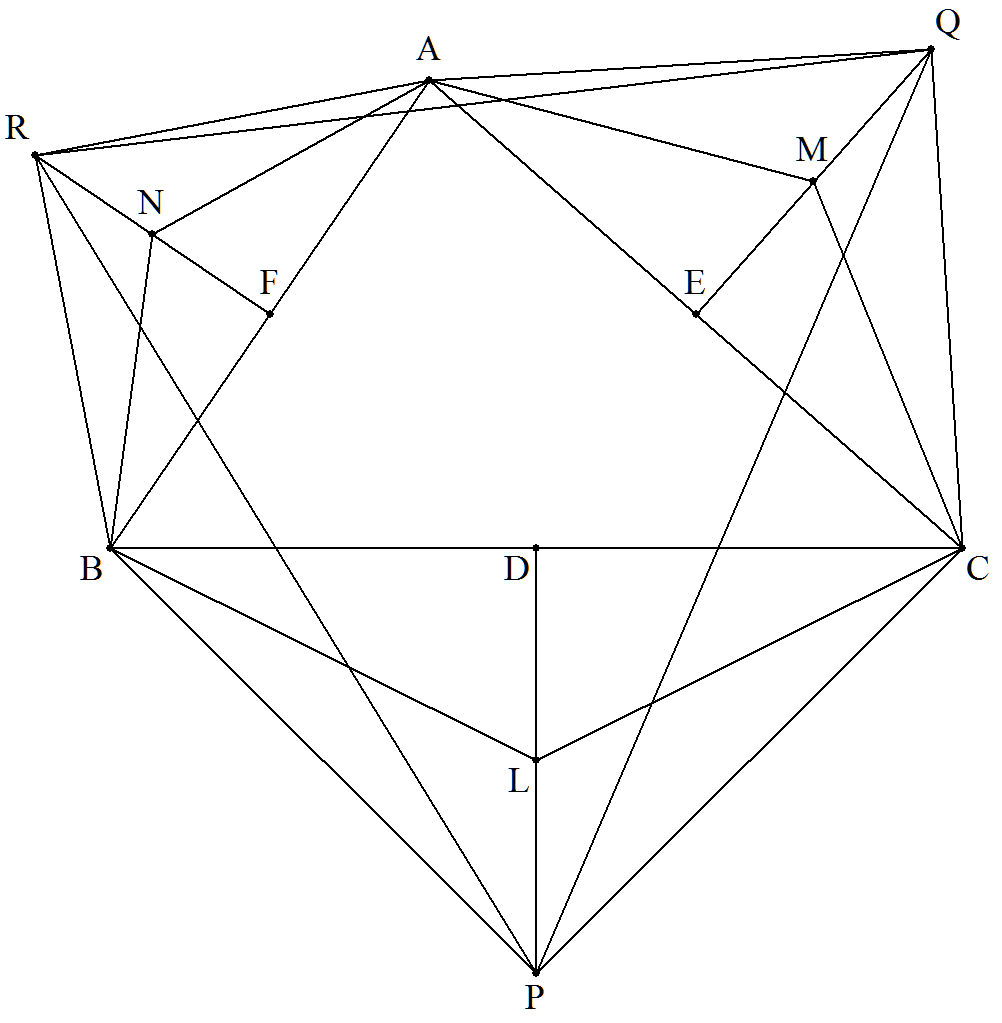



  32. △ABCについて，BCの延長上に点Dをとり，CA上
    に点Eをとる。CEを延長し，ABとの交点をFとする。
    AF＝6，FB＝18，BC=15，CE＝7，EF=10のとき，
    AE，ED，CDをそれぞれ求めよ。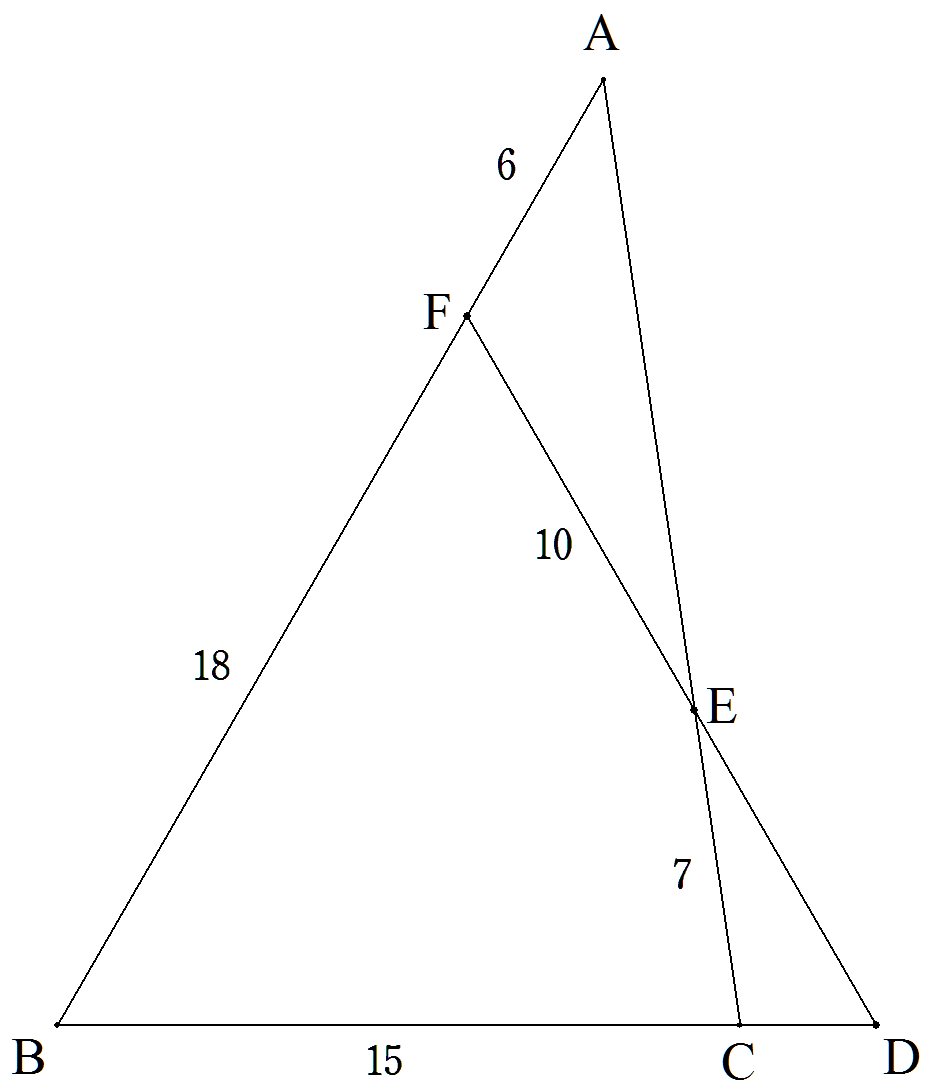



  33. 放物線y=px2+q（p≠0）上に異なる3点A，B，Cがあり，
    直線AB，BC，CAが原点を中心とする半径1の円に
    接するとき，p，qの条件を求めよ。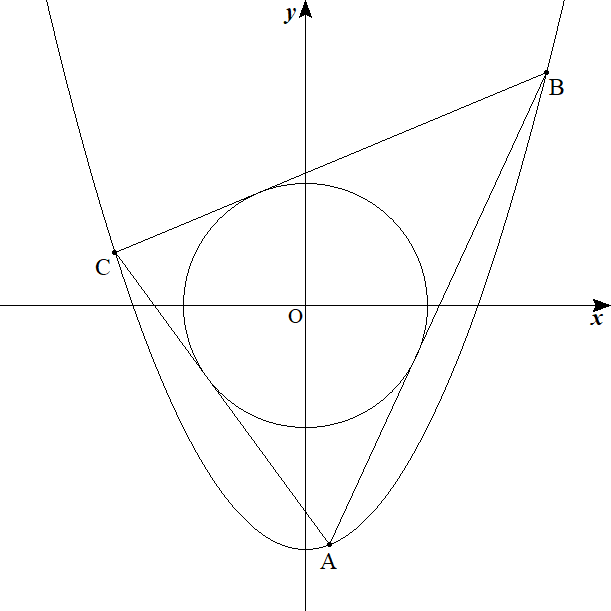



  34. 原点を中心とする円に外接する正方形
    DEFGについて，頂点Dは第2象限にあり，
    辺DEはy軸に平行である。
    y軸を軸とする放物線上の異なる3点を
    A，B，Cとし，直線AB，BC，CAがこの円
    に接するとき，放物線は正方形の2つの
    頂点を通ることを証明せよ。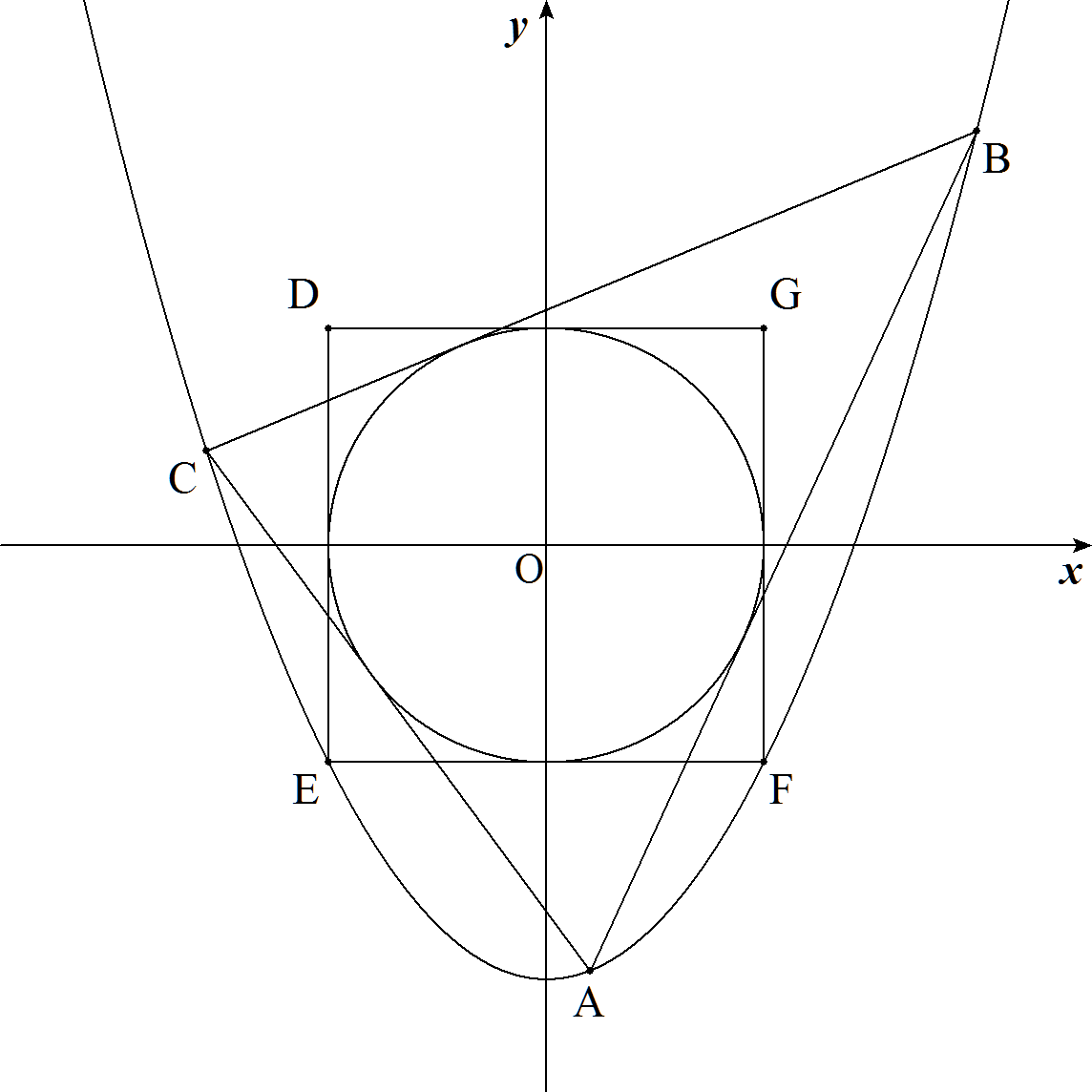






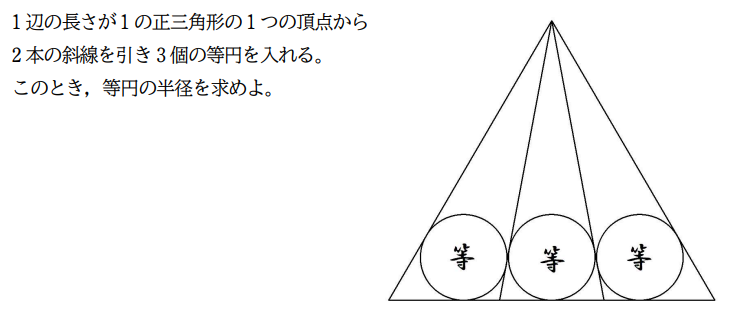
  36. 正方形ABCDの辺DAの中点をEとする。
    △EBC，△ECD，△EABの内心をそれぞれ
    P，Q，Rとする。EBとRQ，RPとの交点
    をそれぞれF，Gとする。
    このとき，4点F，G，P，Qは同一円周上に
    あることを証明せよ。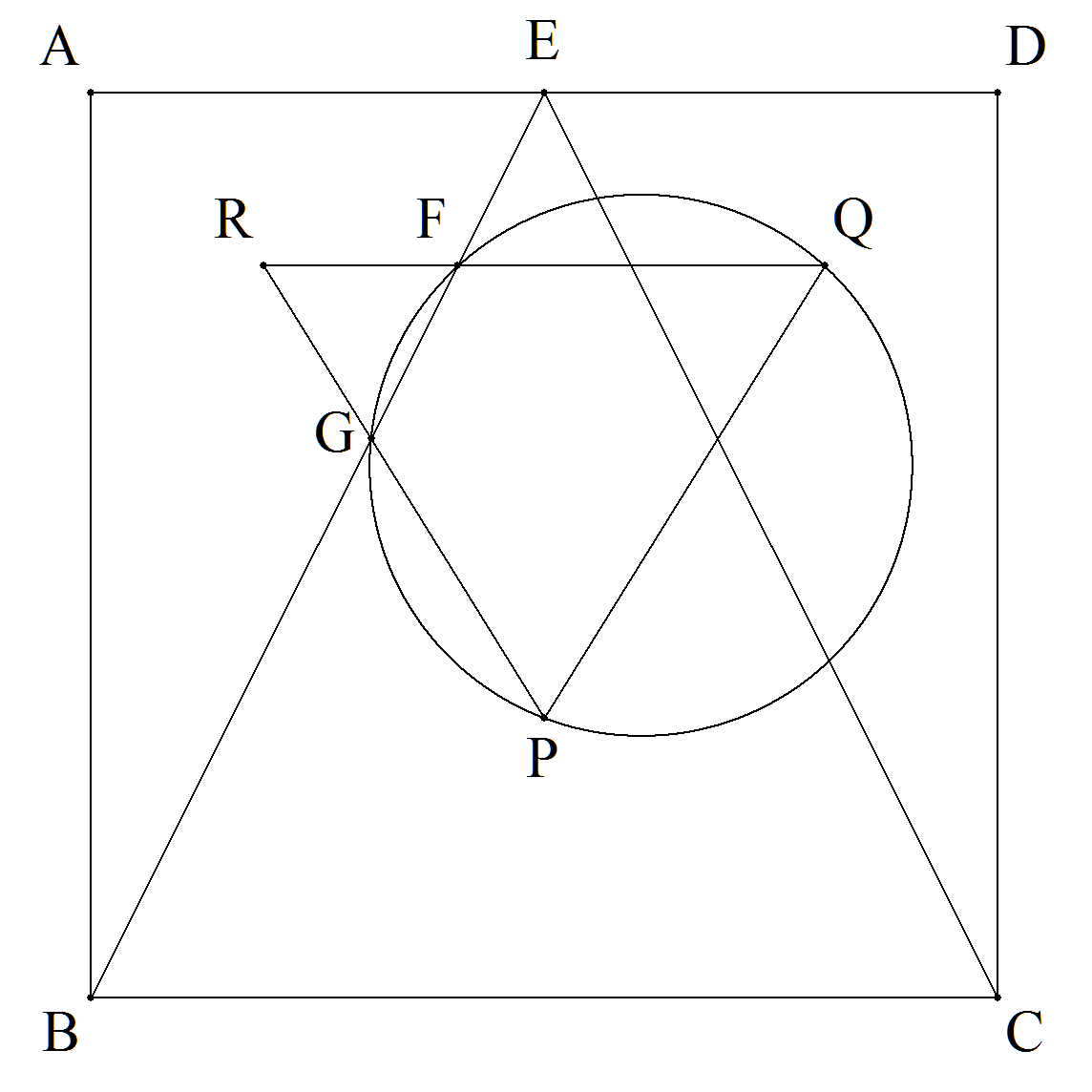



  37. 定円に外接する△ABCと正方形DEFGがある。
    このとき，3点A，B，Cと正方形の2つの頂点を
    通る放物線が存在することを証明せよ。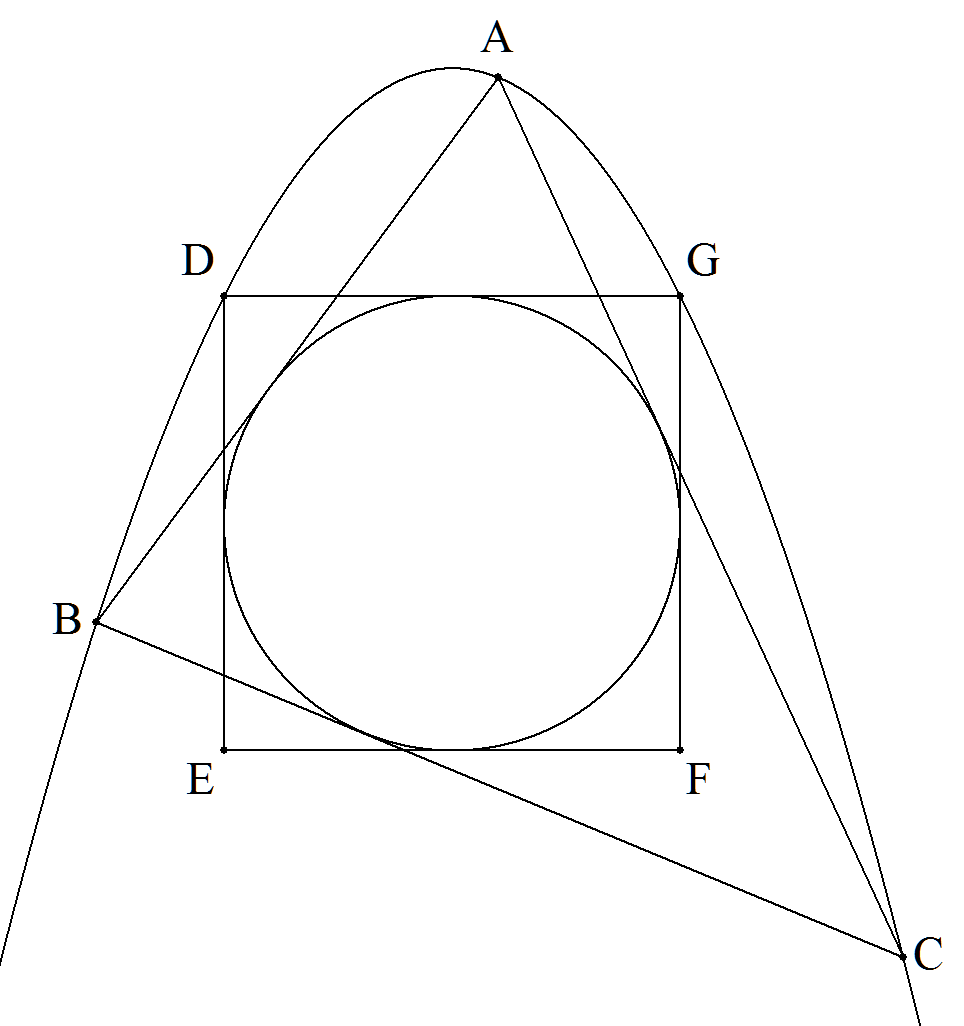



  38. △ABCにおいて，BC＝a，∠ABC＝18°，∠BCA＝108°
    である。
    AB上に点Dを∠BCD＝90°となるようにとる。
    このとき，図のように△DBCに内接する正方形CEFGの
    1辺を求めよ。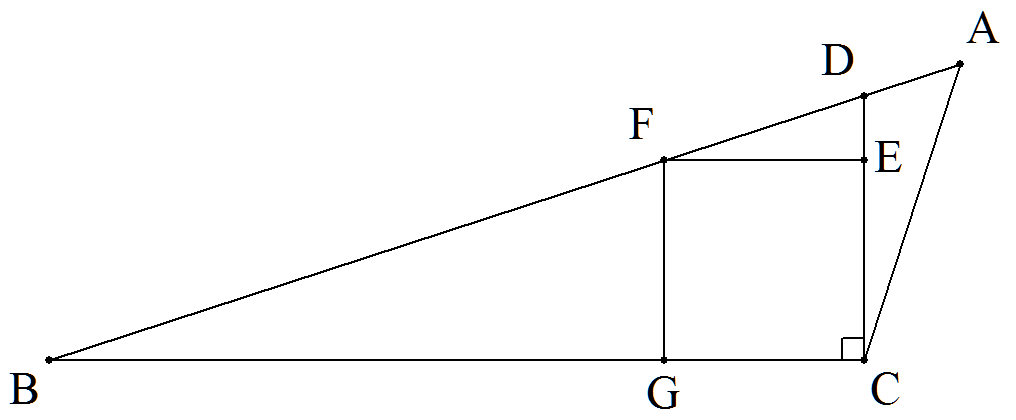



  39. 正三角形ABC内に点Pをとり，あらたに△LMNを，
    MN＝PA，NL＝PB，LM＝PCとなるようにつくる。
    ABを1辺とする正三角形の面積をS(AB)で表す。
    2S(AB)＝3△LMN＋S(PA)＋S(PB)＋S(PC)
    を証明せよ。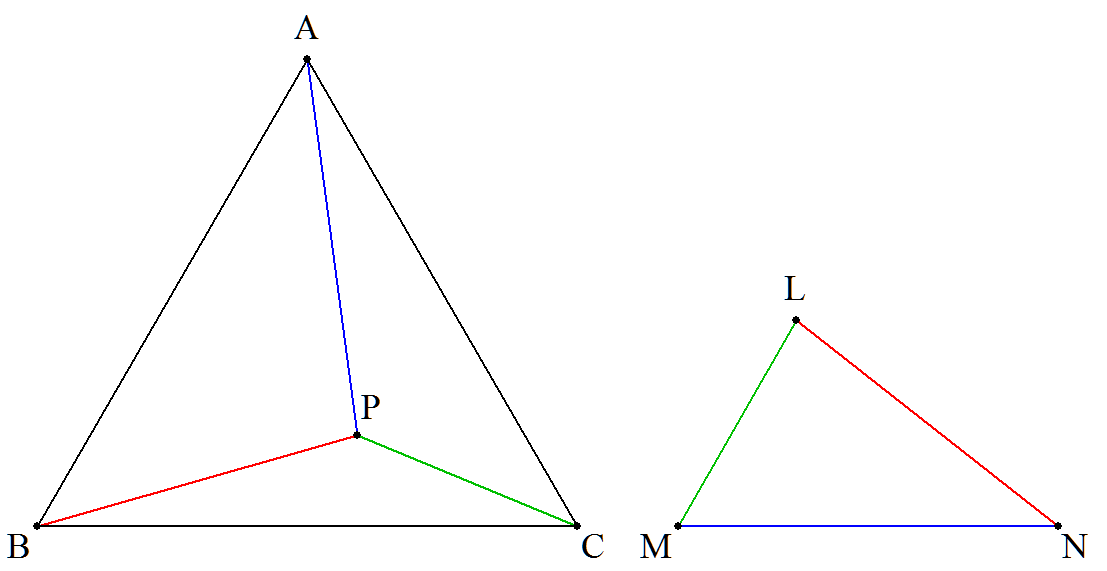



  40. 円Oとその弦BCが与えられている。この弦を底辺とし，
    この弦に対する優弧の上を動く点Aを頂点とする三角形を
    考える。この三角形の重心Gの軌跡を求めよ。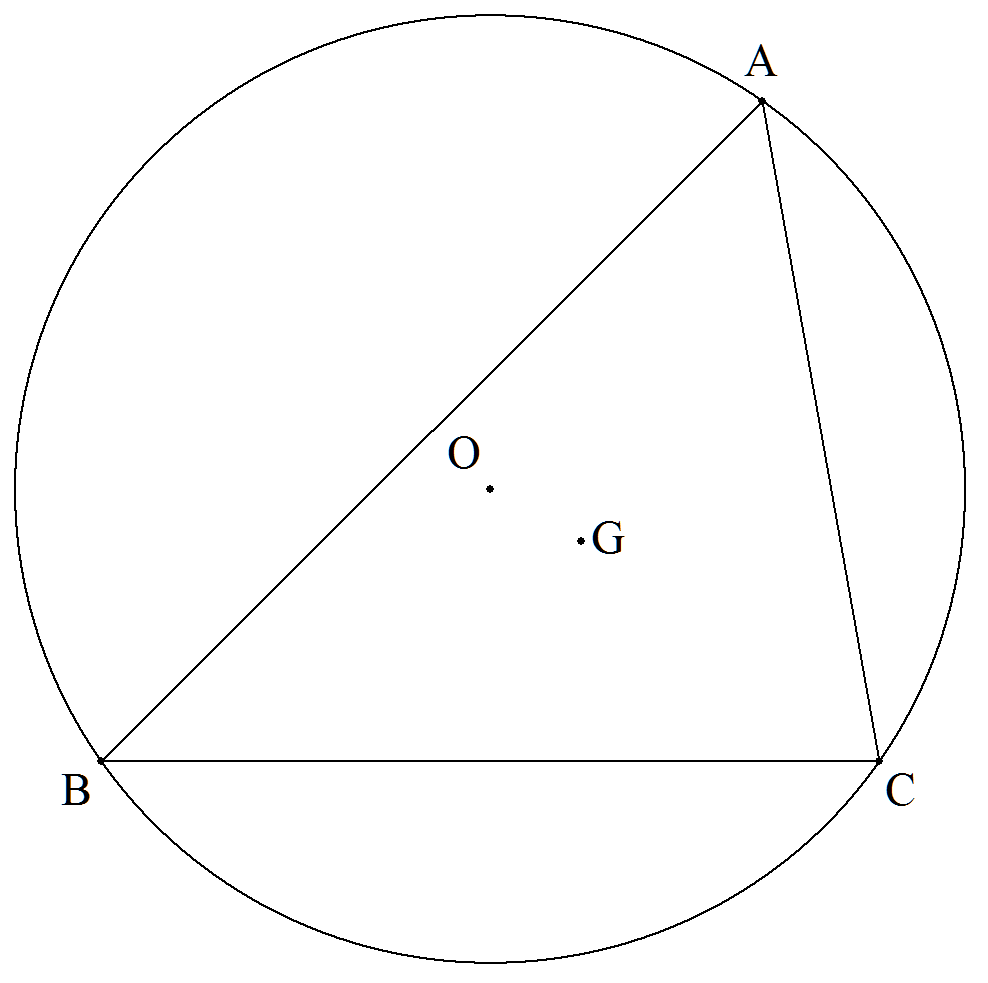



  41. 半径1の半円の中に図のように甲乙丙丁円が合計6個内接している。
    甲乙丙丁各円の半径を求めよ。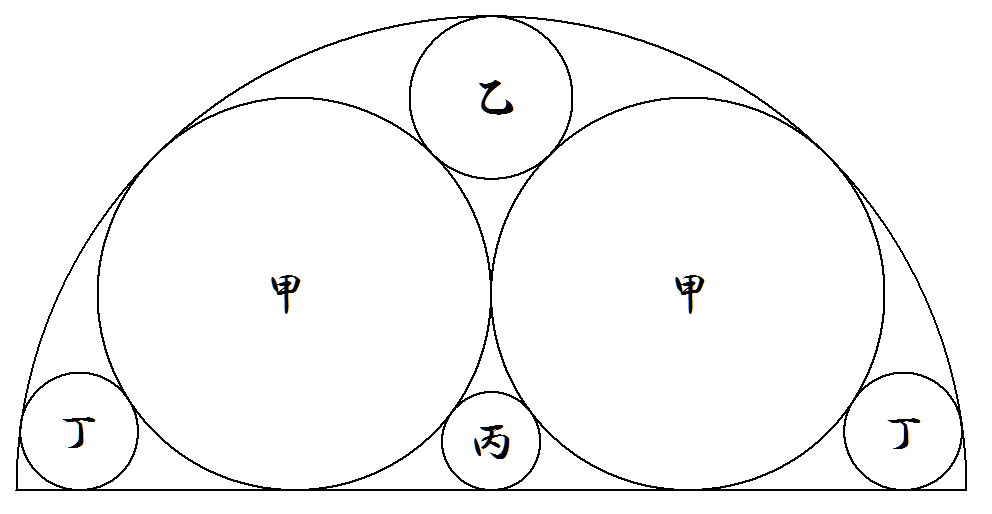



  42. 半径1の半円の中に図のように甲乙丙丁円が合計7個内接している。
    甲乙丙丁各円の半径を求めよ。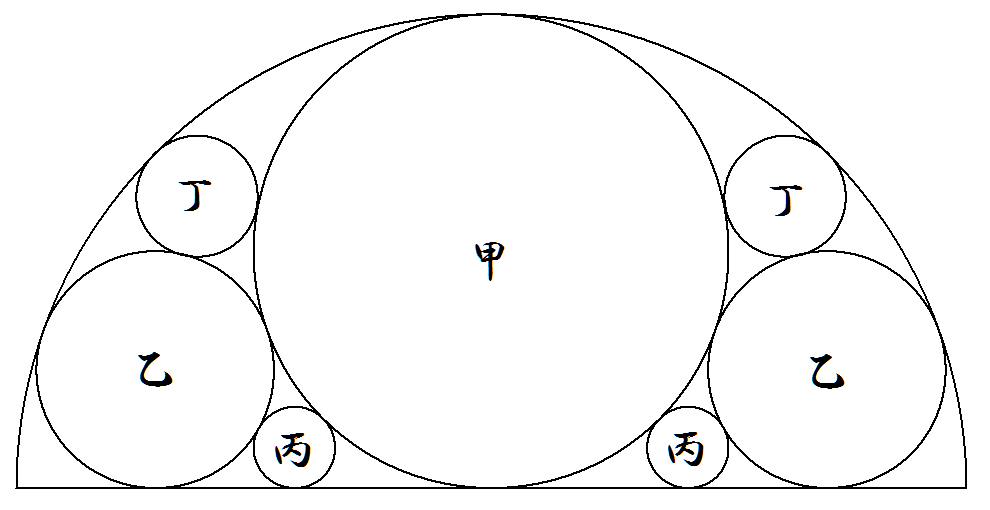



  43. 半径1の半円の中に図のように甲乙丙円が合計6個内接している。
    甲乙丙各円の半径を求めよ。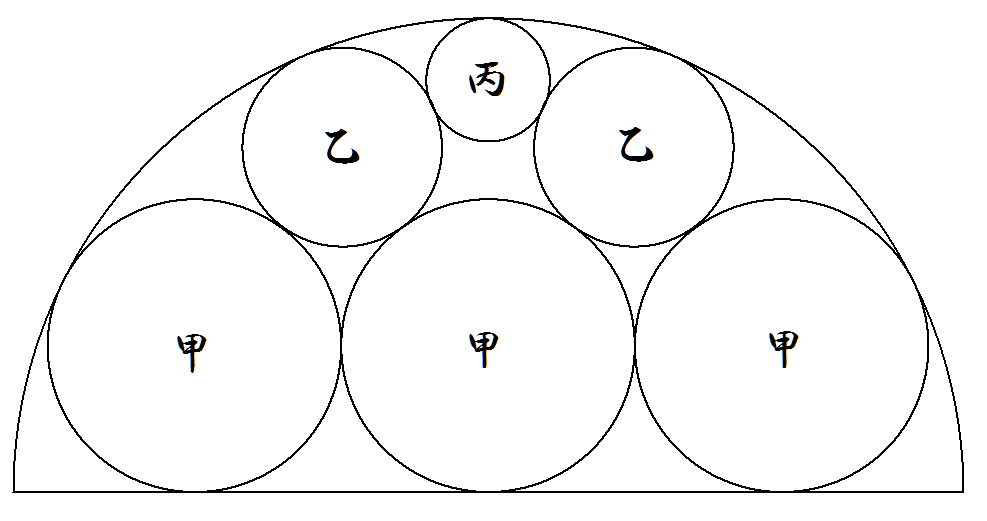



  44. MAKE2021
    1～9までの数字をこの順に一桁の数として使って，答が2021になる式を作れ。
    ただし，使用できる記号は，四則（＋，－，×，÷）と括弧のみとする。


  45. 扇形甲は，半径1の4分の1円で，乙円は，扇形甲に内接している。
    2つの丙半円は，図のように扇形甲の半径を直径とし，甲の内部にある。
    丁円は，2つの丙半円に外接し，乙円に内接している。
    戊円は，扇形甲の半径に接し，丙半円に内接し，もう一方の丙半円に
    外接している。 己円は，2つの丙半円と乙円に内接している。
    庚円は，丙半円に内接し，もう一方の丙半円に外接し，乙円に内接して
    いる。
    辛円は，扇形甲の半径に接し，丙半円に内接し，乙円に外接している。
    仁円は，2つの丙半円に内接し，乙円に外接している。
    癸円は，扇形甲に内接し，丙半円に外接し，乙円に外接している。
    (1)　丁円の半径を求めよ。
    (2)　戊円の半径を求めよ。
    (3)　己円の半径を求めよ。
    (4)　庚円の半径を求めよ。
    (5)　辛円の半径を求めよ。











    (6)　仁円の半径を求めよ。
    (7)　癸円の半径を求めよ。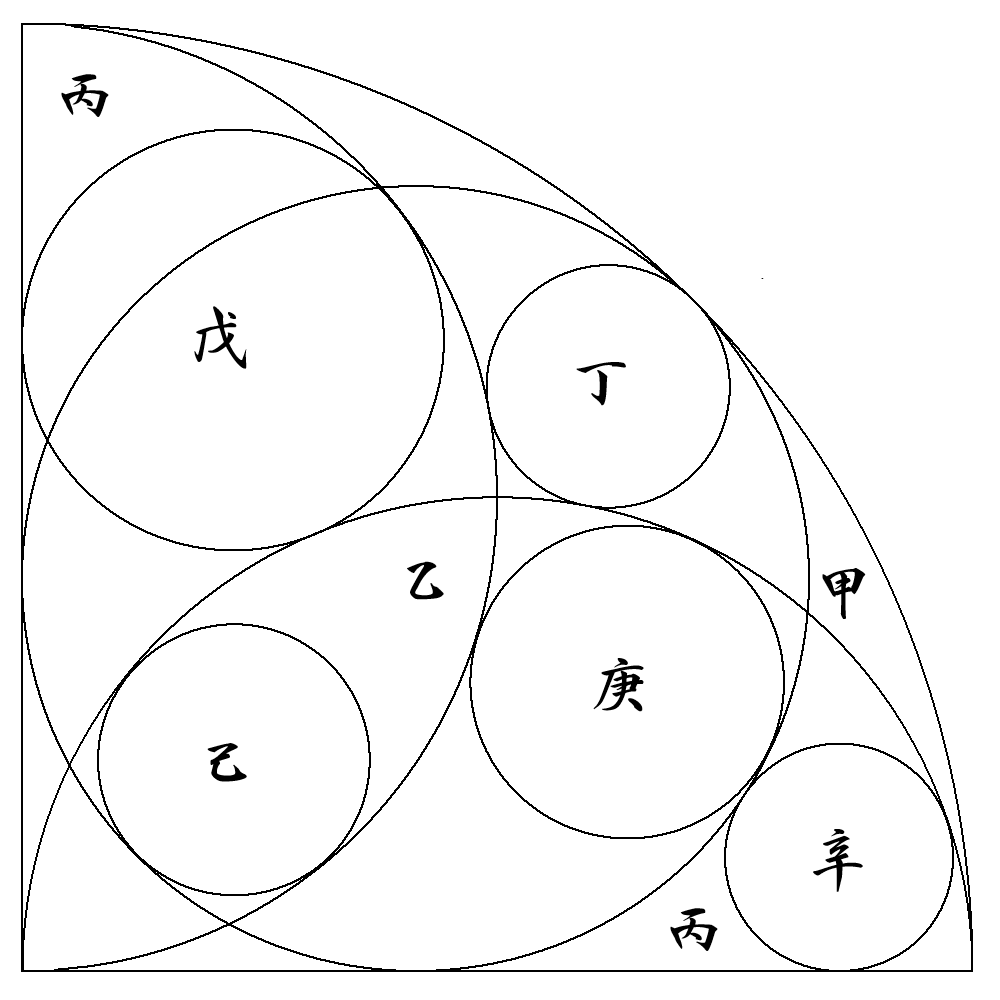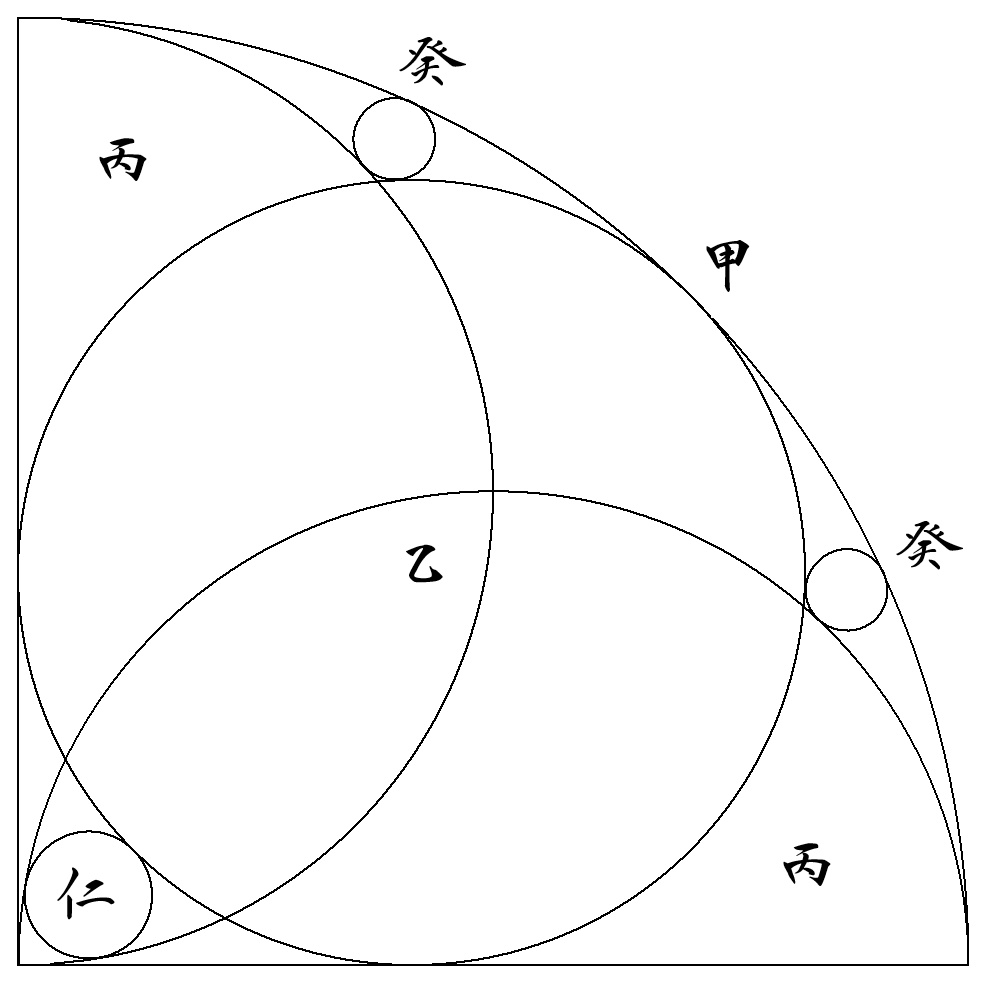



  46. 半径1の半円の中に図のように甲乙丙円が合計7個配置されている。
    甲乙丙各円の半径を求めよ。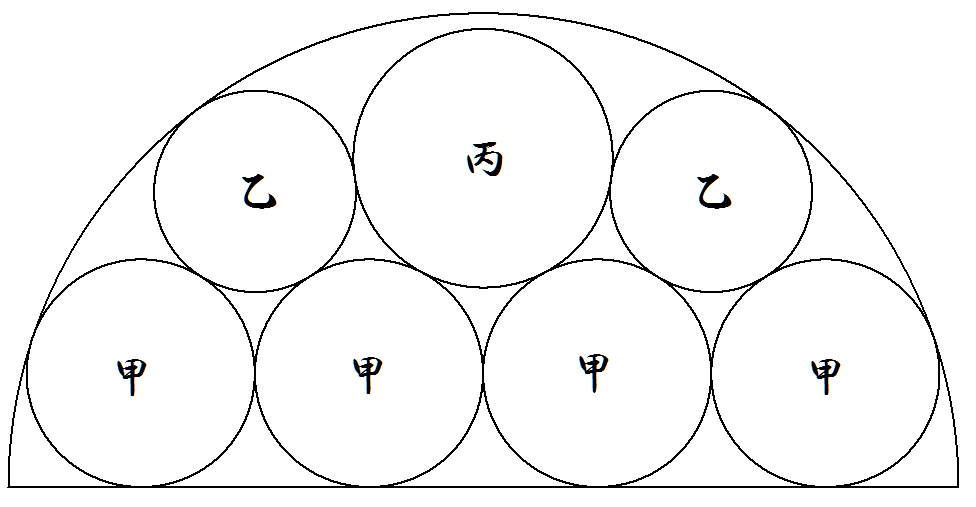



  47. 半径1の半円の中に図のように甲乙丙円が合計7個内接している。
    甲乙丙各円の半径を求めよ。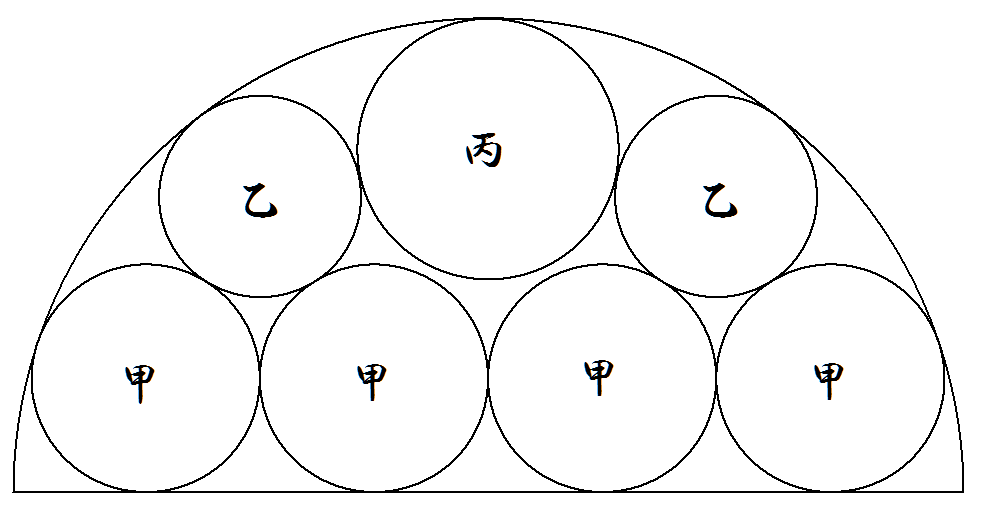



  48. 半径1の半円の中に図のように甲乙丙円が合計9個配置されている。
    甲乙丙各円の半径を求めよ。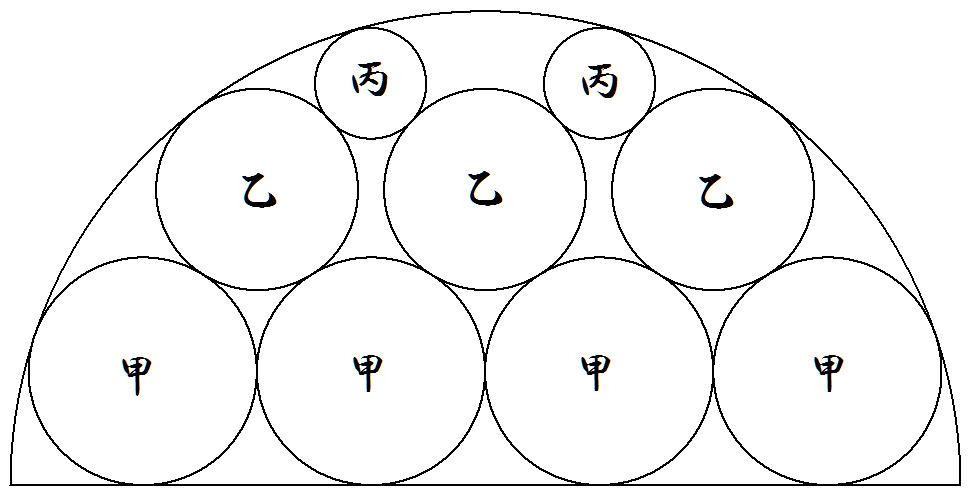



  49. 半径1の半円の中に図のように甲乙円が合計5個内接している。
    甲乙各円の半径を求めよ。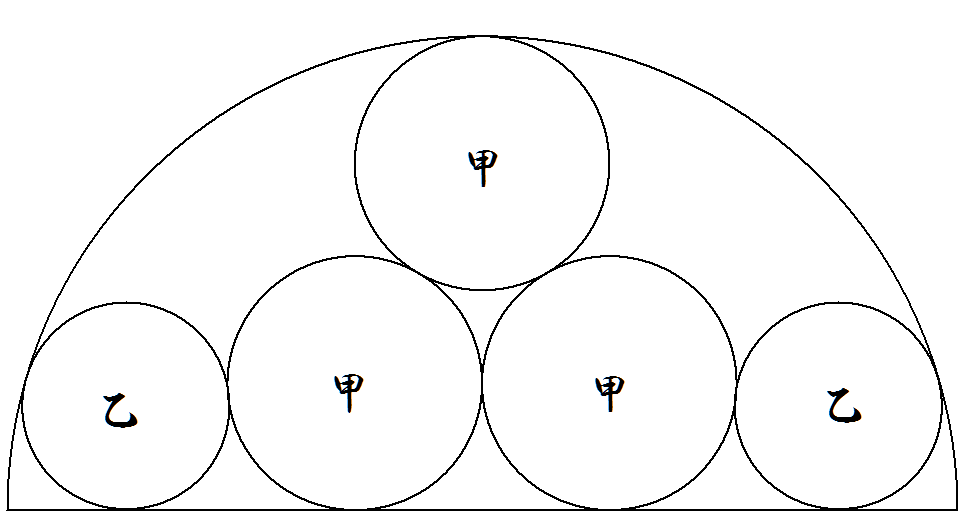



  50. 半径1の半円の中に図のように甲乙円が合計5個内接している。
    甲乙各円の半径を求めよ。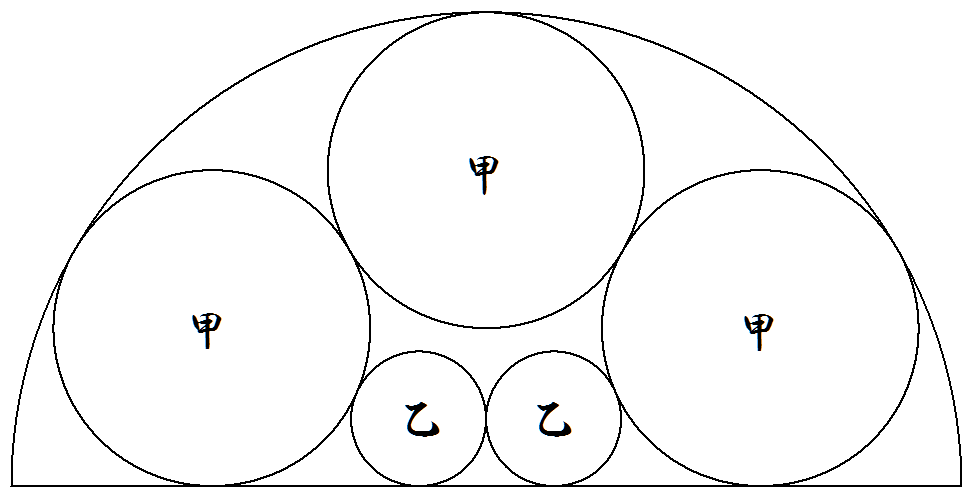