■趣味の数学問題集・Ａ問題

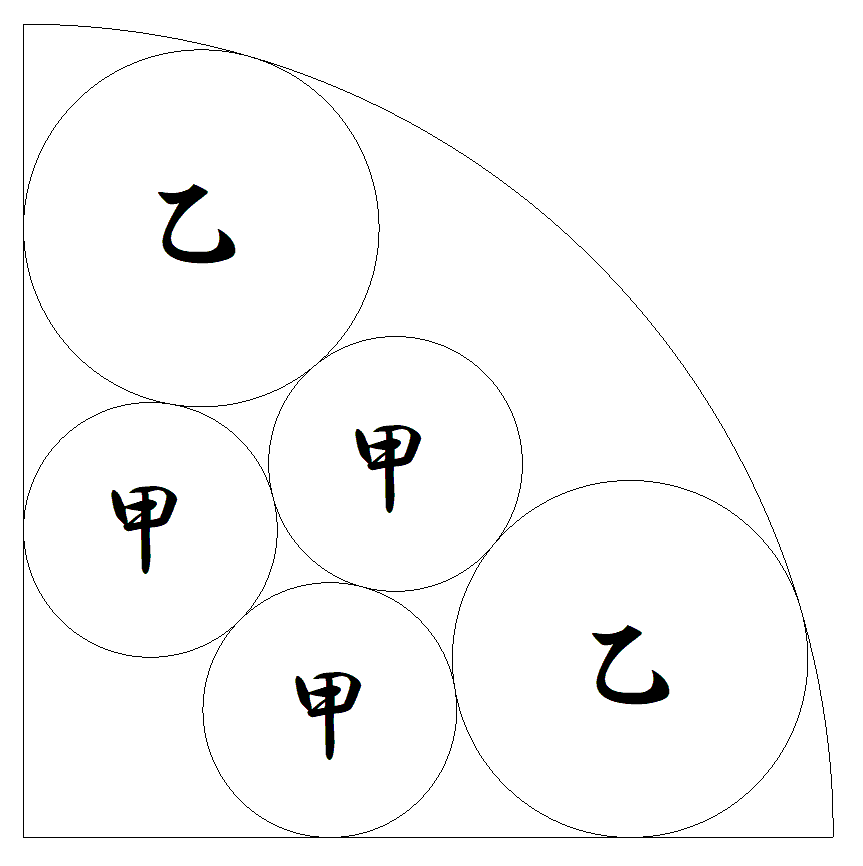
  1. 半径1の4分の1円内に図のように甲乙丙円4個が内接している。
    (1)　甲円の半径を求めよ。
    (2)　乙円の半径を求めよ。
    (3)　丙円の半径を求めよ。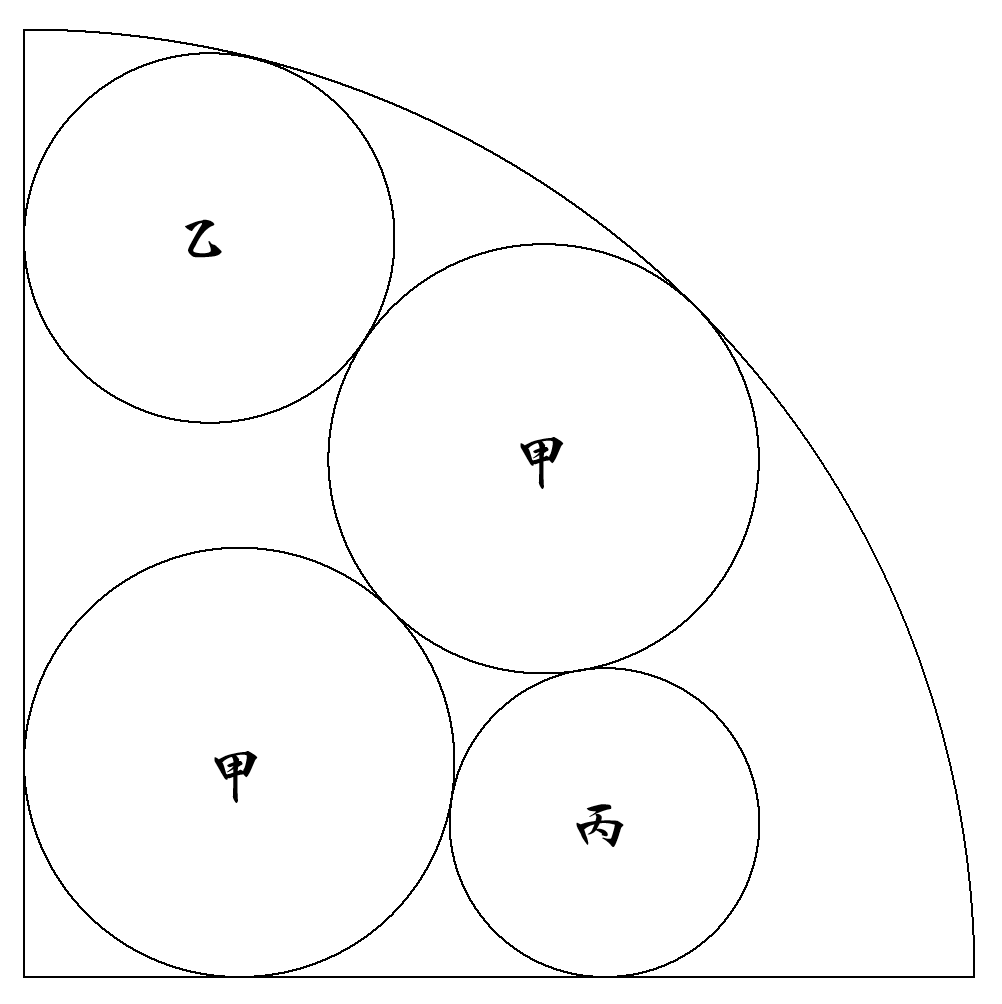



  2. 半径1の4分の1円内に図のように甲乙円4個が内接している。
    (1)　甲円の半径を求めよ。
    (2)　乙円の半径を求めよ。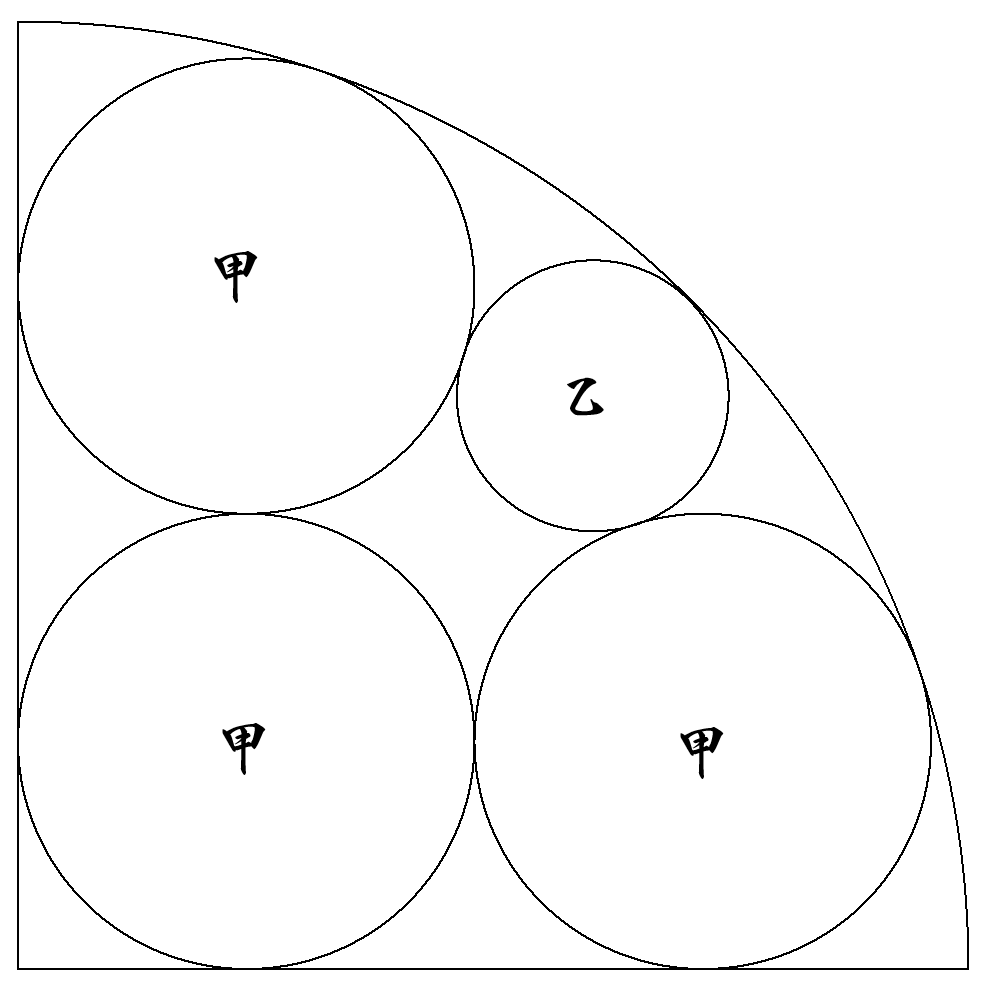



  3. 半径1の半円内に甲乙丙の8円が図のように内接している。
    各円の半径をそれぞれ求めよ。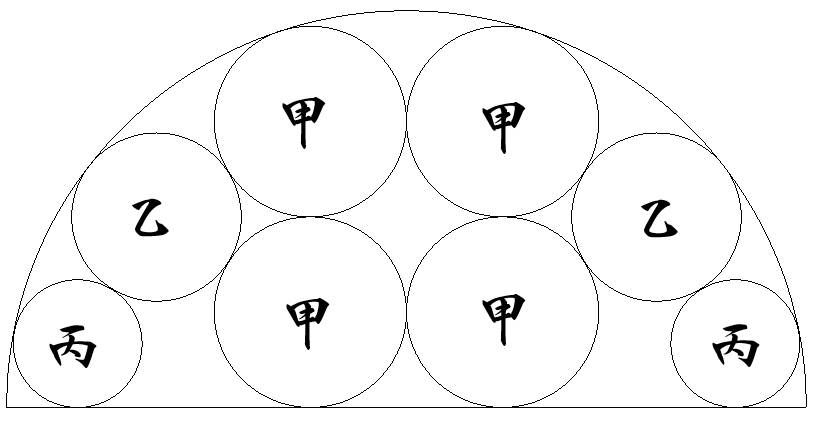



  4. (1)　半径1の半円内に9個の甲円が図のように配置されている。
    　甲円の半径を求めよ。
    (2)　1段目に2個，2段目に3個，3段目に4個，…，n段目に(n+1)個の
    　半径1の甲円が，図のように俵積みされている。
    　図は，n=3の場合。
    　それらを内側に含む半円の半径を求めよ。
    　ただし，1段目の2個の甲円は半円に内接し，n段目の
    　(n+1)個の甲円は半円の直径に接している。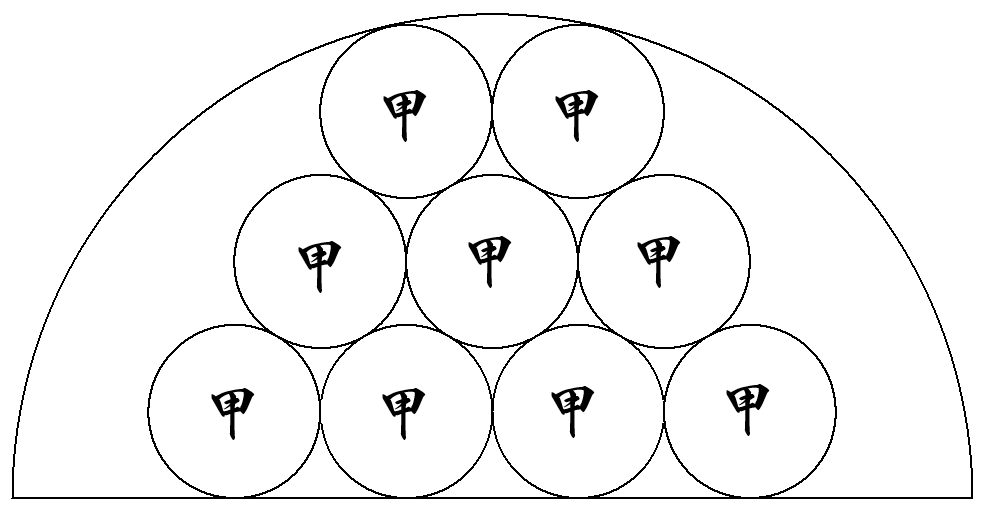



  5. 半径1の半円内に甲円5個が，図のように1つの甲円の周りの
    4つの甲円の中心が正方形の頂点をなすように配置されている。
    甲円の半径を求めよ。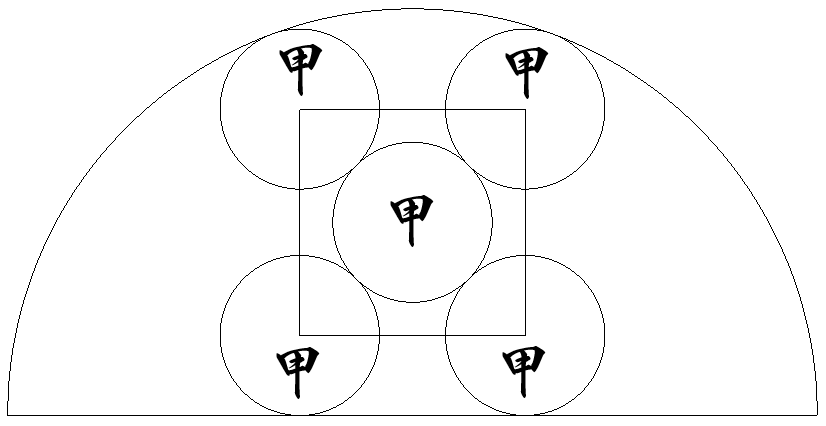



  6. 半径1の4分の1円内に，図のように甲円4個が，それぞれの円の中心が
    正方形の頂点になるように配置されている。
    甲円の半径を求めよ。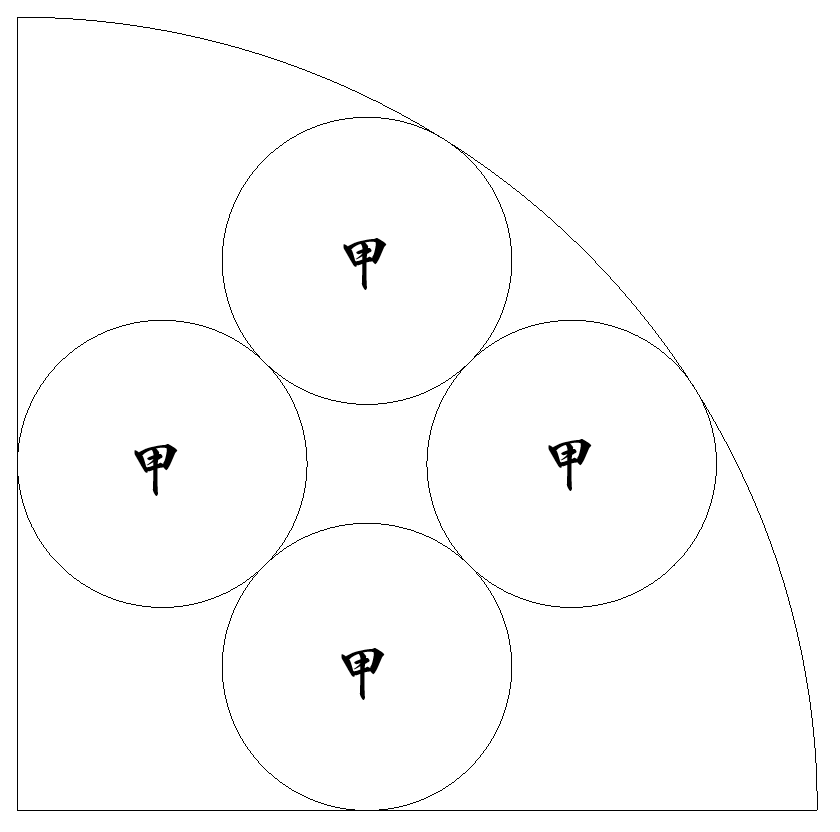



  7. 半径1の4分の1円内に，図のように甲円5個が，1つの甲円の周りの4つの
    甲円の中心が正方形の頂点をなすように配置されている。
    甲円の半径を求めよ。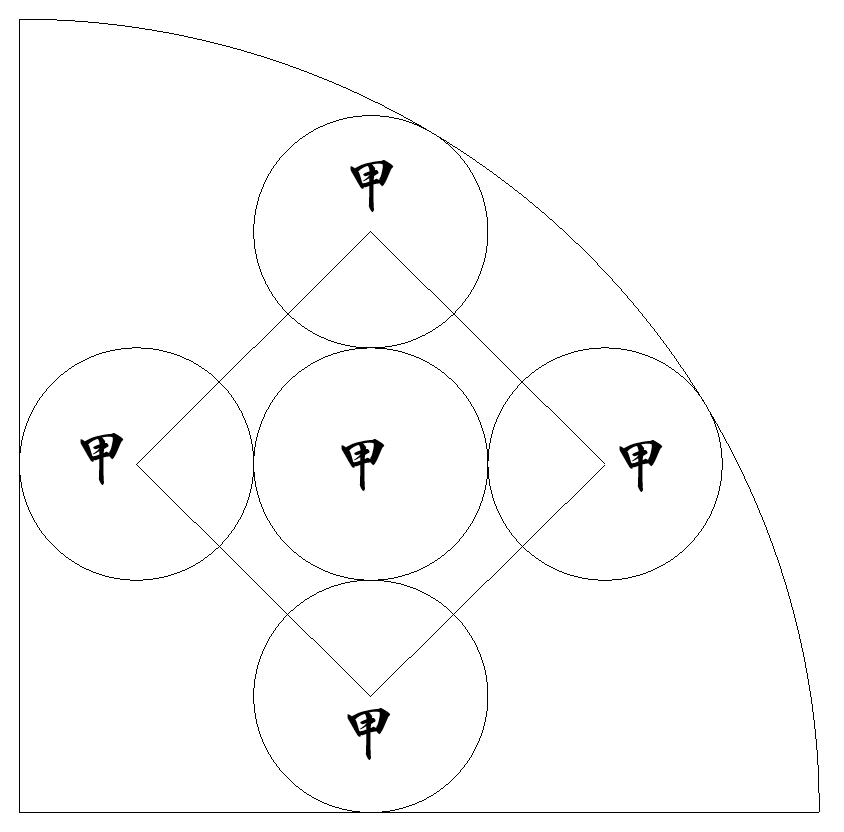



  8. 元号が平成から令和に変わった。
    (1)　西暦□□□□年（令和□□年）□月□□日の9個の□にはすべて異なる数字が入る。
    　最初に訪れる年月日を求めよ。
    (2)　曜日を次のように数字で表す。
    　月→1，火→2，水→3，木→4，金→5，土→6，日→7
    　西暦□□□□年（令和□□年）□月□□日（□曜日）の10個の□にはすべて異なる数字が入る。
    　令和70年までの中に，このような年月日（曜日）は9個あることが知られている。
    　最初に訪れる年月日（曜日）を求めよ。


  9. 半径1の4分の1円内に，図のように甲乙丙円4個が内接している。
    各円の半径をそれぞれ求めよ。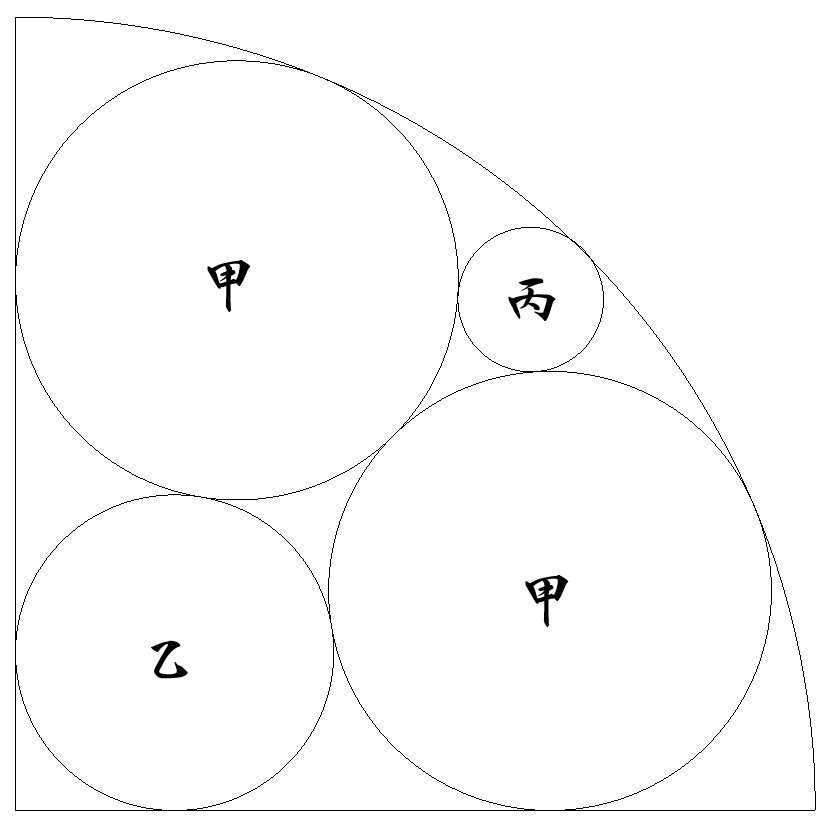



  10. 半径1の4分の1円内に，図のように甲乙丙丁円6個が内接している。
    各円の半径をそれぞれ求めよ。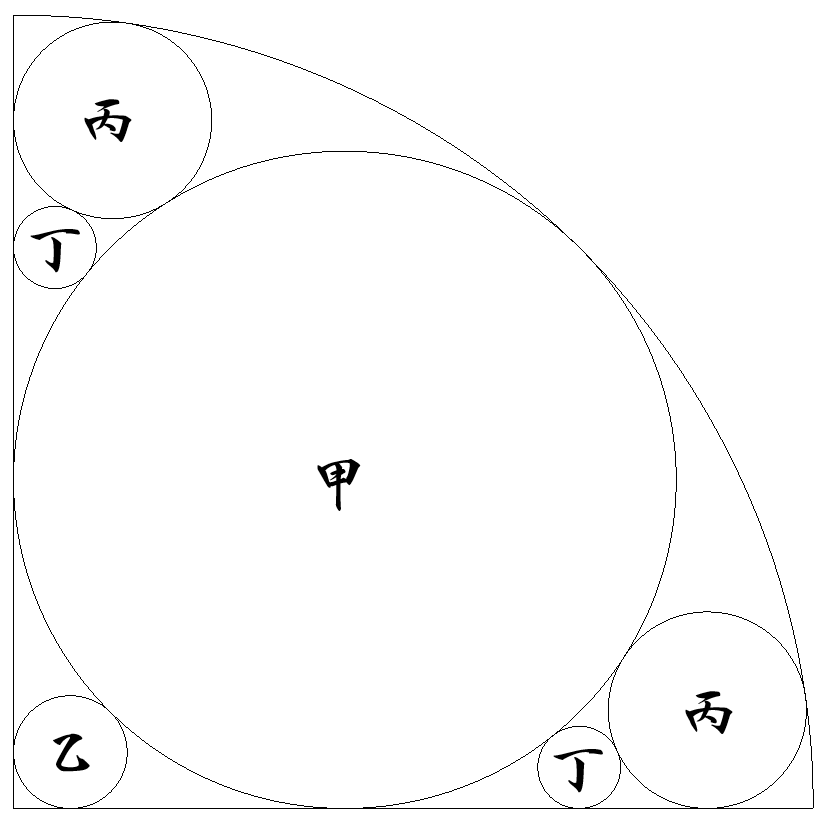



  11. 半径1の半円内に甲乙の5円が図のように内接している。
    各円の半径をそれぞれ求めよ。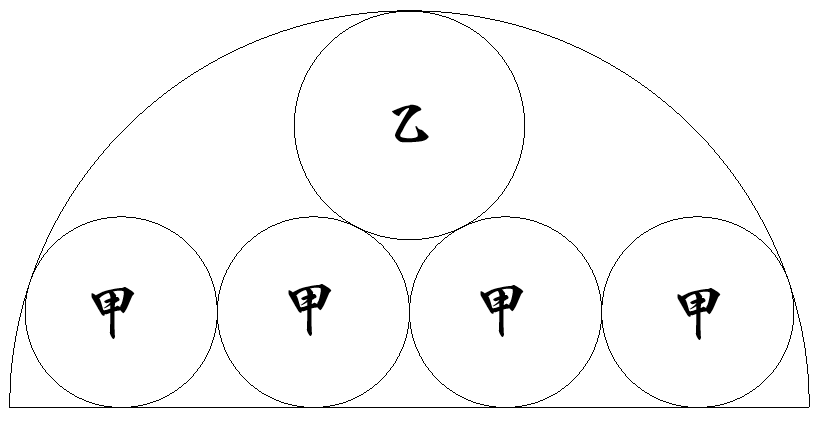



  12. △ABCの垂心Hを3辺に関して対称移動した点H1，H2，H3は，
    三角形の外接円周上にあることを証明せよ。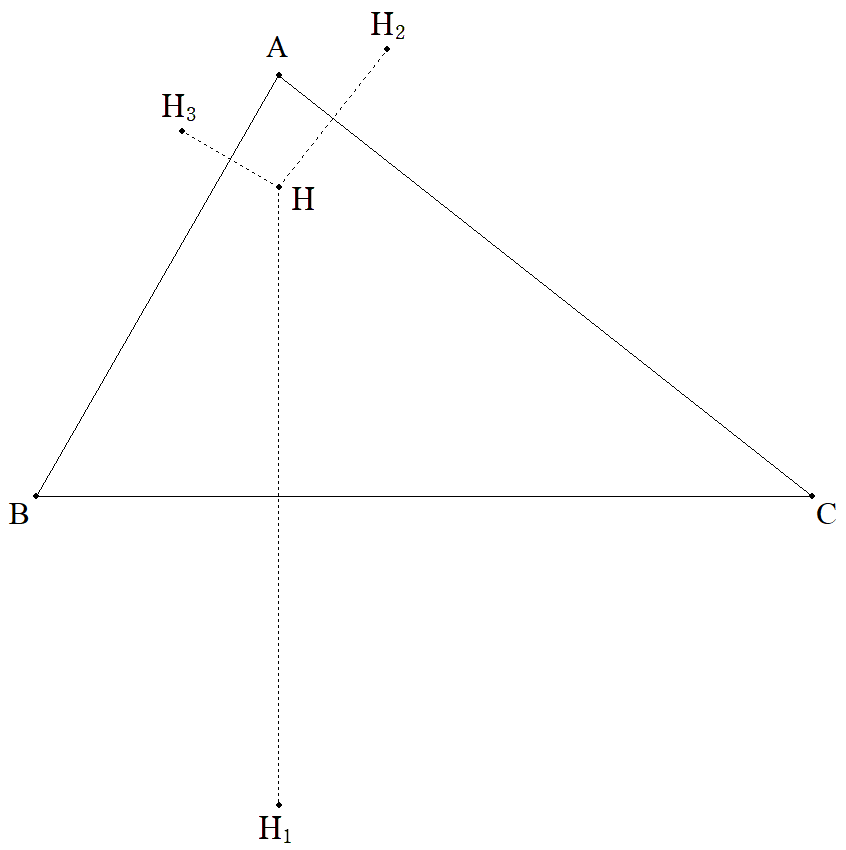



  13. 正方形ABCDのADの延長上に点Eをとり，BC上に点Fを，
    EA＝EFとなるようにとる。また，CDとEFの交点をGとする。
    次を証明せよ。
    (1)　BF＋GD＝FG
    (2)　BF：FC＝CG：2GD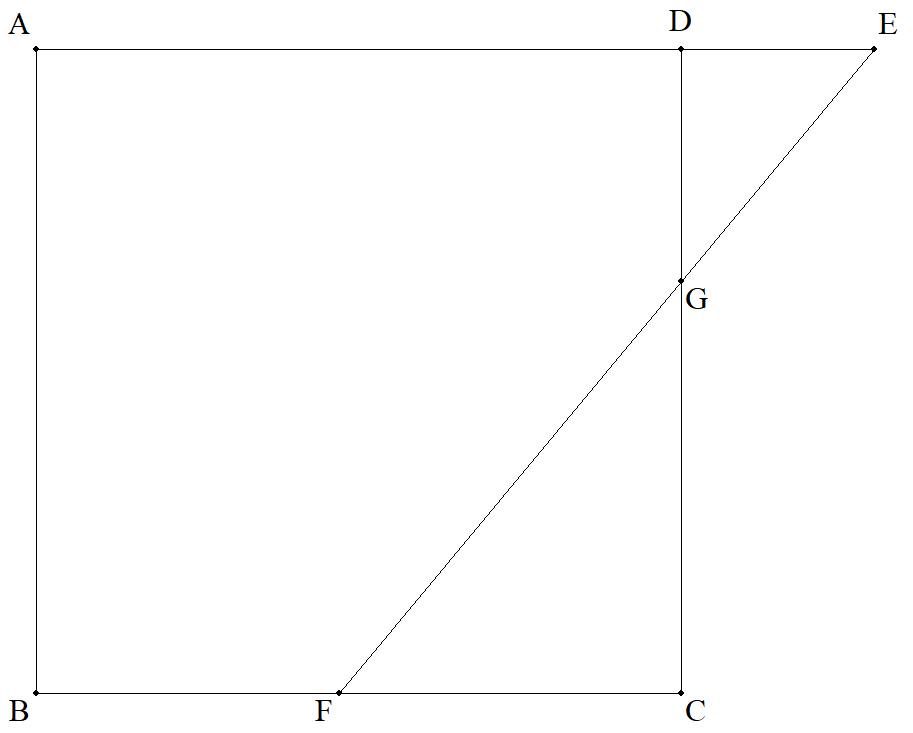






  15. a＞0，b＞0のとき，次の2重根号を外せ。
    √[2√{(a2+b2)-a}√{(a2+b2)-b}]


  16. ∠C＝90°である△ABCのBC，CAを直径とする半円の中心を
    それぞれP，Qとし，半径をそれぞれr1，r2とする。
    半円P，CA，ABに接する円の中心をR，半径をr3，
    半円Q，AB，BCに接する円の中心をS，半径をr4とする。
    ABと円R，Sとの接点をそれぞれD，Eとする。
    次を証明せよ。
    (1)　r1r3＝r2r4
    (2)　AE＝AC，BD＝BC
    (3)　∠DCE＝45°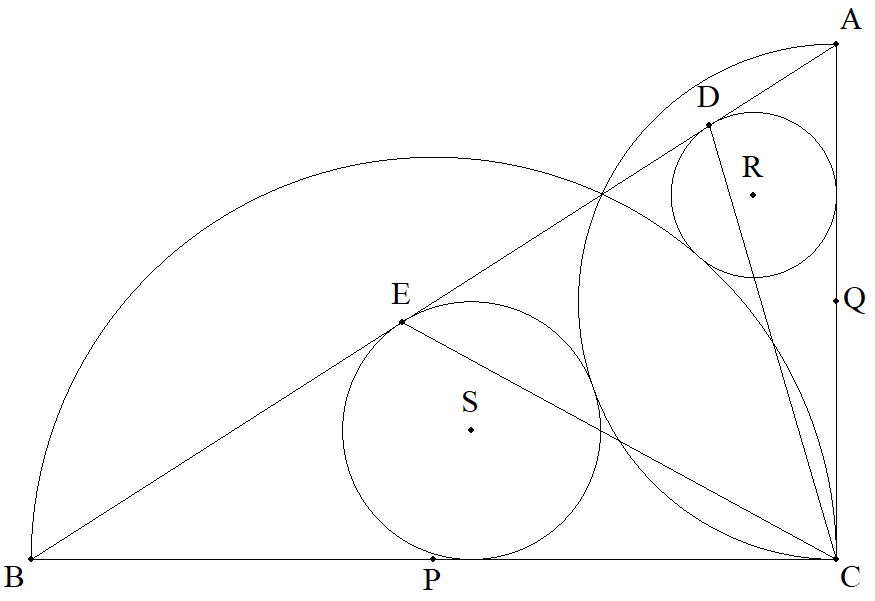



  17. BC＝1＋√2，CA＝1，∠C＝90°である△ABCの3辺を直径とする
    円をそれぞれ描くとき，図の斜線部分の面積の和を求めよ。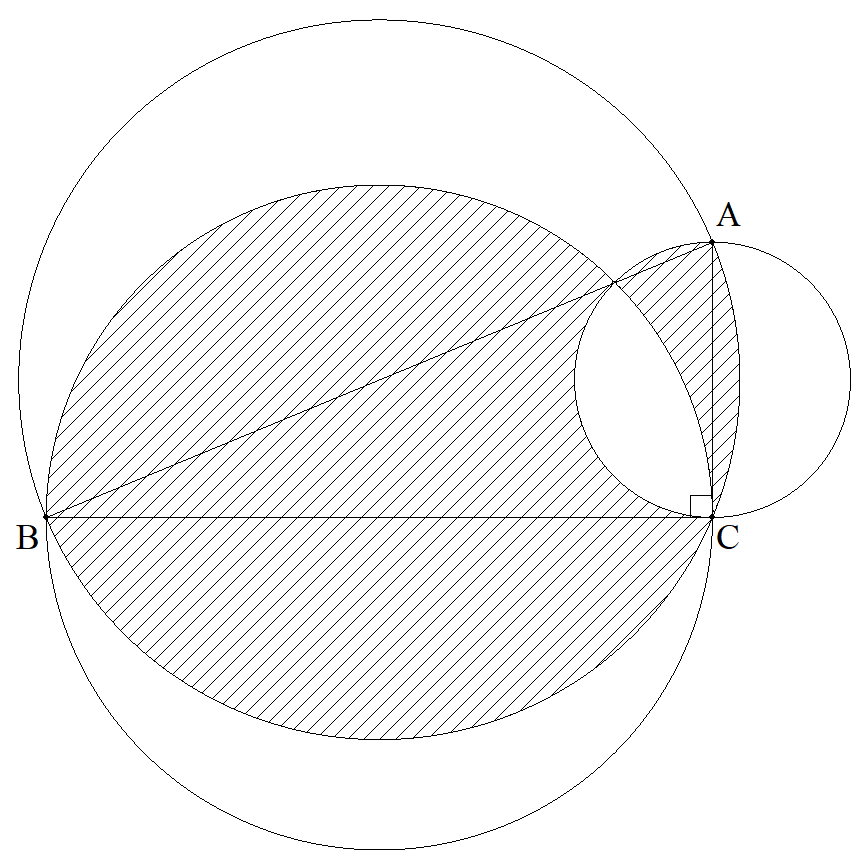



  18. BC=a，CA=b，AB=cである△ABCの外側に各辺を1辺と
    する正方形をつくり，さらに図のように頂点を連結させて
    3個の正方形をつくる。△ABC＝Sとするとき，次の六角形
    の面積をa，b，c，Sを用いて表せ。
    (1)　DEFGHI
    (2)　JKLMNP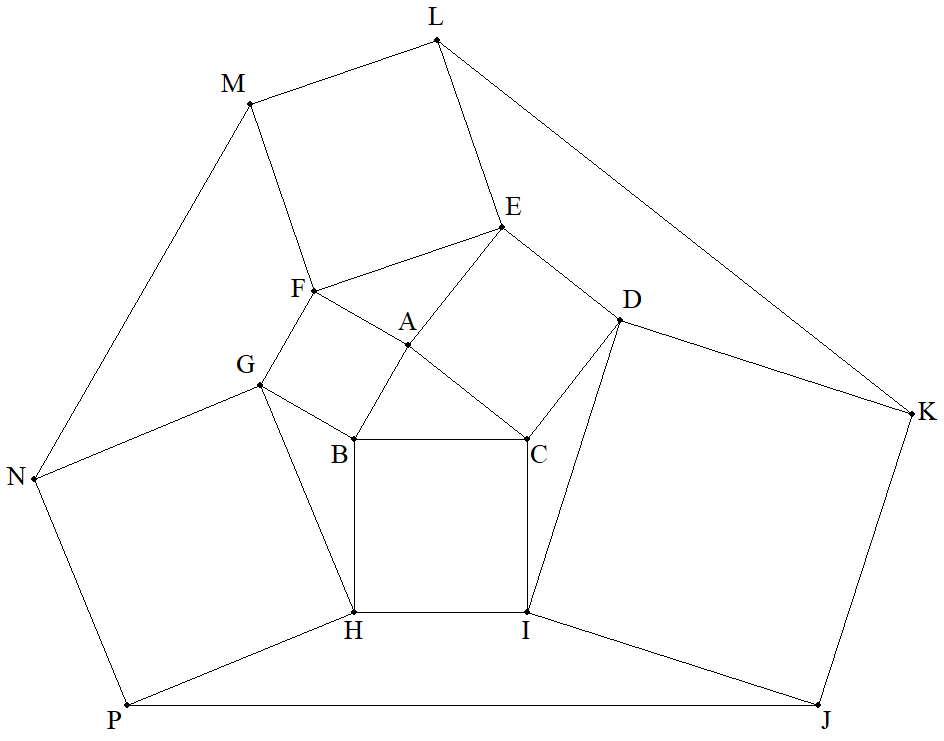



  19. xを超えない最大の整数を[x]で表す。（例）[π]＝3
    また，自然数aをn個つなげた数をa(n)で表す。（例）12(3)＝121212
    このとき，[√4(2n)]の値を求めよ。


  20. BC=a，CA=b，AB=cである△ABCの外側に各辺を1辺と
    する正方形をつくり，さらに図のように頂点を連結させて
    3個の正方形をつくる。このとき，PGを求めよ。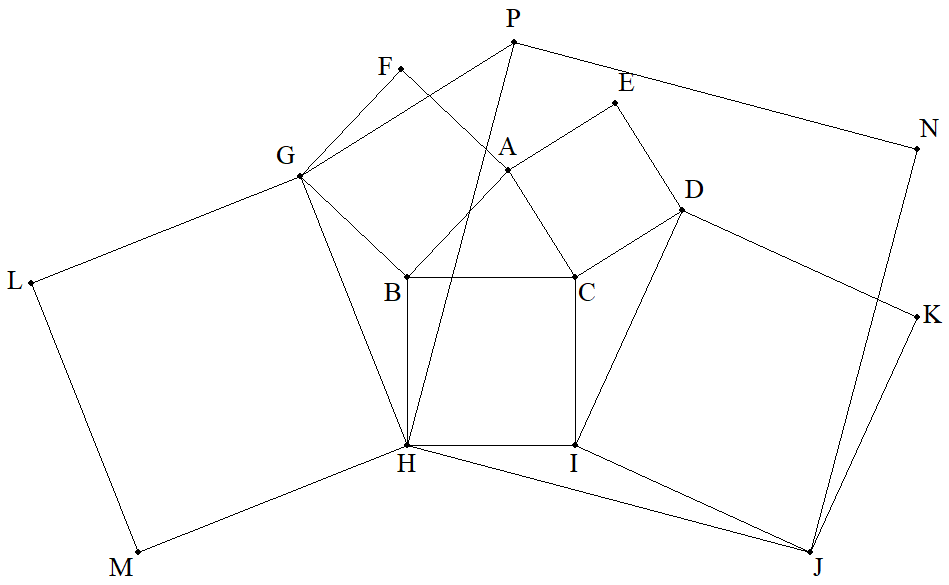



  21. 1辺1の正方形内に，図のように甲乙丙円が接するように
    配置されている。
    各円の半径を求めよ。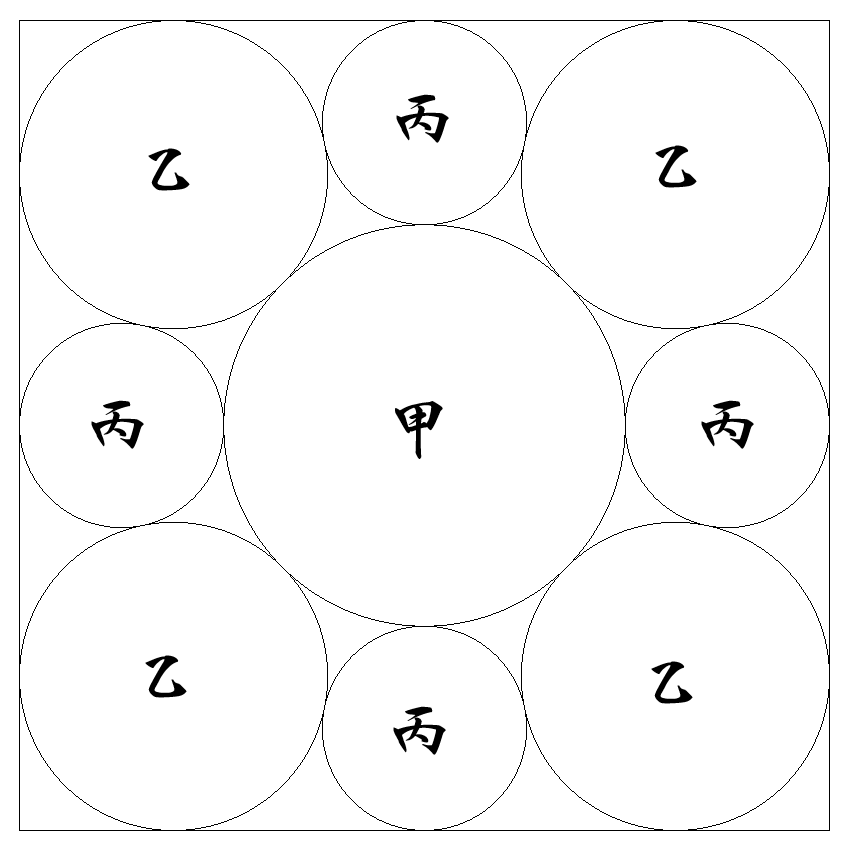



  22. 半径1の甲円内に，図のように乙丙円が甲円と直線に
    接するように配置されている。
    各円の半径を求めよ。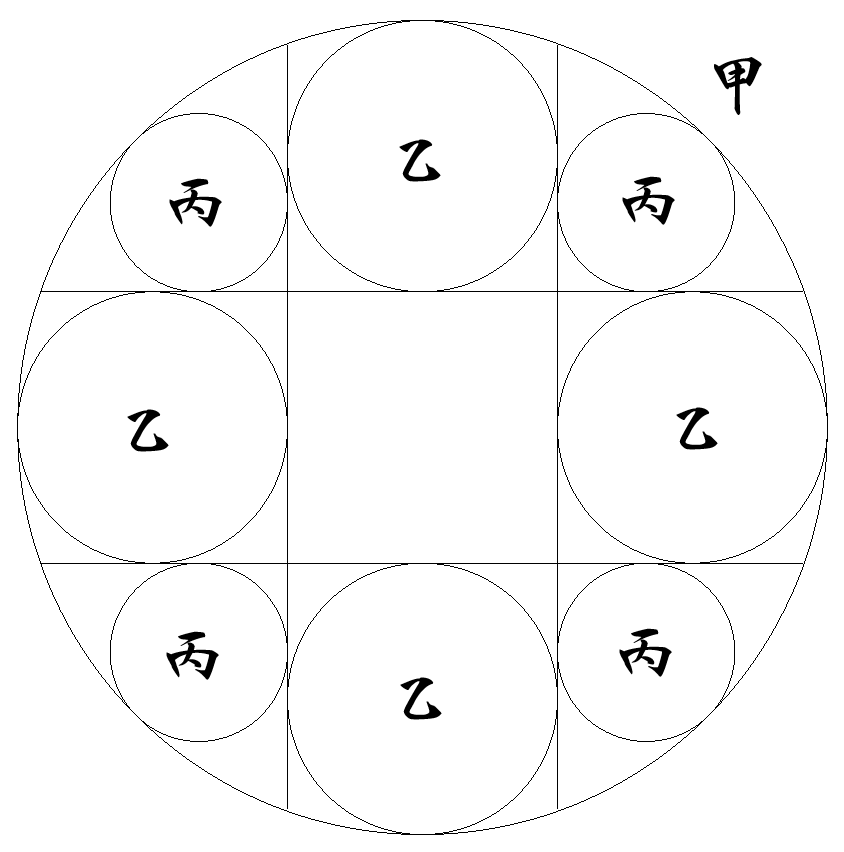



  23. 1辺1の正方形内に，図のように甲乙丙円が接するように
    配置されている。
    各円の半径を求めよ。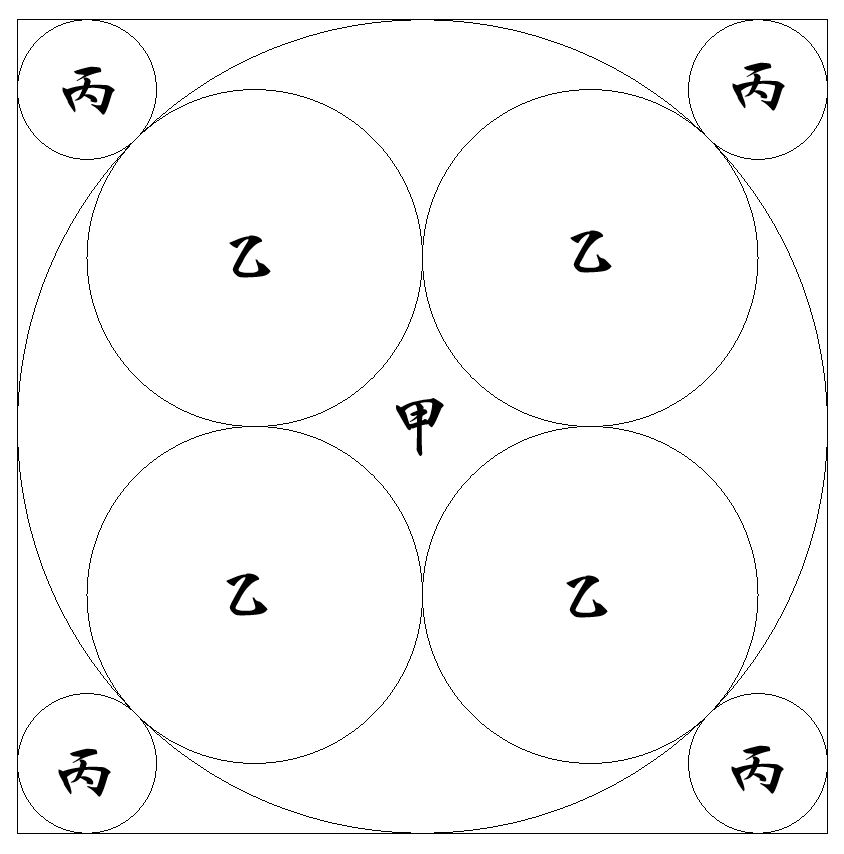



  24. 半径1の甲円内に，正方形が内接しており，図のように乙丙円が
    配置されている。
    各円の半径を求めよ。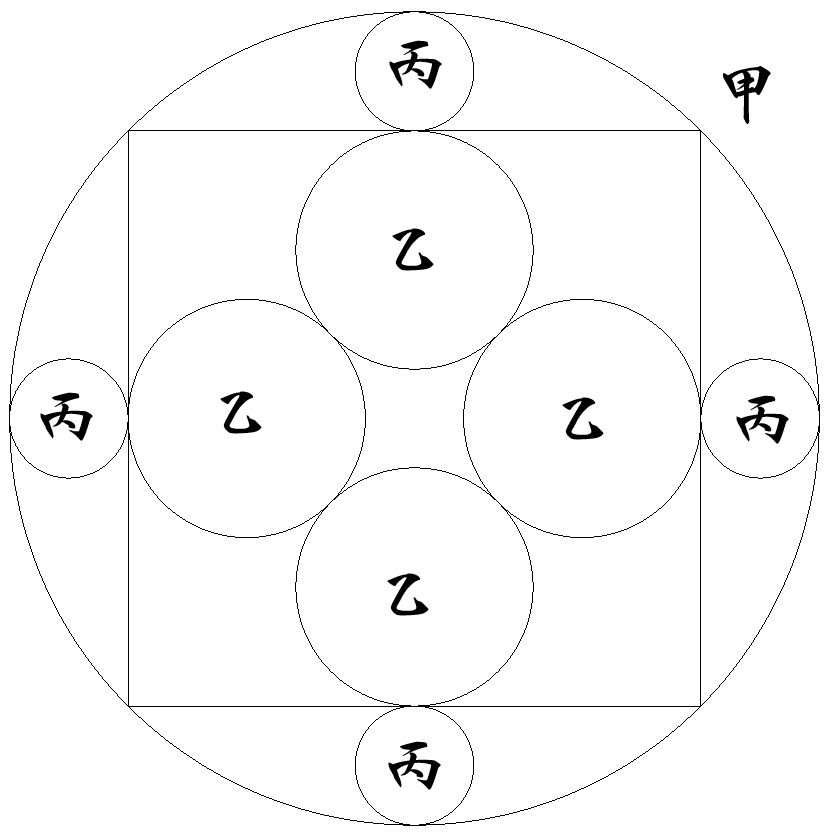



  25. ∠A＝90°，AB＝AC＝2である△ABC内に，図のように
    甲円2個，乙円1個が2辺に接するように配置されている。
    各円の半径を求めよ。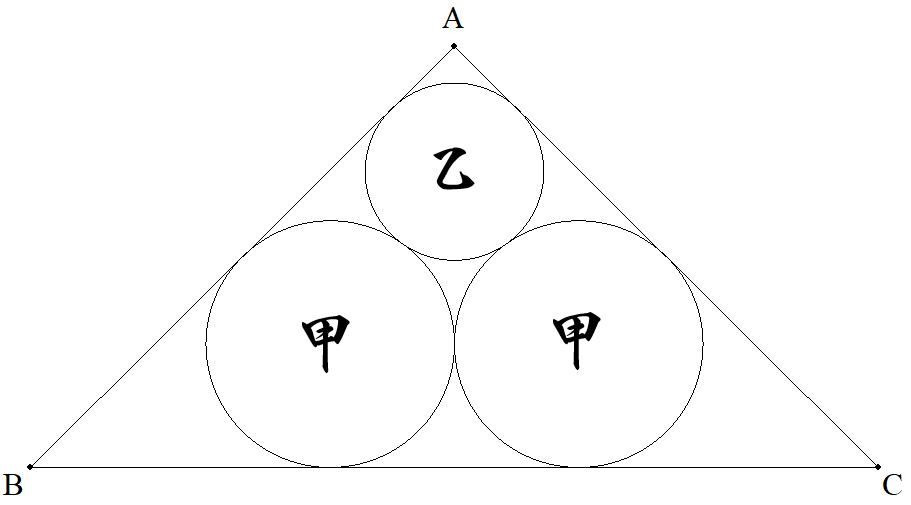



  26. 半径1の4分の1円甲内に半径1/3の4分の1円乙をつくり，
    甲に内接し，乙に外接する半径1/3の半円丙2個をつくる。
    このとき，2個の丙に外接し，甲に内接する円丁の半径を
    求めよ。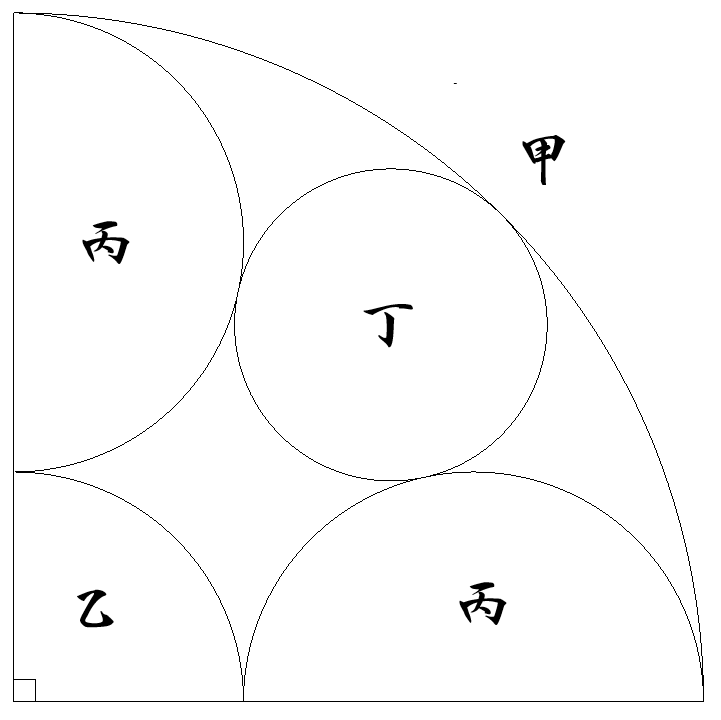



  27. CA=AB=1，∠A＝90°である△ABCのCA，AB上に
    それぞれ点D，EをAD＝AEとなるようにとる。
    このとき，図のように三角形の辺とBD，CEに接する
    2個の円P，Qの半径が等しいとき，その半径を求めよ。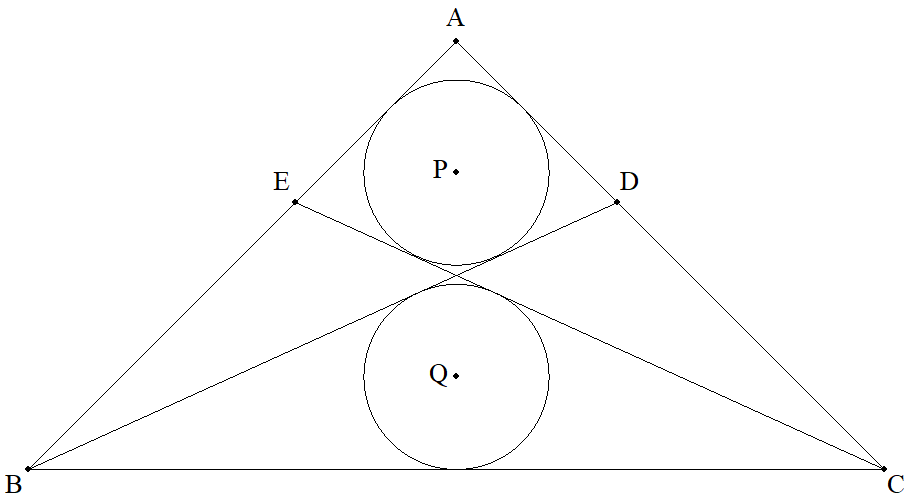



  28. BC＝a（0＜a＜2），CA=AB=1である△ABCのCA，
    AB上にそれぞれ点D，EをAD＝AEとなるようにとる。
    このとき，三角形の辺とBD，CEに接する2円P，Qの
    半径が等しくなるとき，その半径を求めよ。
    また，特にBC＝1のときの半径を求めよ。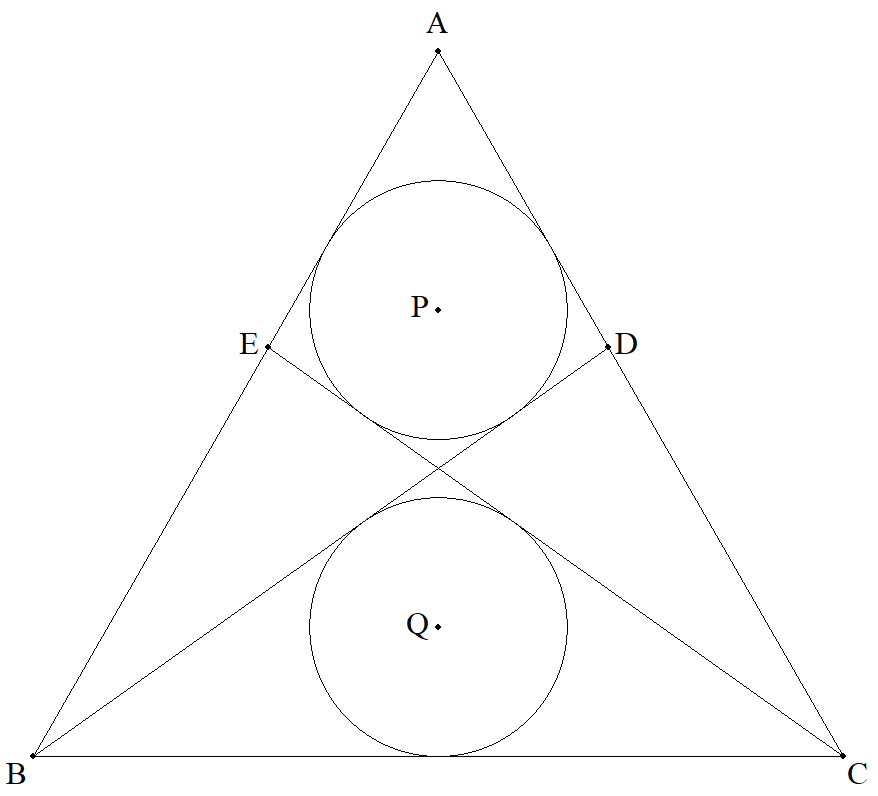



  29. 四角形ABCDはAB＝a，BC＝b，CD＝c，DA＝dで，円に内接している。
    弧AB，BC，CD，DAの中点をそれぞれP，Q，R，Sとする。このとき，
    (1)　四角形ABCDの面積Sをa，b，c，d，(a+b+c+d)/2＝sを用いて
    　　表せ。
    (2)　円の半径Rをa，b，c，d，Sを用いて表せ。
    (3)　四角形PQRSの面積S´をa，b，c，d，Sを用いて表せ。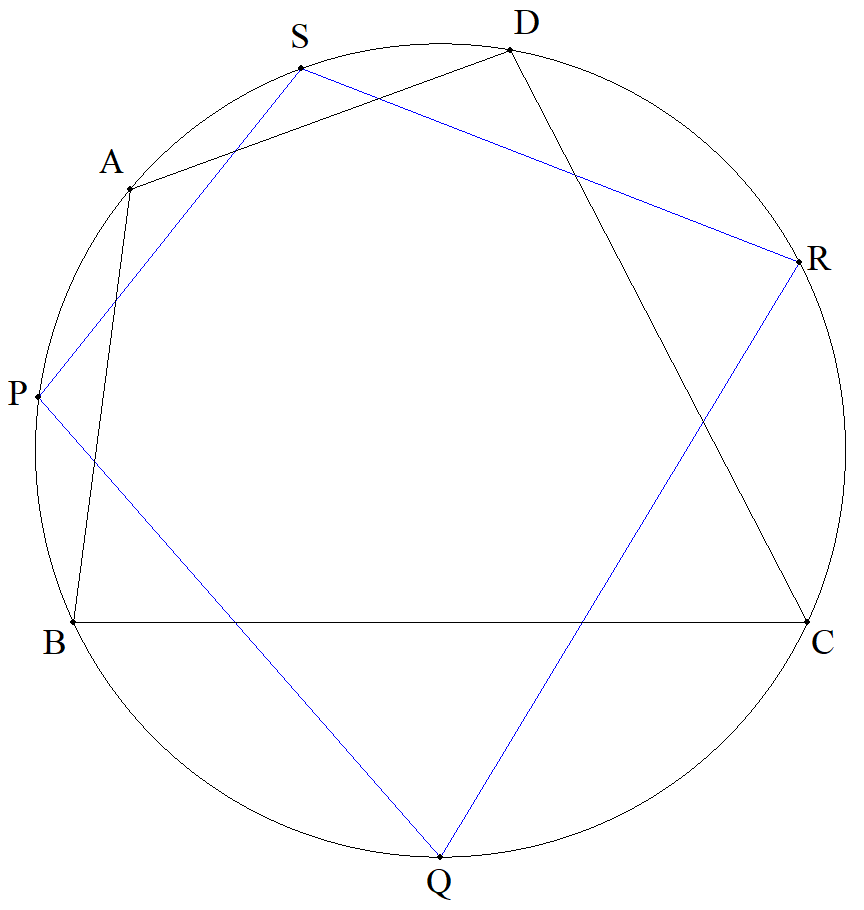



  30. 正方形9個が図のように連結している。
    赤の正方形の1辺が1のとき，黄の正方形の1辺を求めよ。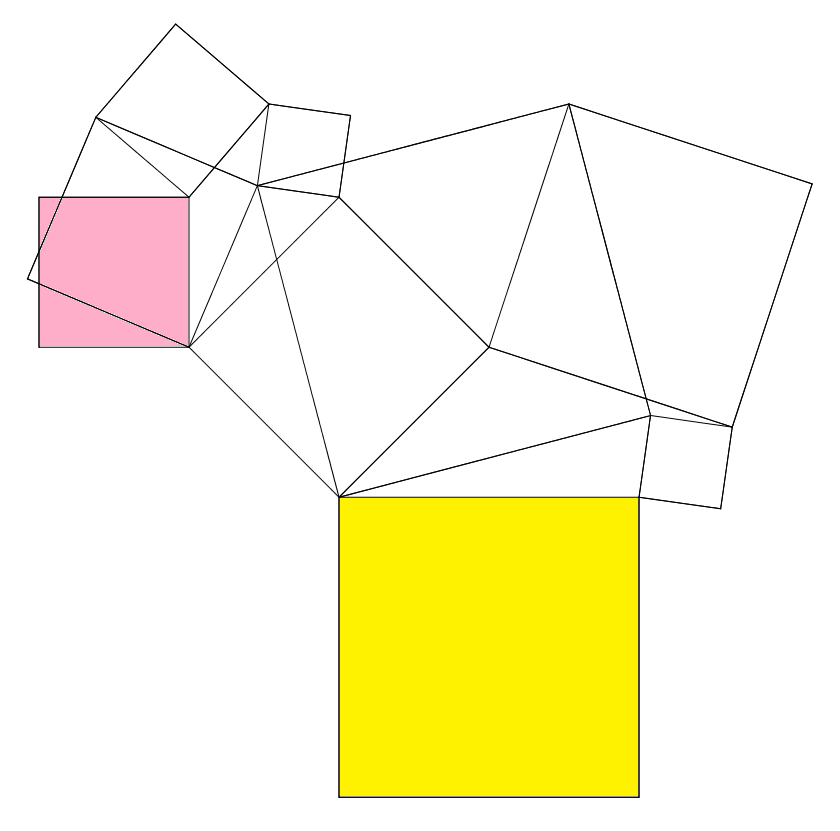



  31. 四角形ABCDの内部に点P，Qをとり，△PAB，△PCD，△QBCが，
    直角二等辺三角形になるとき，△QDAも直角二等辺三角形になる
    ことを証明せよ。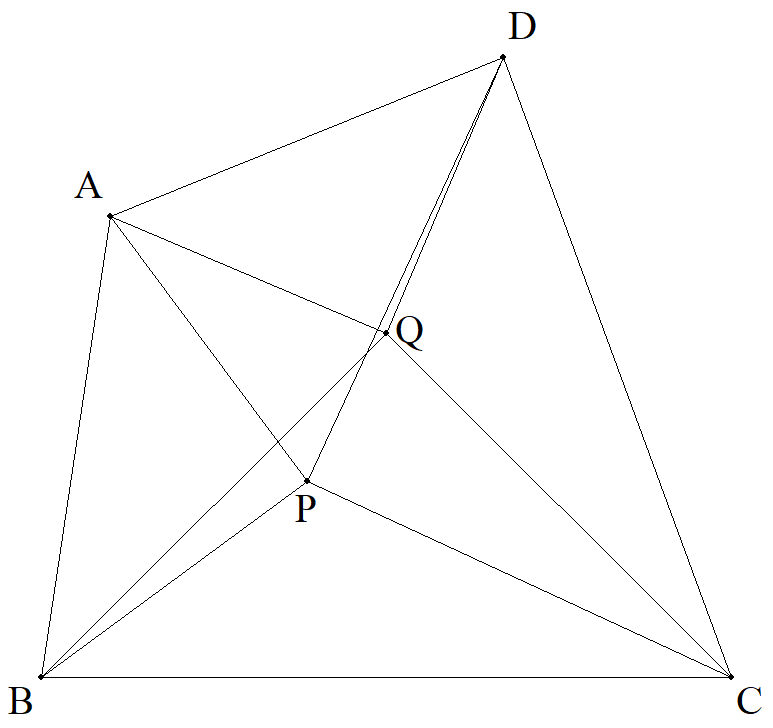



  32. 面積がS1，S2，S3，S4である4個の正方形が
    図のように配置されているとき，
    S1＋S4＝2(S2＋S3)を証明せよ。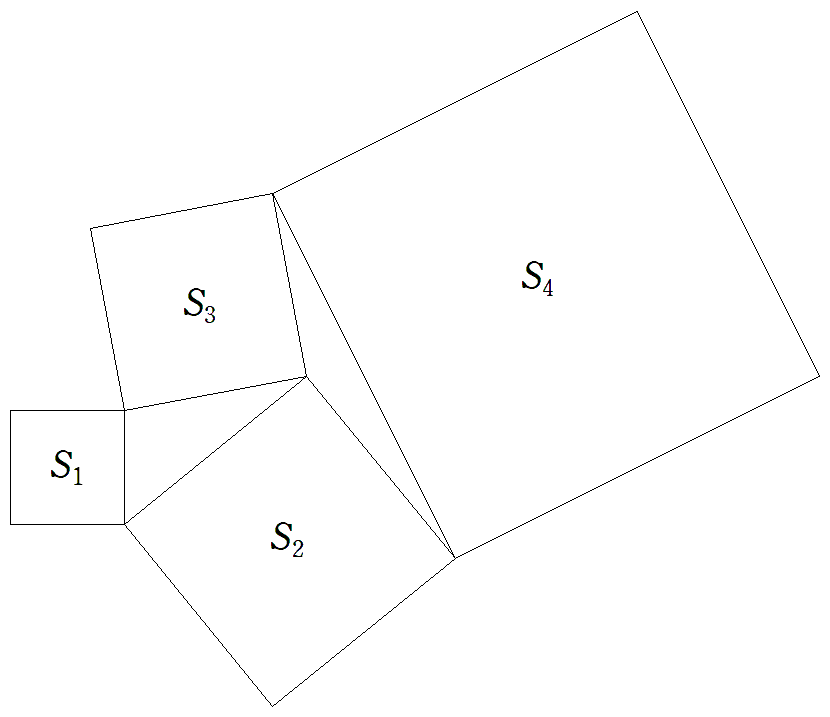



  33. 正方形11個が図のように配置されている。
    赤，青，黄の面積がそれぞれ2，3，4のとき，
    茶と黄緑の面積を求めよ。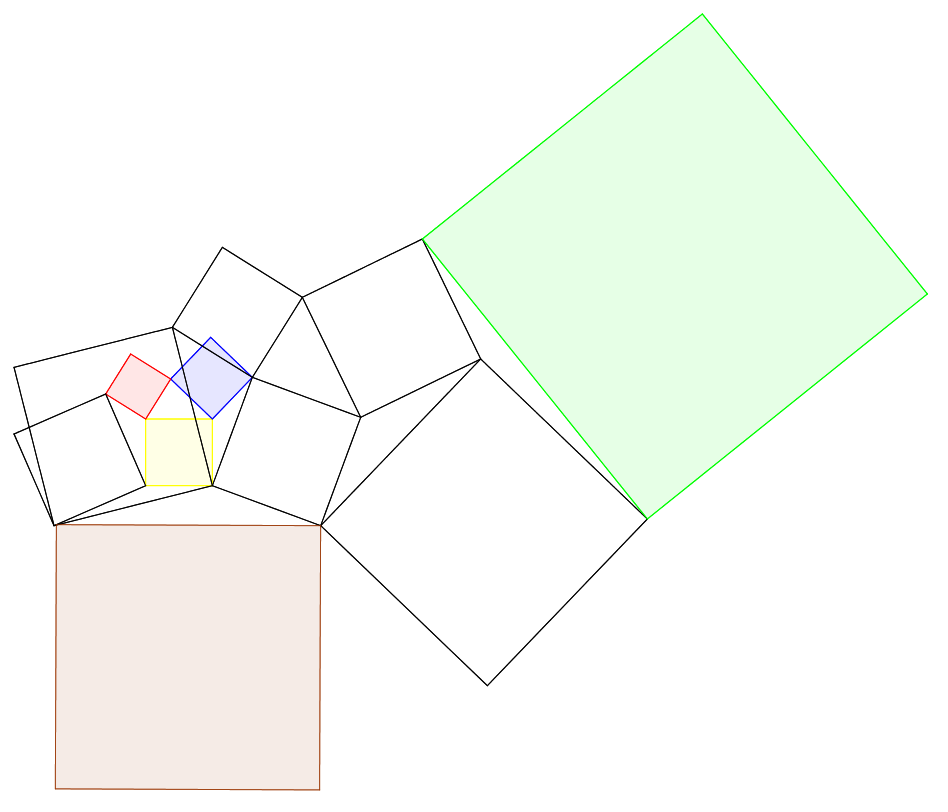



  34. AB=3，∠B＝45°，∠C＝30°である△ABCの内心をIとする。
    BIとCAの交点をDとするとき，BI・BDの値を求めよ。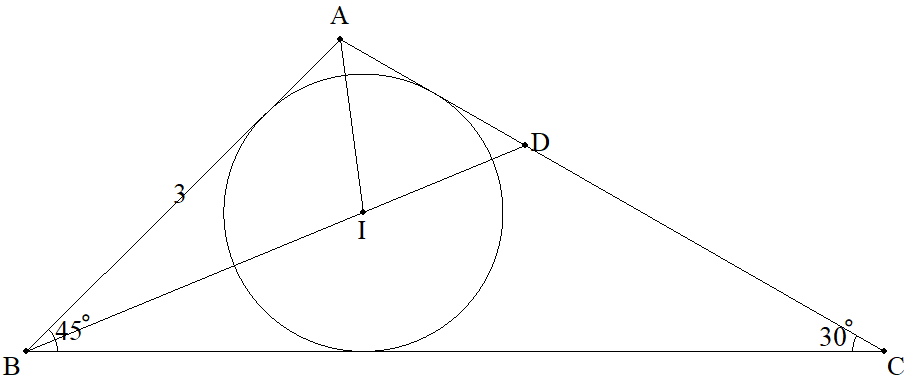



  35. ∠A＝60°である△ABCの垂心をHとする。
    BHとCAの交点をD，CHとABの交点を
    Eとすると，∠CHDの二等分線は△ABCの
    外心を通ることを証明せよ。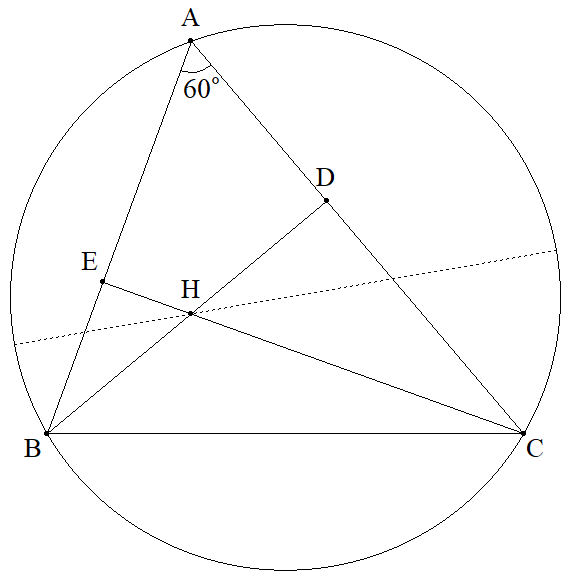



  36. 11個の正方形が図のように配置されている。
    赤，青，黄の面積がそれぞれ2，3，4のとき，
    緑の面積を求めよ。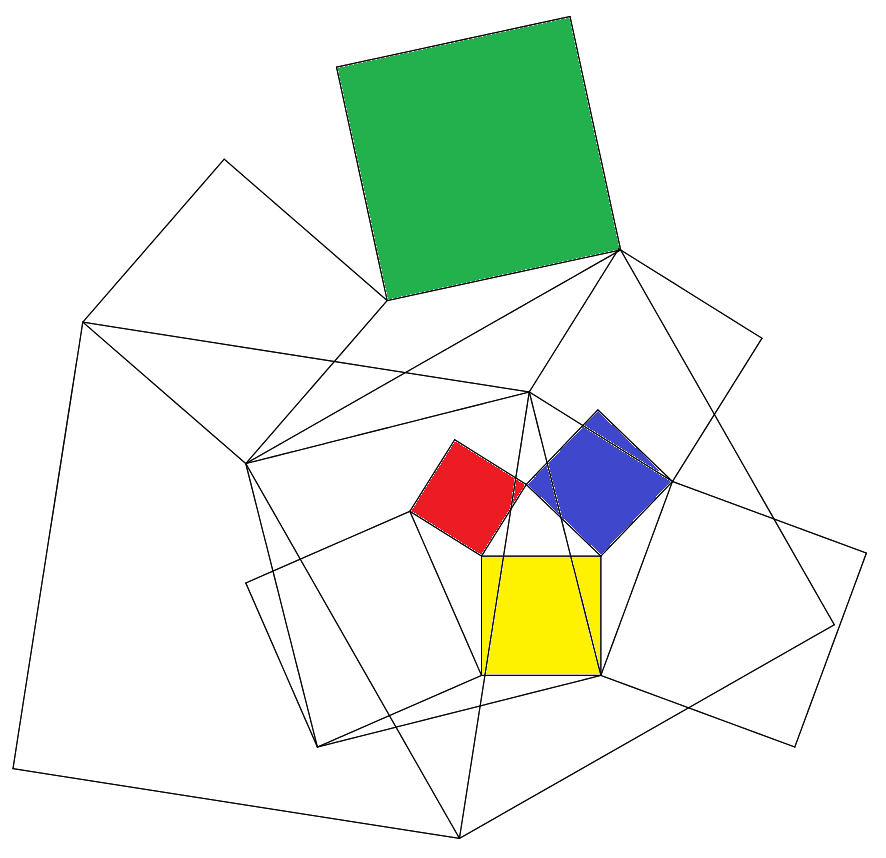



  37. √(44…488…89)の整数部分を求めよ。
    ただし，根号の中は，4を2020個並べた後に8を2019個並べ，最後に9を並べた4040桁の数である。



  38. 長方形内に図のように4個の正方形が配置されている。
    図に示された2か所の長さから，4個の正方形の面積を
    それぞれ求めよ。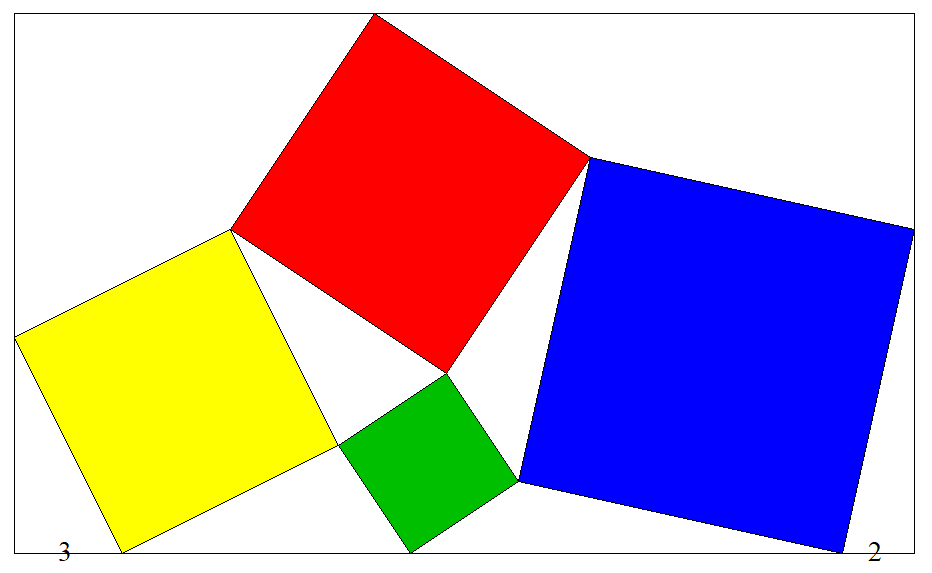



  39. 11個の正方形A，B，…，Kが図のように配置されている。
    A，B，Cの面積がそれぞれ2，3，4のとき，Kの面積を求めよ。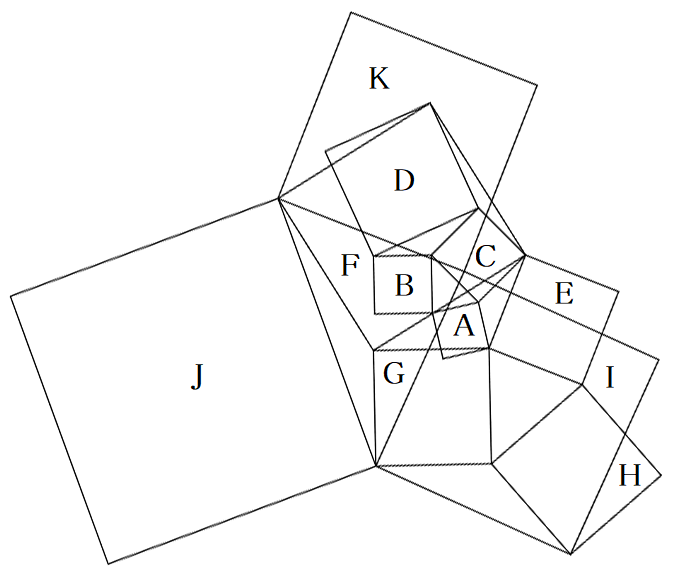



  40. 半径1の大円に，図のように甲円3個，
    乙円1個が左右対称に配置されている。
    （左右の甲円は弦の中点で接している）
    甲円，乙円の半径をそれぞれ求めよ。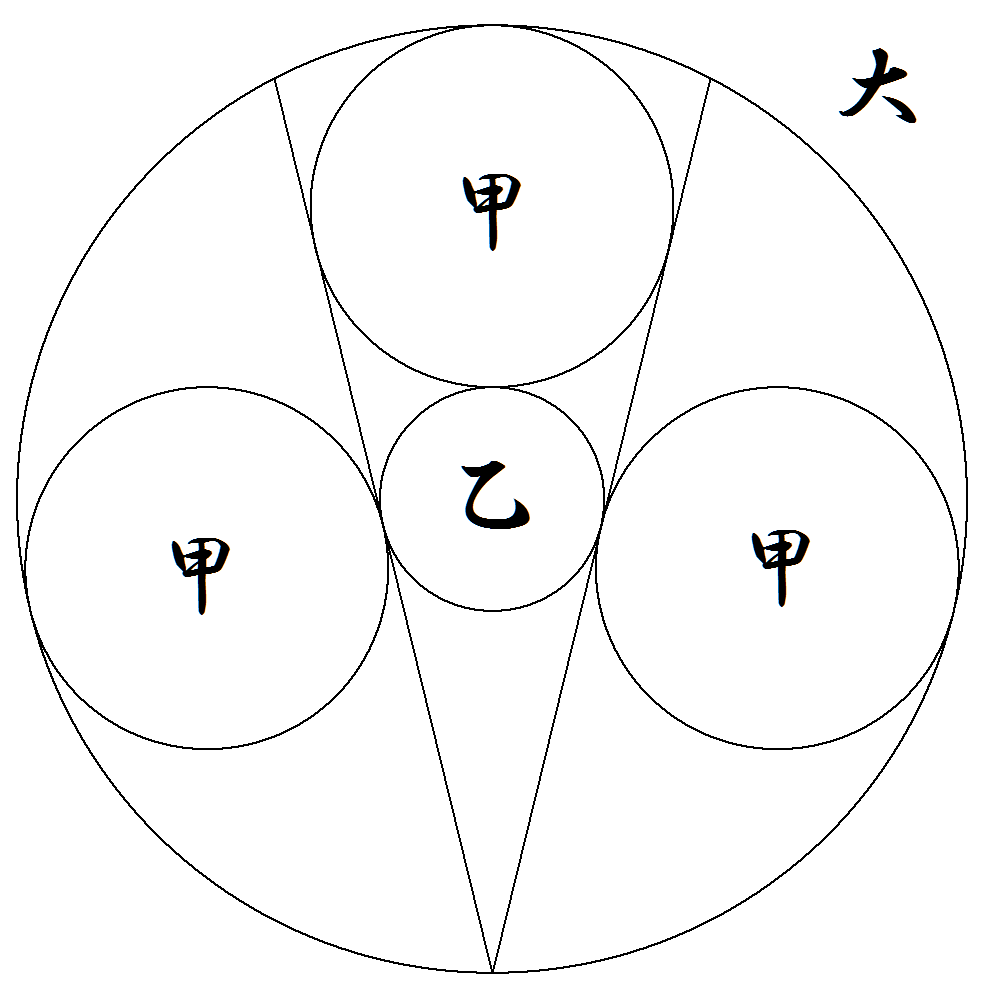



  41. ABを直径とする円周上に点CをBC>CAとなるようにとり，
    さらに，ABを直径とする円周上に点DをCA=CDとなるよ
    うにとる。
    BCの中点Mを通り，ABに平行な直線と直線CDの交点Eが
    BCを直径とする円周上にあるとき，∠ACDを求めよ。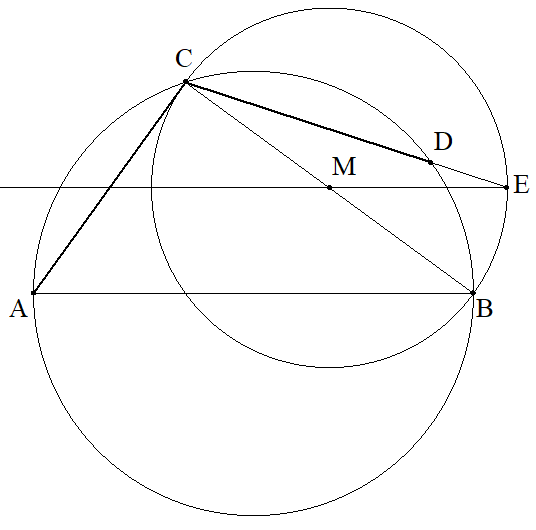



  42. CA=AB=a，BC=b(a＞2b)である△ABCの内心をI，垂心をH，
    頂点と内接円と対辺の接点を結んだ線分の交点をG(Gergonne点)，
    頂点と傍接円と対辺の接点を結んだ線分の交点をN(Nagel点)とする。
    このとき，NI：IG：GHを求めよ。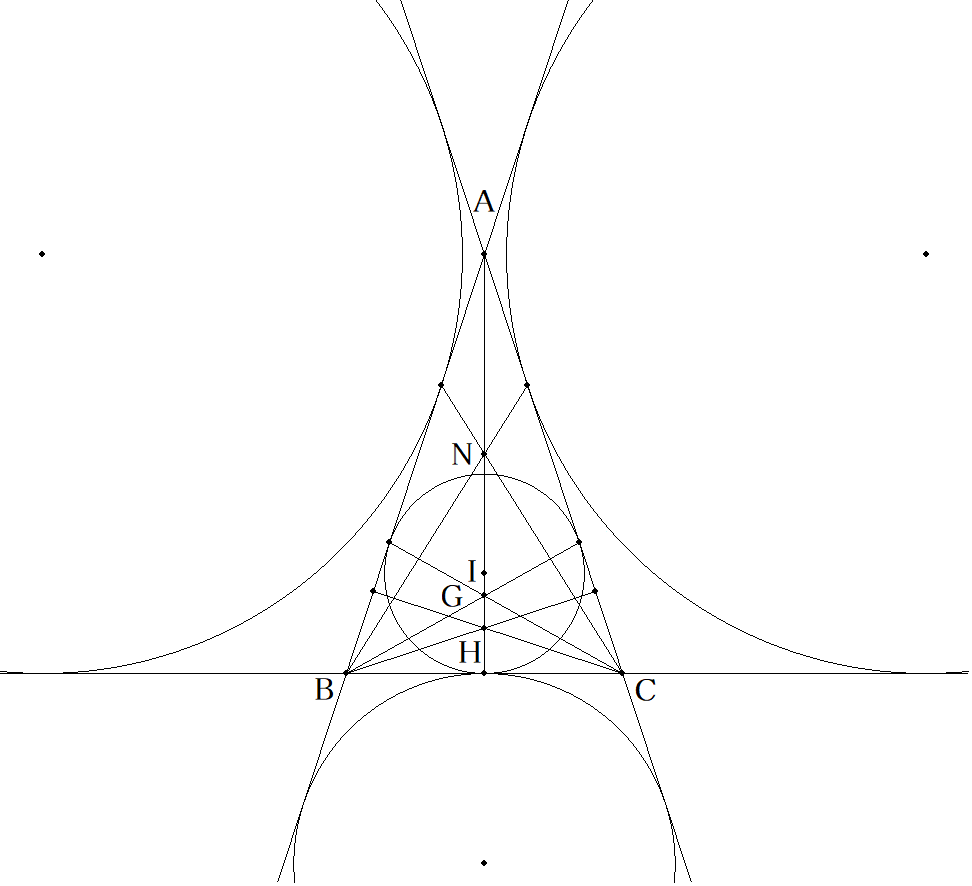



  43. △ABCの外側に正方形ADEB，CFGAをつくり，EF
    とAB，ACとの交点をそれぞれH，Iとする。
    BC＝a，CA＝b，AB＝c，△ABC＝S，△AHI＝S1，
    △BHE＝S2，△CFI＝S3とするとき，S1，S2，S3，
    をa，b，c，Sを用いて表せ。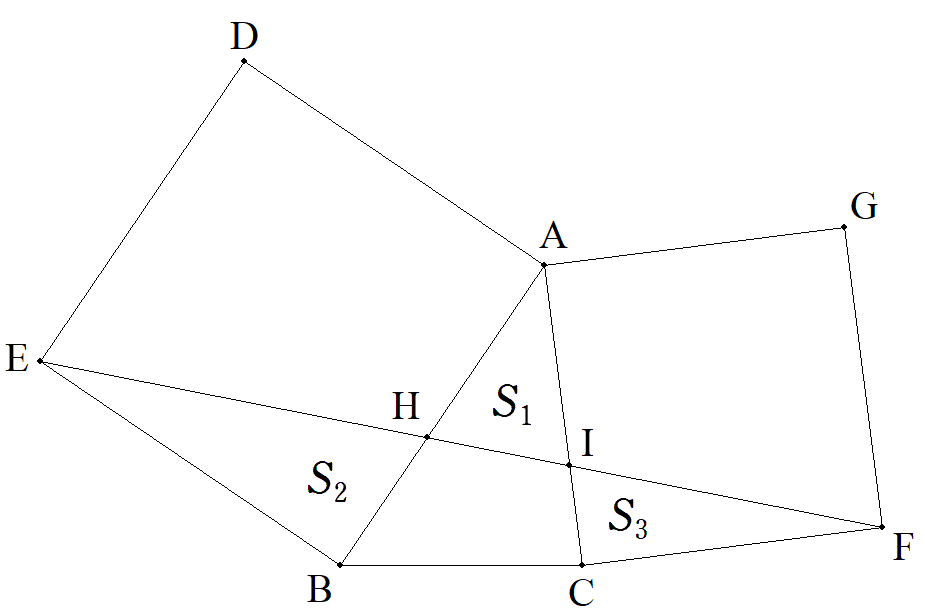



  44. nは5以上の整数とする。
    正n角形A1A2…An内にn個の点P1，P2，…，Pnを△A1A2P1，
    △A2A3P2，…，△AnA1Pnが合同になるようにとる。A1P1の
    長さが最大になるとき，∠P1A1A2の大きさを求めよ。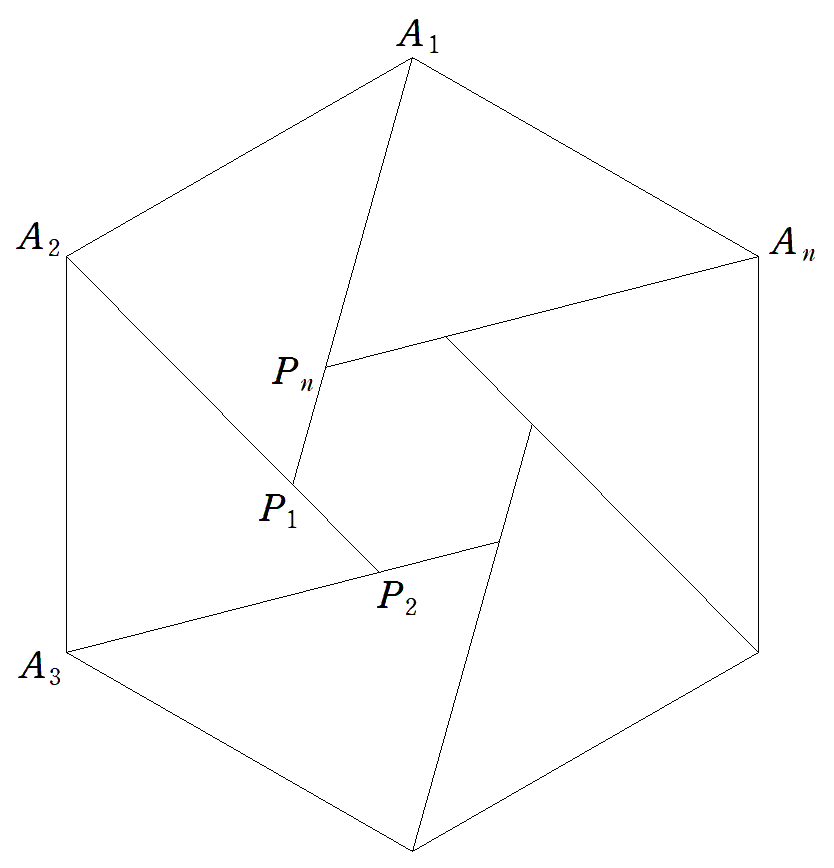



  45. 6個の正方形が図のように配置されている。
    3個の三角形赤，青，黄の面積がそれぞれ
    1，3，5であるとき，緑の正方形の面積を
    求めよ。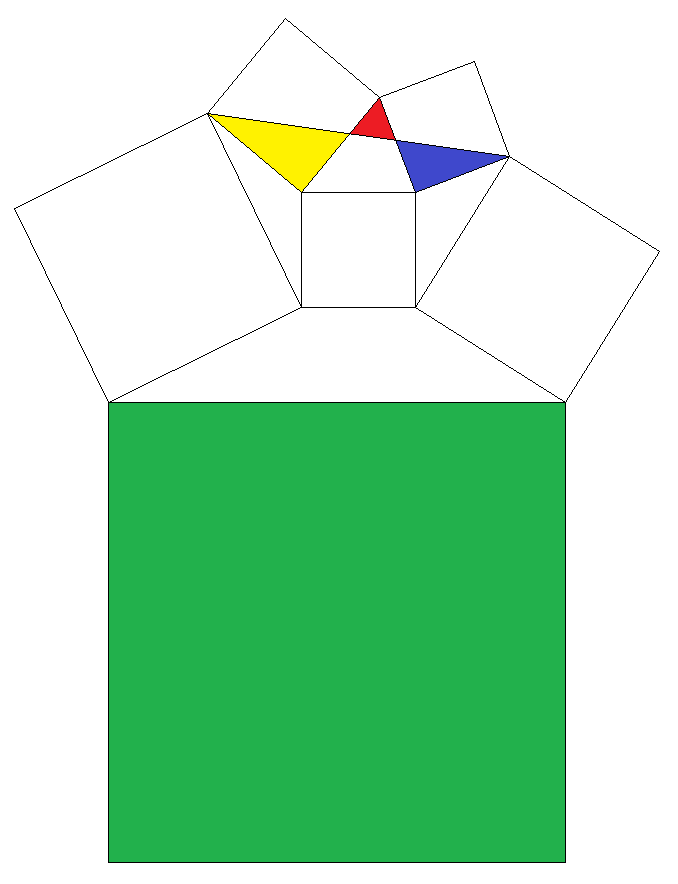



  46. △ABCの外側に正方形AA1B2B，BB1C2C，CC1A2Aを
    つくり，C1A2とA1B2の交点をA′，A1B2とB1C2の交点
    をB′，B1C2とC1A2の交点をC′とする。
    BC＝a，CA＝b，AB＝c，△ABC＝Sとするとき，
    △A′B′C′の面積を求めよ。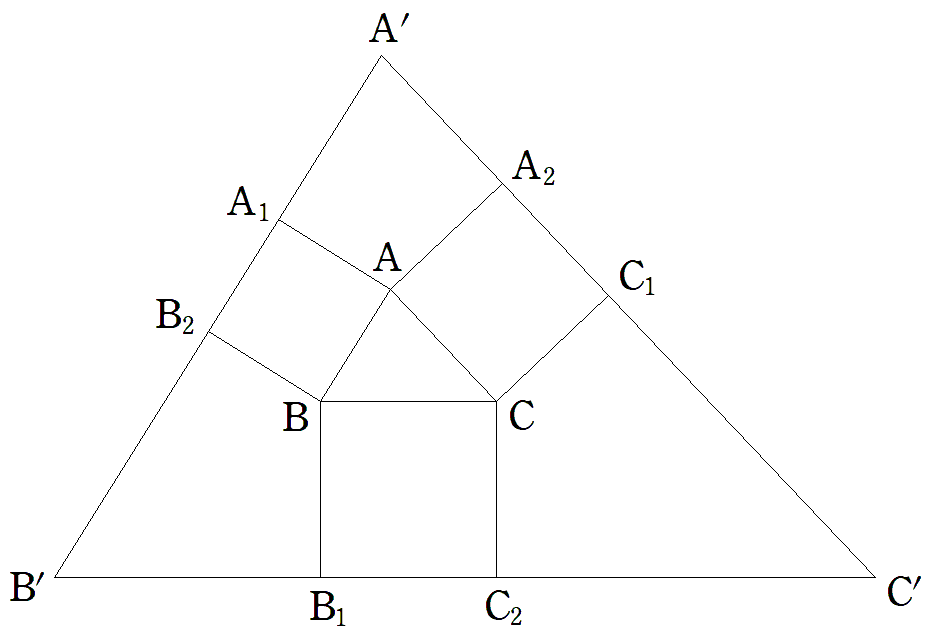



  47. 円に内接する四角形ABCDの外側に正方形
    AA1B2B，BB1C2C，CC1D2D，DD1A2Aをつくり，
    直線D1A2と直線A1B2の交点をA′，
    直線A1B2と直線B1C2の交点をB′，
    直線B1C2と直線C1D2の交点をC′，
    直線C1D2と直線D1A2の交点をD′とする。
    このとき，
    (1)　四角形ABCDの面積Sを，AB＝a，BC＝b，CD＝c，
    　　DA＝d，s＝(a+b+c+d)/2を用いて表せ。
    (2)　四角形A′B′C′D′の面積S′を，a，b，c，d，S
    　　を用いて表せ。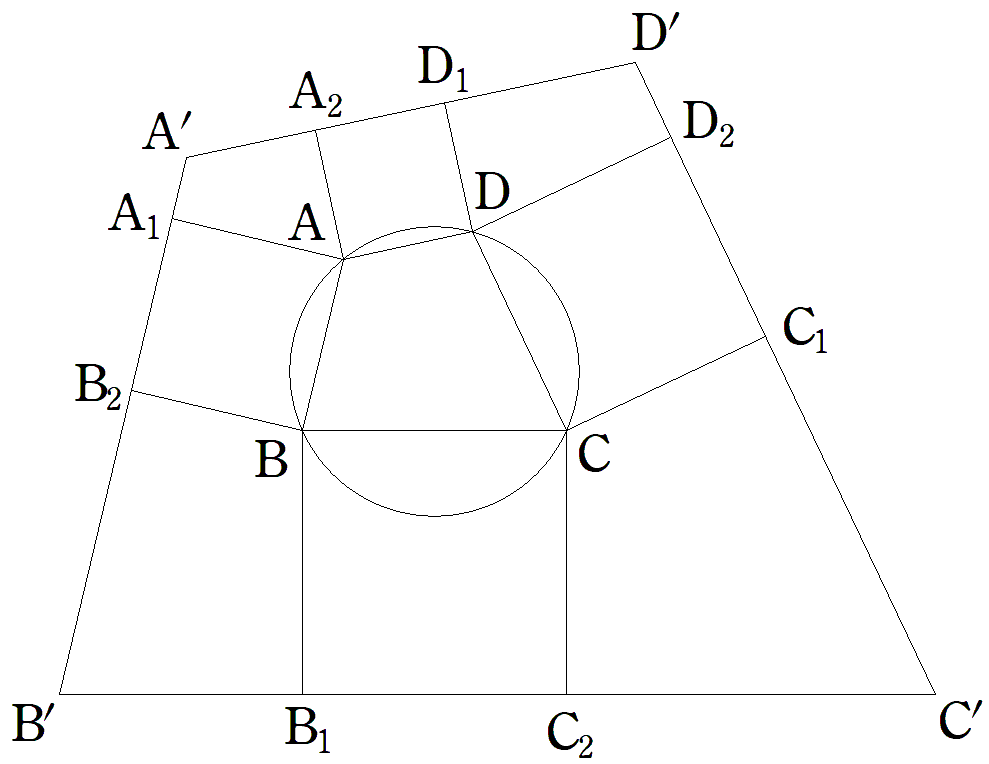



  48. 四角形ABCDは円に内接し，AB＝4，BC＝6，
    CD＝5，DA＝3である。
    その四角形の外側に正方形AEFB，BGHC，CIJD，
    をつくり，さらに図のように正方形FKLG，HMNI
    をつくる。
    このとき，LMを1辺とする正方形の面積を求めよ。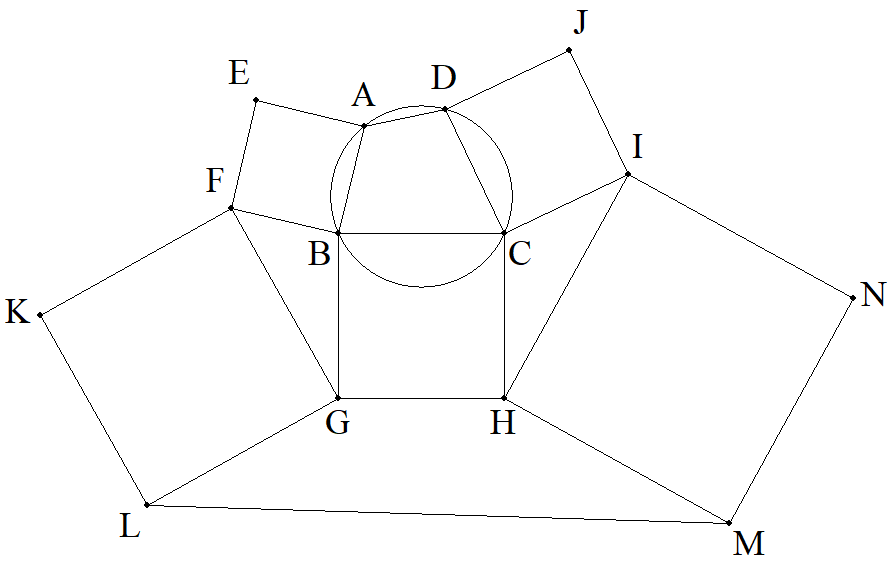



  49. (1+x7+x13)100を展開したとき，いくつの項が現れるか。



  50. 四角形ABCDについて，BC＝b≠DA，CD＝c≠AB，
    ∠DAB＝A，∠ABC＝∠CDA＝90°のとき，
    (1)　AB，ADを求めよ。
    (2)　四角形ABCDの面積Sを求めよ。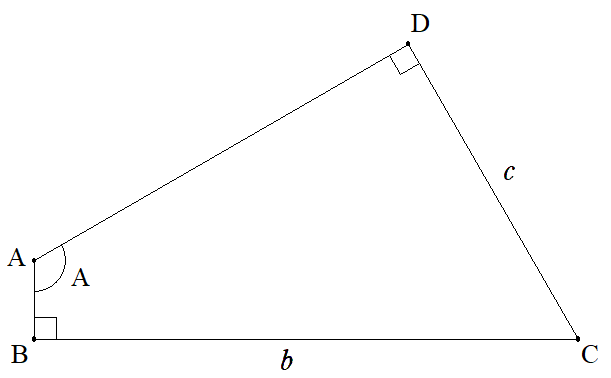