趣味の数学問題集・Ａ問題

■趣味の数学問題集・Ａ問題

円に内接する五角形ABCDEの外側に各辺を1辺
とする正方形をつくり，図のように，それらを
取り囲む五角形A′B′C′D′E′をつくる。
EA＝AB＝5，BC＝CD＝DE＝6のとき，
(1)　五角形ABCDEの面積Sを求めよ。
(2)　五角形A′B′C′D′E′の面積S′を求めよ。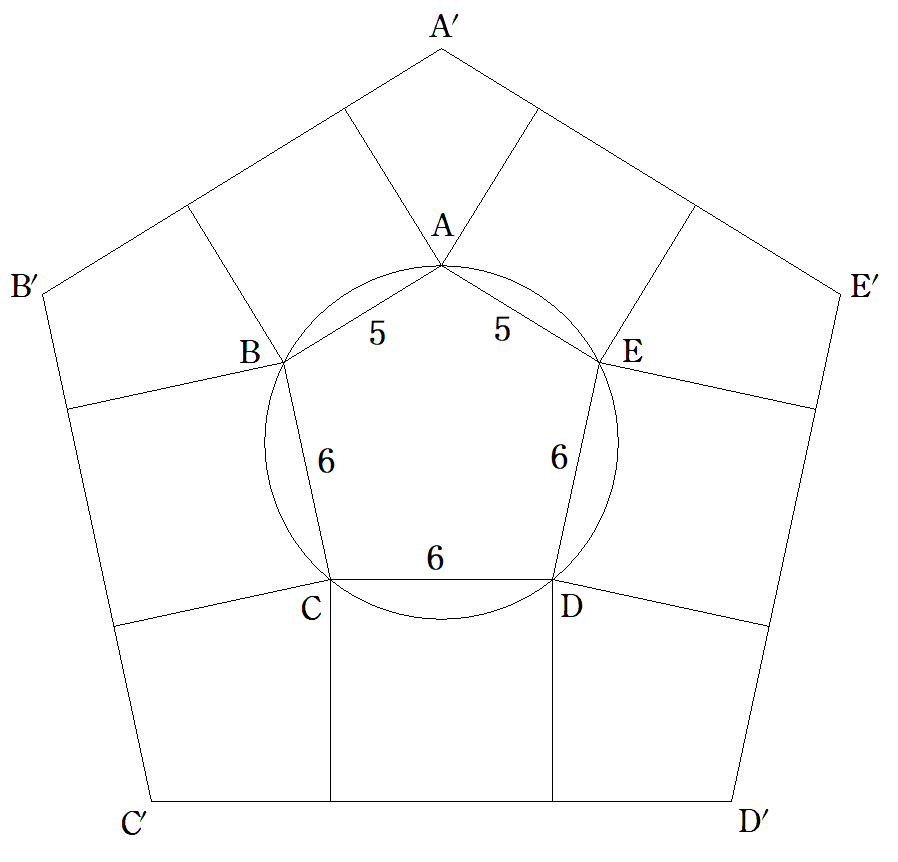

円に内接する五角形ABCDEの外側に各辺を1辺
とする正方形をつくり，図のように，それらを
取り囲む五角形A′B′C′D′E′をつくる。
EA＝AB＝3，BC＝CD＝DE＝2のとき，
(1)　五角形ABCDEの面積Sを求めよ。
(2)　五角形A′B′C′D′E′の面積S′を求めよ。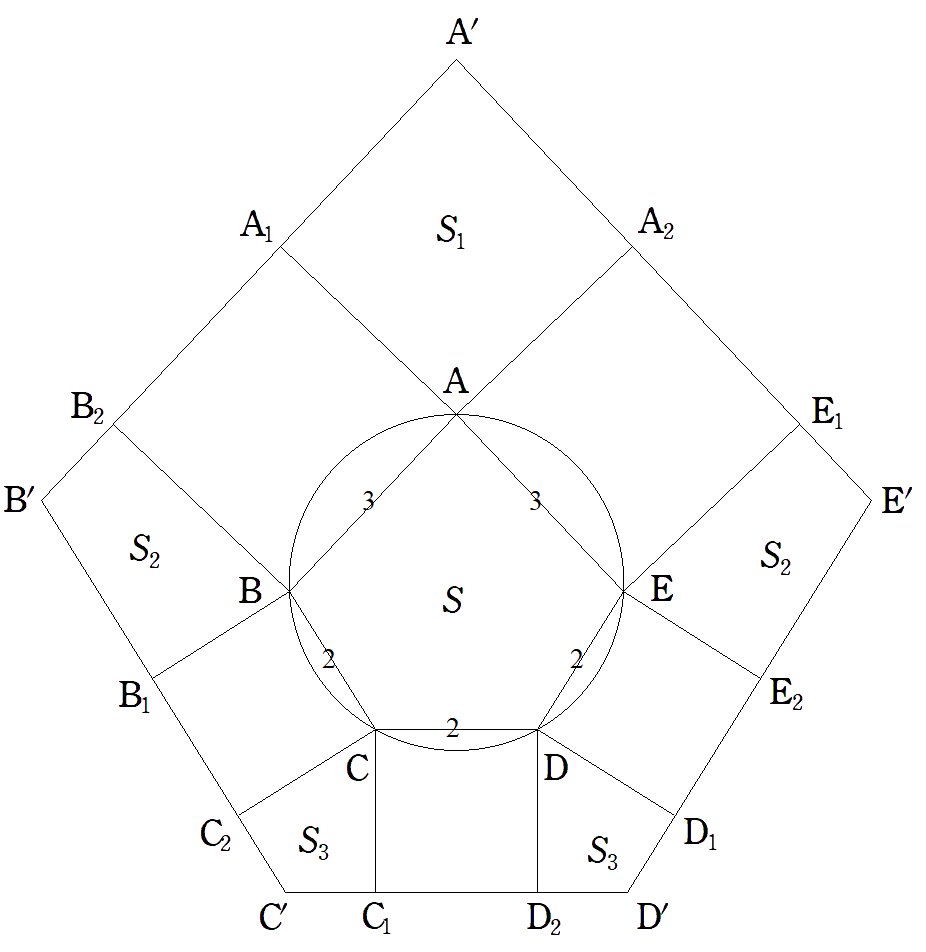

円に内接する五角形ABCDEの外側に各辺を1辺
とする正方形をつくり，図のように，それらを
取り囲む五角形A′B′C′D′E′をつくる。
EA＝AB＝7，BC＝CD＝DE＝12のとき，
(1)　五角形ABCDEの面積Sを求めよ。
(2)　五角形A′B′C′D′E′の面積S′を求めよ。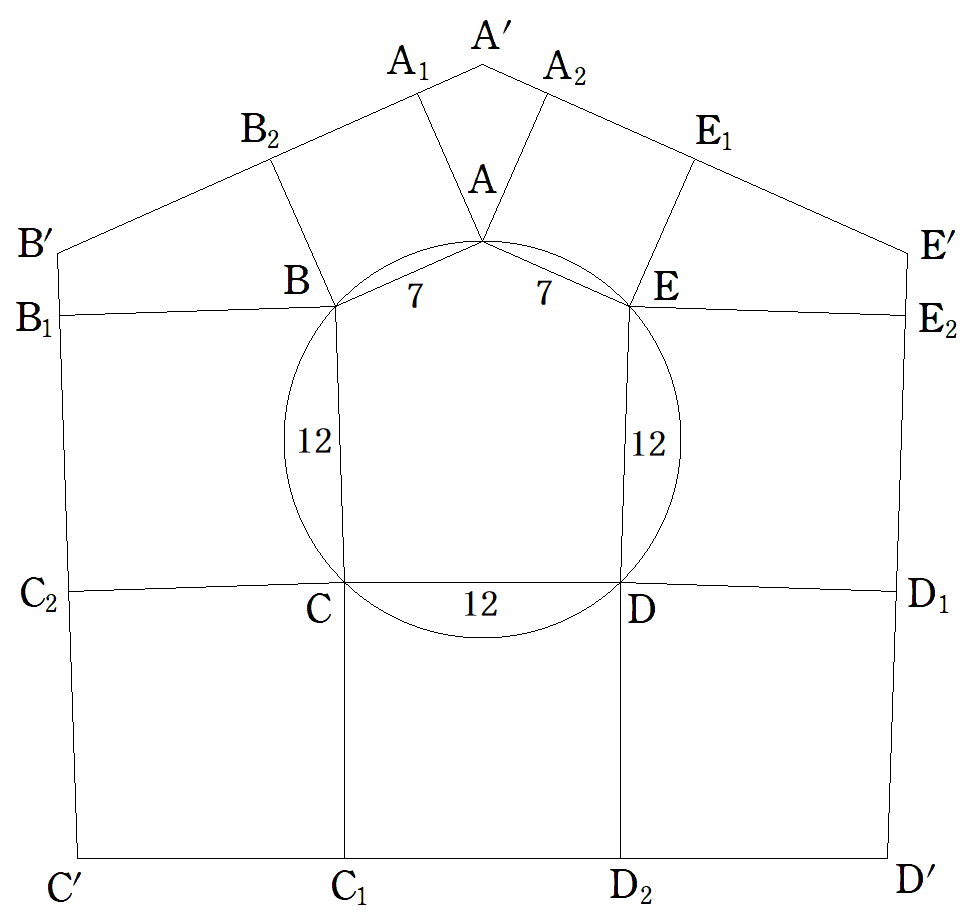

nは正の整数，α，βは鋭角とする。
tanα＝√(n+1)＋√n，tanβ＝√(n+1)－√nのとき，(α＋β)/3の値を求めよ。
△ABCの外側に正方形ADEB，BFGC，CHIAを
つくり，さらに正方形GJKH，FJLMをつくる。
BC＝5，CA＝4，AB＝6のとき，EMを求めよ。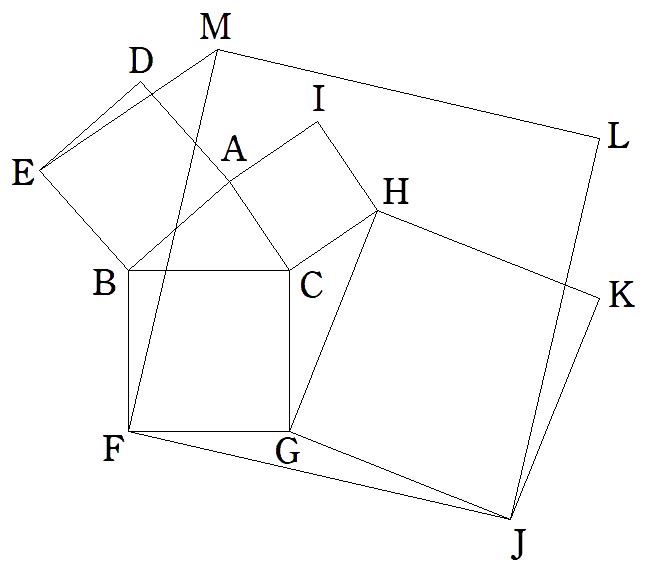
の値を求めよ。

四角形ABCDにおいて，∠ABC＝∠CDA＝90°，
AB＝a，BC＝b，CD＝c，DA＝dである。
CDの延長上に，点Eを，DE＝dとなるようにとる。
また，点Fを，図のように，FD＝c，FA＝aとなる
ようにとる。
このとき，△DEFの面積を求めよ。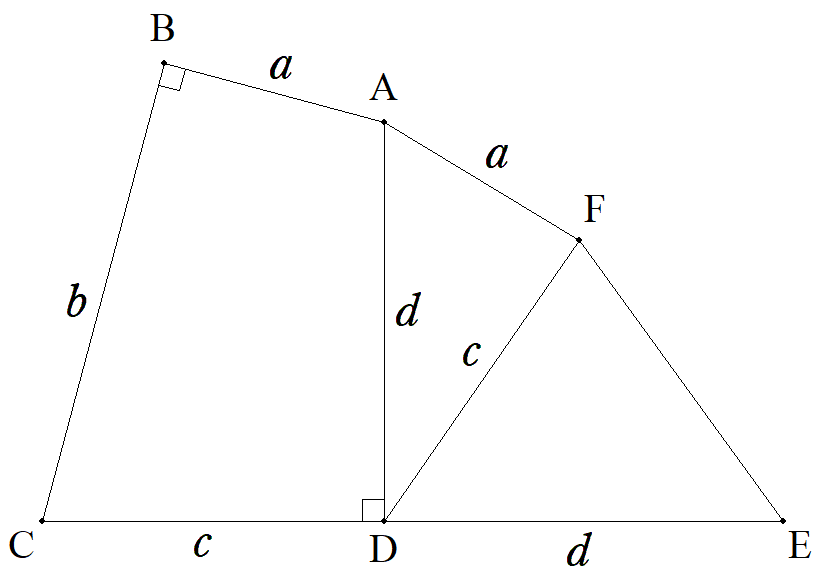

x²⁰²⁰をx⁴+x³+2x²+x+1で割ったときの余りを求めよ。
₃₈₃C₁₂₈は偶数か奇数か。
半径1，中心角90°の扇形内に，図のように，正方形赤，青が
配置されている。正方形赤，青の面積をそれぞれ求めよ。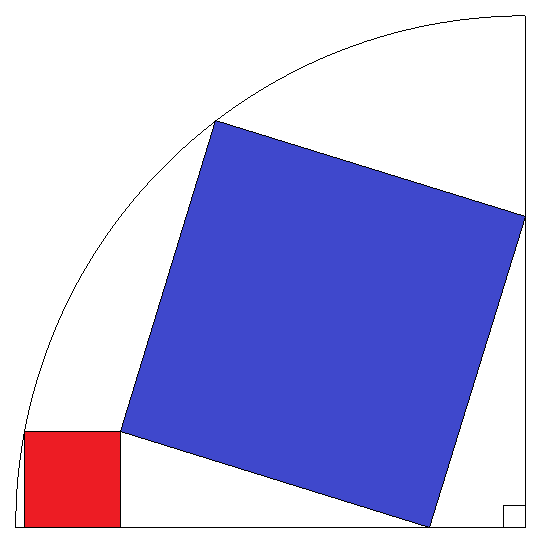
△ABCのBCの中点をD，CA上にEを，AB上にFを，
DE＝DF，∠FDE＝120°となるようにとる。
CE＝2，EA＝4，AF＝1のとき，△FBDの3辺を
それぞれ求めよ。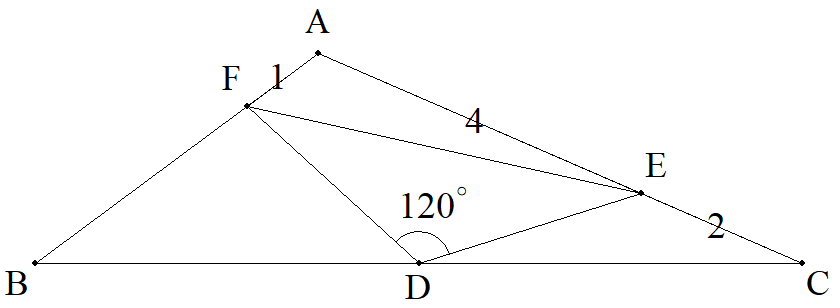
a，b，c，p，qは有理数とし，有理数の解をもたない3次方程式x³+px+q=0の1つの解をx=αとする。
aα²+bα+c=0　⇔　a=b=c=0
を示せ。

平行四辺形ABCD内に点Pを，DA上に点Qをとる。
APとBQの交点をR，DPとCQの交点をSとする。
△RAB＝15，△SCD＝20，四角形PSQR＝17のとき，
△PBCの面積を求めよ。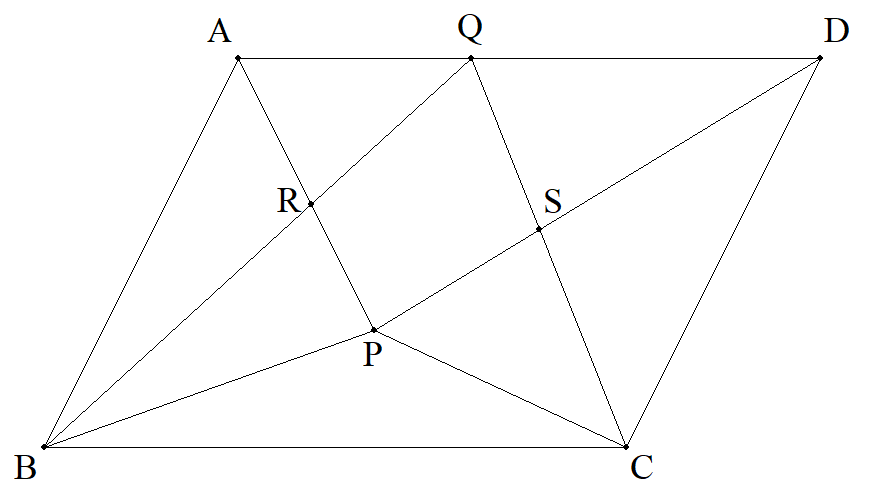

四角形ABCDについて，AC，BDの中点をそれぞれE，Fとし，
AB＝a，BC＝b，CD＝c，DA＝d，AC＝e，BD＝fのとき，
EFを求めよ。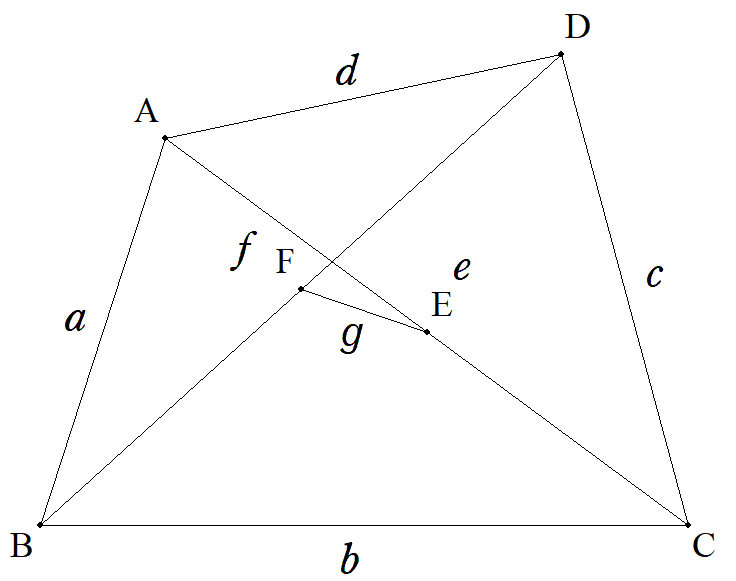
四角形ABCDについて，AC，BDの中点をそれぞれE，Fとし，
AB＝a，BC＝b，CD＝c，DA＝d，EC＝e，FB＝f，EF＝gのとき，
(a²+b²+c²+d²)/(e²+f²+g²)の値を求めよ。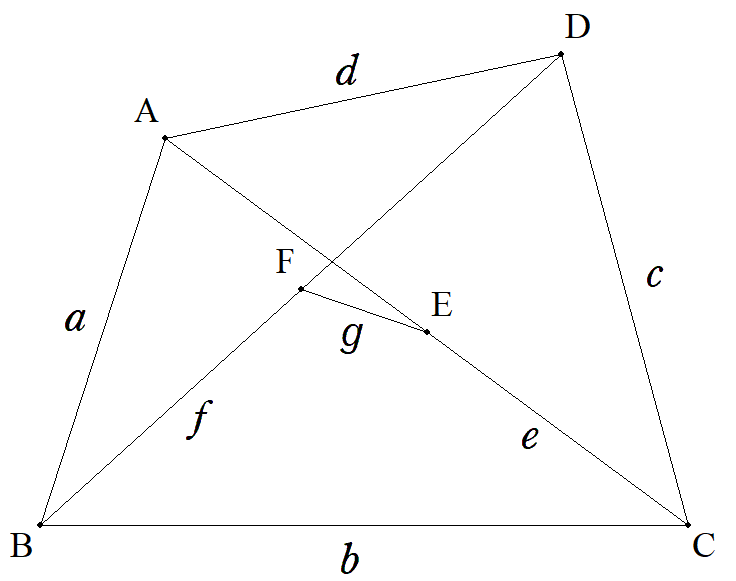
四角形ABCDについて，AB＝5，BC＝8，CD＝3，
DA＝5，∠ABC＝60°である。
AC，BDの中点をそれぞれE，Fとするとき，EFを
求めよ。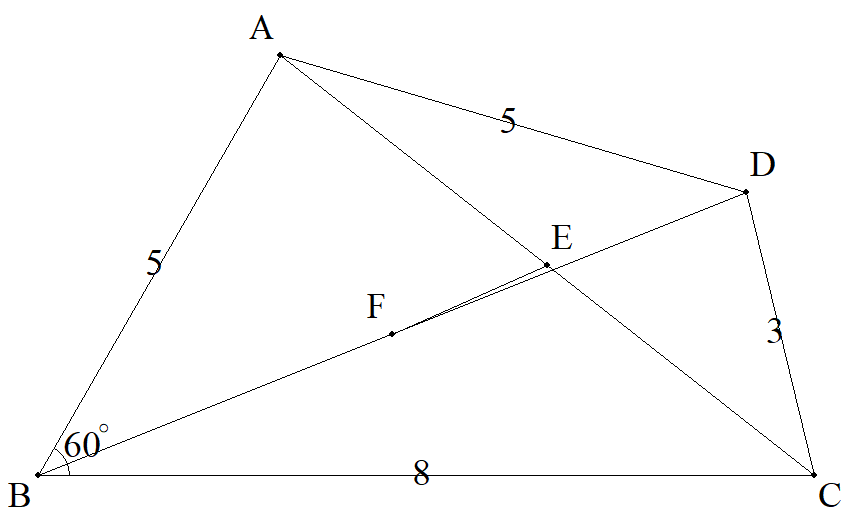

△ABCの内心をIとし，線分AI，BI，CIと内接円との交点を
それぞれD，E，Fとする。△ABC＝S，s＝(a+b+c)/2とおく
とき，△DEF/△ABCの値をa，b，c，s，Sを用いて表せ。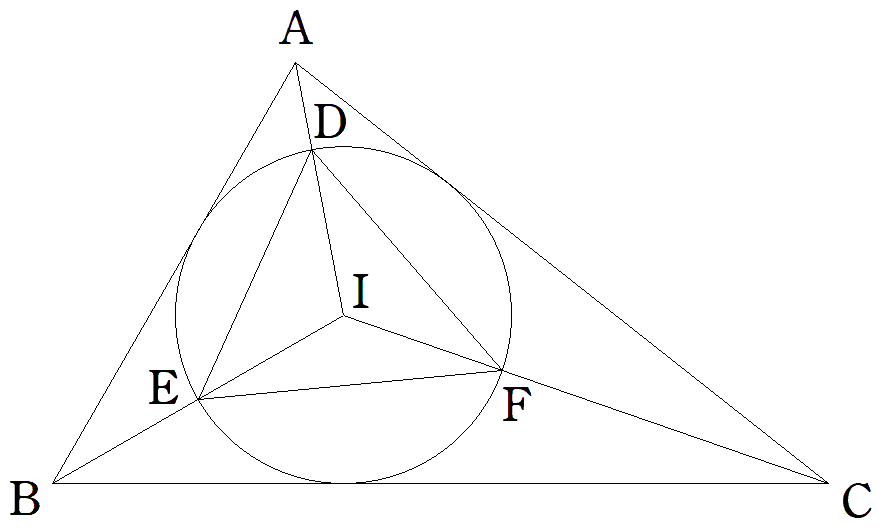

1辺1の正方形内に，図のように6個の正三角形が左右対称に
なるように配置されている。黄の正三角形の1辺を求めよ。

BC：CA：AB＝4：3：5である△ABCのBC上に点Pをとり，
PCを半径とする円とABとの交点をAに近い方からD，Eと
する。PC=13，DE＝10のとき，△ADCの面積を求めよ。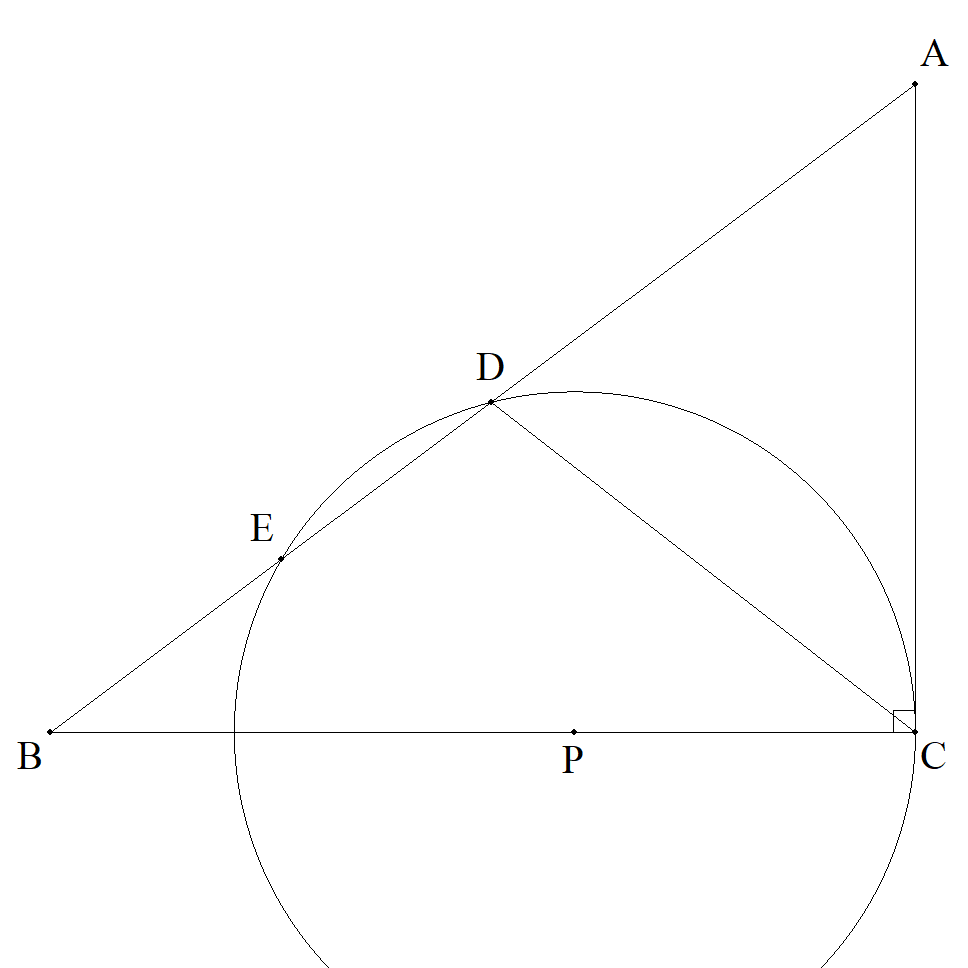

AB=1である長方形ABCDについて，
BからACに下した垂線の足をEとする。
∠DEC＝θのとき，BCをtanθを用いて表せ。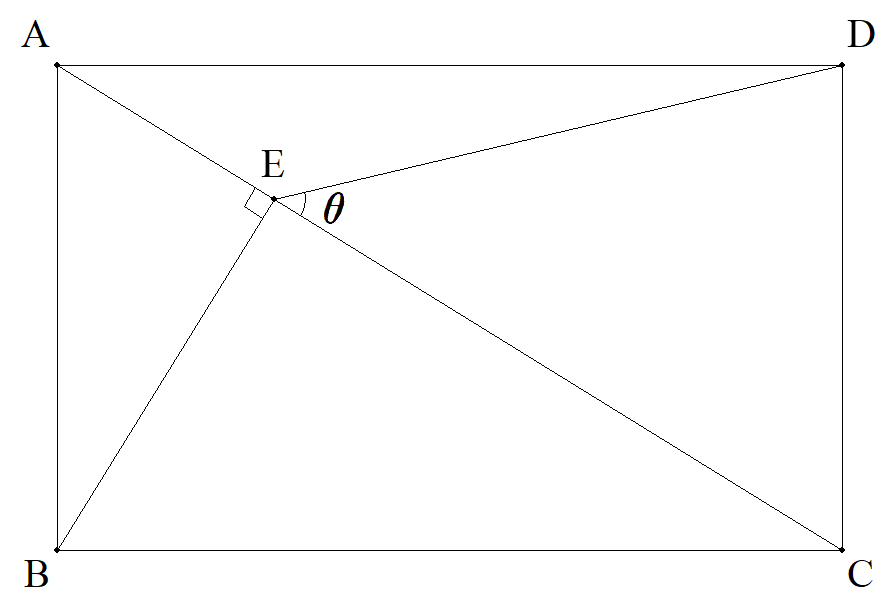

長方形ABCDの周あるいは内部に点Pをとる。
AP=a，PB=b，CP=c，DP=dのとき，
次の問いに答えよ。
(1)　a，b，c，dの関係式を求めよ。
(2)　長方形の面積の最大値を求めよ。
　　また，そのときのAB，ADの長さを求めよ。
(3)　長方形の面積の最小値を求めよ。
　　また，そのときのAB，ADの長さを求めよ。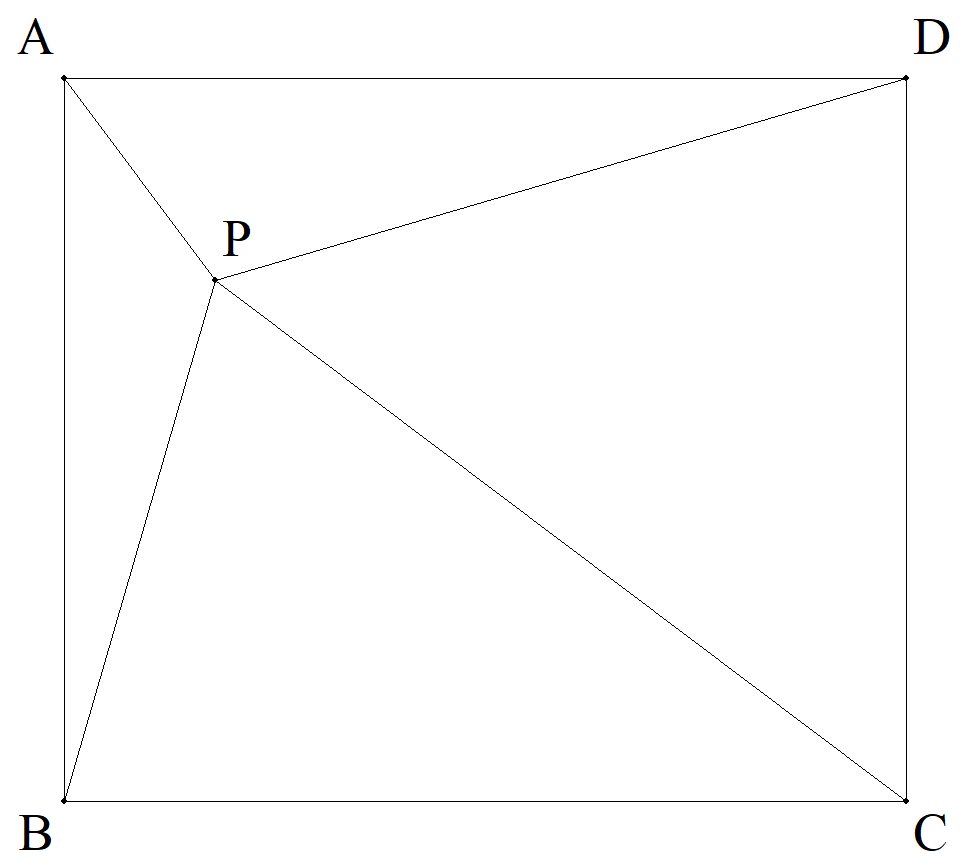

鋭角三角形ABCについて，B，CからCA，ABに
下した垂線の足をそれぞれD，E，CA，ABの
中点をそれぞれF，Gとする。
DG⊥EFのとき，∠Aを求めよ。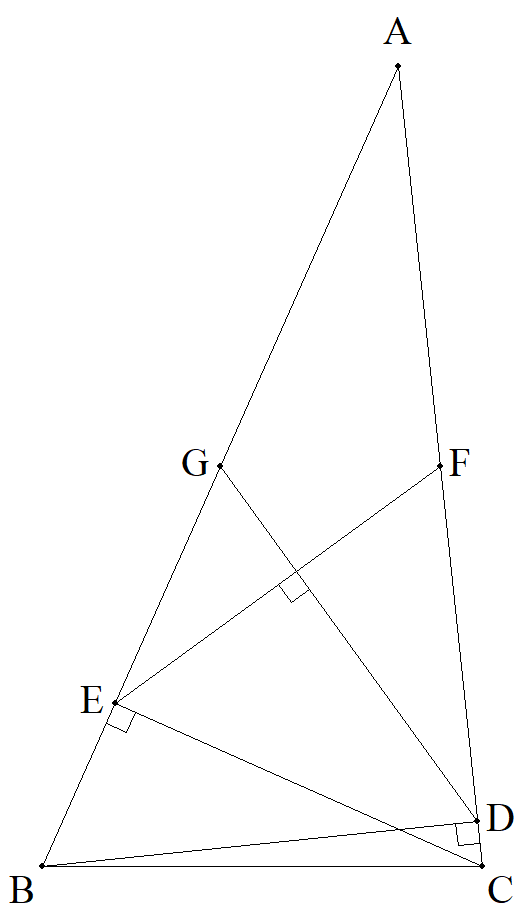
円Oに内接する正十角形ABCDEFGHIJの1辺をa，
正五角形ACEGIの1辺をbとする。
b²-a²＝2のとき，円Oの面積を求めよ。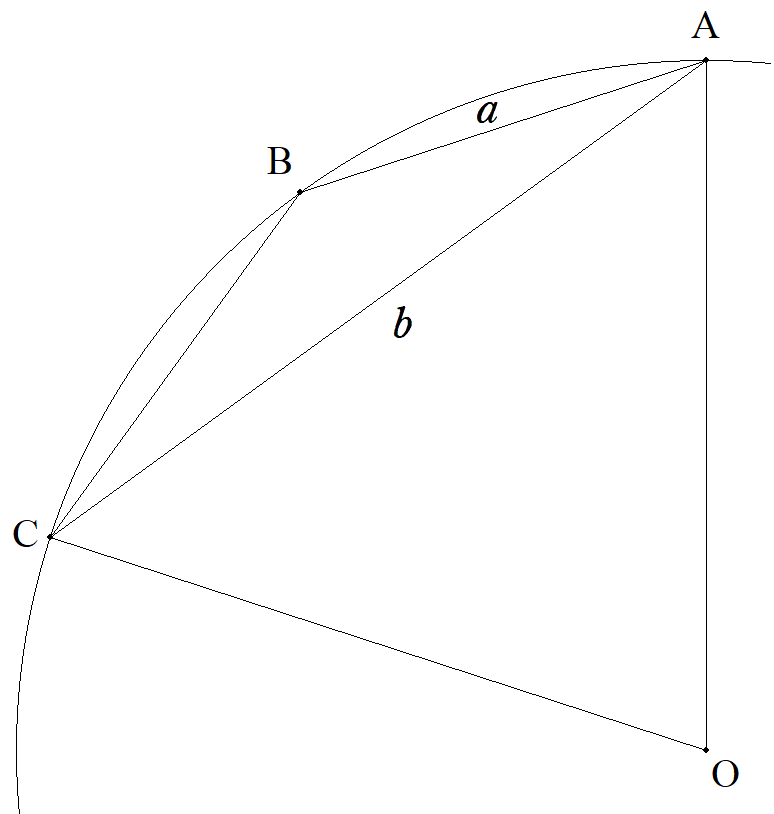

△ABCの外側に，AB，CAを1辺とする正方形ADEB，ACFGをつくる。
BFに関してAの反対側にHをとり，BFを等辺とする直角二等辺三角形
BHFをつくる。EFとAB，CAとの交点をそれぞれI，Jとする。
△AIJ＝1，△BIE＝3，△CFJ＝5のとき，△BHC－△ABCの値を求めよ。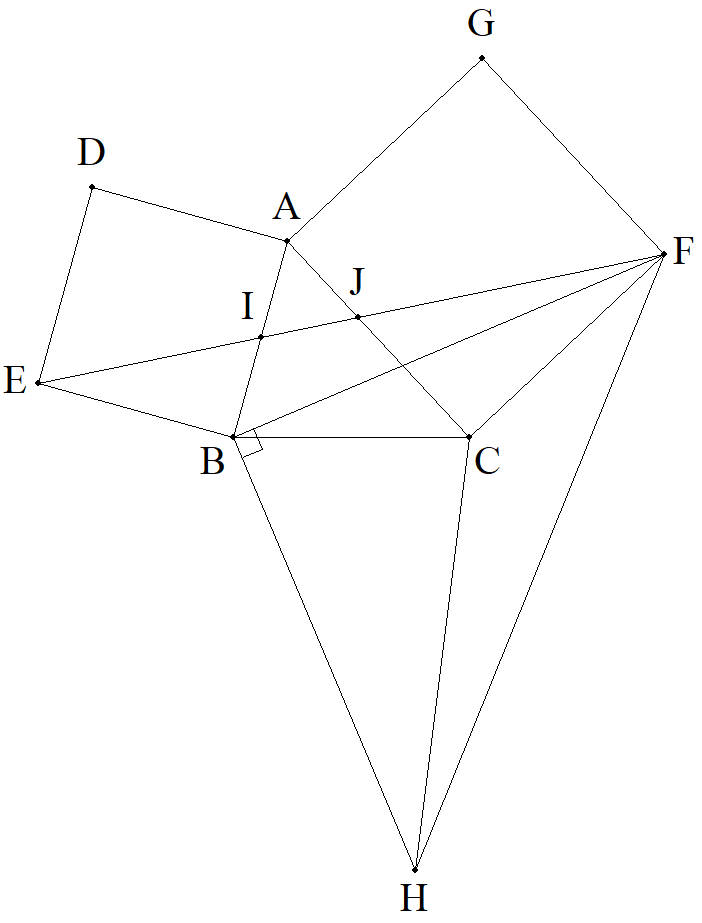

iは虚数単位とする。
3次方程式x³=1+iの解を，x=a+bi（a，bは実数）の形で求めよ。
1辺2の正三角形ABCの外側に，正方形ADEB，BFGC，CHIAをつくる。
BHとCEの交点をP，CDとAGの交点をQ，AFとBIの交点をRとする。
△PQRの面積を求めよ。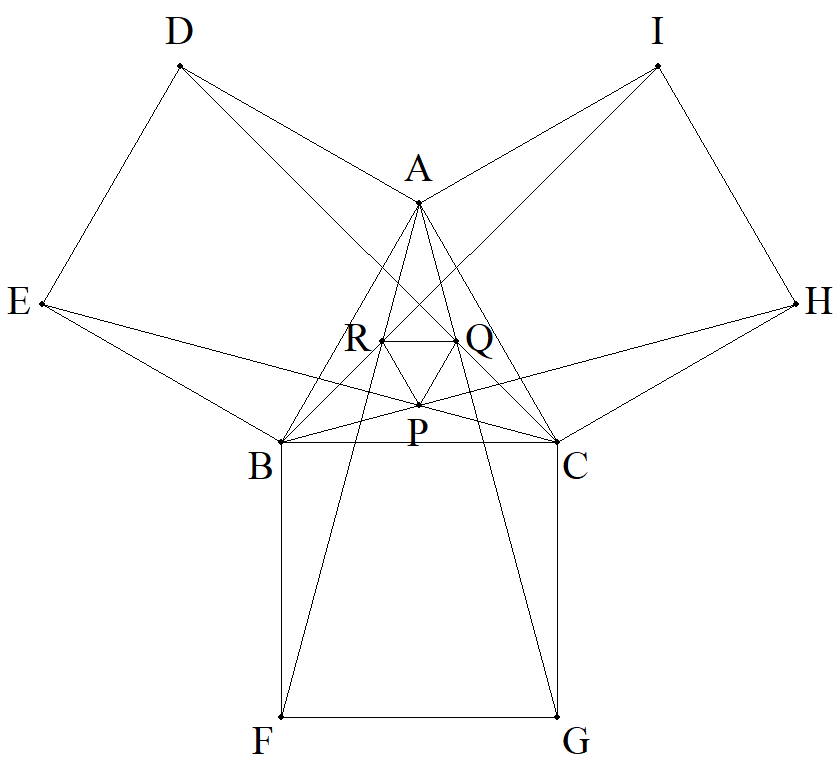

△ABCの外側に，正方形ADEB，BFGC，CHIAをつくる。
BHとCEの交点をP，CDとAGの交点をQ，AFとBIの交点をRとする。
△PQRの面積をBC＝a，CA＝b，AB＝c，△ABC＝Sを用いて表せ。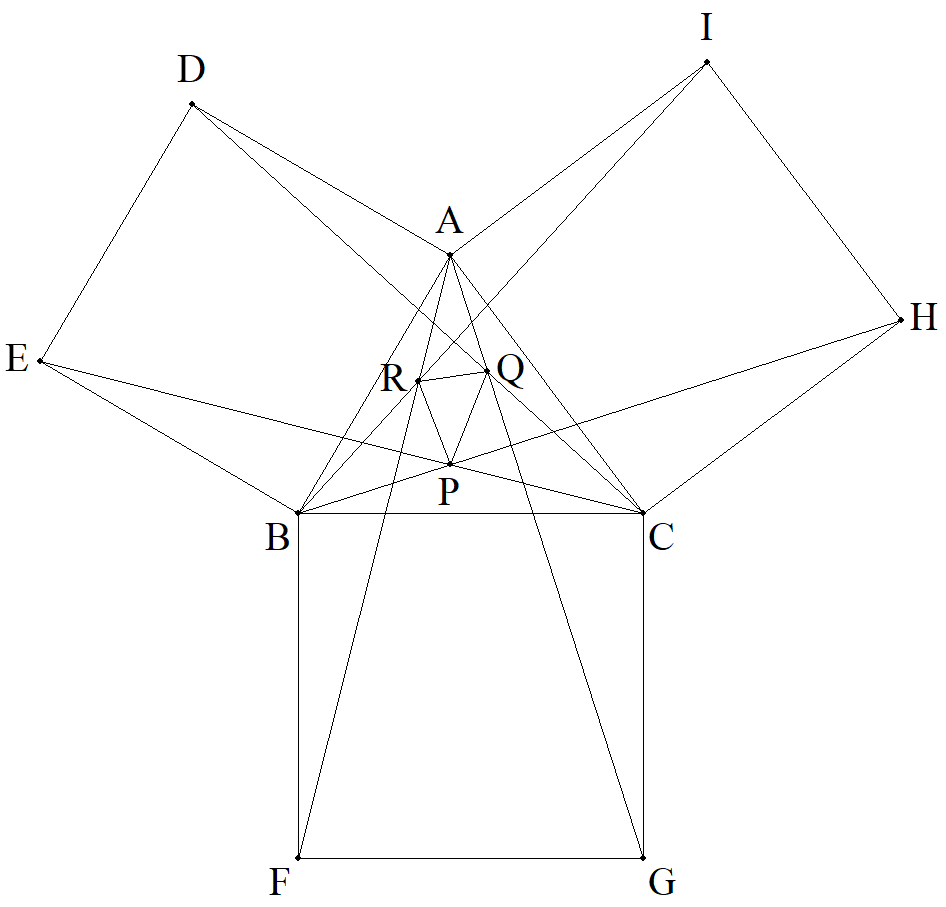

半径1の半円内に図のように甲乙丙丁戊己庚円が配置されている。
甲円の半径が1/3のとき，他の円の半径をそれぞれ求めよ。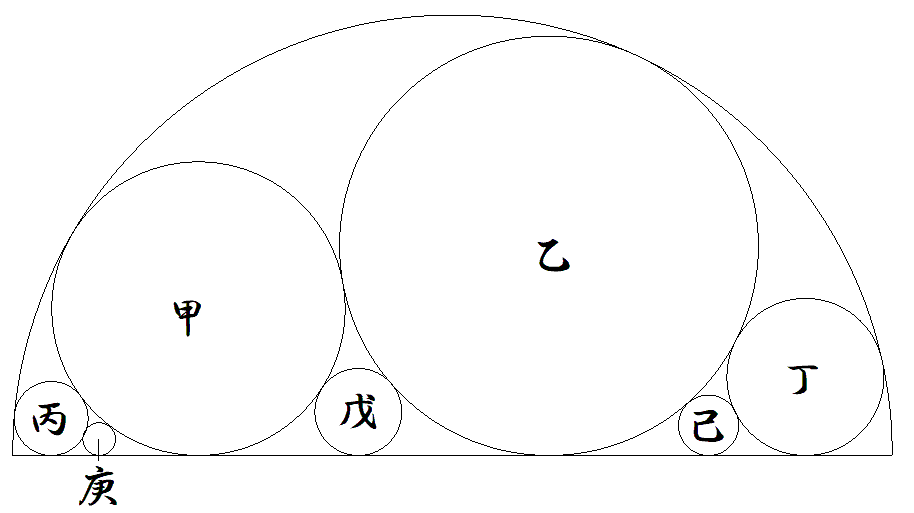
半円内に図のように甲乙丙丁戊己庚円が配置されている。
己庚円の半径がそれぞれ2，1のとき，戊円の半径を求めよ。
正三角形に図のように甲円2個，乙円4個が配置されている。
（甲径）÷（乙径）の値を求めよ。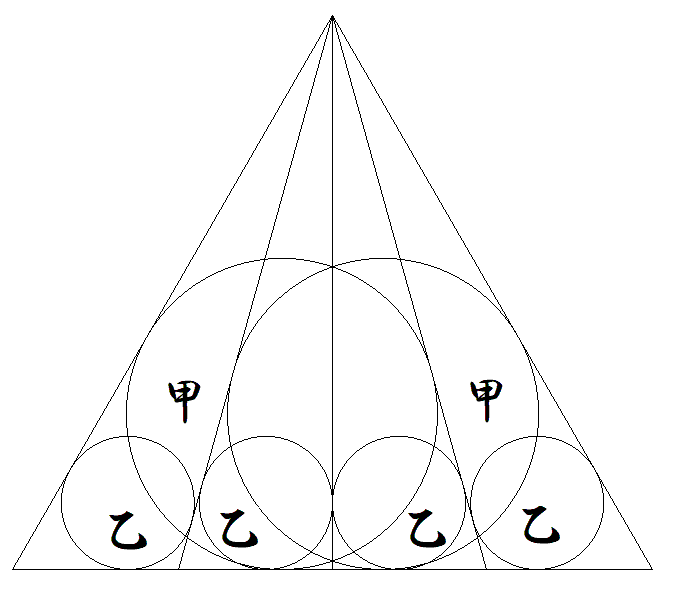
∠B＝38°，∠C＝90°である△ABCについて，
点DをAB上にAD＝BCとなるようにとり，
点EをBC上にEC＝BDとなるようにとる。
このとき，∠CAEを求めよ。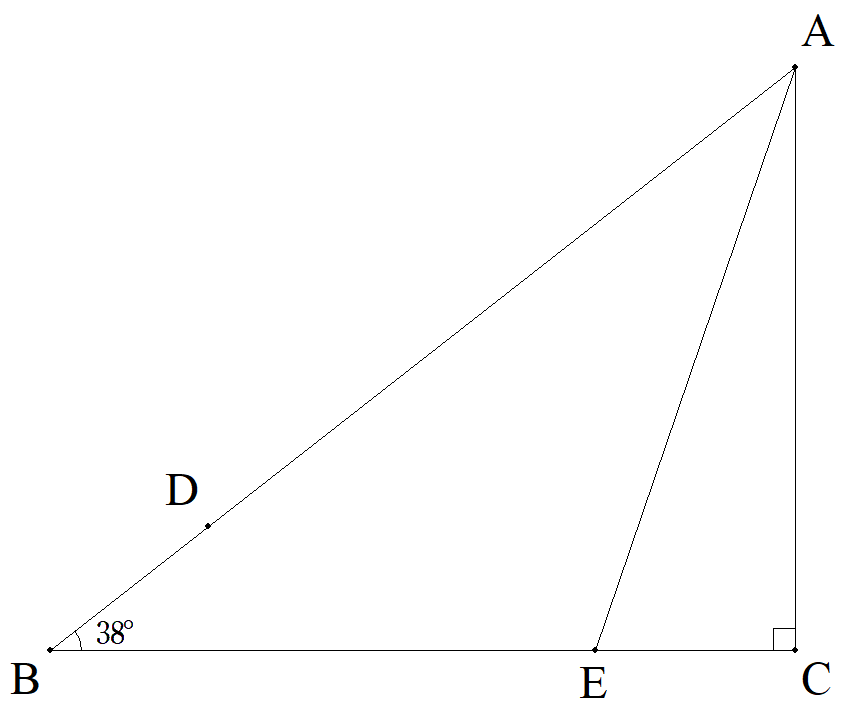
1辺2の正三角形に図のように5円甲乙丙が配置されている。
各円の半径を求めよ。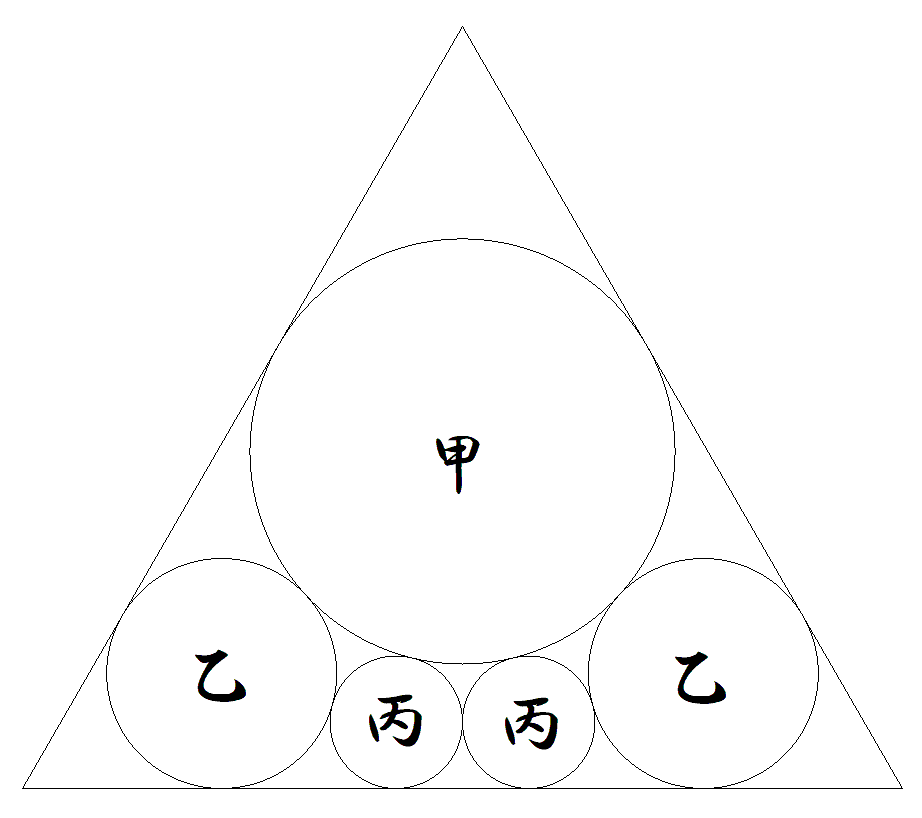
1辺2の正三角形内に図のように甲乙丙丁
10個の円が配置されている。
各円の半径を求めよ。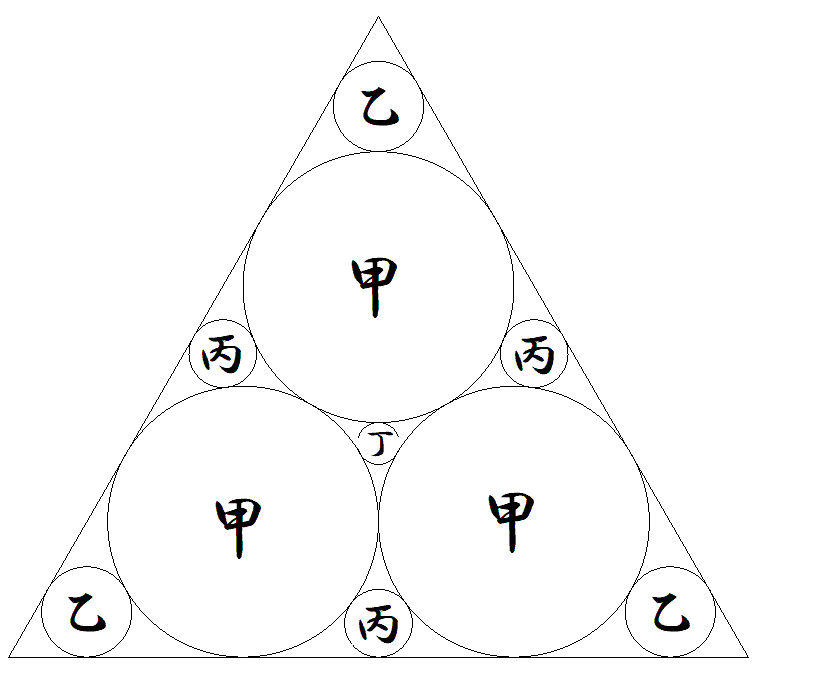
1辺4の正方形内に図のように甲円4個，丙円2個，
乙丁円が各1個が配置されている。
各円の半径を求めよ。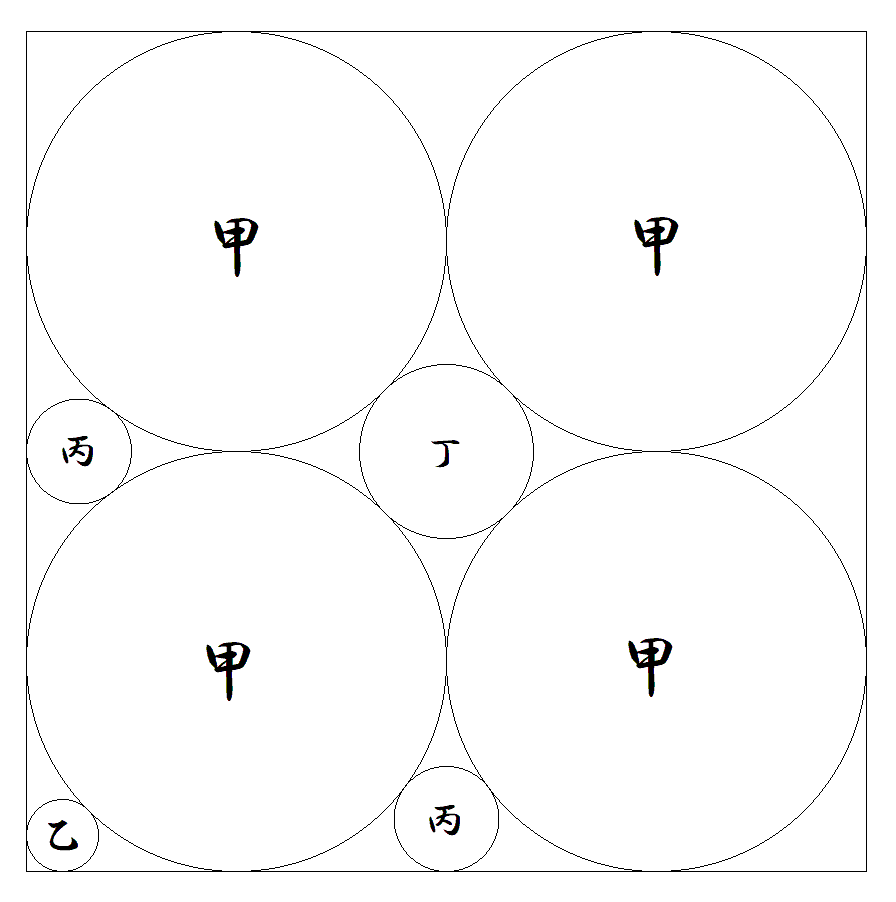
1辺1の正5角形内に図のように甲円5個，
乙丙丁円が各1個が配置されている。
各円の半径を求めよ。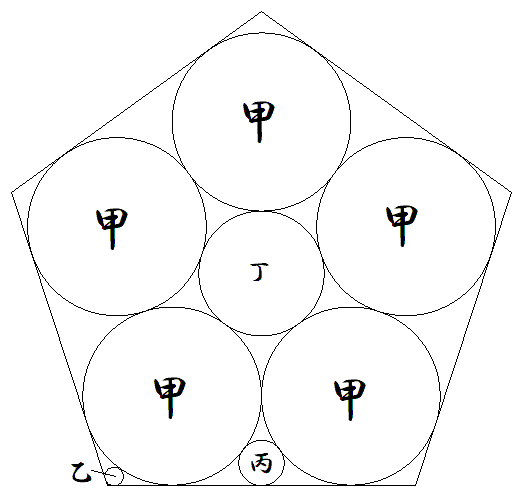

1辺aの正n角形内に図のように甲円n個，
乙丙丁円が各1個が配置されている。
（図はn＝5の場合）
(1)　甲円の半径をaを用いて表せ。
(2)　甲円の半径をrとして，乙丙丁円の
　　半径をそれぞれrを用いて表せ。

右図で乙丙円の直径は長方形の辺上にある。
（戊円の半径）÷（丁円の半径）の値を求めよ。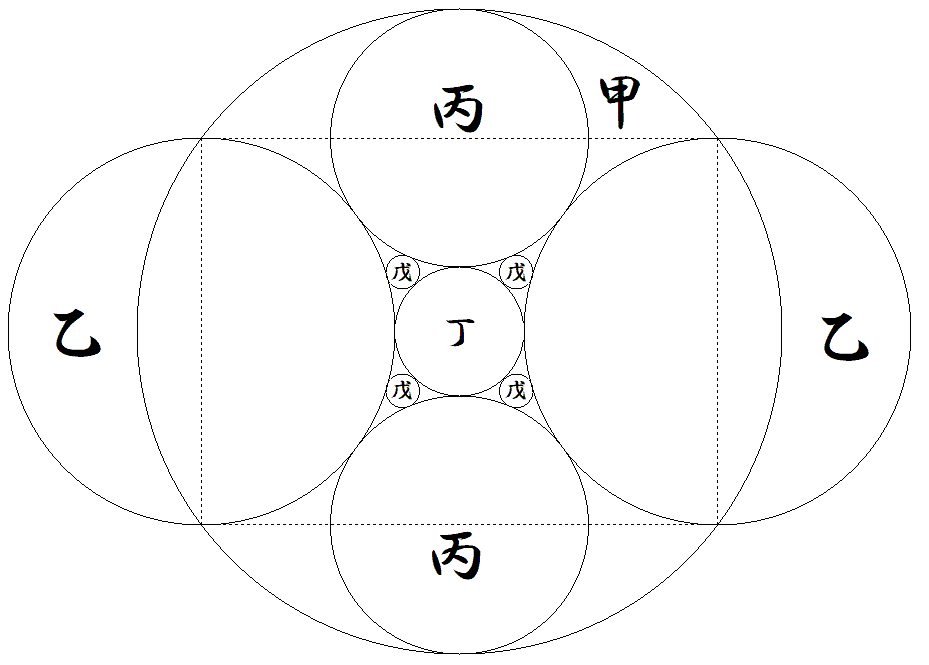

右図で二等辺三角形に甲乙丙円が接している。
(1)　（乙円の半径）÷（甲円の半径）の値を求めよ。
(2)　（丙円の半径）÷（甲円の半径）の値を求めよ。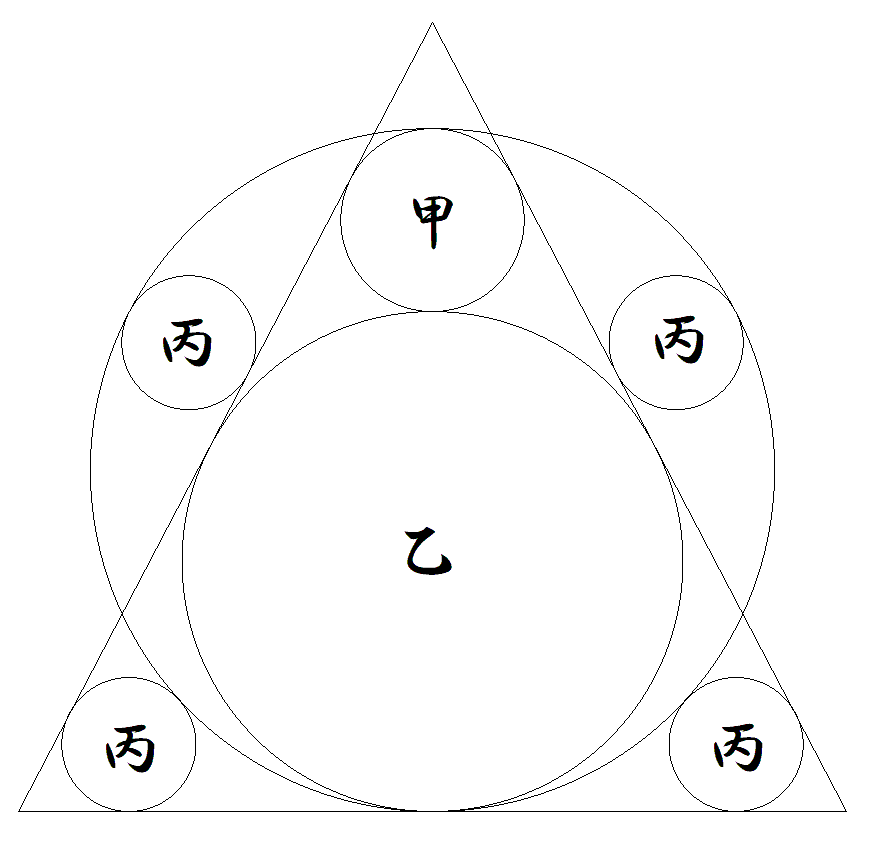

右図で3個の甲円の中心が正三角形の頂点になっている。
（乙円の半径）÷（丁円の半径）の値を求めよ。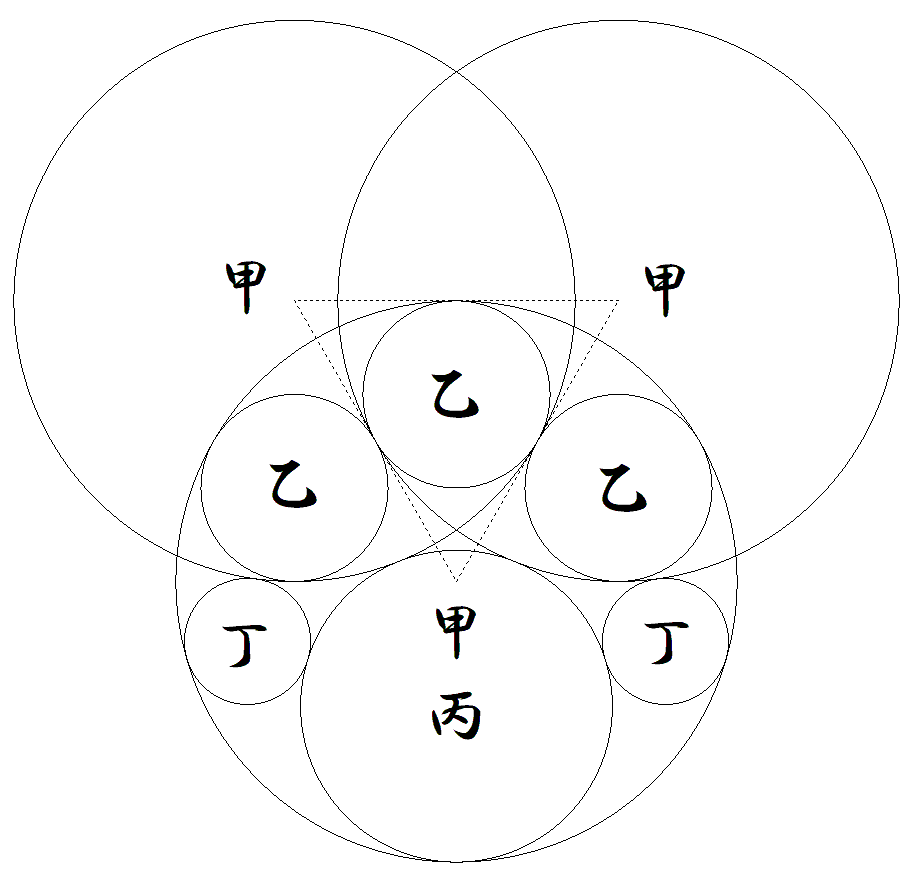
縦が5の長方形内に図のように甲乙丙丁円が配置されている。
長方形の横を求めよ。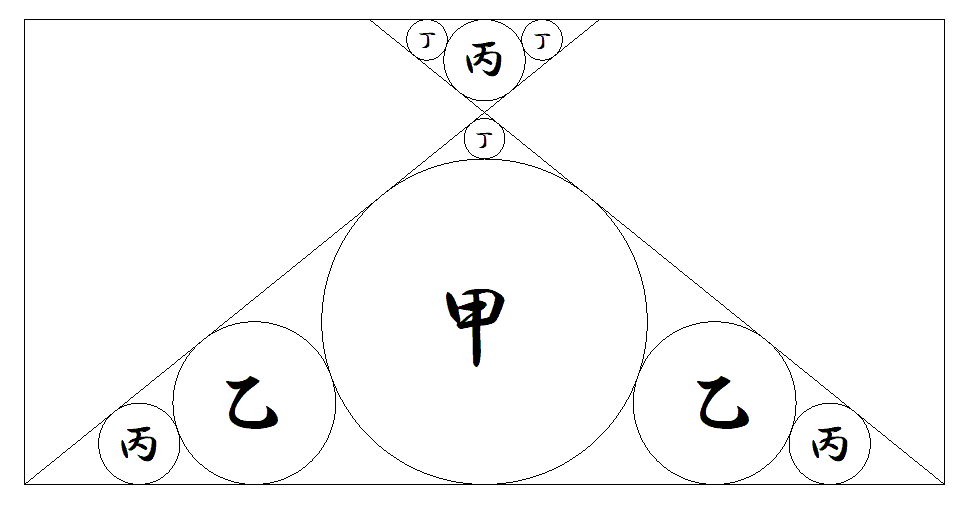
甲円3個，乙円2個が図のように配置されている。
甲円の半径が1のとき，乙円の半径を求めよ。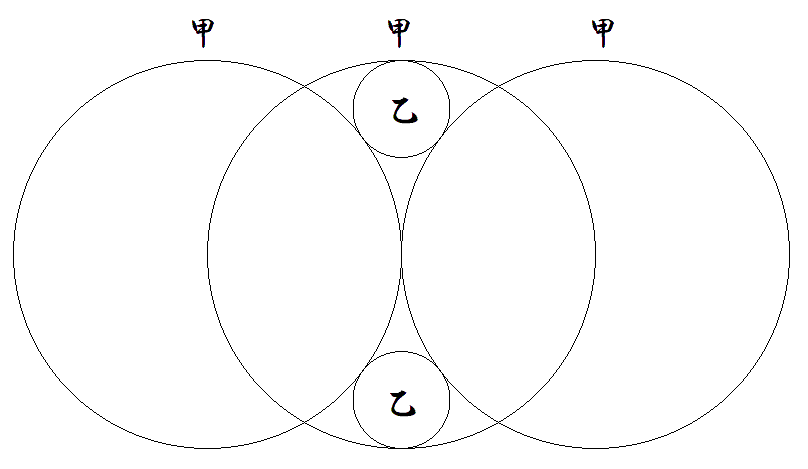

1辺の長さが1である正方形内に，向かい合う辺
を1辺とする正三角形を2個つくり，図のように，
甲円1個と乙円2個を内接させる。
このとき，甲乙円の半径をそれぞれ求めよ。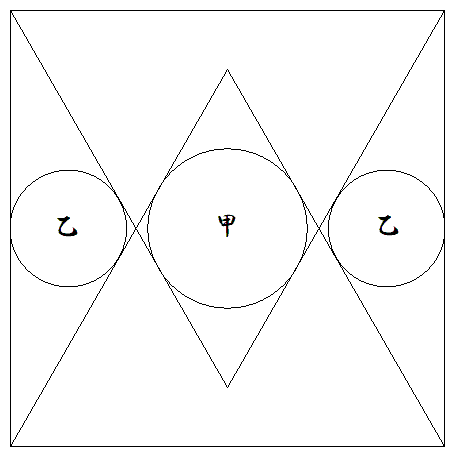

横の長さが1である長方形の向かい合う
横の辺を1辺とする正三角形を2個つく
り，図のように3個の甲円を内接させる。
このとき，長方形の縦の長さと甲円の
半径をそれぞれ求めよ。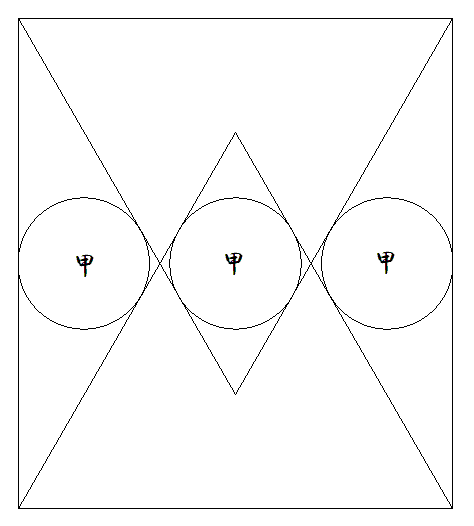

1辺の長さが1である正方形内に，向かい合う
辺を1辺とする二等辺三角形を2個つくり，図
のように，3個の甲円を内接させる。このとき，
二等辺三角形の等辺と甲円の半径をそれぞれ
求めよ。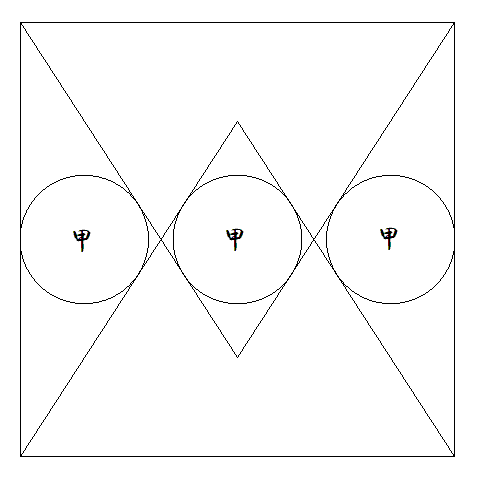

縦a，横bである長方形内に横を底辺とする
向かい合う二等辺三角形を2個つくり，図の
ように3個の甲円を内接させる。二等辺三角形
の等辺をcとするとき，aをb，cを用いて表せ。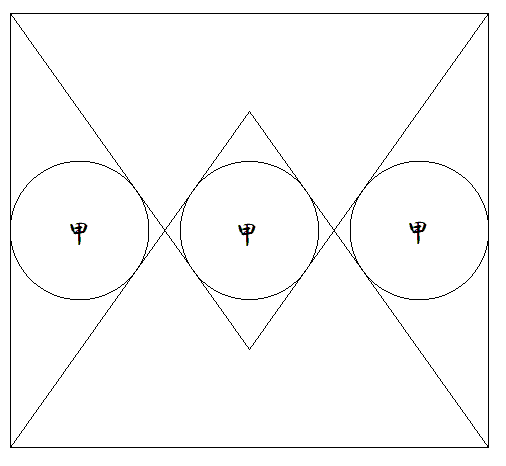

長方形の中に4本の等しい斜線を引き，
甲円1個，乙円4個を入れる。長方形の
縦を1，横をxとするとき，xの満たす
方程式を求めよ。（根号を含まない形で）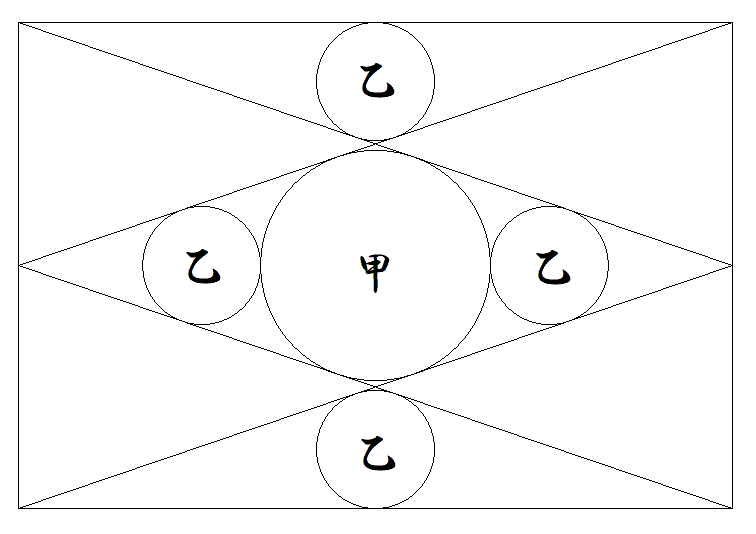

1辺の長さが1である正方形内に
4本の長さが等しい斜線を引き，
図のように甲円5個，乙円2個を
入れる。このとき斜線の長さx
の満たす方程式を求めよ。（根号
を含まない形で）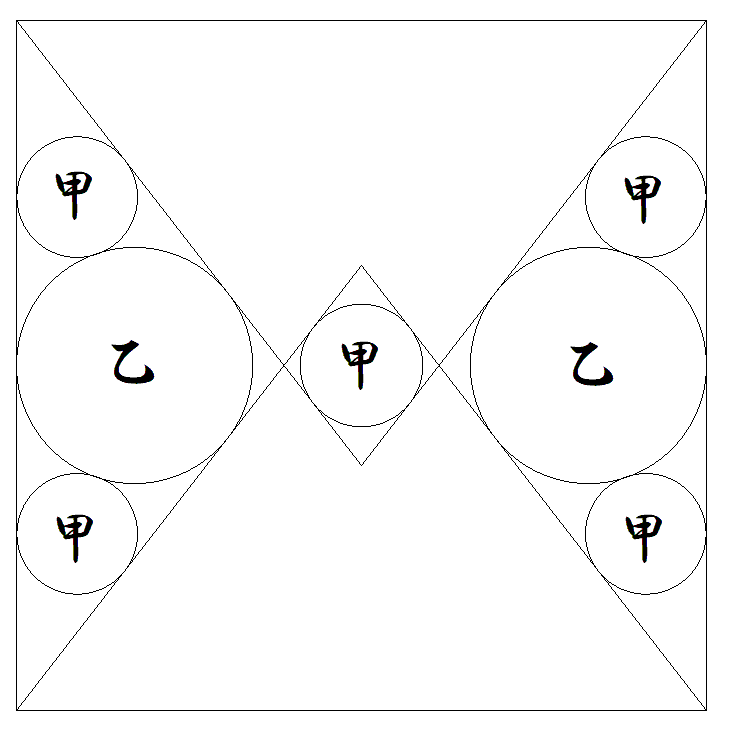

1辺の長さが1である正方形内に
4本の等しい斜線を引き，図のよ
うに5個の甲円を入れる。
このとき，斜線の長さを求めよ。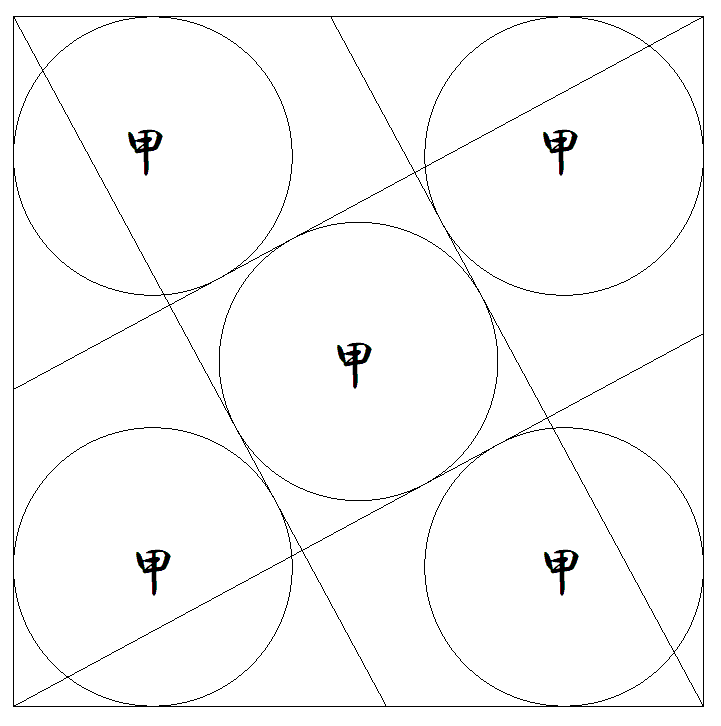
1辺の長さが1である正三角形内に
3本の等しい斜線を引き，図のよう
に4個の甲円を入れる。
このとき，斜線の長さを求めよ。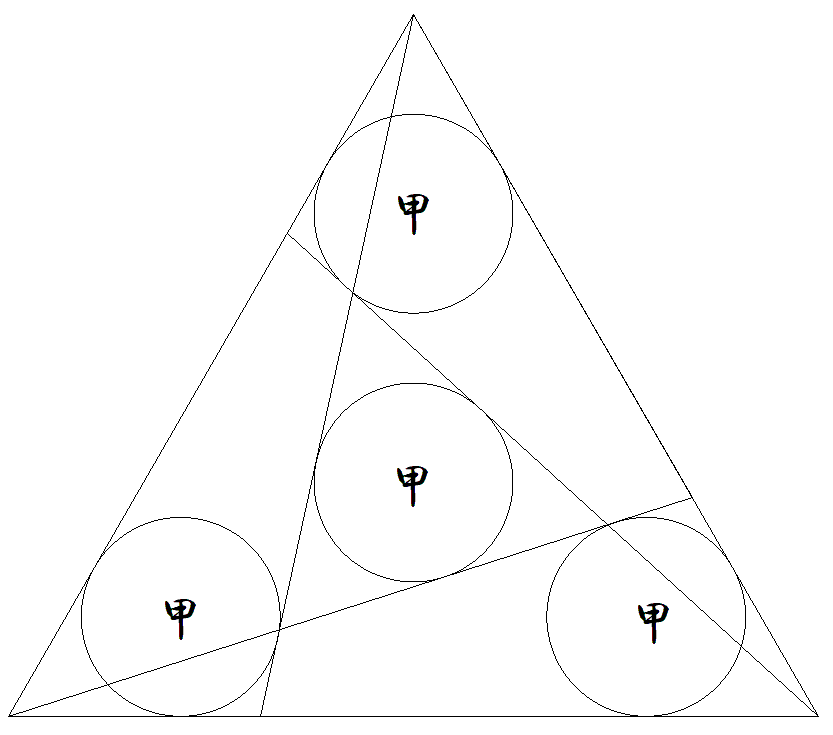

1辺の長さが1である正五角形内に図のように6個の甲円を配置する。
(1)　甲円の半径を求めよ。
(2)　五角形の対角線は中央の甲円に接するかどうか調べよ。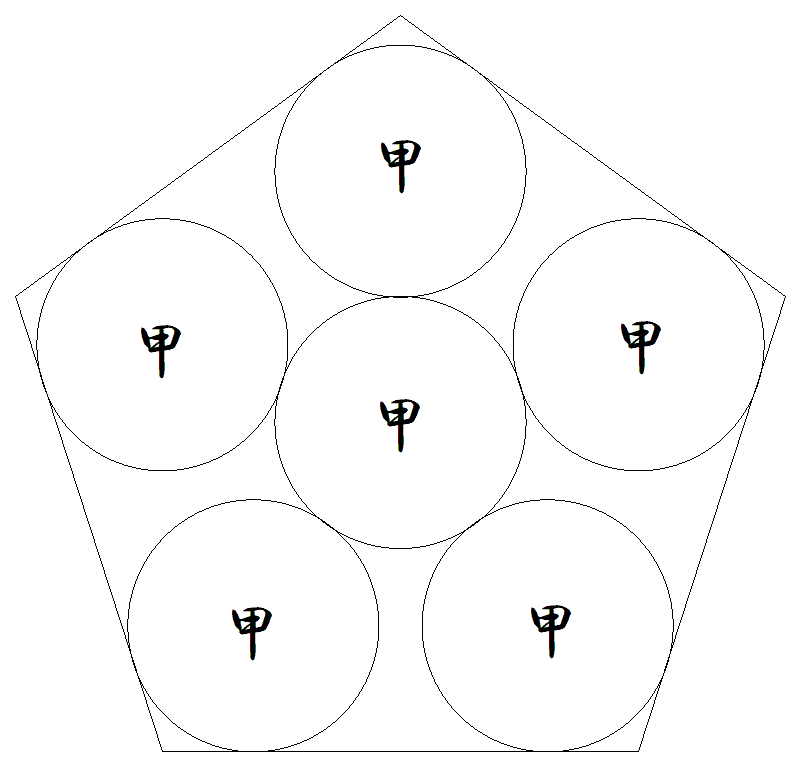