■趣味の数学問題集・Ａ問題

  1. 1辺の長さが1である正六角形内に，図のように頂点から
    等しい斜線を6本引き，甲円1個と乙円6個を入れる。
    甲，乙円の半径をそれぞれr1，r2とおくとき，r2をr1で表せ。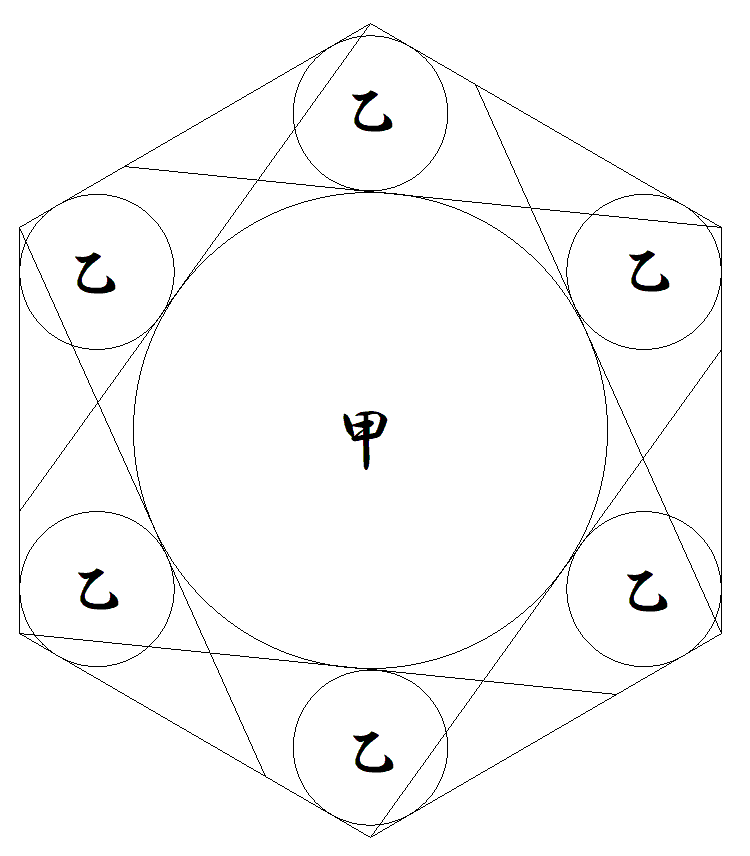






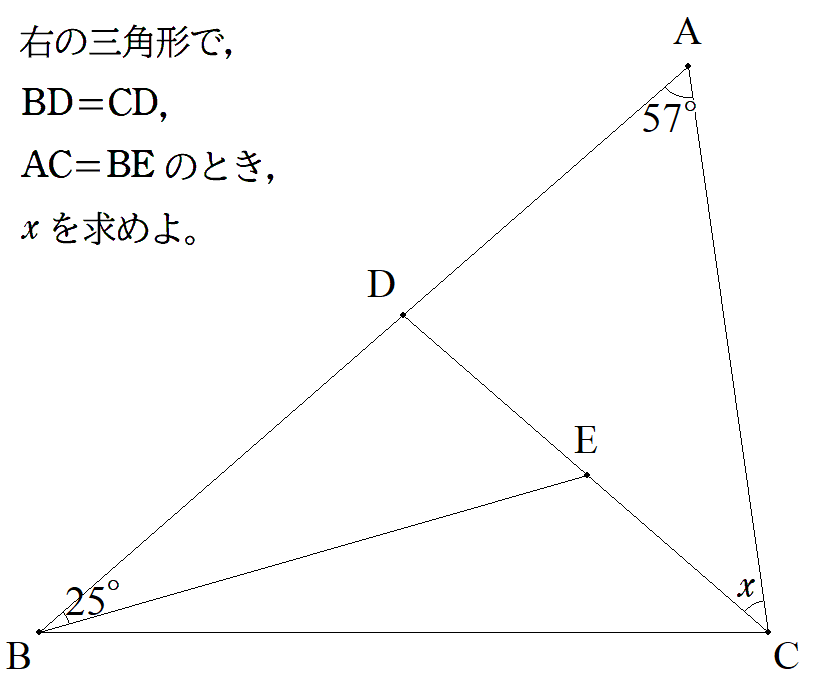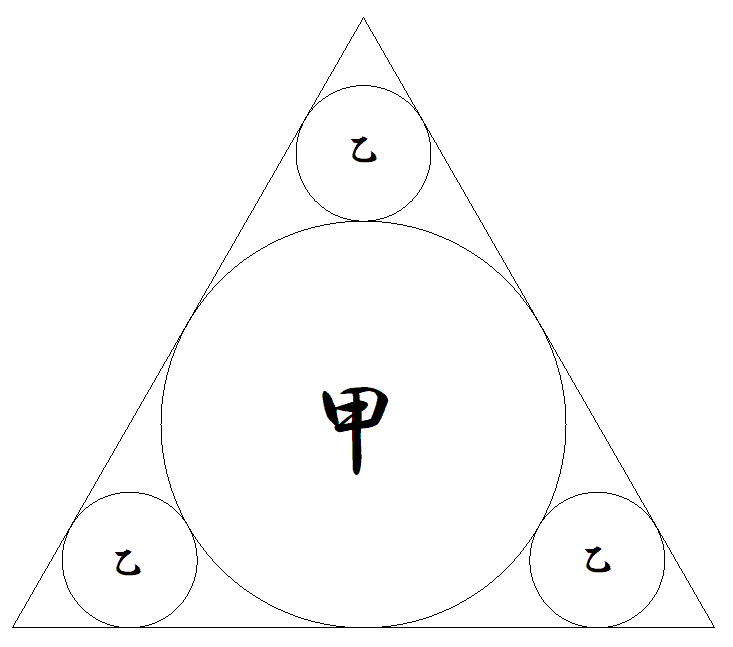
  3. 正三角形内に，図のように甲乙丙円が
    配置されている。
    甲乙丙円の半径の比を求めよ。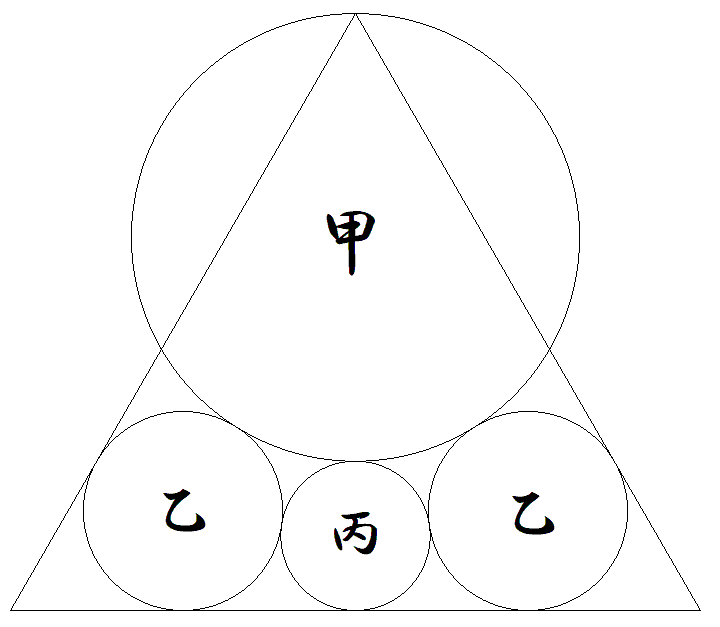



  4. 1辺の長さが2である正三角形内に，図のように
    甲乙丙丁円が配置されている。
    甲乙丙丁円の半径をそれぞれ求めよ。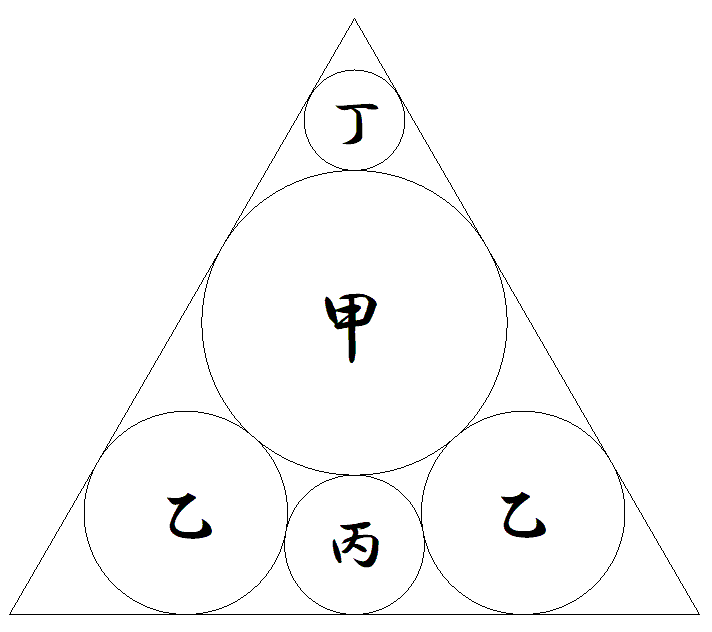



  5. 縦の長さが1である長方形内に，図のように
    甲乙丙円が配置されている。
    このとき，長方形の横の長さと，甲乙丙円
    の半径をそれぞれ求めよ。



  6. 縦の長さが1である長方形内に，図のように
    甲乙丙円が配置されている。
    このとき，長方形の横の長さと，甲乙丙円
    の半径をそれぞれ求めよ。



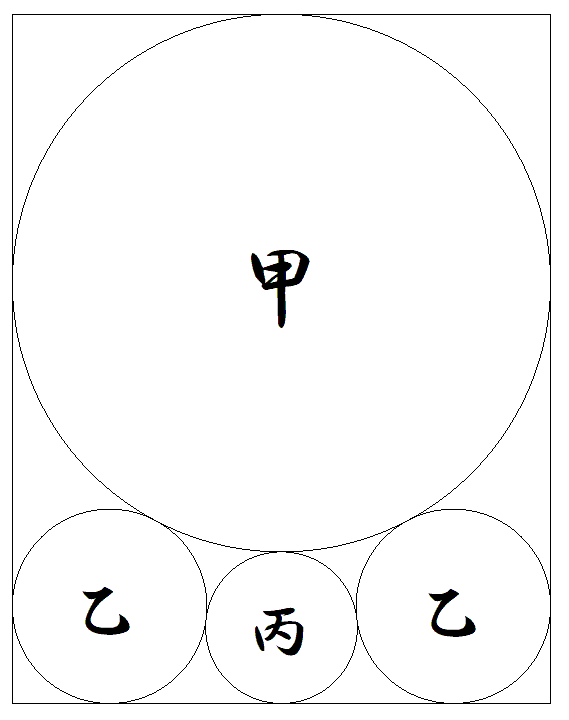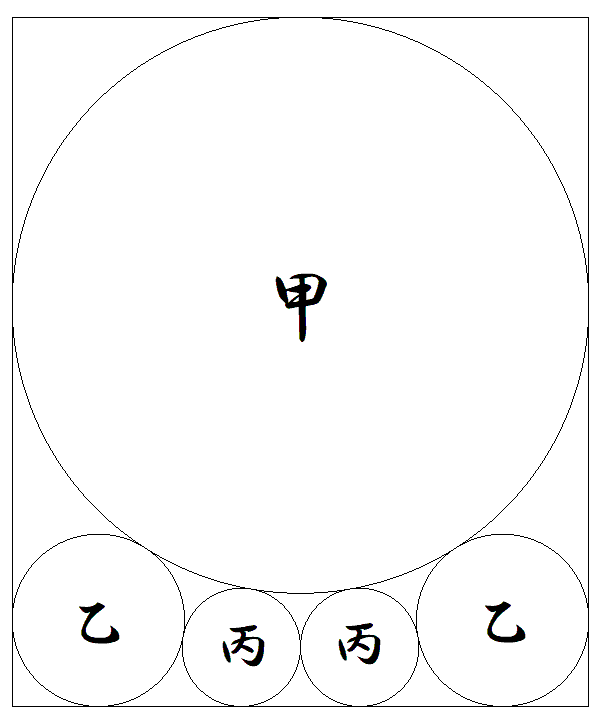  7. 縦の長さが1である長方形内に，図のように
    甲乙丙丁円が配置されている。
    長方形の横の長さxの満たす方程式を求めよ。
    ただし，方程式には根号は含まないものとする。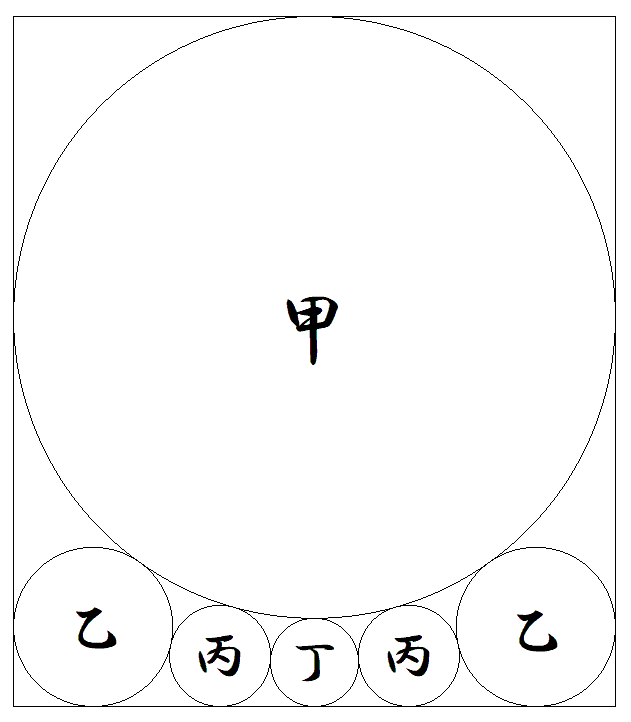



  8. 縦横の長さがそれぞれa，bである長方形内に，
    図のように2本の斜線を引き，甲乙丙丁円を配置
    する。それぞれの半径を求めよ。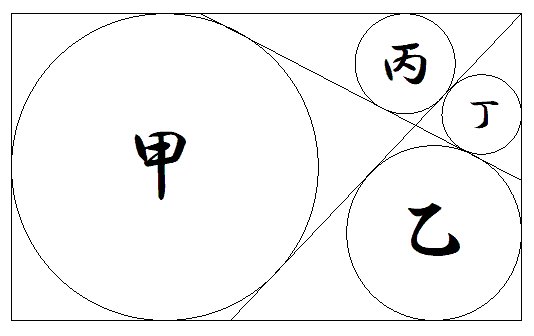



  9. 縦横の長さがそれぞれx，1である長方形内に，
    図のように2本の斜線を引き，甲乙丙円を配置
    する。甲丙円の半径の積が乙円の半径の2乗に
    等しくなるとき，xを求めよ。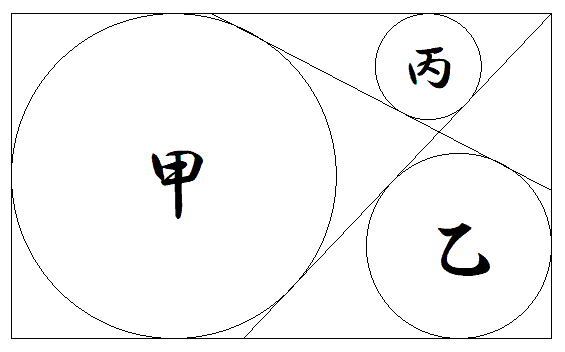



  10. 縦横の長さがそれぞれ1，xである長方形内に，
    図のように甲乙丙円が配置されている。
    このとき，xの値を求めよ。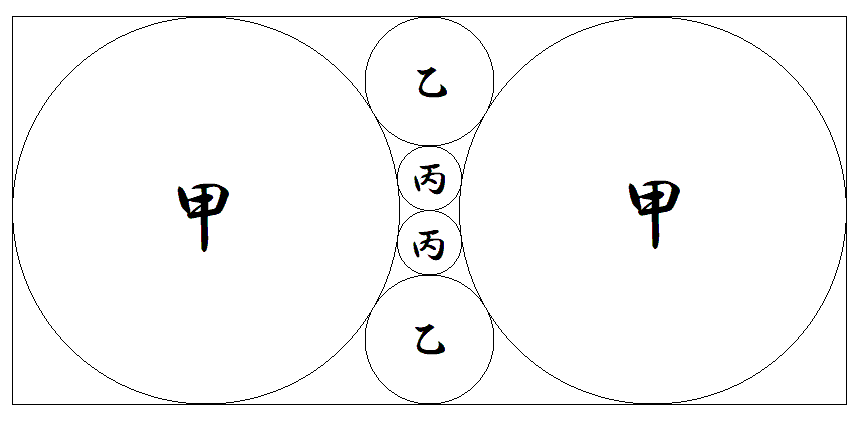



  11. △ABCについて，BC上に点Dをとる。
    BD＝a1，DC=a2（a1+a2＝a），CA＝b，
    AB＝c，△ABC＝Sとおくとき，点Aを通り，
    DにおいてBCに接する円の半径を求めよ。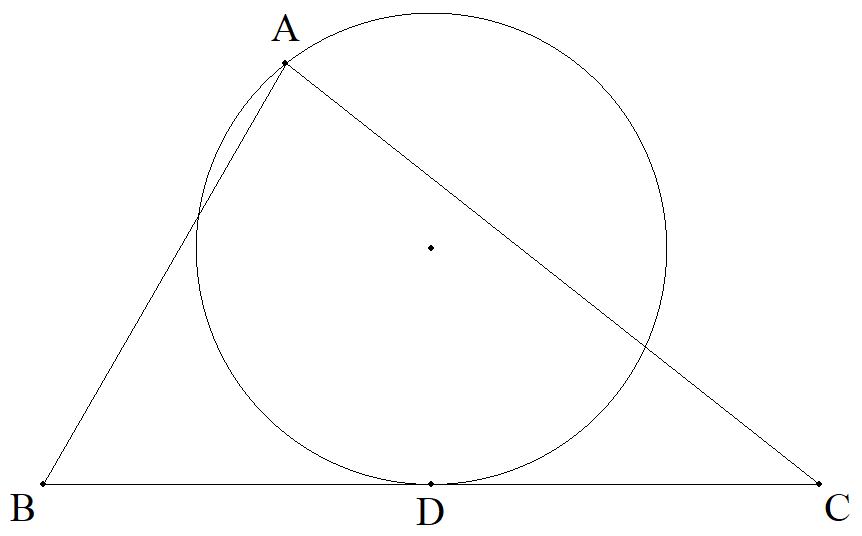



  12. △ABCについて，直線BC上の次の点Dについて，
    点DにおいてBCに接し，点Aを通る円の半径を，
    BC＝a，CA＝b，AB＝c，s＝(a+b+c)/2，
    S＝△ABC等を用いてそれぞれ求めよ。
    (1)　AからBCに下した垂線の足をD
    (2)　BCの中点をD
    (3)　∠Aの二等分線とBCとの交点をD
    (4)　△ABCの内接円とBCとの接点をD
    (5)　△ABCの∠A内の傍接円とBCとの接点をD
    (6)　△ABCの外心をOとする。AOとBCとの交点をD
    (7)　BCに関して点Aの反対側に点A´を△A´BCが正三角形
    　　になるようにとる。AA´とBCとの交点をD
    (8)　△ABC内に点Pを∠PAB＝∠PBC＝∠PCAとなるようにとり，
    　　APとBCとの交点をD
    (9)　△ABCの頂点AからBCに下ろした垂線の足をEとする。AEを
    　　∠Aの二等分線で対称に折り返した直線とBCとの交点をD



  13. 円に内接する正三角形△ABCについて，
    AB，ACの中点をそれぞれD，Eとし，
    図のように，DEと円の交点をFとする。
    ACに関してBの反対側に点Gを，AG＝AE，
    EG＝EFとなるようにとる。
    このとき，∠EAGの大きさを求めよ。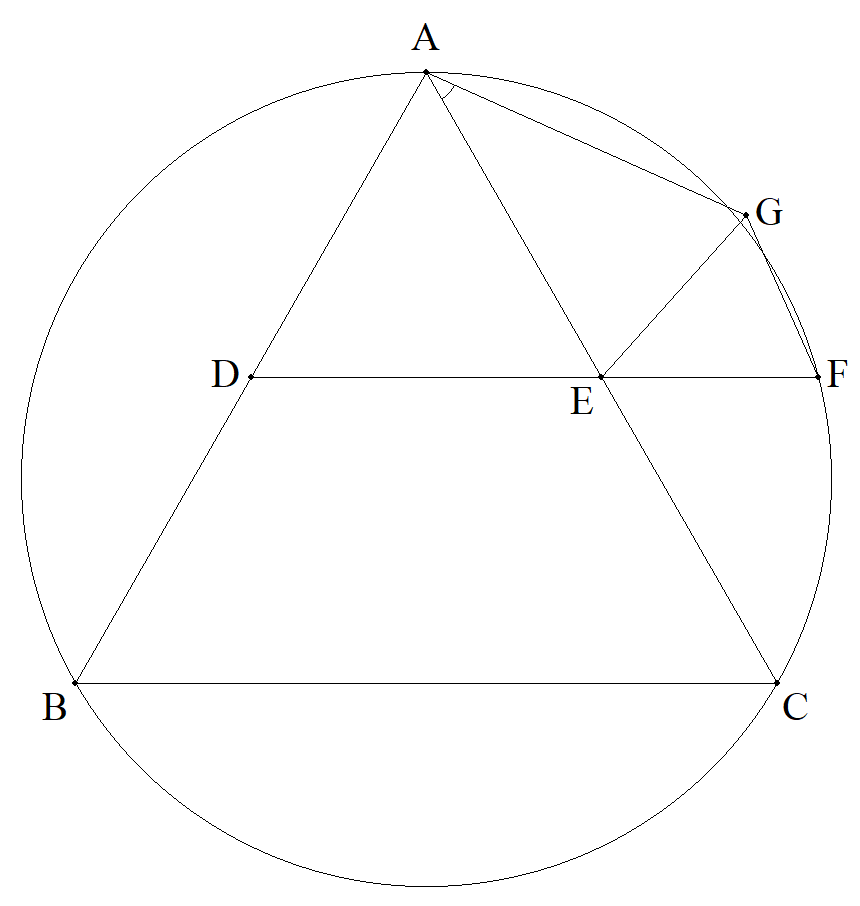



  14. 五角形ABCDEの重心をGとする。
    EA＝AB＝a，BC＝DE=b，CD=c，
    ∠BCD＝∠CDE＝90°のとき，AGを求めよ。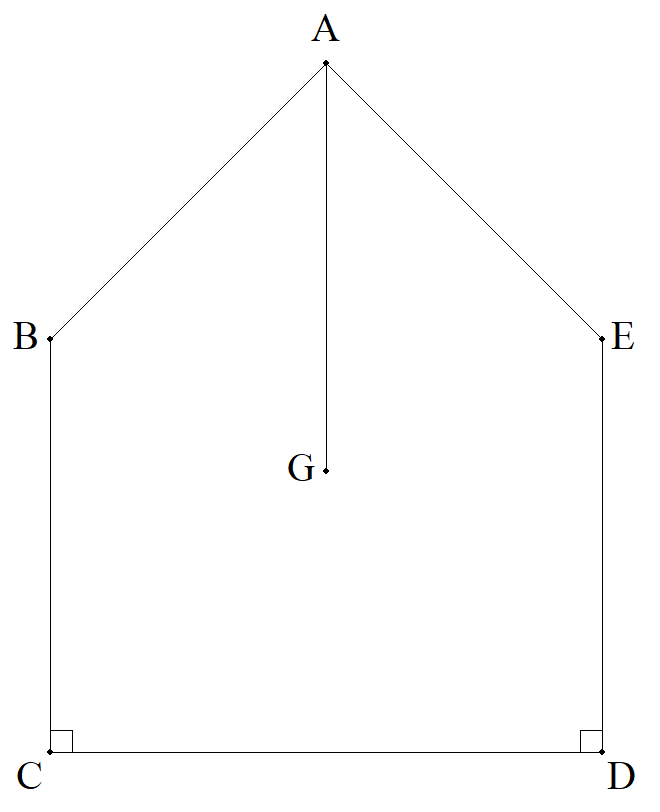



  15. 図の円O，Pの半径をそれぞれr1，r2，
    斜線部分の図形の重心をGとするとき，
    GOを求めよ。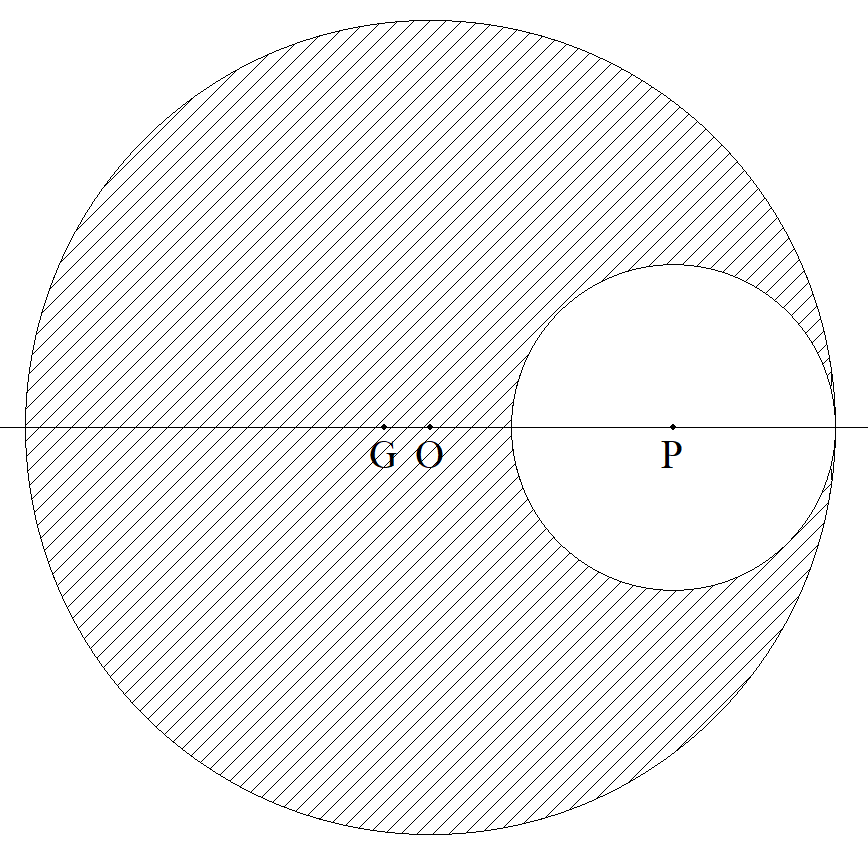



  16. 0＜k＜1とする。
    面積がSである平行四辺形ABCDについて，
    ADをk:(1-k)に内分する点をE，
    BEをk:(1-k)に内分する点をF，
    CFをk:(1-k)に内分する点をG，
    DGをk:(1-k)に内分する点をHとする。
    (1)　EB∥DGを証明せよ。
    (2)　四角形EFGHの面積が(3/8)Sとなるとき，
    　　kの値を求めよ。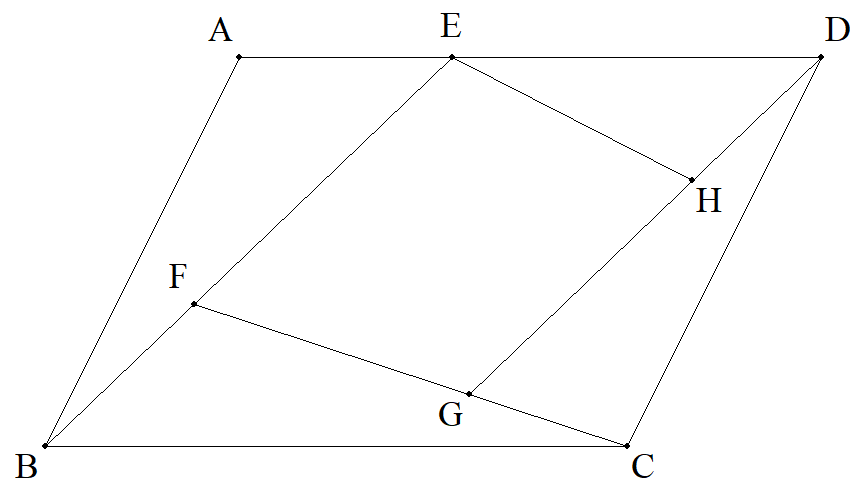



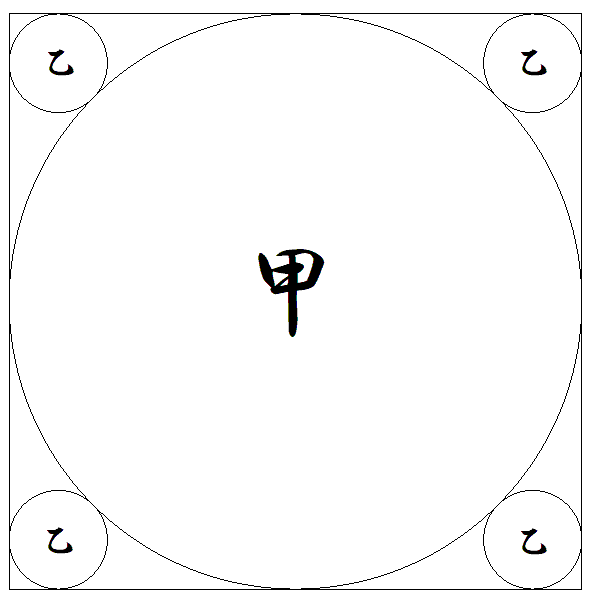
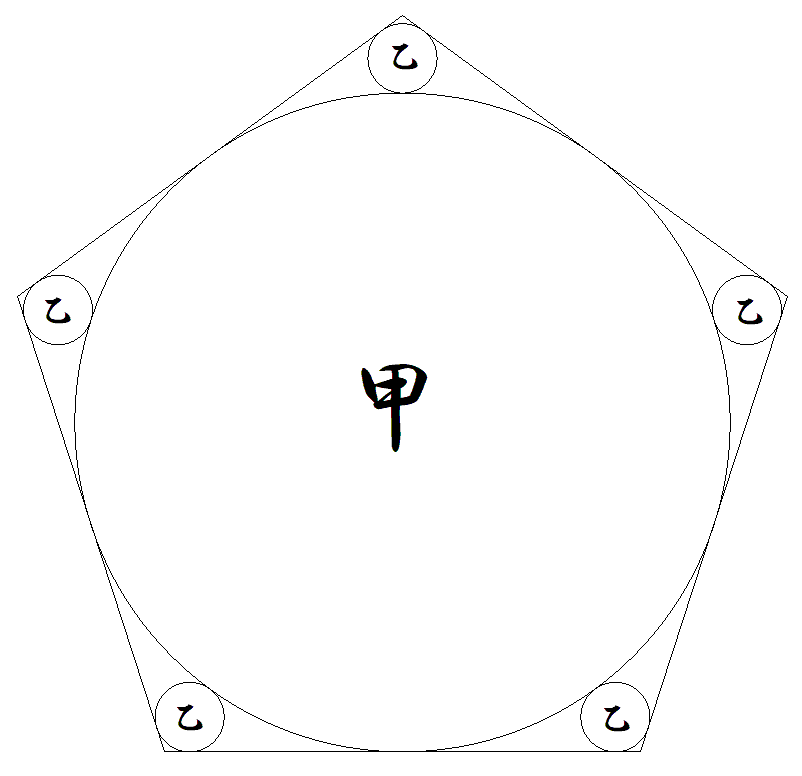
  17. 正n角形の内接円甲の半径をr1，その甲円と正n角形の隣り合う2辺に接するn個の乙円の半径をr2とする。
    r2/r1の値を求めよ。
    　 　


  18. 次の8か所の□に，＋，－，×を入れて100を表す式を13通りつくれ。なお，使わない演算記号があってもよい。
    1□2□3□4□5□6□7□8□9


  19. y=1/sinx+1/cosx+1/tanx+tanxの値域を求めよ。


  20. 右図のAからIは1から9までのどれかの数で，
    A+B=C，D×E=F，B+E=H，C+E=Gのとき，
    AからIの値を求めよ。



  21. 8文字のbaseballを横一列に並べる順列で，どのbもaの左側にくる確率を求めよ。


  22. 長方形ABCDの辺AB，BC，CD，DA上
    にそれぞれ点E，F，G，Hをとる。
    GからABに下した垂線の足をI，
    HからBCの下した垂線の足をJとする。
    AB＝a，AD＝b，EI＝c，FJ＝dのとき，
    四角形EFGHの面積を求めよ。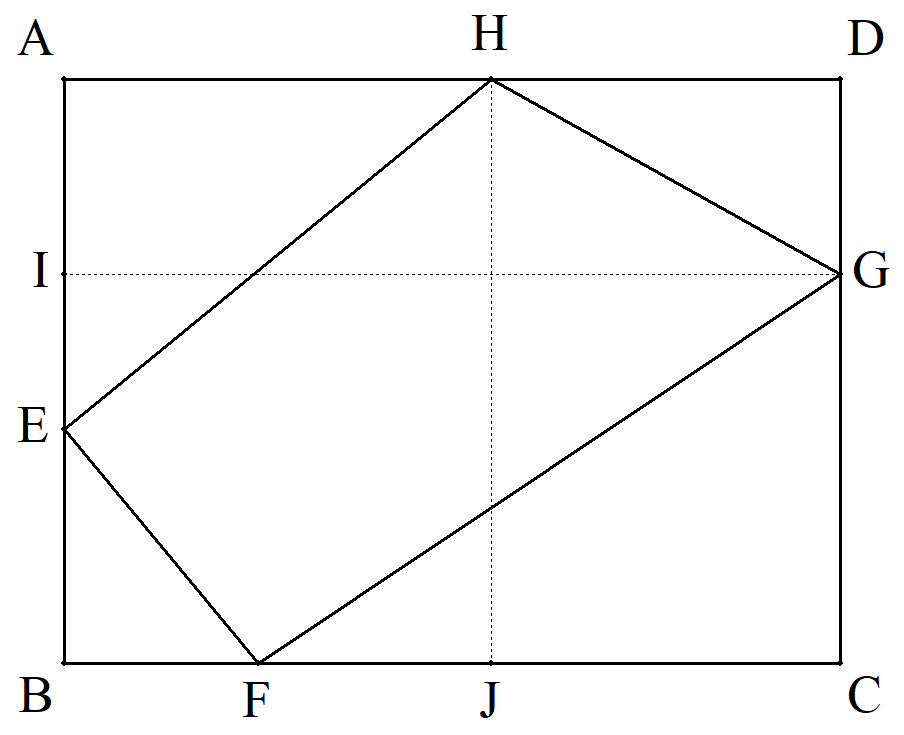



  23. 1～9までの数字をこの順にすべて使い，次の西暦を表す式をつくれ。
    ただし，使用できる記号は，四則演算と括弧のみで，1と2を結合した
    12のような使い方はできないものとする。
    (1)　2021
    (2)　2022


  24. AC＝2a，BD＝2bである菱形ABCD内に3個の甲円
    が図のように配置されている。
    甲円の半径を求めよ。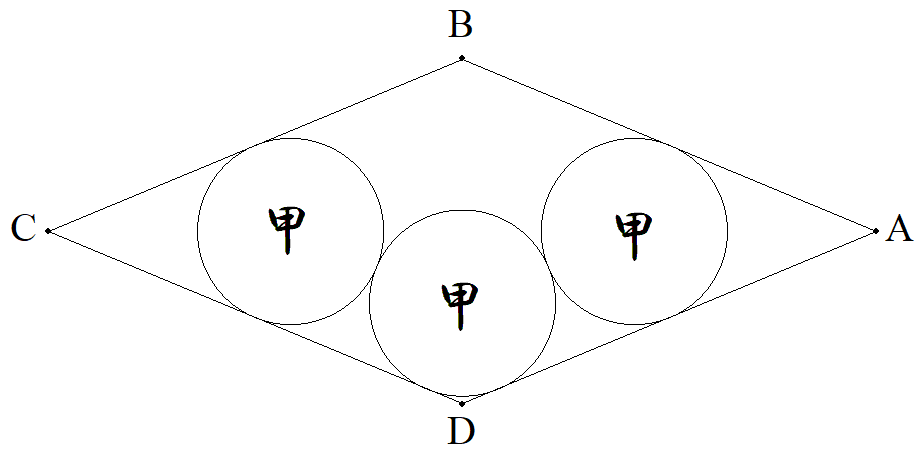



  25. aは実数の定数である。
    2次方程式(a2+1)x2-(a2+8a+1)x+2a2+2=0は重解αをもつ。
    このとき，α2の値を求めよ。


  26. △ABCの頂点A，B，Cから対辺に下した垂線の足をそれぞれD，E，Fとする。
    BD＝10，DC＝2，CE＝3のとき，AFを求めよ。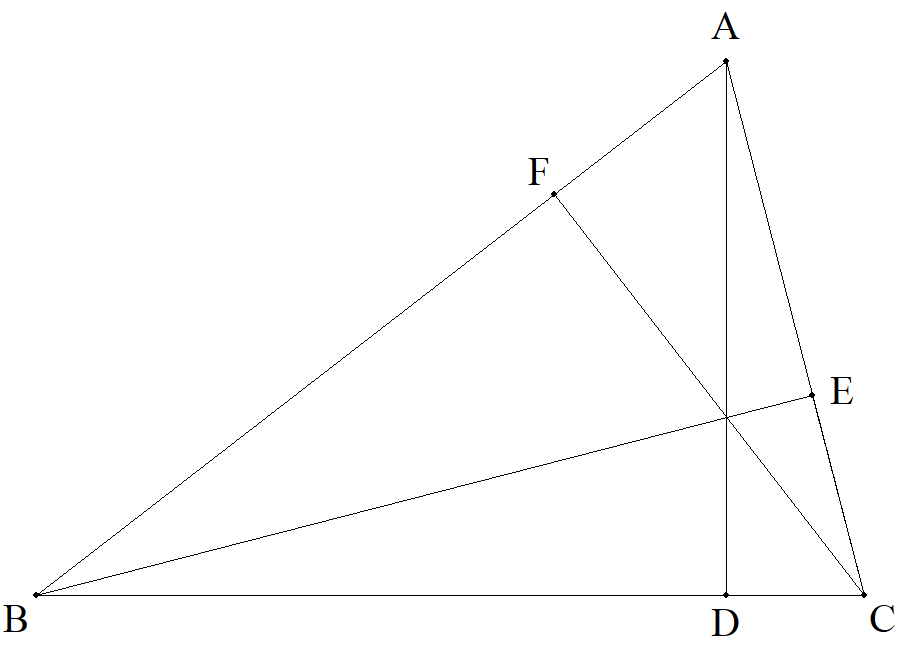



  27. 図のように甲乙円2個ずつが配置されており，
    どの3個の円も1点で交わり，その交点はひし
    形になっている。
    甲乙円の半径をそれぞれR1，R2（R1＞R2）
    とするとき，ひしの対角線をぞれ求めよ。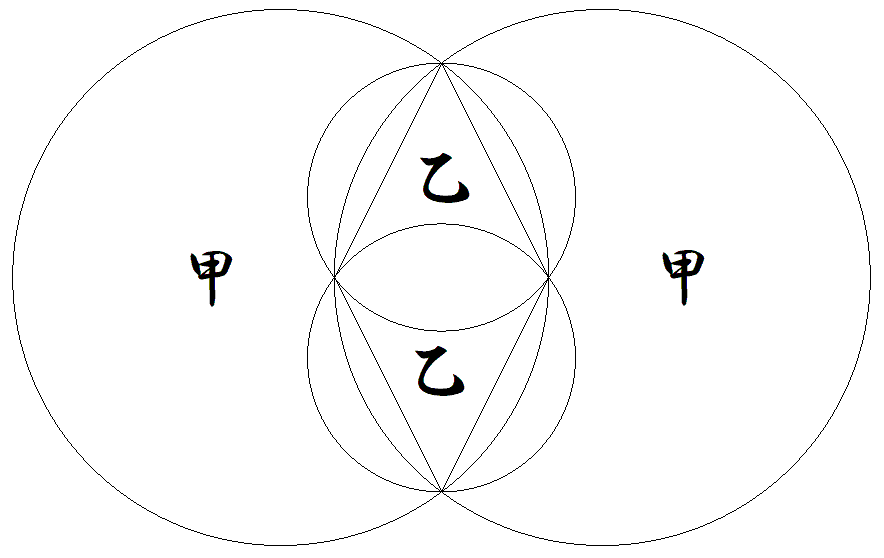



  28. 図のように2個ずつの甲乙円が1点で交わり，
    甲円同士，乙円同士は，それぞれ接している。
    また，甲乙円を取り囲む四角形がひし形になっ
    ている。
    甲乙円の半径をそれぞれr1，r2（r1＜r2）と
    するとき，ひし形の対角線をそれぞれ求めよ。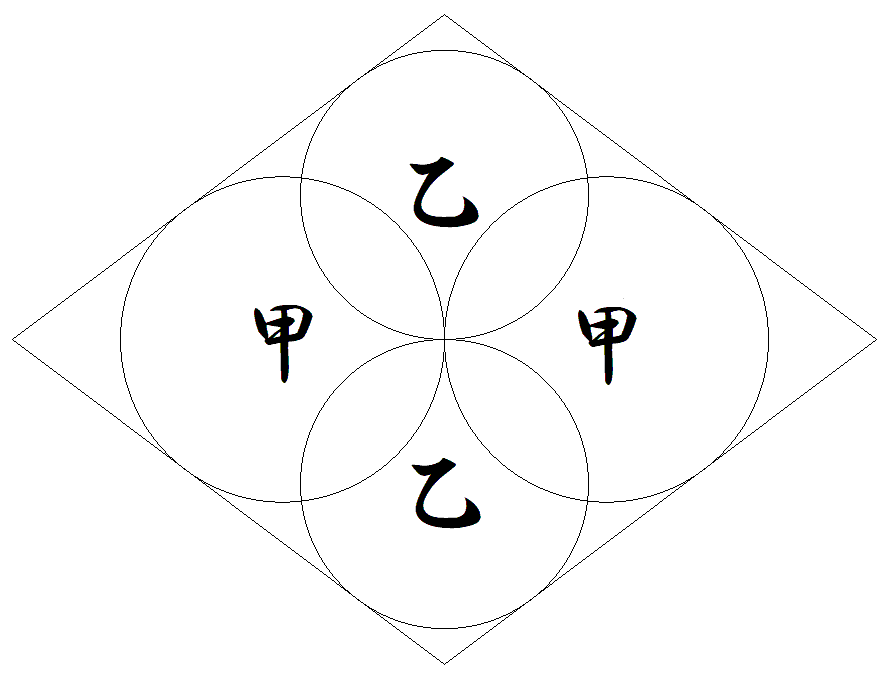



  29. ひし形の中心を通る甲乙円2個ずつが図のように
    配置されている。
    甲乙円の直径の逆数の差とひし形の対角線の逆数
    の差は等しくなることを証明せよ。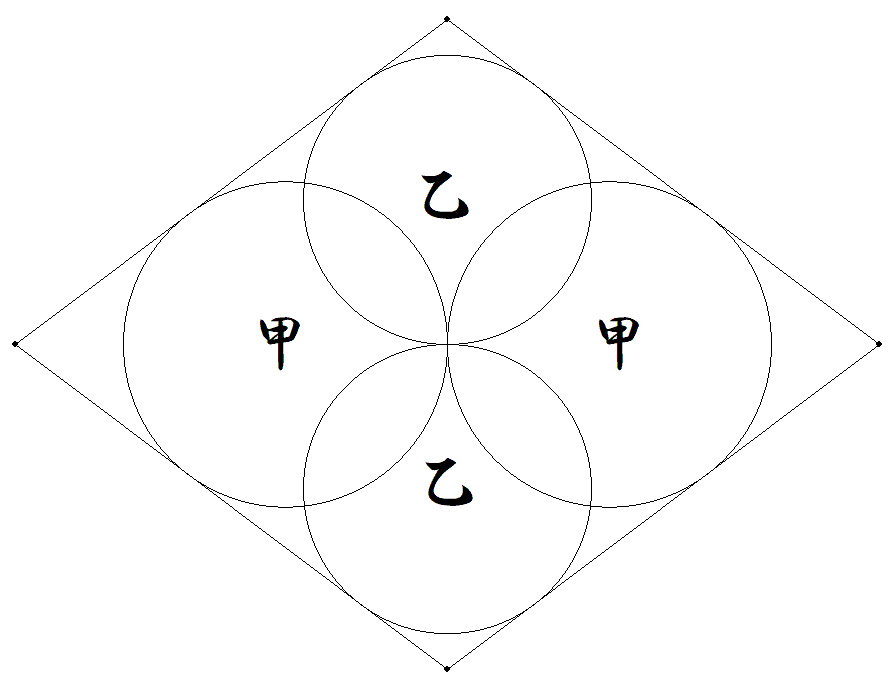



  30. 円に内接する四角形ABCDの対角線の交点Eから
    AB，BC，CD，DAに下した垂線の足をそれぞれ
    P，Q，R，Sとすると，PQ＋RS＝SP＋QRとな
    ることを証明せよ。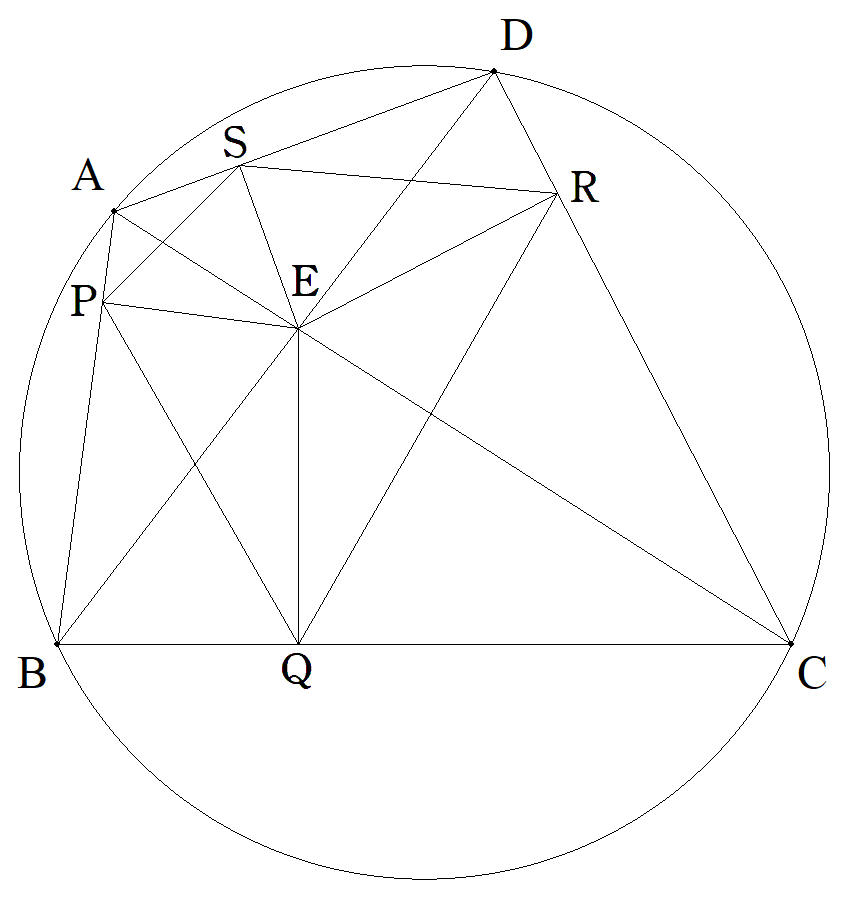



  31. 長方形ABCDのCD，DA上にそれ
    ぞれ点E，Fをとる。
    EからBFに下した垂線の足をG，
    FからBEに下した垂線の足をH，
    BCとGEの交点をI，
    BAとHFの交点をJとする。
    このとき，次を示せ
    (1)　3点I，D，Jは同一直線上にある。
    (2)　△BIJ≧長方形ABCD×2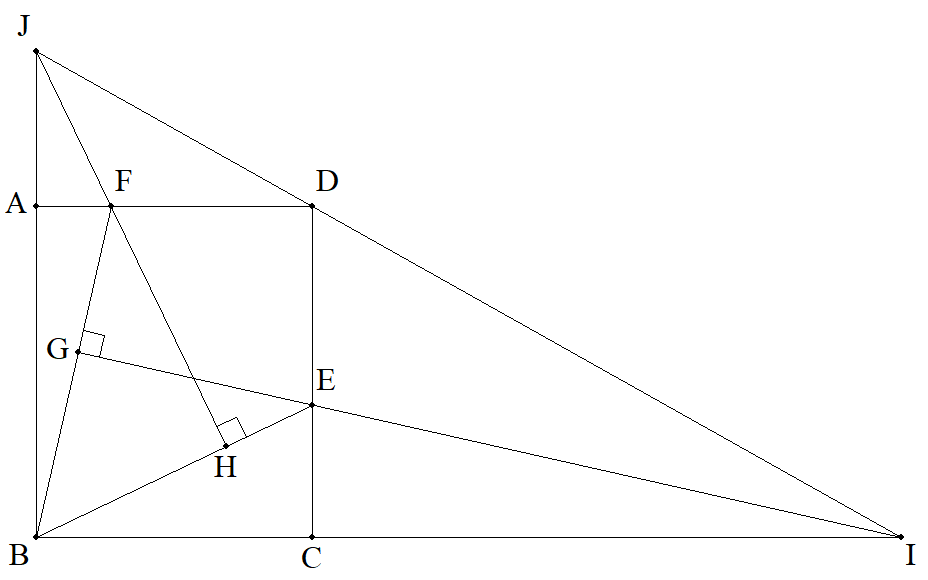



  32. △ABC内の点Gについて，AGとBC，BGと
    CA，CGとABの交点をそれぞれD，E，Fと
    するとき，GD/AD＋GE/BE＋GF/CF=1を
    証明せよ。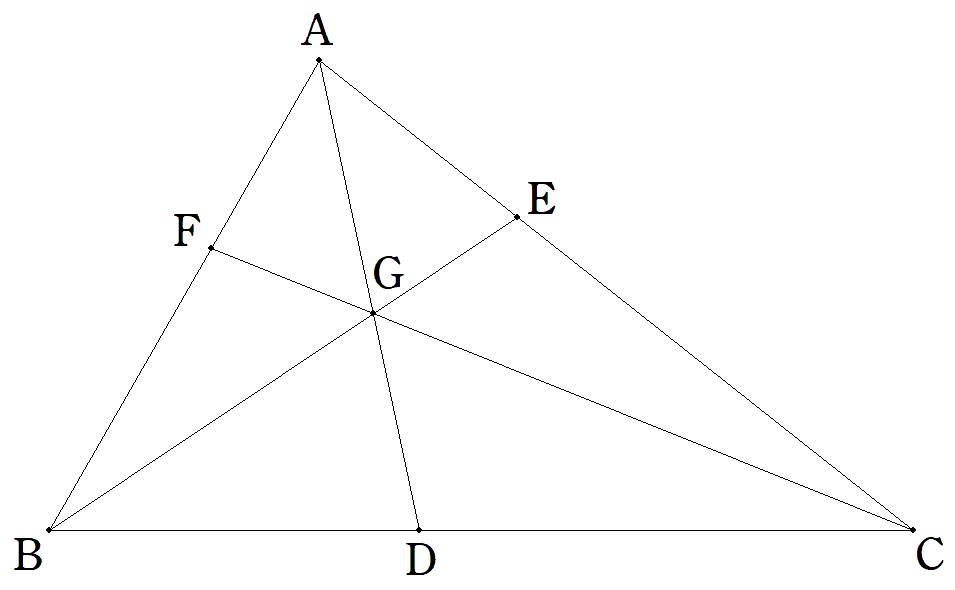



  33. 1辺の長さが1である正方形ABCDの
    AB，BC，CD，DAの中点をそれぞれ
    E，F，G，Hとする。
    次の図形の面積をそれぞれ求めよ。
    (1)　桃色の三角形（1個）
    (2)　黄緑色の四角形（1個）
    (3)　黄色の三角形（1個）
    (4)　水色の四角形（1個）
    (5)　紫色の正8角形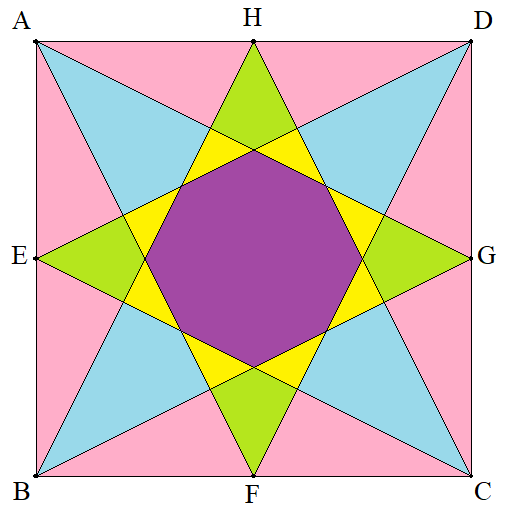



  34. 面積Sの平行四辺形ABCDの
    AB，BC，CD，DAの中点を
    それぞれE，F，G，Hとする。
    黄色の星形の面積をS´とする
    とき，S´/Sの値を求めよ。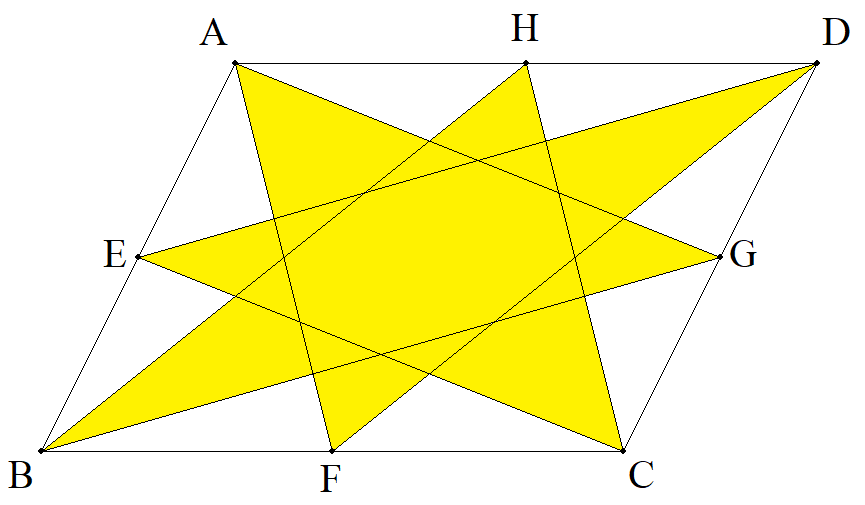



  35. △ABCの外心をO，垂心をH，AからBCに下した垂線の足
    をD，BCの中点をMとする。
    四角形OHDMが，MO＝p，OH＝qの長方形になるとき，
    BCをp，qを用いて表せ。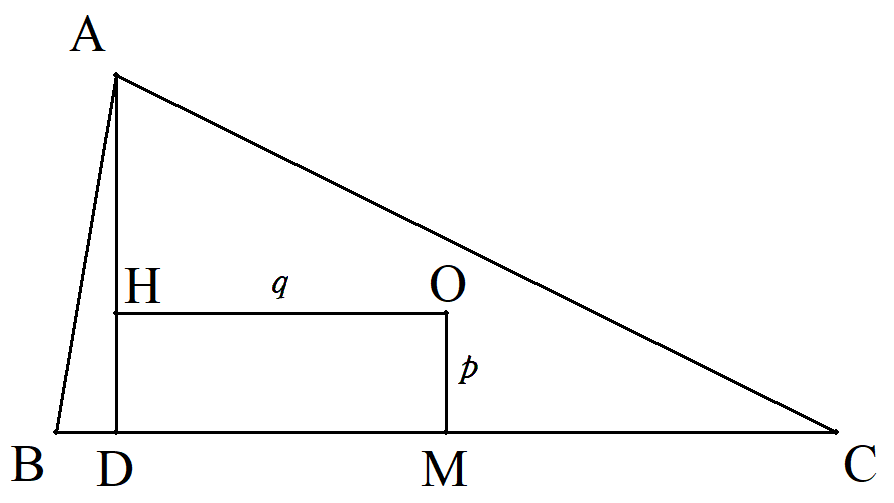



  36. AB，CDは円の異なる直径で，A，B，C，Dと異なる円周上の
    点PからAB，CDに下した垂線の足をそれぞれQ，Rとすると
    き，QRは一定であることを証明せよ。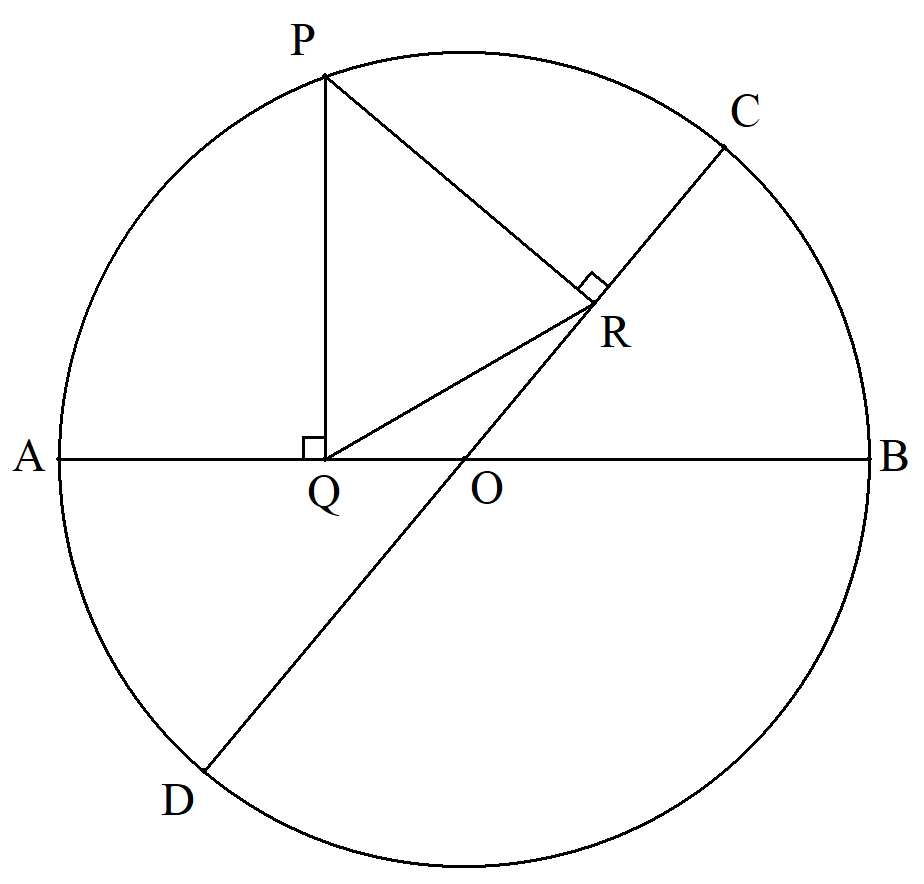






  38. 円に内接する八角形ABCDEFGHについて，
    AB＝CD＝EF＝GH＝a，
    BC＝DE＝FG＝HA＝bのとき，
    八角形の面積を求めよ。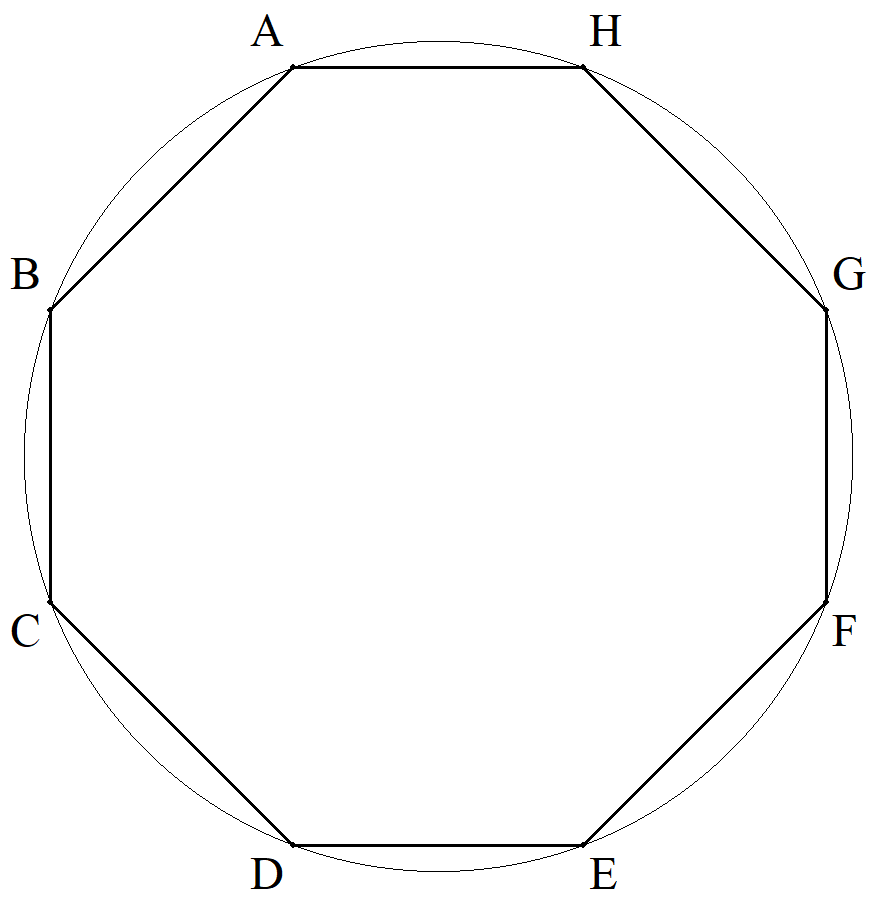



  39. 図のように直角二等辺三角形内に
    甲乙丙円を入れる。
    丙円の半径が1のとき，甲乙円の
    半径をそれぞれ求めよ。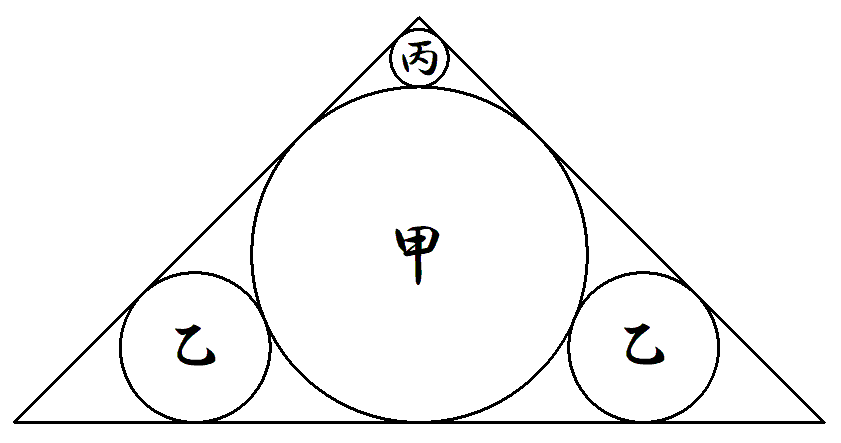



  40. 直角を挟む2辺の長さが1である
    直角二等辺三角形内に2本の斜線
    を引き，図のように甲乙円2個ず
    つ入れる。
    甲乙円の半径をそれぞれ求めよ。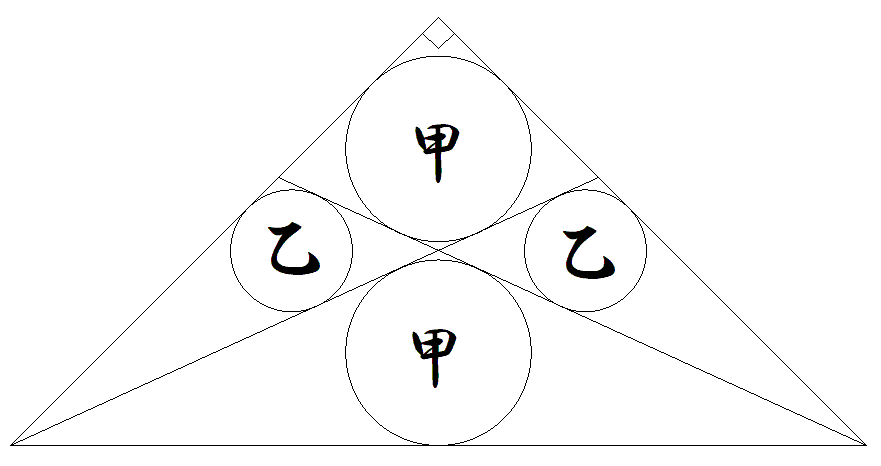



  41. 長方形に対角線を引き，その中に，図のように
    甲乙丙円を2個ずつ，丁円を4個入れる。
    長方形の縦を1，横をaとするとき，甲乙丙丁円
    の半径をそれぞれaを用いて表せ。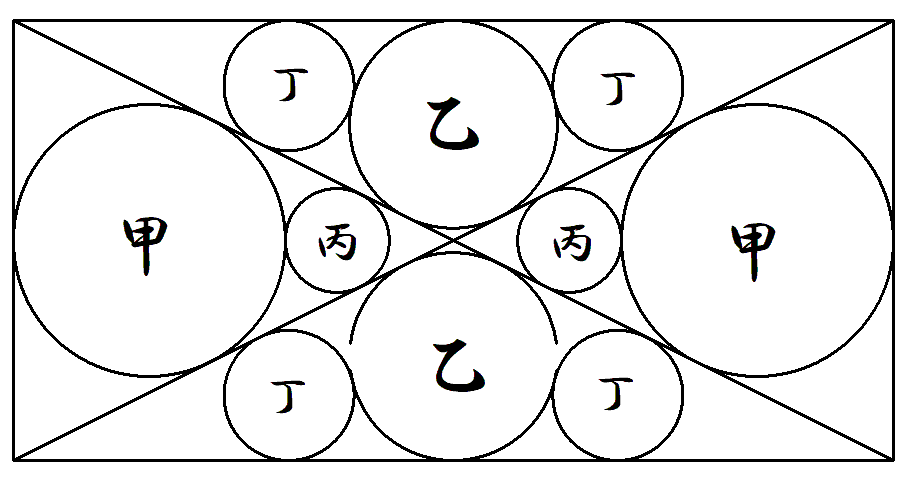



  42. 半径1の円内に，図のように甲円5個，
    乙円4個が入っている。
    甲乙円の半径をそれぞれ求めよ。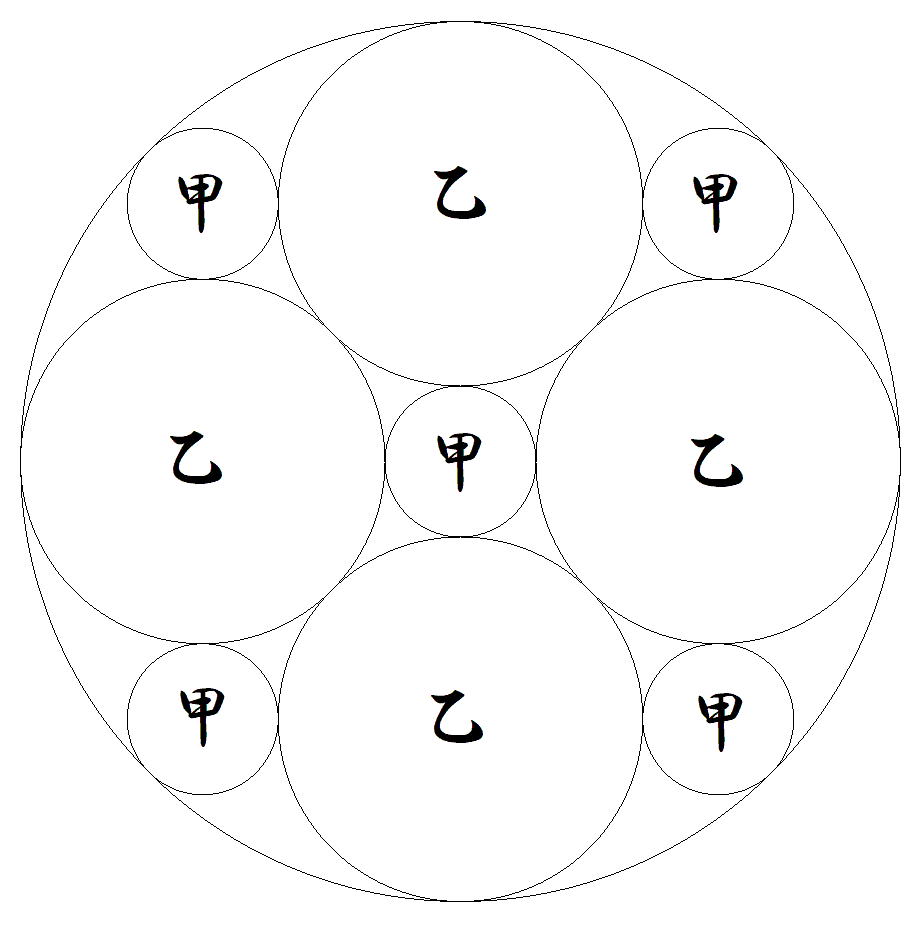



  43. 1辺の長さが1である正三角形内に
    2本の斜線を引き，図のように甲円
    2個，乙円2個を内接させる。
    このとき，甲乙円の半径をそれぞれ
    求めよ。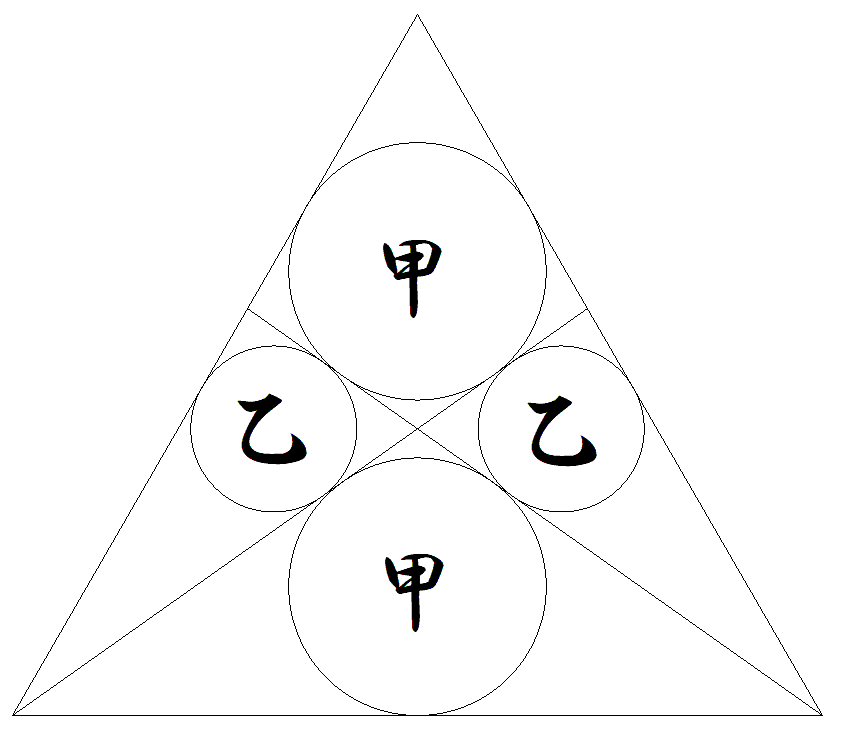



  44. 1辺の長さが1である正六角形と3個の
    等円が図のように配置されている。
    色のついた部分の面積の和を求めよ。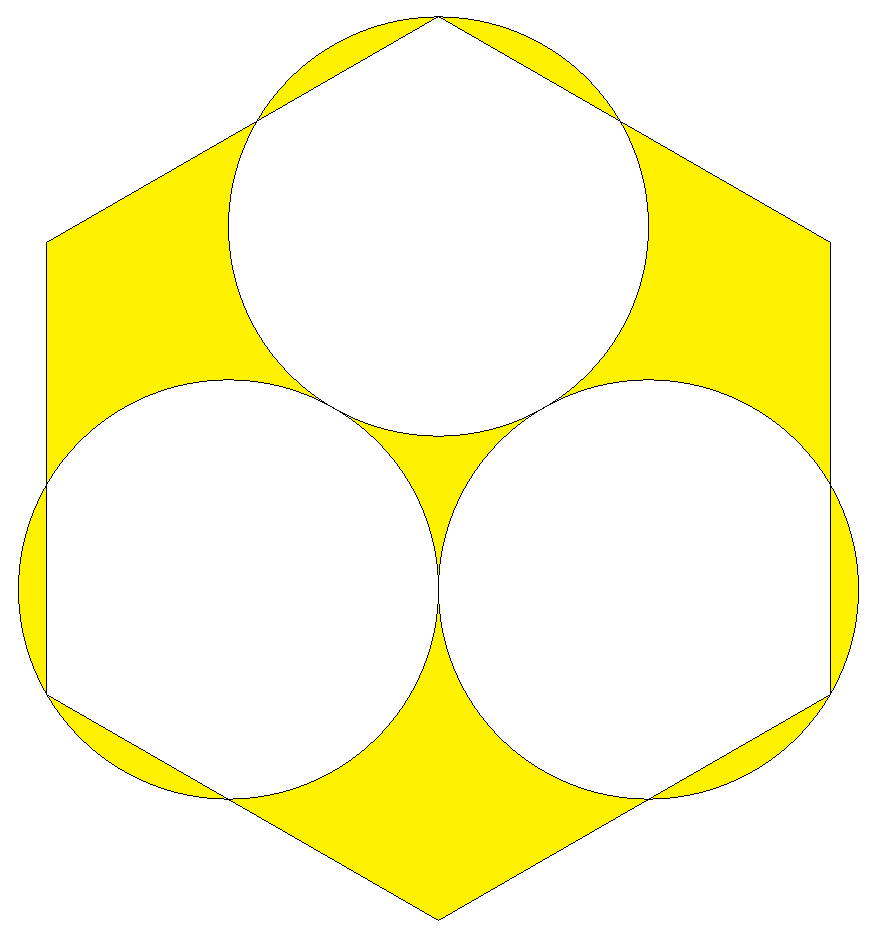



  45. 正三角形を重心を中心に180°回転させ，
    元の三角形との間に，図のように，甲円
    1個，乙円6個を接するように入れる。
    このとき，乙径＝甲径÷3を証明せよ。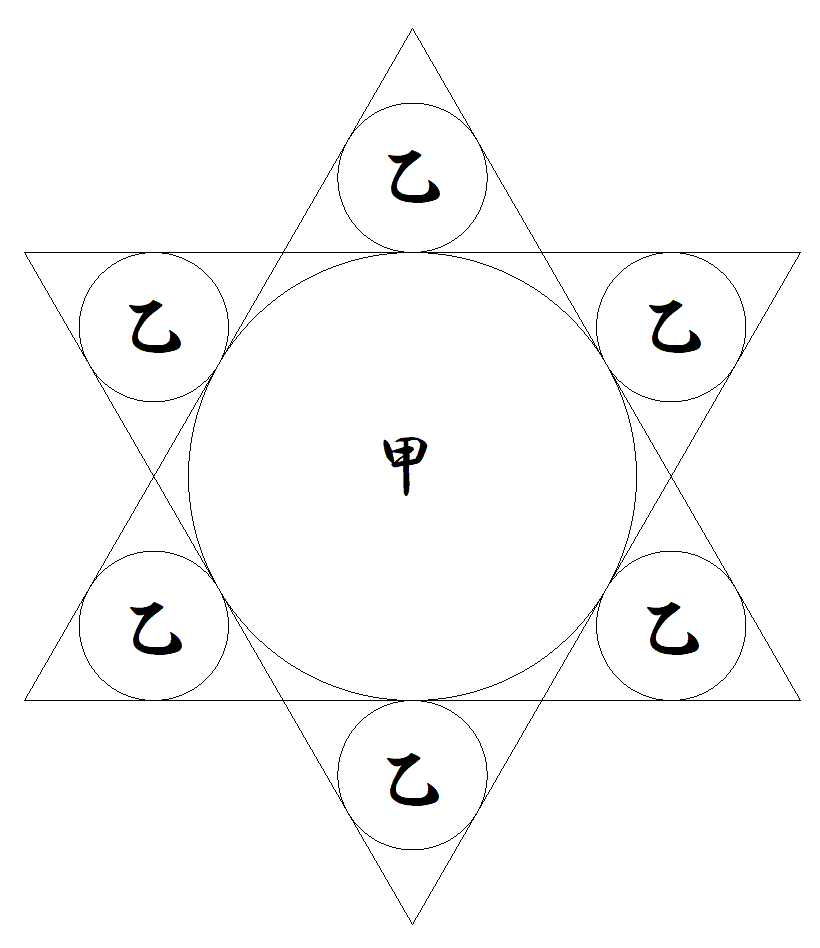



  46. 正三角形と大円と6個の小円が
    図のように配置されている。
    大円外の小円の中心は中線上
    にあり，大円内の小円は辺の
    中点で接している。
    大円，小円の半径をそれぞれR，
    rとするとき，R/rの値を求めよ。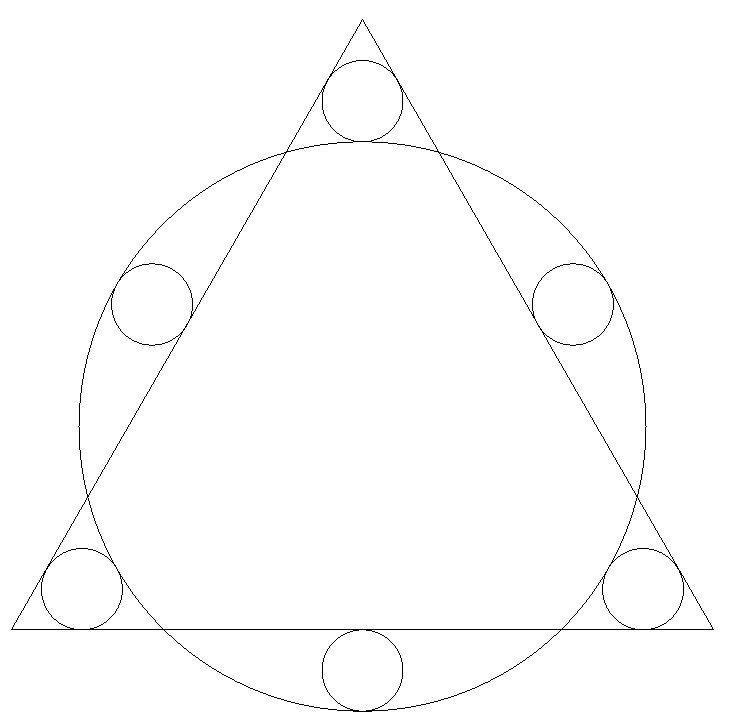



  47. 正方形と大円と8個の小円が図の
    ように配置されている。
    大円外の小円の中心は対角線上
    にあり，大円内の小円は辺の中点
    で接している。
    大円，小円の半径をそれぞれR，r
    とするとき，R/rの値を求めよ。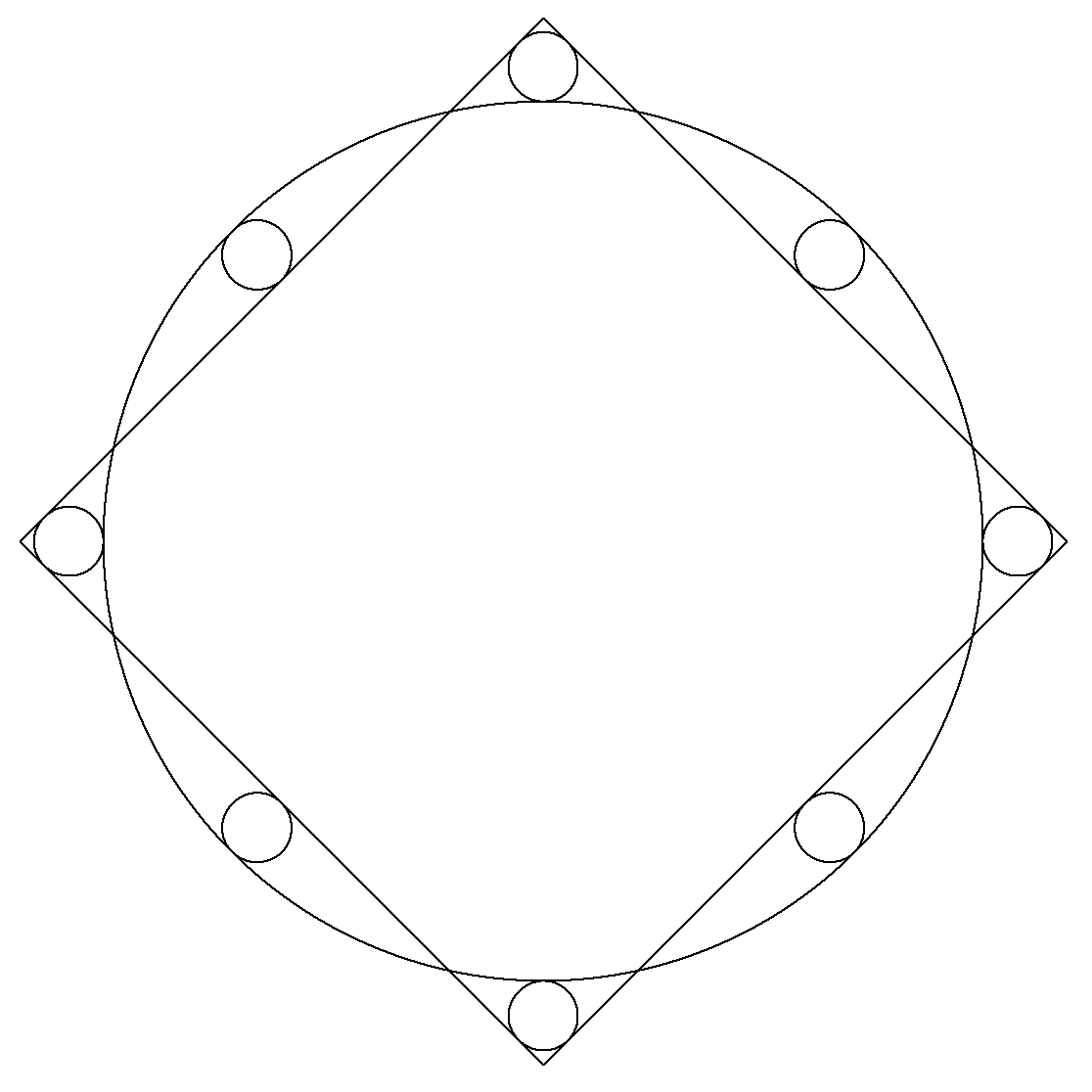



  48. 図のように，正三角形と大円と
    小円が配置されている。
    ただし，底辺の下に接している
    小円の個数はnである。
    大円，小円の半径をそれぞれR，r
    とするとき，R/rの値を求めよ。
    （図は，n=7の場合）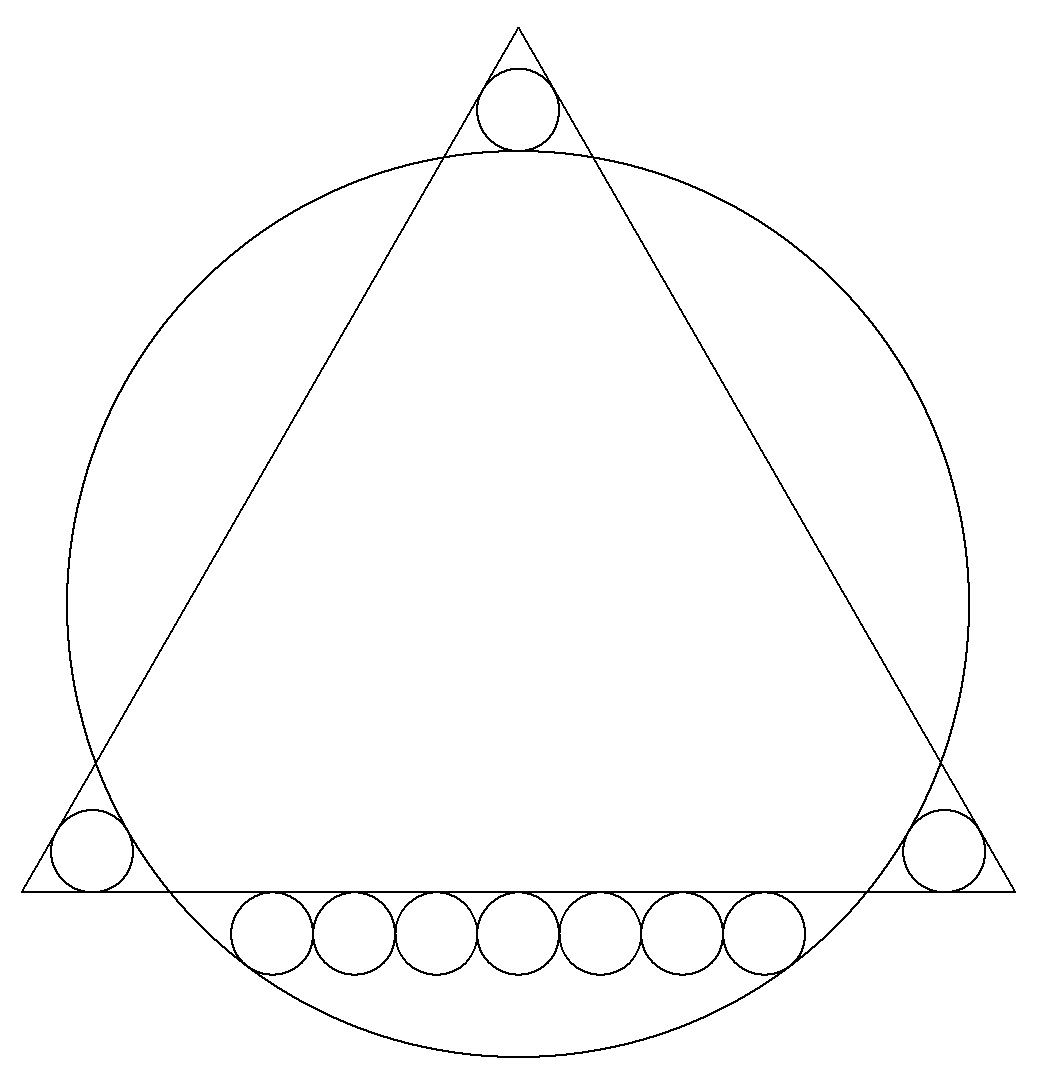



  49. 正n角形A1A2…Anの中心を中心とし，
    半径Rの大円と辺A1A2は，B1，B1´で
    交わる。
    2辺A1A2，A1Anに接し，大円に外接
    する小円の半径をrとする。
    B1B1´，弧B1B1´の間にk個の半径rの
    円が図のようにB1B1´に接して入って
    いる。k個の小円の両端の円は大円
    に接している。
    このとき，R/rの値を求めよ。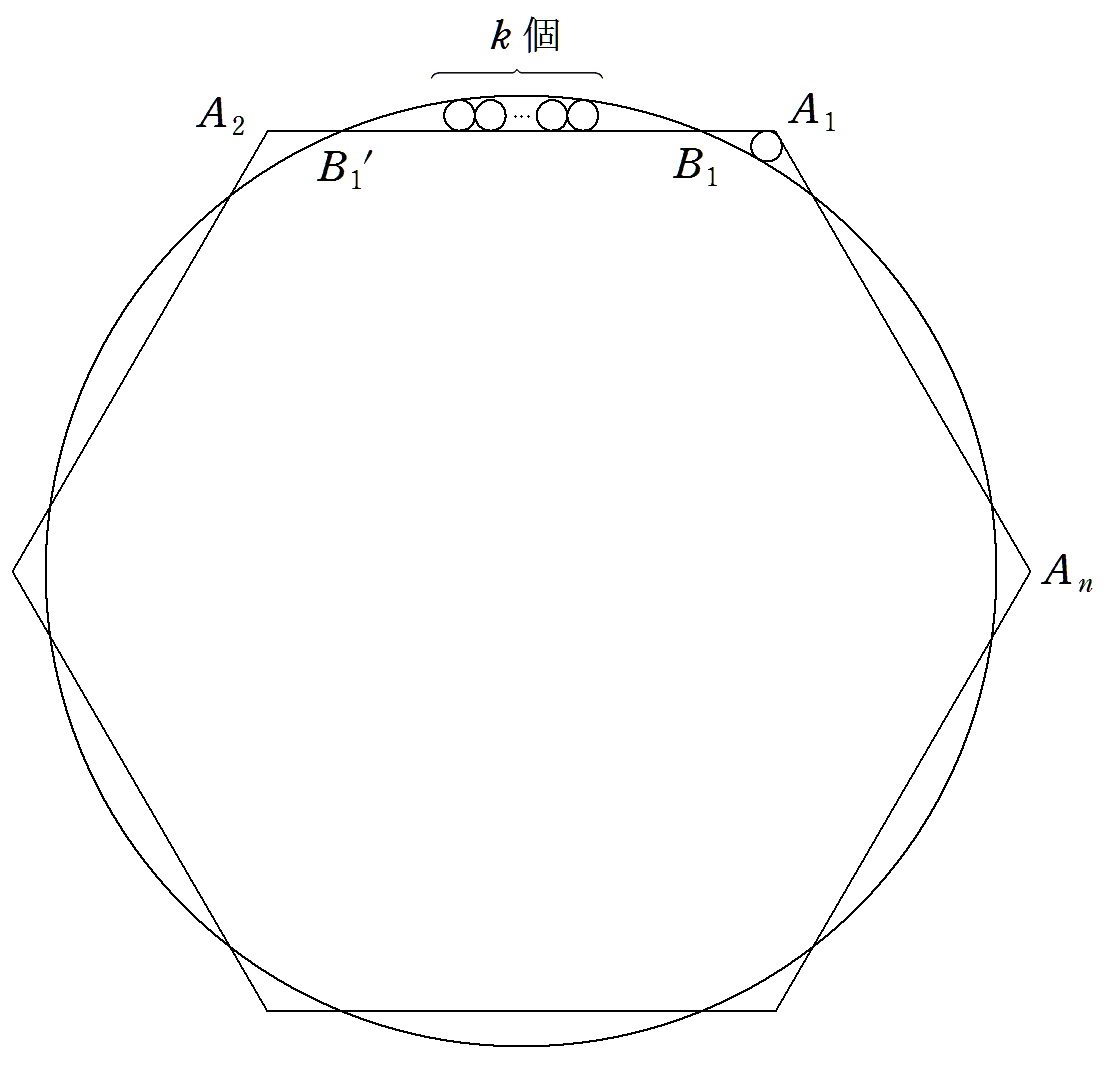



  50. 長方形に対角線を引き，その内部に，
    図のように，甲乙円2個ずつ，丙円
    6個を入れる。長方形の縦を1，横を
    aとしたとき，aの満たす整係数の
    方程式を一つ求めよ。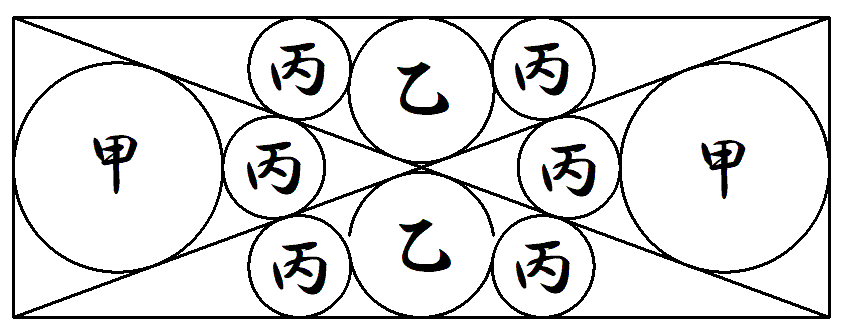