|
正三角形と大円と甲円と5個の乙円が 図のように配置されている。 甲円は辺の中点で接している。 このとき,次の値をそれぞれ求めよ。 (1) 甲円径÷乙円径 (2) 大円径÷乙円径 | 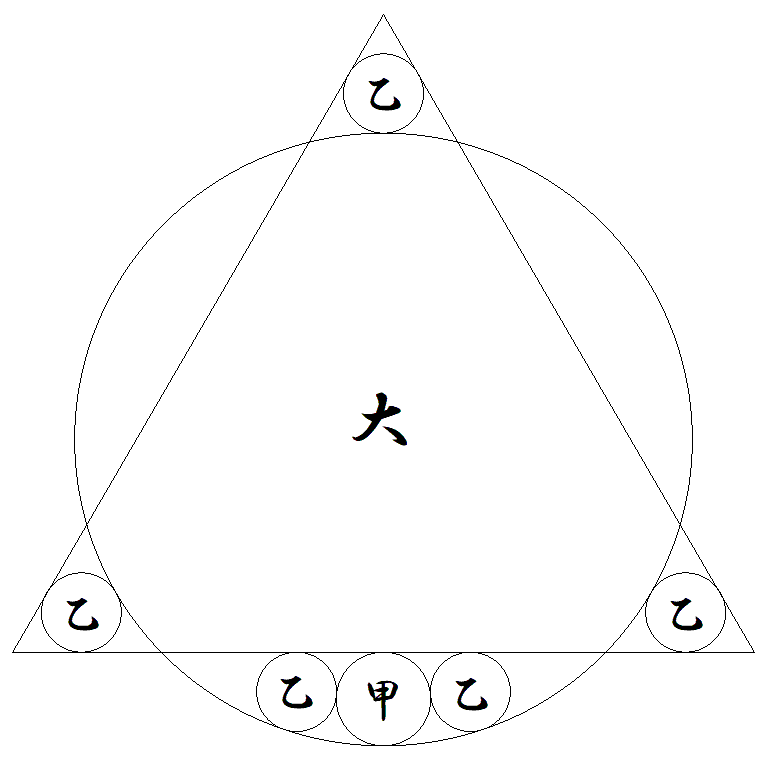 |
|
正方形と大円と甲円と6個の乙円が, 図のように配置されている。 甲円は辺の中点で接している。 このとき,次の値を求めよ。 (1) 甲円径÷乙円径 (2) 大円径÷乙円径 | 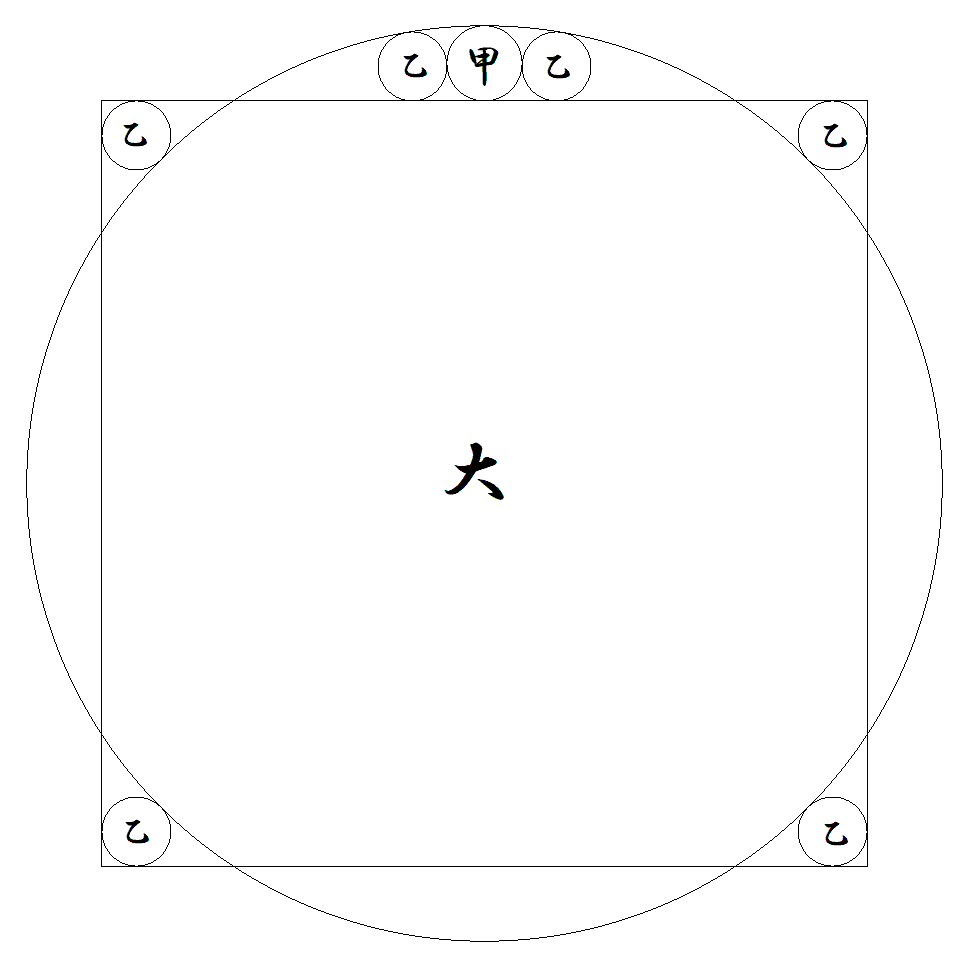 |
|
正奇数角形の外接円,内接円の半径を それぞれR,rとするとき,一番長い 対角線の長さをR,rを用いて表せ。 | 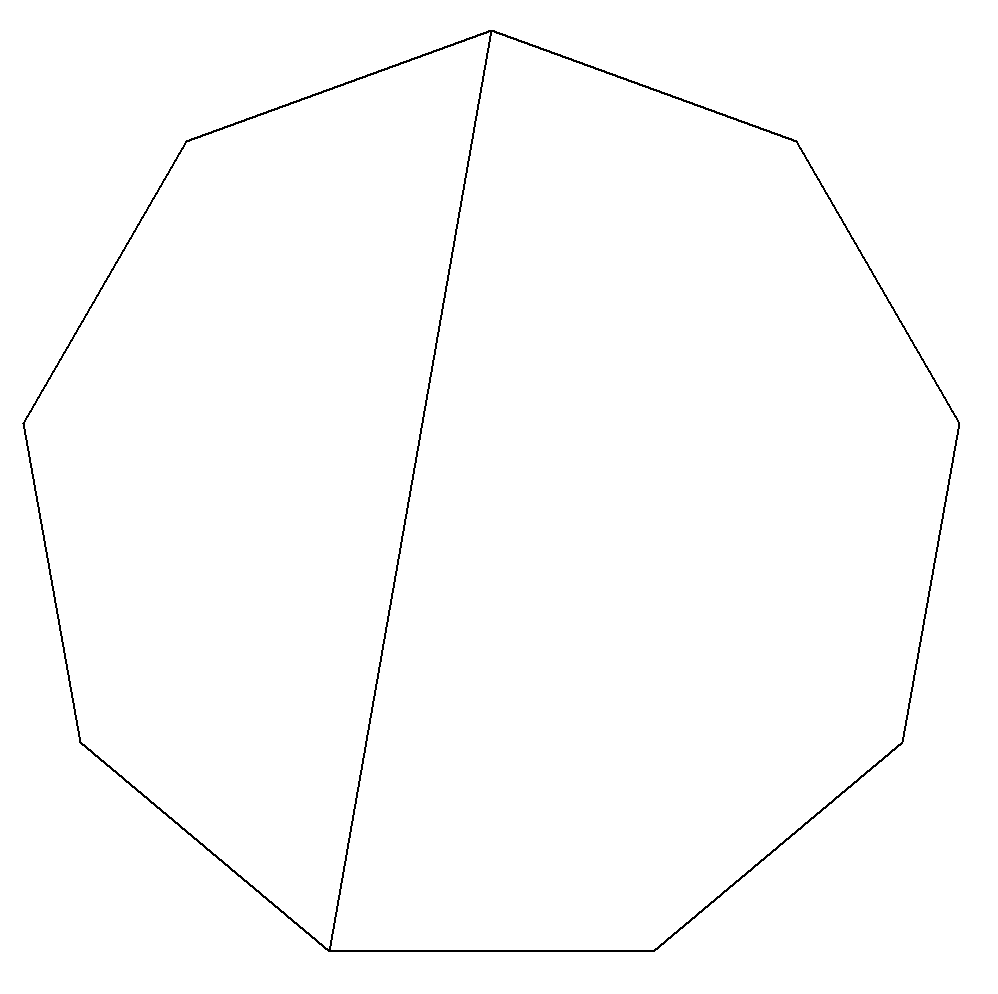 |
|
正三角形ABCについて,BC上に点Dをとり, AからBCに下した垂線の足をEとする。 △ABD,△ADCの内接円とBCとの接点をそれ ぞれF,Gとすると,FE=DCとなることを証明 せよ | 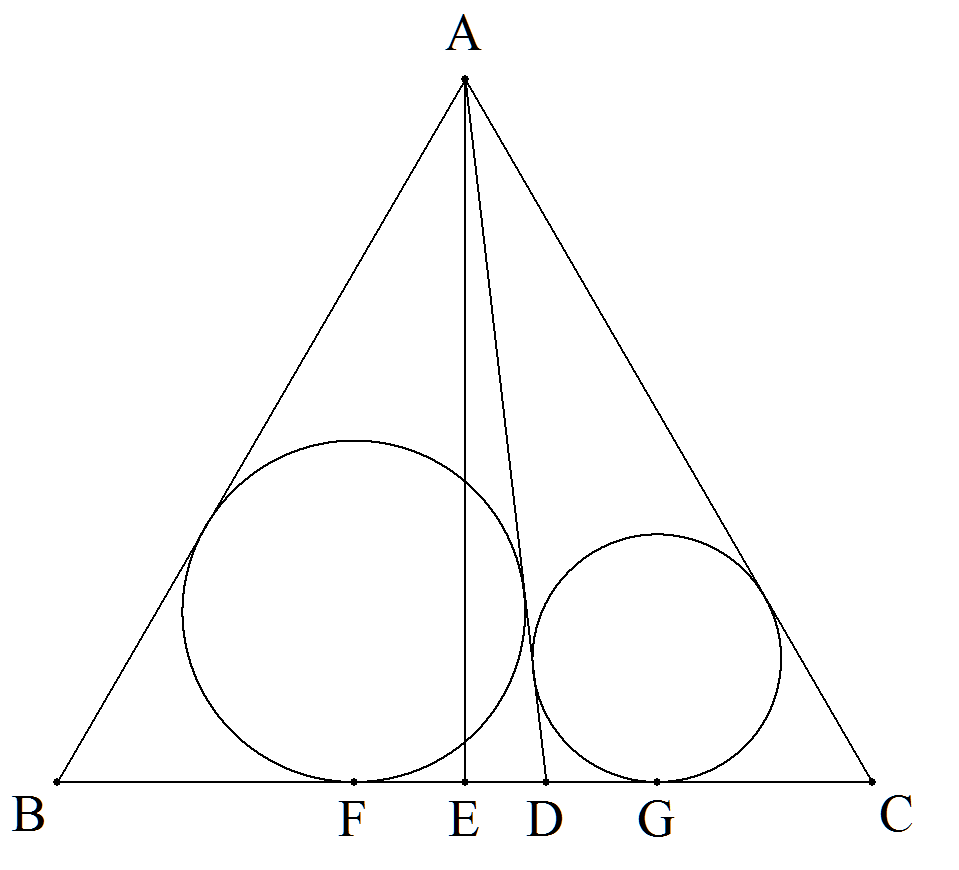 |
|
△ABCのBC上に点Pをとり,△ABP,△APCの内接円の共通外接線 (BCでない方)と,APとの交点をQとする。 PがBからCまで動くとき(P≠B,P≠C),点Qの軌跡を求めよ。 | 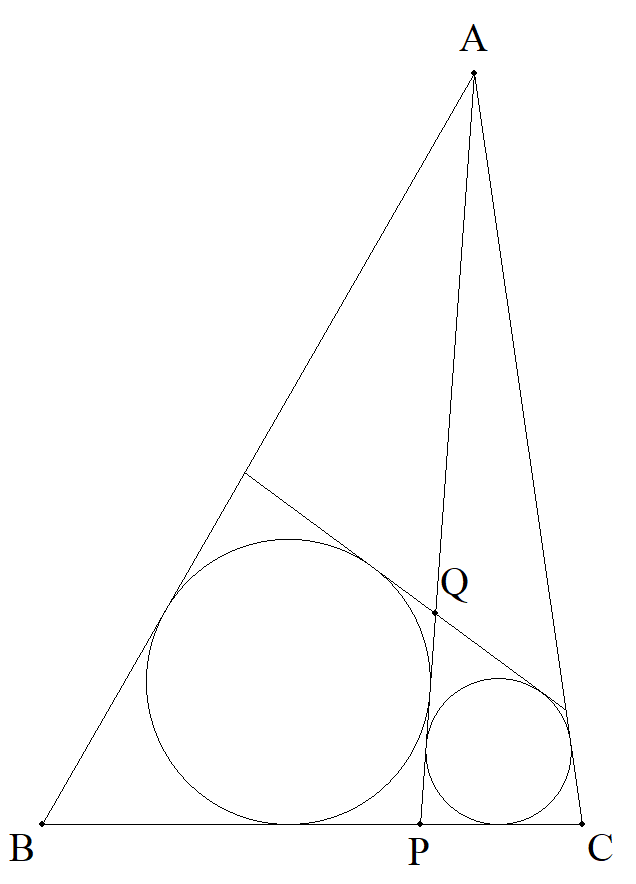 |
|
正三角形ABCのBC上に点Dをとり,△ABD,△ADCの 内接円をそれぞれO1(r1),O2(r2)とする。 2円O1,O2の共通外接線(BCでない方)とAB,AB, ADとの交点をそれぞれE,F,Gとする。 △AEG,△AGFの内接円をそれぞれO3(r3),O4(r4)と する。 r1=3,r2=2のとき, (1) ABを求めよ。 (2) AGを求めよ。 (3) r3を求めよ。 (4) r4を求めよ。 | 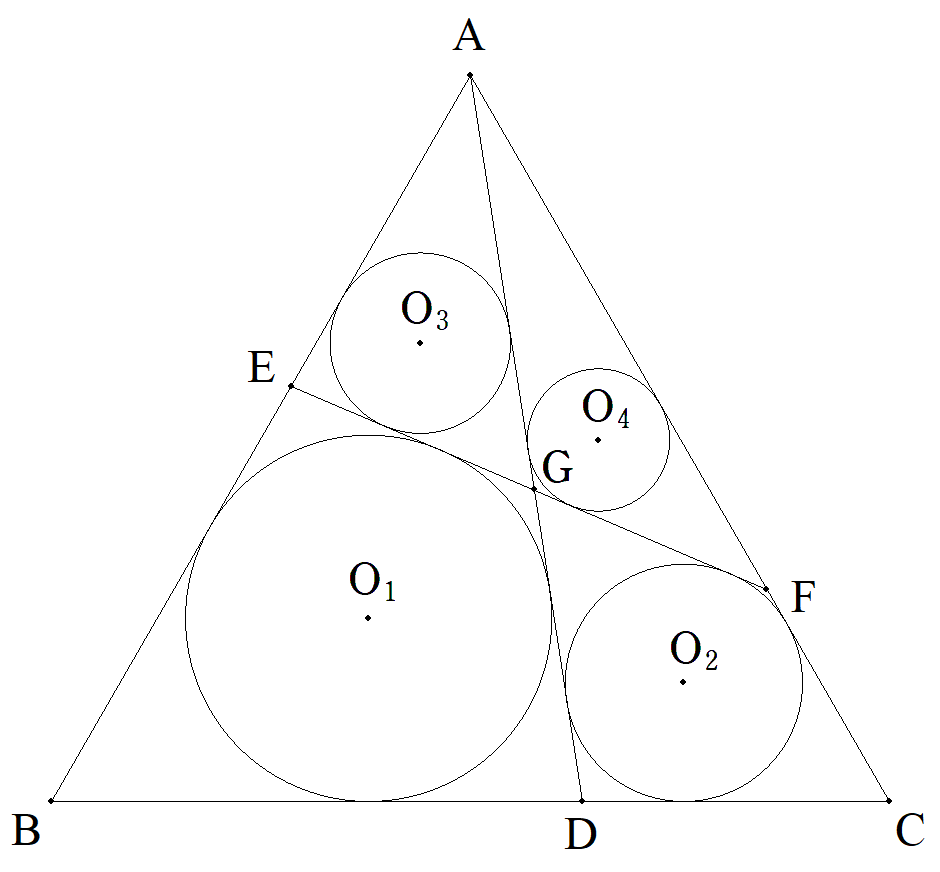 |
|
AB=a,AD=bである長方形ABCD内にABを直径とする半円 O1(r1)を描き,Dからこれに接線を引きBCとの交点をEとする。 △DECの内接円をO2(r2)とし,O1,O2の共通外接線(BCでな い方)とDC,DA,DEとの交点をそれぞれF,G,Hとする。 △DGH,△DHFの内接円をそれぞれO3(r3),O4(r4)とするとき, (1) r1,r2,r3,r4をそれぞれ求めよ。 (2) 1/r1-1/r2=1/r3-1/r4を示せ。 | 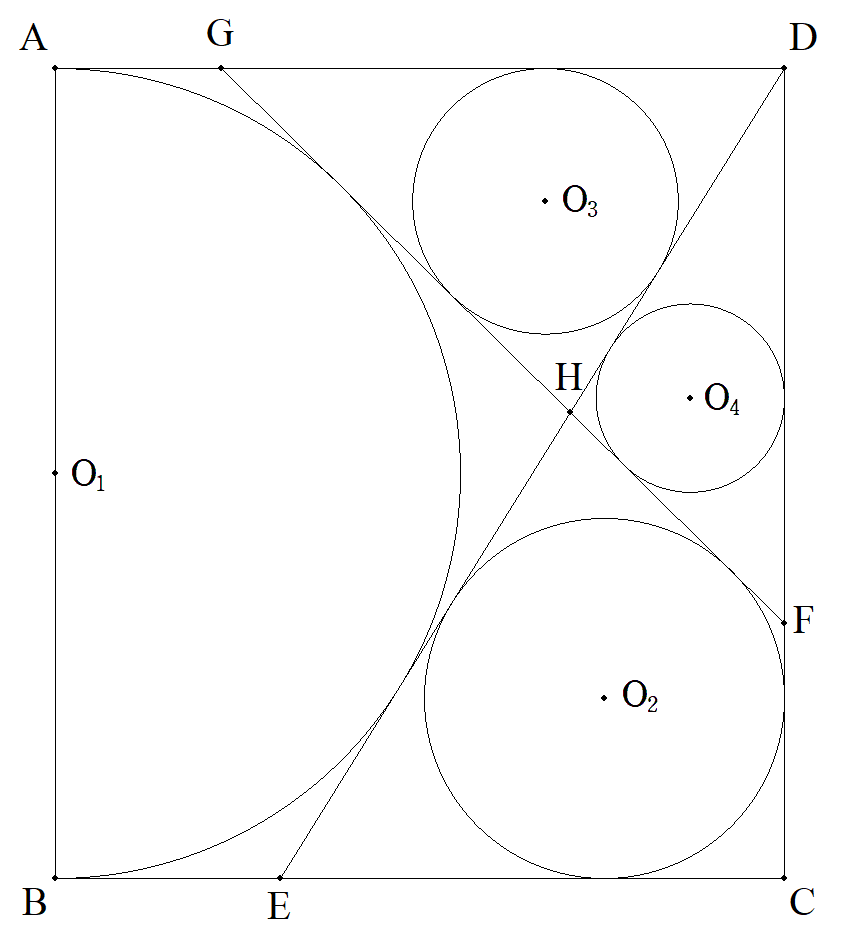 |
|
1辺の長さが1である正方形内に各頂点から等しい斜線を 引き,図のように甲円3個,乙円2個を入れる。 (1) 甲円の直径dの満たす3次方程式を一つ求めよ。 (2) 乙円の直径eの満たす3次方程式を一つ求めよ。 | 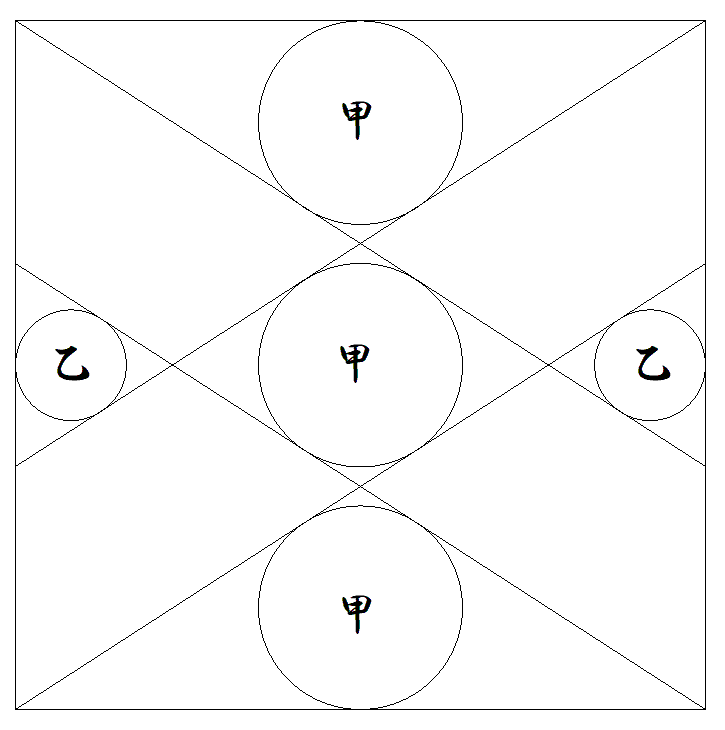 |
|
1辺の長さが1である正方形内に各頂点から等しい斜線を 引き,図のように甲円7個,乙円2個を入れる。 甲円,乙円の半径をそれぞれ求めよ。 | 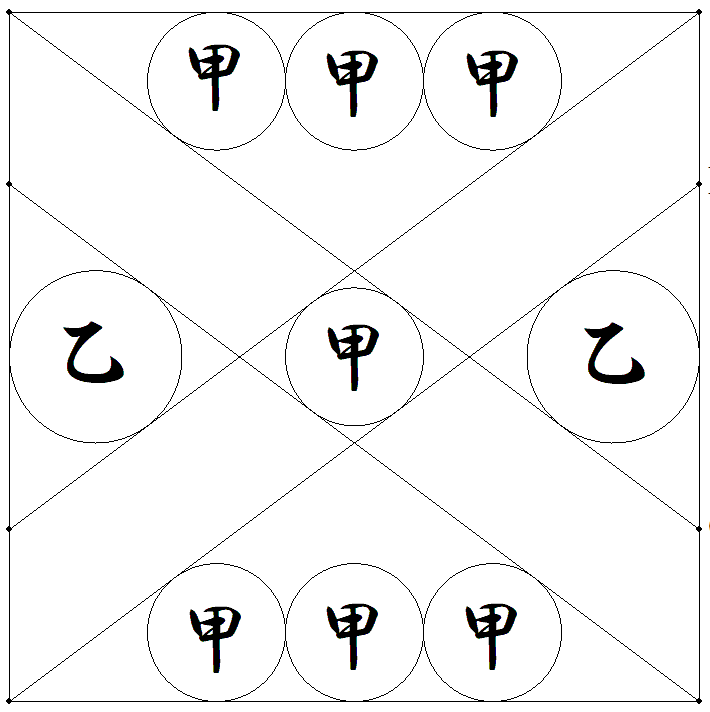 |
|
m,nを3以上の整数とする。 長方形ABCDの対角線の交点をEとする。 △ABEに内接するm個の連結した等円の半径はr1で, ABに接し,両端の円は,BE,EAに接している。 △EBCに内接するn個の連結した等円の半径はr2で, BCに接し,両端の円は,CE,EBに接している。 r1=r2のとき,AB:BCの比を求めよ。 | 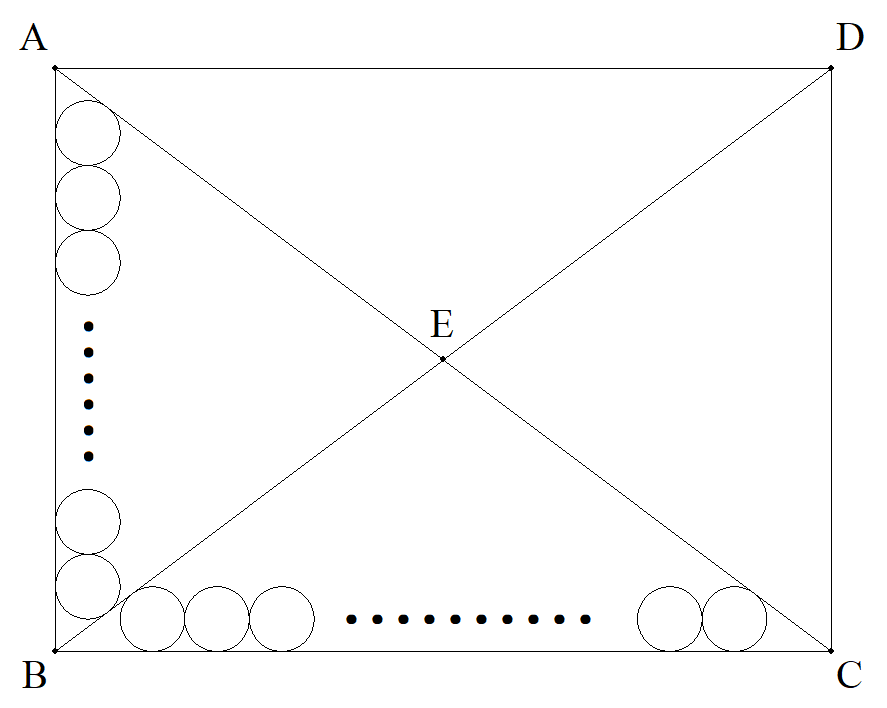 |
|
1辺の長さが1である正方形内に,頂点から 等しい斜線を2本引き,図のように正三角形 と2個の等円入れる。 正三角形の頂点は正方形の辺の中点にあり, 底辺は,正方形の辺に平行である。 上側の円は正三角形の内接円で,下側の円 は2本の斜線と正方形の辺に接している。 円の半径rの満たす最低次の方程式を一つ 求めよ。 | 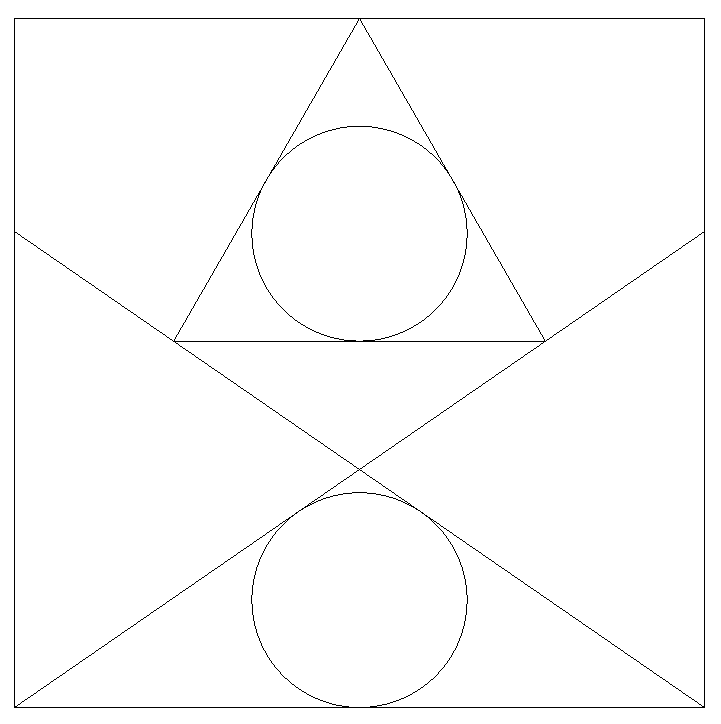 |
|
1辺の長さがaである正方形ABCDのDA上に点Eをとる。 △ABE,△DEC,△EBCの内接円をO1(r1),O2(r2),O3(r3)とする。 次の問いに答よ。 (1) 2円O1,O2の共通外接線(DAでない方)は円O3に接することを示せ。 (2) a2-4ar3+2r3(r1+r2)=0を示せ。 (3) r1+r2,r3のとりうる値の範囲をそれぞれ求めよ。 (4) a,r1が与えられたとき,r2,r3をそれぞれ求めよ。 | 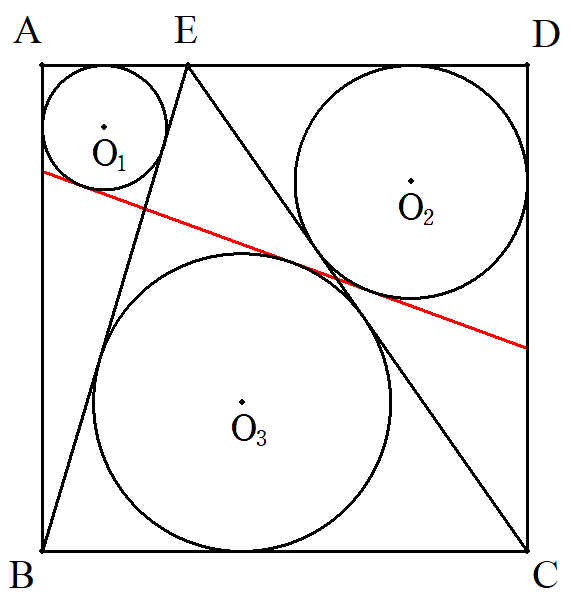 |
|
2円O1,O2はTで外接し,円O1は直線l1とAで接し, 円O2は直線l2とBで接している。l1∥l2のとき, 3点A,T,Bは共線であることを証明せよ。 | 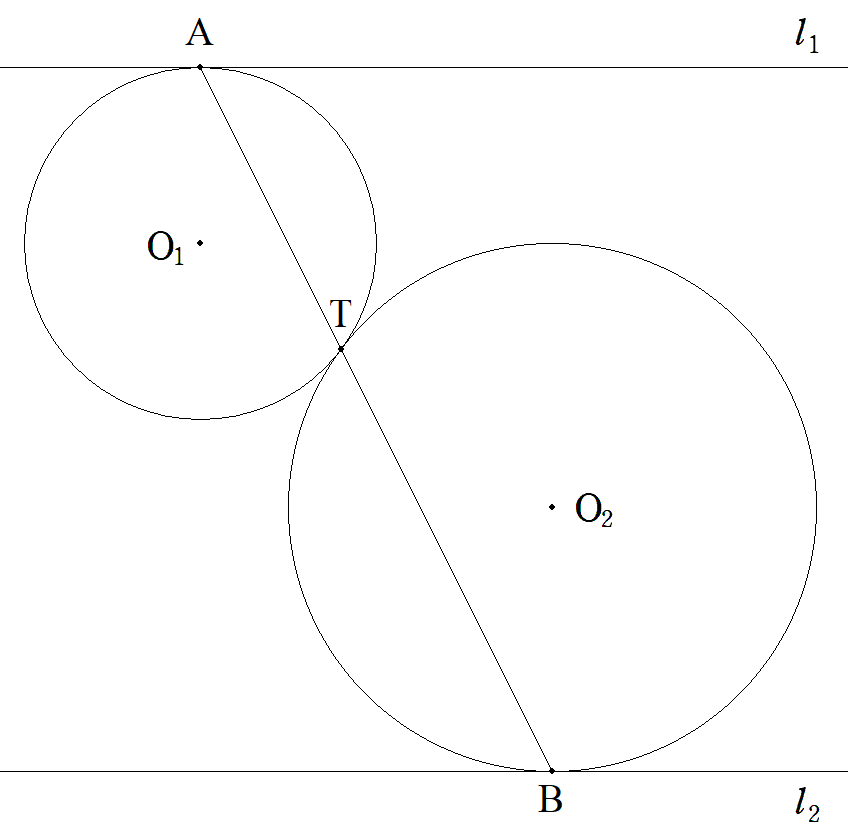 |
|
環状に接している甲円,乙円,丙円,乙円の4個の接点は, 共円であることを証明せよ。 | 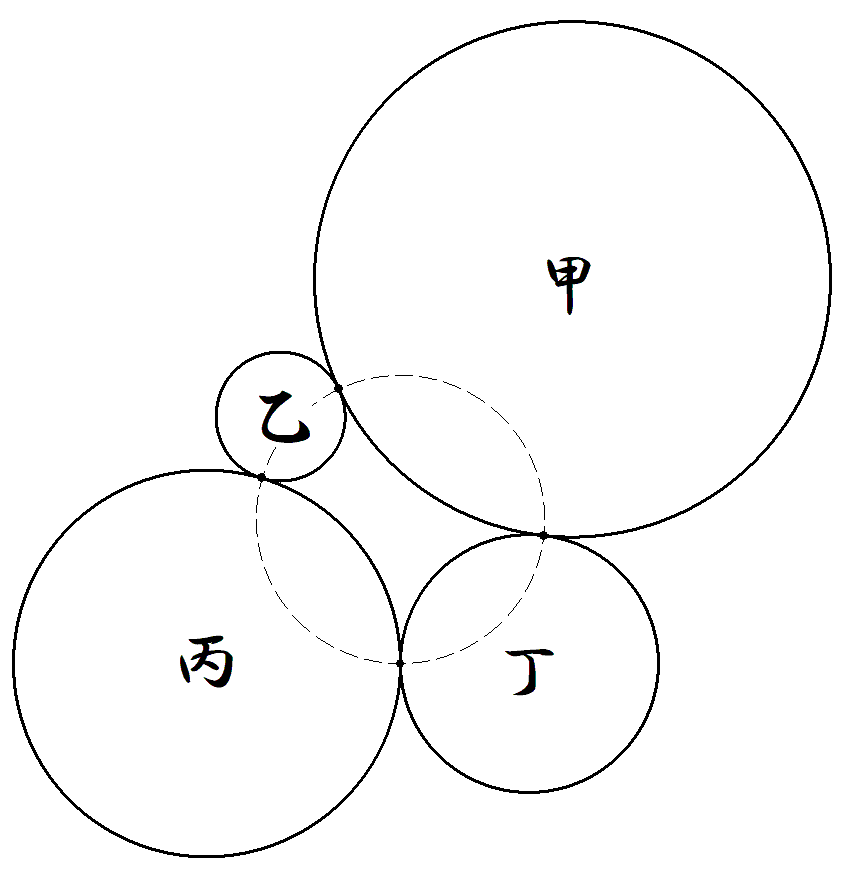 |
|
二等辺三角形内に直交する甲斜線,乙斜線を引き, 図のように,3個の等円を入れる。 乙斜線が2のとき,円の直径を求めよ。 | 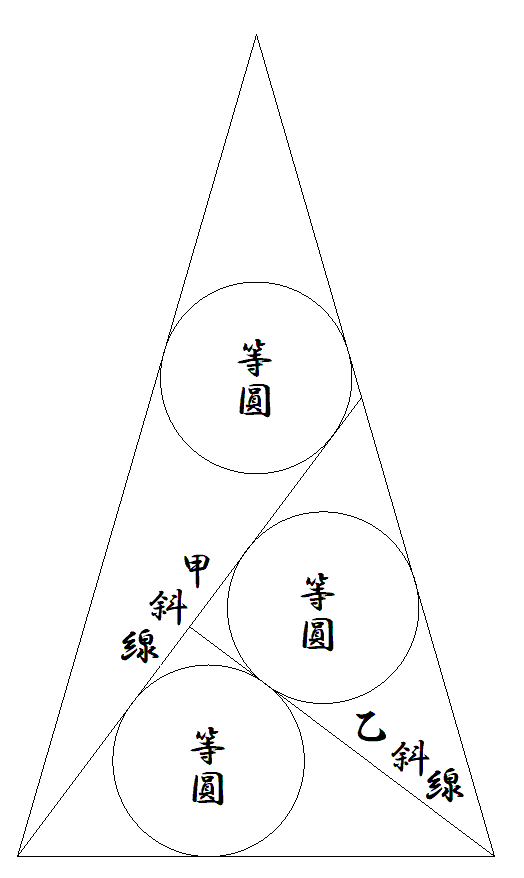 |
|
1辺の長さが1である正三角形ABCのCA上に点Dを, BD上に点Eを,△ABD,△DEC,△EBCの内接円の 半径が等しくなるようにとる。 (1) AD=xとおくとき,xの満たす方程式を求めよ。 (2) 等円の半径をrとおくとき,rの満たす方程式を 求めよ。 | 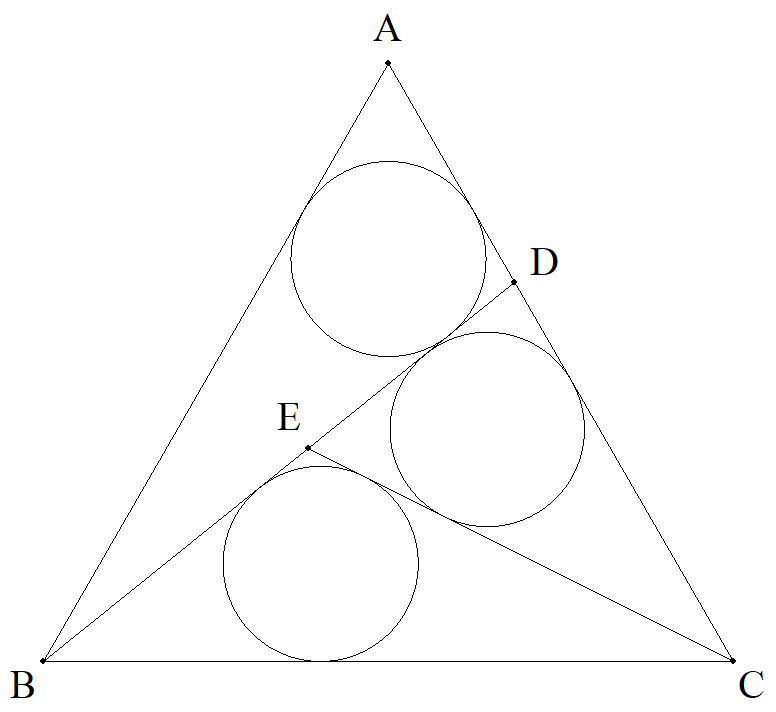 |
|
交わる3個の甲円の間に4個の乙円が図のように接している。 さらに3個の丙円が甲円,乙円に接している。 甲円の半径を知って,乙円,丙円の半径をそれぞれ求めよ。 | 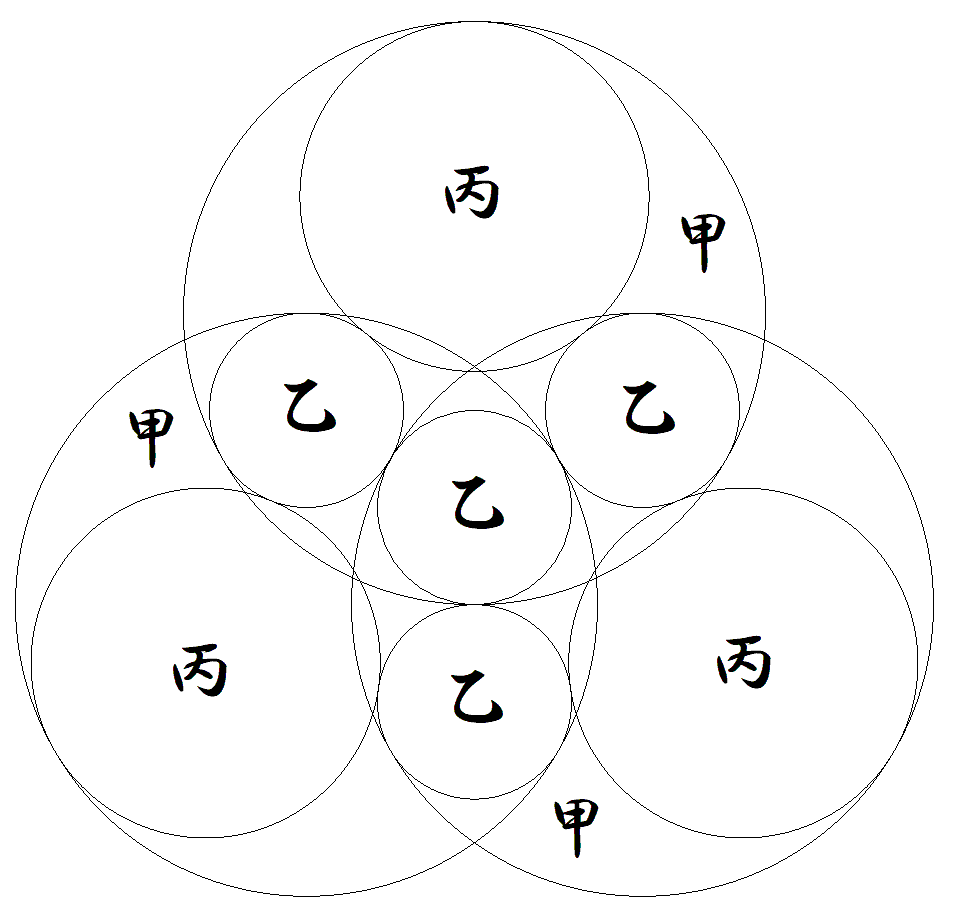 |
|
円に弦を引き緑円と青円を入れる。さらにその隙間に 黄円2個,赤円2個を入れる。 このとき黄径と赤径が等しくなることを証明せよ。 | 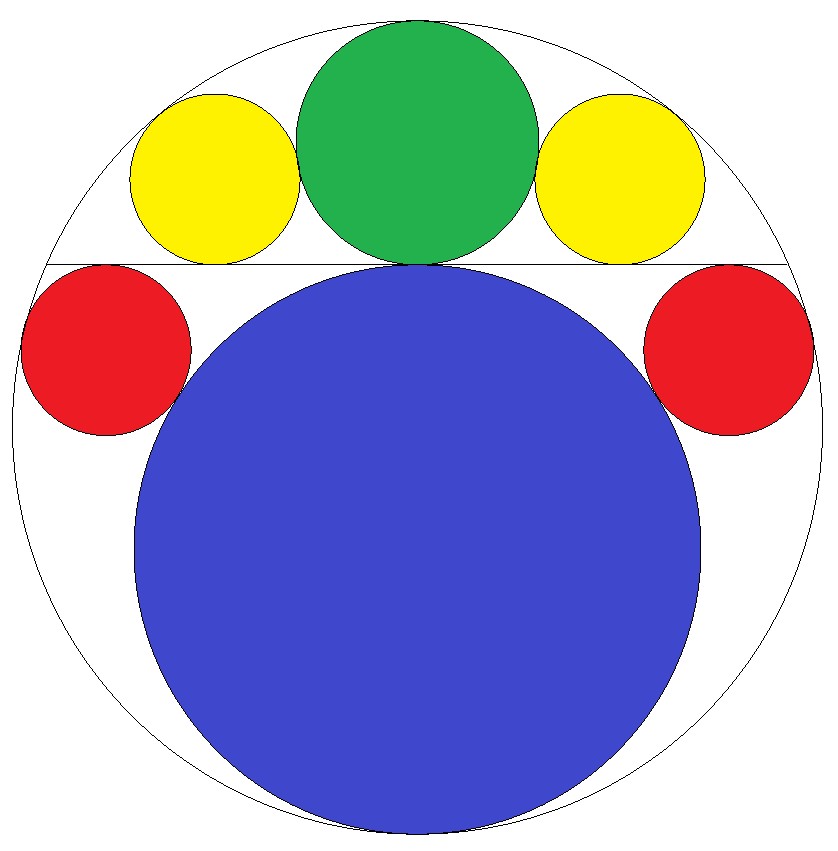 |
|
長方形ABCと中心角90°,半径Rの扇形AOEと 2円O1,O2は,図のように配置されている。 2円O1,O2の半径をそれぞれr1,r2とする。 (1) r1,r2を用いて,Rを求めよ。 (2) R,r2を用いて,r1を求めよ。 (3) R,r1を用いて,r2を求めよ。 | 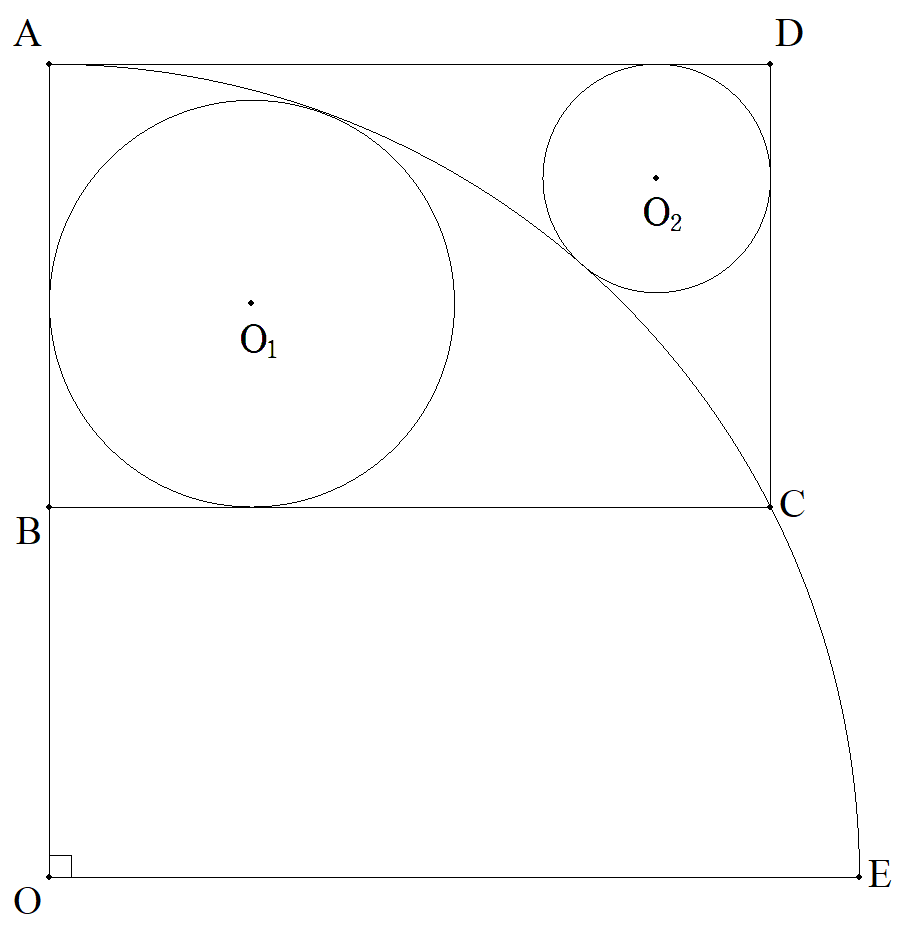 |
|
横の長さが4である長方形内に, 図のように甲円3個,乙円2個, 丙円2個が入っている。 長方形の縦の長さを求めよ。 | 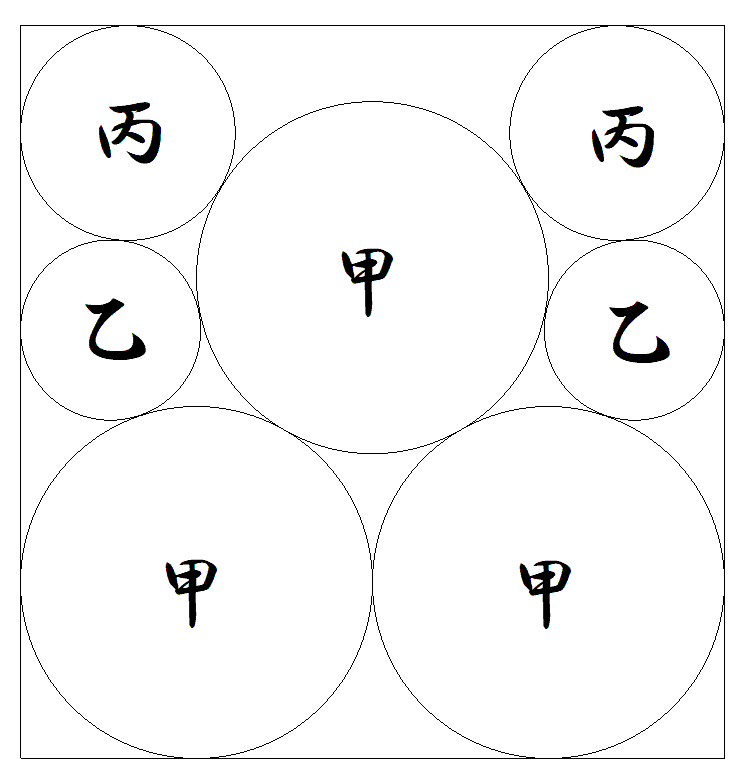 |
|
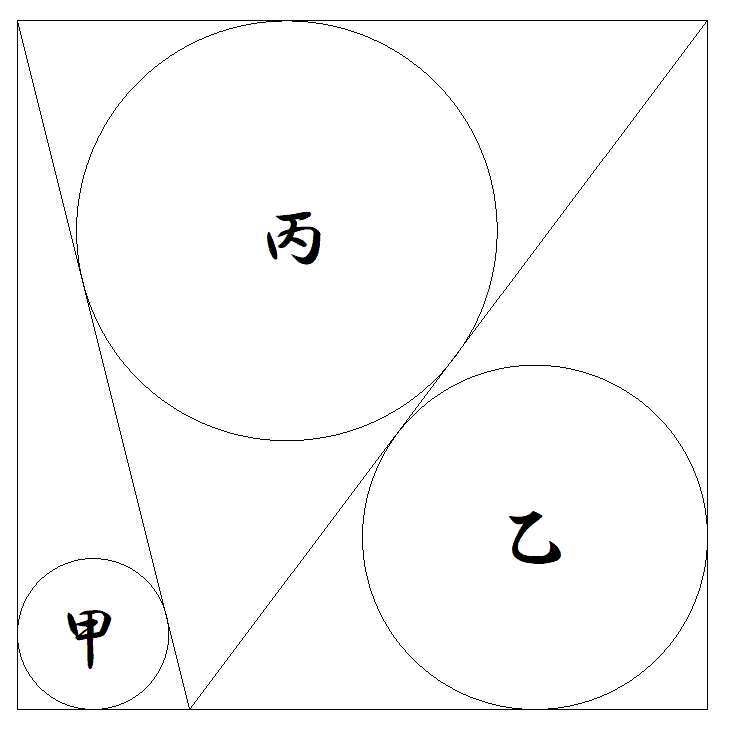
底辺10,等辺13の二等辺三角形に,図のように甲乙丙円が入っている。 甲と丙の半径がそれぞれ2,9/8のとき,乙円の半径を求めよ。 | 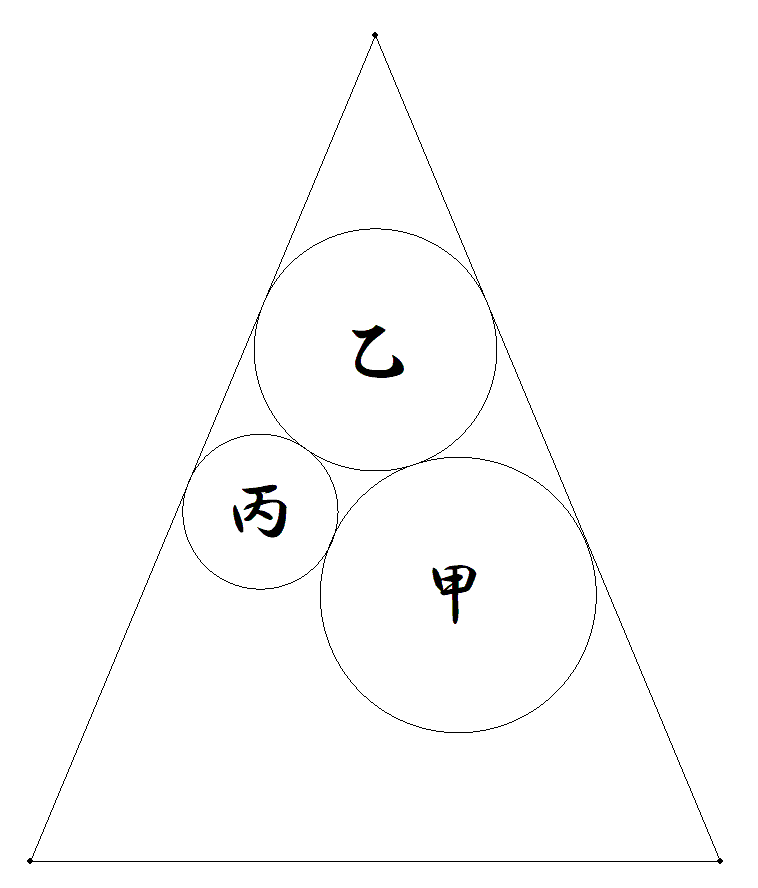 |

|  |
|
底辺10,等辺13の二等辺三角形に,図のように甲乙丙円が 等辺に接するように配置されている。 乙と丙の半径がそれぞれ4,1のとき,甲円の半径を求めよ。 | 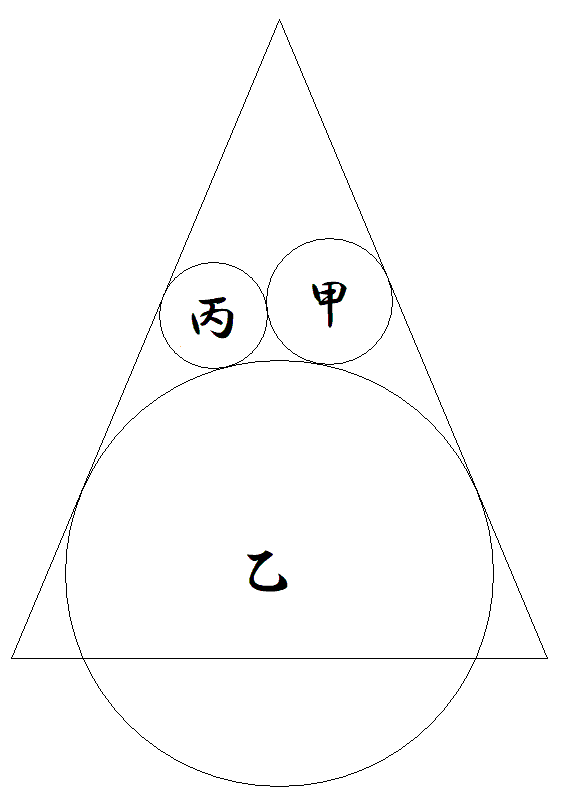 |
|
2つの長方形ABCD,DEFGについて, AはEF上に,GはBC上にあり, ABとFGの交点をHとする。 四角形AHGDの面積をS´,六角形 BCDEFHの面積をSとおくとき, S´/Sのとりうる値の範囲を求めよ。 | 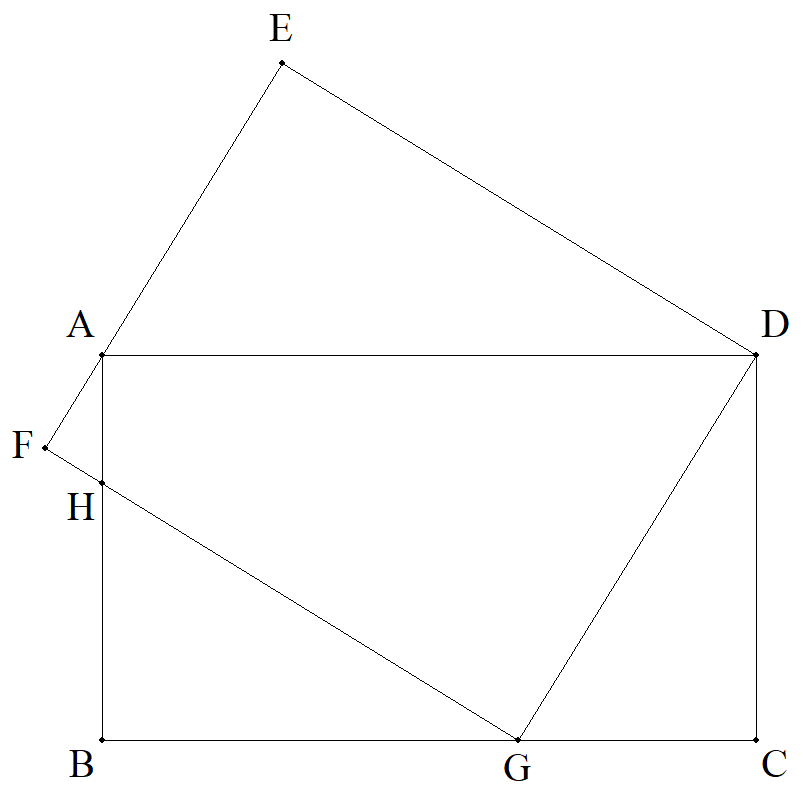 |
|
図のように半径1の四分の一円内に 正方形赤青黄が配置されている。 正方形黄の一辺を求めよ。 | 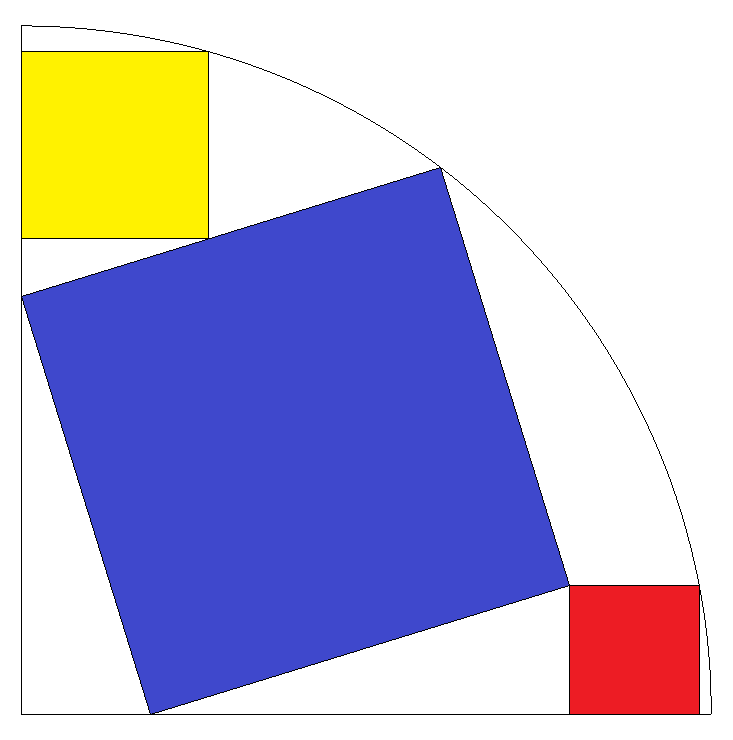 |
|
半径1の四分の一円内に図のように正三角形赤3個と 正三角形青1個が配置されている。 正三角形青の一辺を求めよ。 | 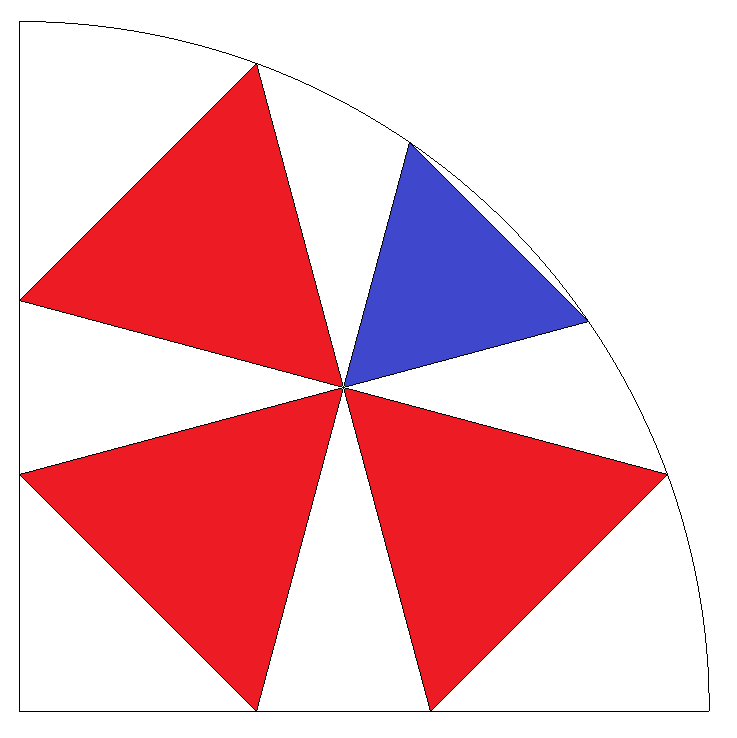 |
|
半径1の四分の一円内に図のように正三角形赤3個と 正三角形青1個が配置されている。 ただし,下側の赤と青の底辺は平行である。 このとき,正三角形青の一辺を求めよ。 | 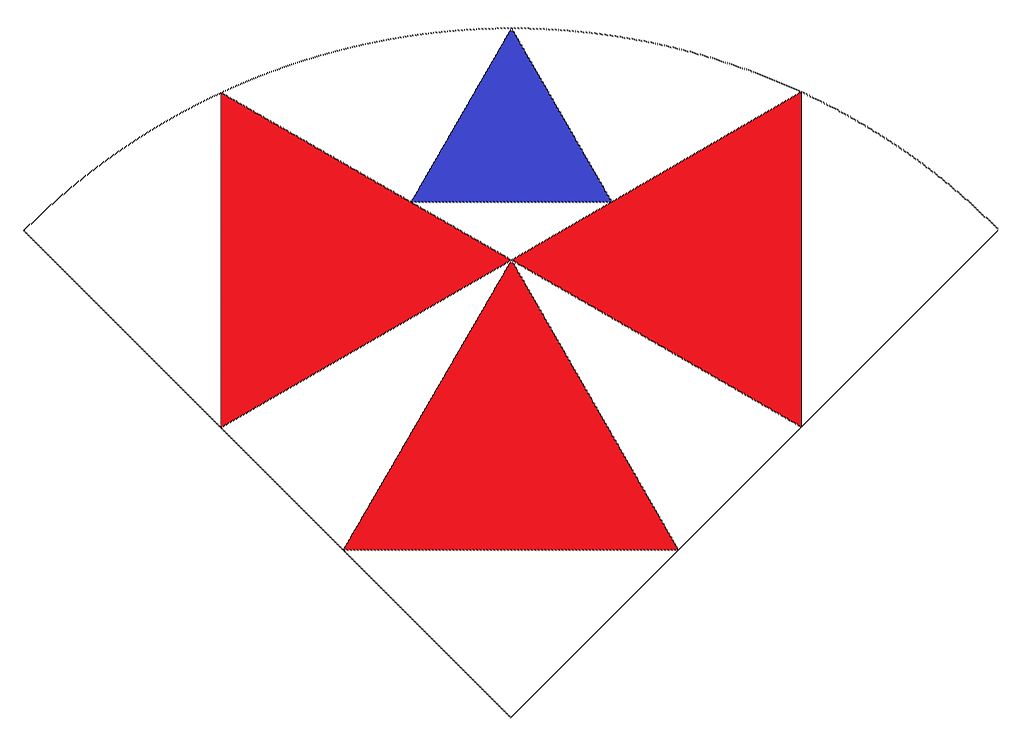 |
|
図のように半径1の半円に甲乙丙丁円が配置されている。 丁円の半径を求めよ。 | 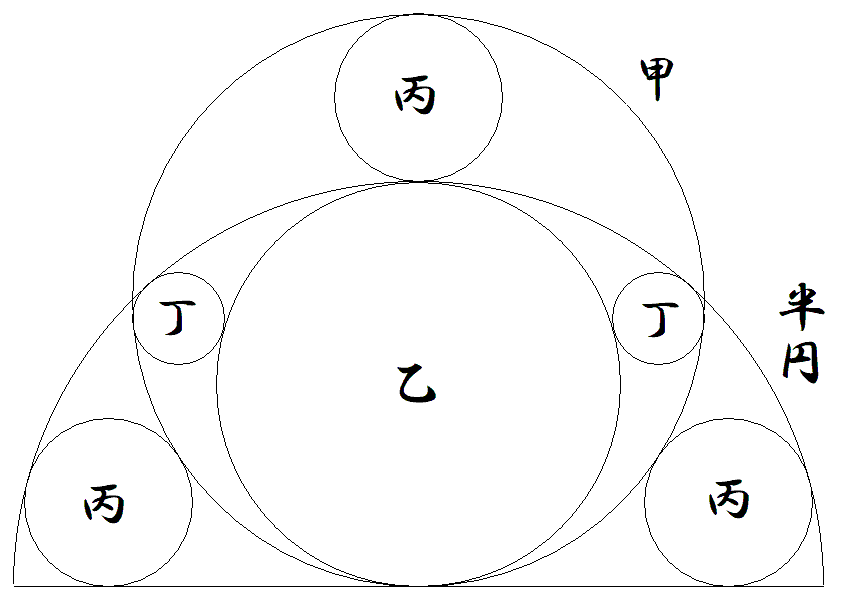 |
|
半径1の半円内に直径1の甲円と円弧乙を入れ,その間に 4個の丙円を入れる。 ただし,半円,甲円,円弧乙の中心は同一直線上にある。 円弧乙,丙円の半径をそれぞれ求めよ。 | 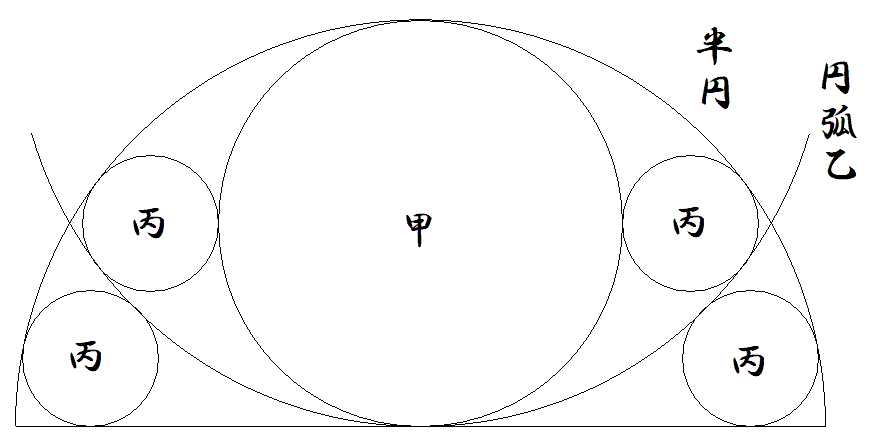 |
|
半径1の半円内に直径1の甲円と円弧を入れ,その間に 6個の乙円を入れる。 ただし,半円,甲円,円弧の中心は同一直線上にある。 乙円の半径rの満たす方程式を一つを求めよ。 | 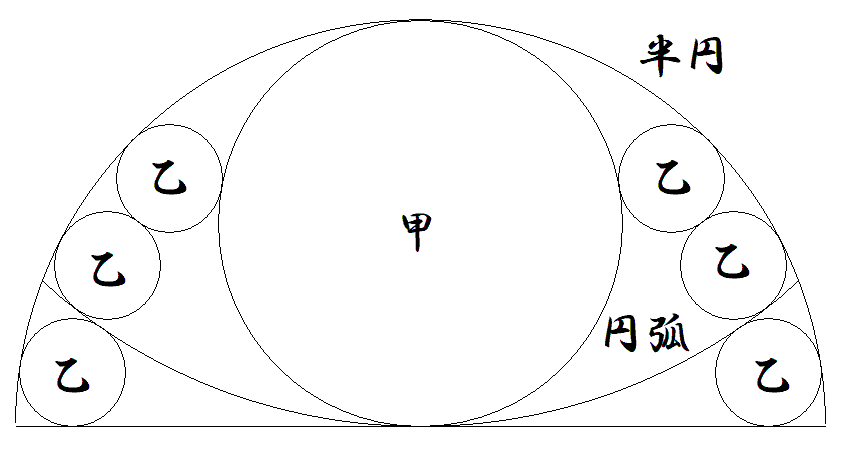 |
ある6桁の数N=a×105+b×104+c×103+d×102+e×10+fをabcdefで表す。
N×2=cdefab,N×3=bcdefa,N×4=efabcd,N×5=fabcde,N×6=defabc
のとき,N×7の値を求めよ。
|
半径1の円に相交わる等しい2つの弦を引き, 小円11個と大円1個を入れる。 小円,大円の半径をそれぞれ求めよ。 | 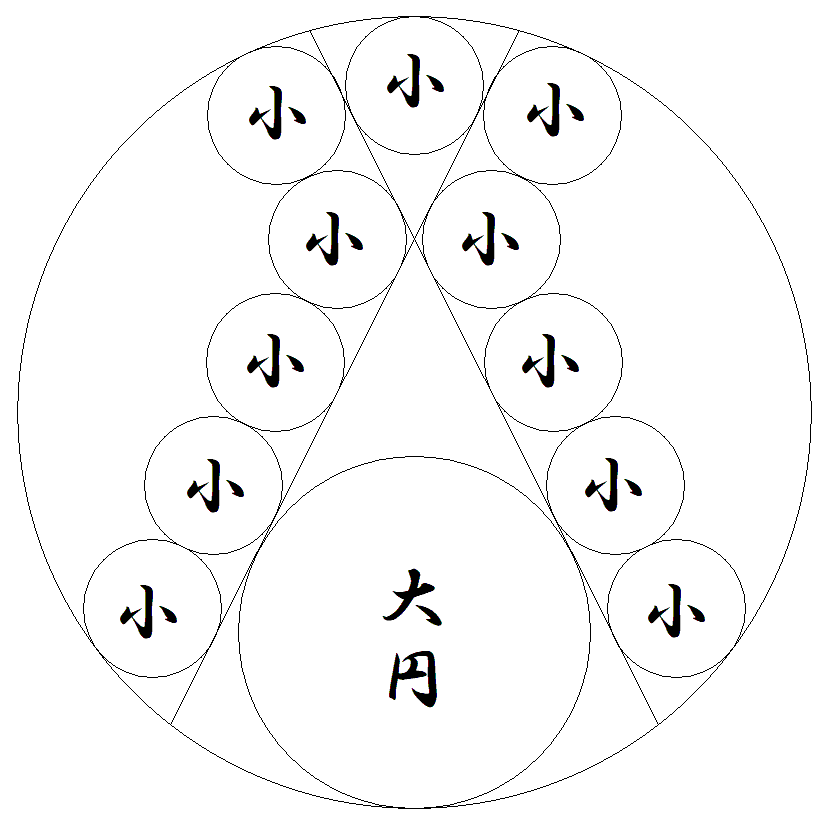 |
|
円に外接する四辺形ABCDの辺BC上に任意の点Eをとる。 △AED,△ABE,△DECの内接円をO1,O2,O3とすると き,2円O2,O3のBCでない共通外接線は円O1に接するこ とを証明せよ。 | 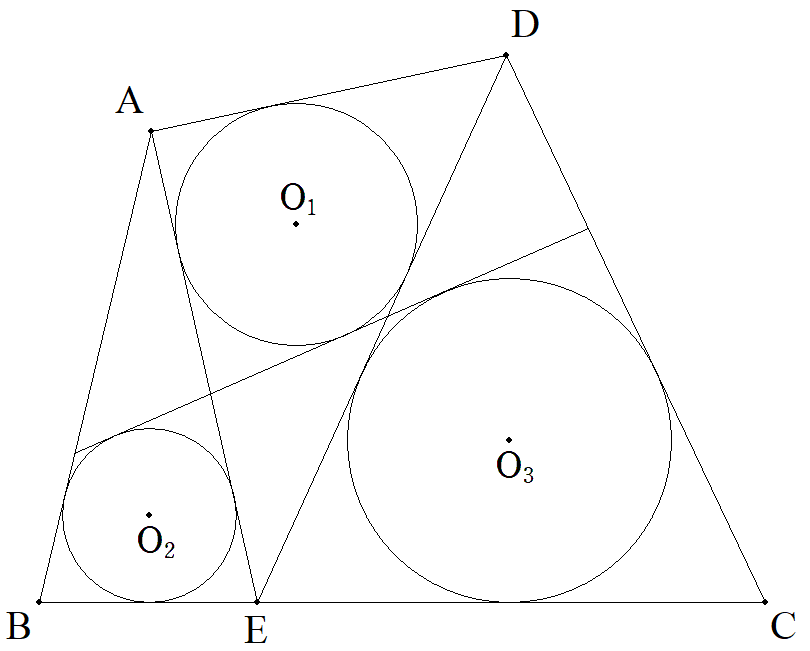 |
(684の逆)
|
四辺形ABCDの辺BC上に任意の点Eをとり,△AED, △ABE,△DECの内接円をO1,O2,O3とする。2円 O2,O3のBCでない共通外接線が円O1に接するとき, 四角形は円に外接することを証明せよ。 |  |
|
1辺の長さが1である正方形内に図のように 甲円1個,乙円2個,丙円1個が配置されて いる。 甲乙丙円の半径をそれぞれ求めよ。 |  |
|
1辺の長さが1である正方形と甲円が図のよう に配置されている。 乙円は正方形の2辺を延長した線分と甲円に接し, 丙円は甲乙円と正方形に接する。 このとき,甲乙丙円の半径をそれぞれ求めよ。 | 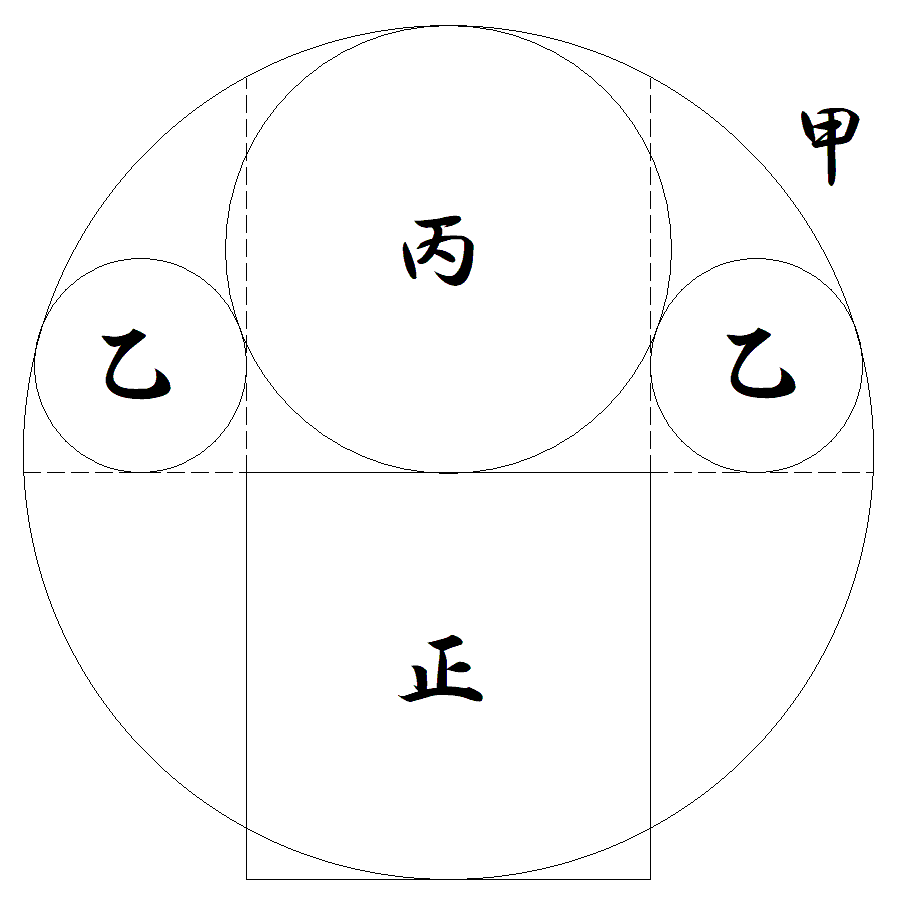 |
|
1辺の長さが1である正方形と甲円が図のよう に配置されている。 乙円は正方形の2辺を延長した線分と甲円に接し, 丙円は甲乙円と正方形に接する。 このとき,甲乙丙円の半径をそれぞれ求めよ。 | 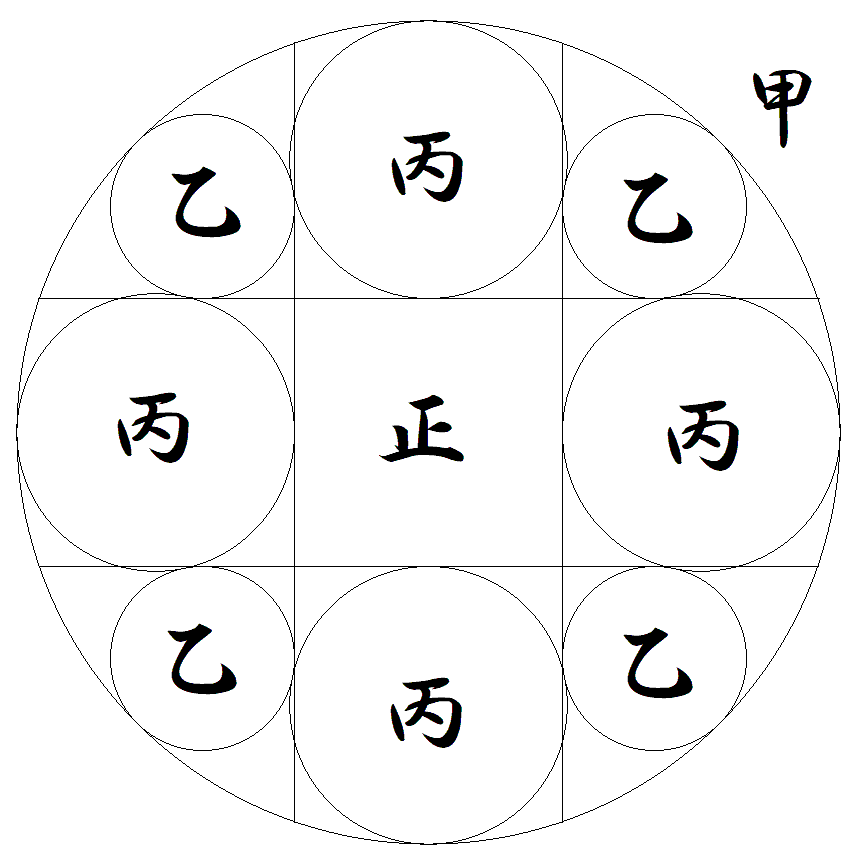 |
|
正方形甲内に図のように正方形乙丙丁 戊が配置されている。 図のa,bの長さが与えられたとき, 正方形丙丁戊の1辺の長さをそれぞれ 求めよ。 | 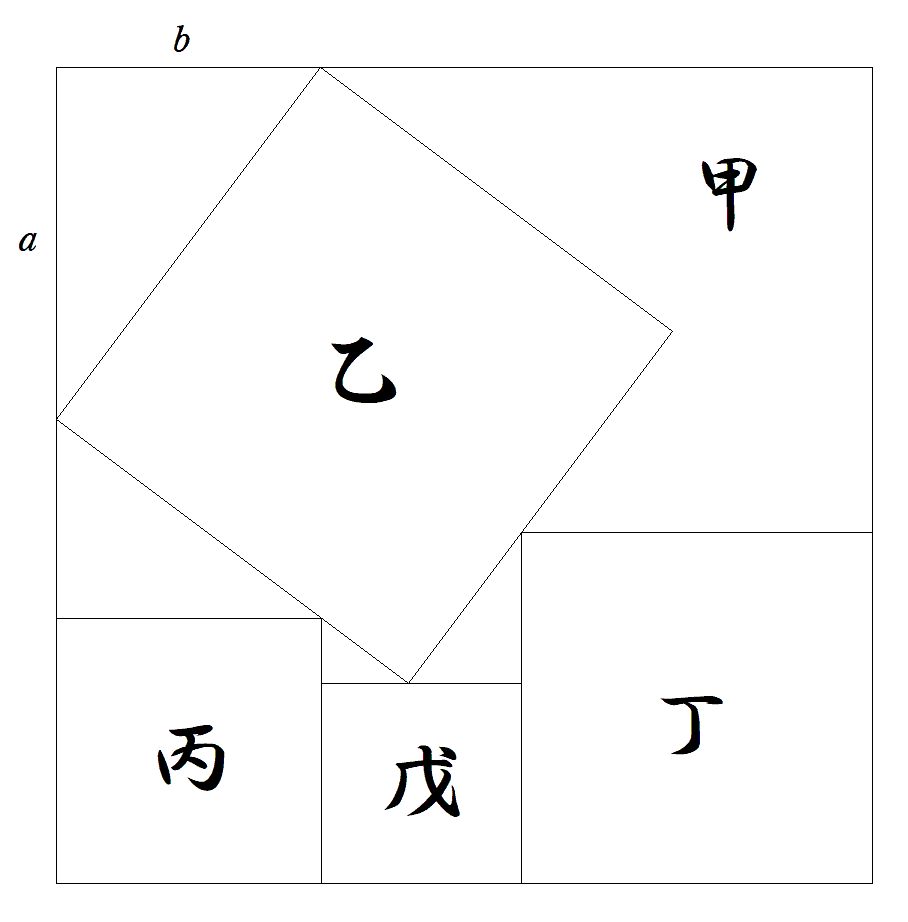 |
|
正方形内に図のように正方形赤青黄緑が配置さ れている。 正方形青黄緑の1辺の長さをそれぞれx,y,zと おくとき,正方形赤の1辺を求めよ。 |  |
|
1辺の長さが1である正方形内に, 図のように4個の正三角形甲乙丙 丁が配置されている。 それぞれの1辺を求めよ。 | 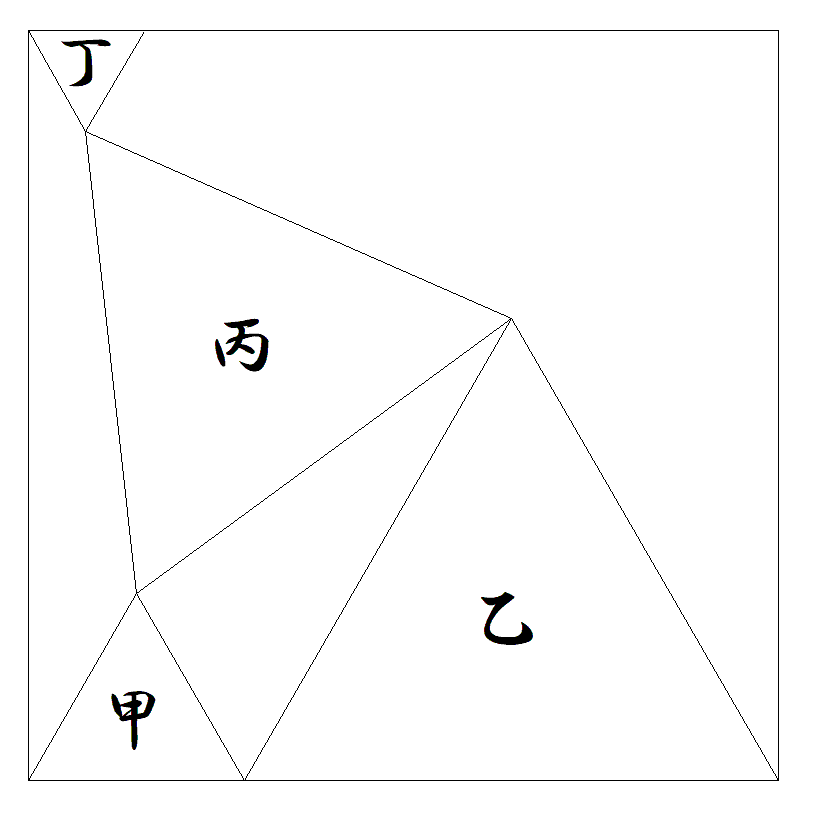 |
|
図のように,正方形内に 4個の正三角形赤青黄緑 が配置されている。 黄の面積が1のとき正方形 の面積を求めよ。 | 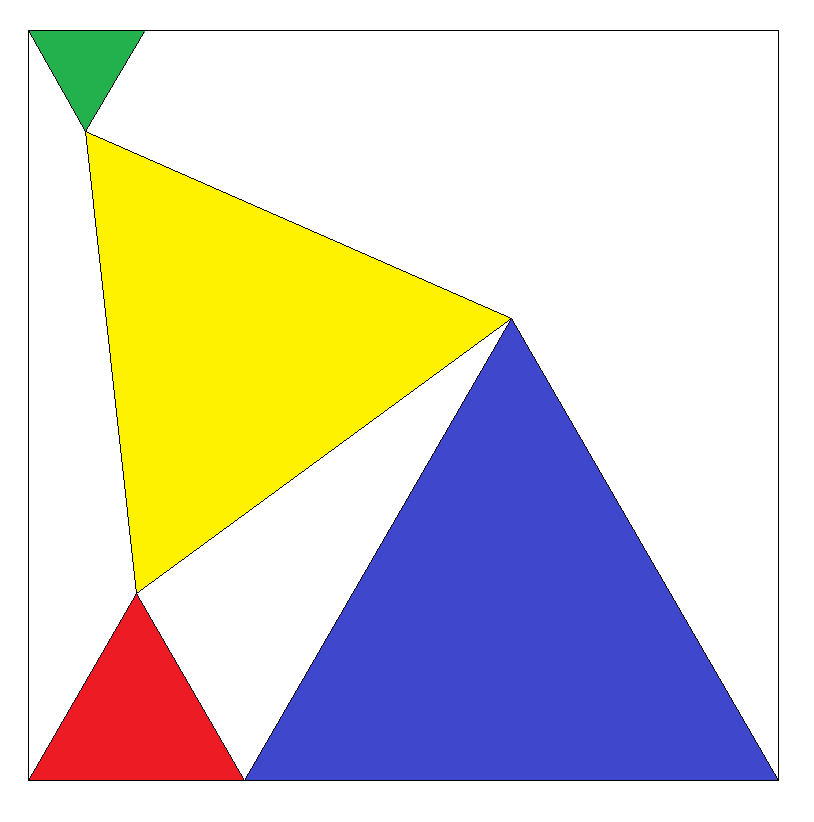 |
|
半円O(R)内に2円O1(r1)とO2(r2)と半円O3(r3)が 図のように入っている。 2円の共通外接線の長さがaのとき, (1) r3をa,r1,r2を用いて表せ。 (2) Rをa,r1,r2を用いて表せ。 (3) r1,r2,r3,Rの関係式を求めよ。 | 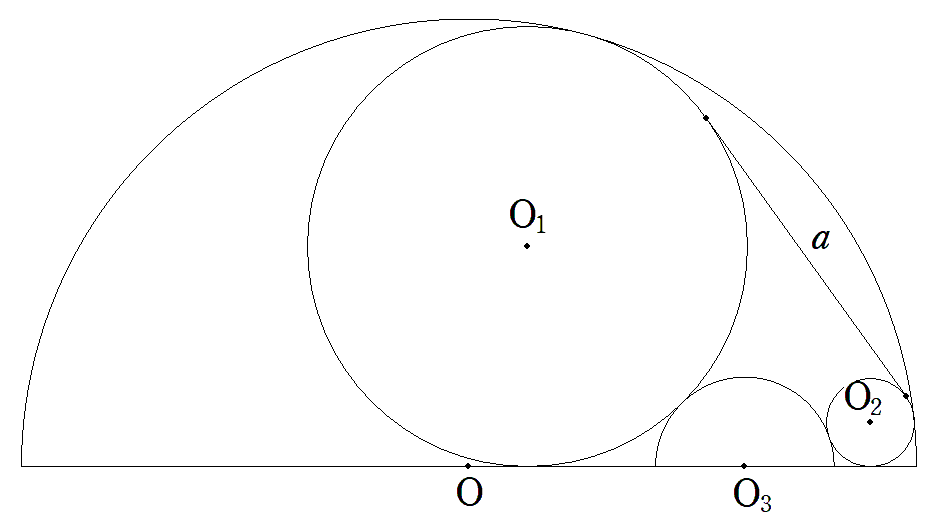 |
|
半径rの半円内に半径5の円と半径1の円と半径r/5の半円が 図のように入っている。 このとき,2円の共通外接線の長さaを求めよ。 | 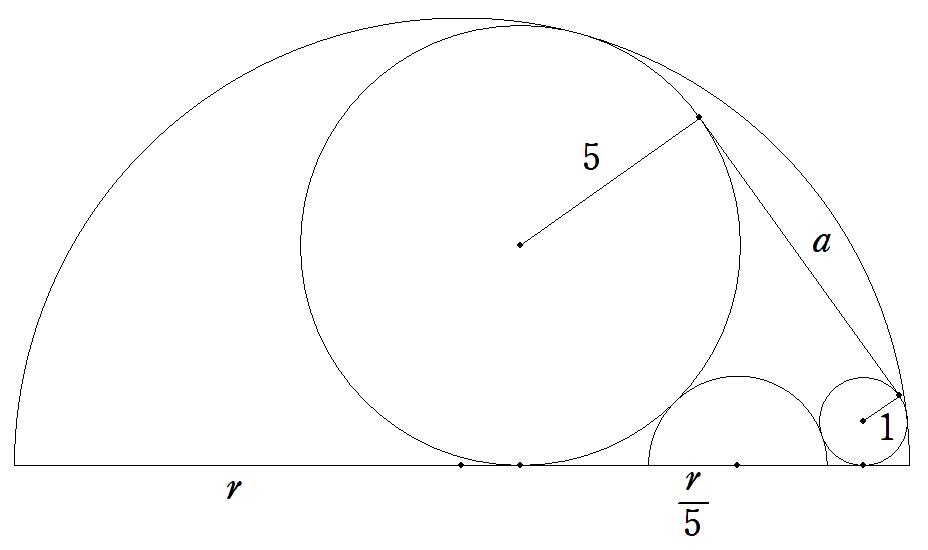 |
|
大円内に甲円2個,乙円1個,丙円2個が 図のように入っている。 甲乙丙円の半径がそれぞれ7,4,2のとき, 大円の半径を求めよ。 | 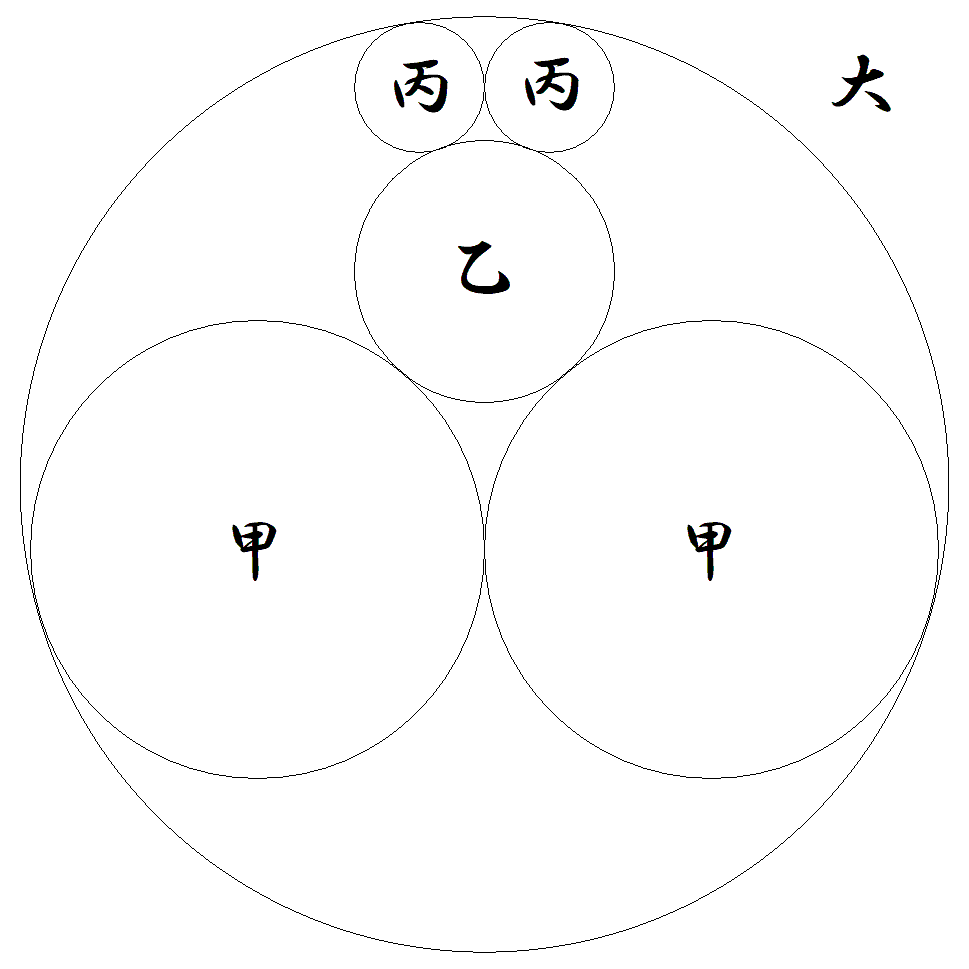 |
|
図のように4円O1(r1),O2(r2),O3(r3),O4(r4)は それぞれ長方形の直角を挟む2辺に接し,円O1は 他の3円に接する最大円である。このとき, (1) r4をr1,r2,r3を用いて表せ。 (2) さらに,2円O3,O4が接するとき,√r3,√r4 をそれぞれr1,r2を用いて表せ。 | 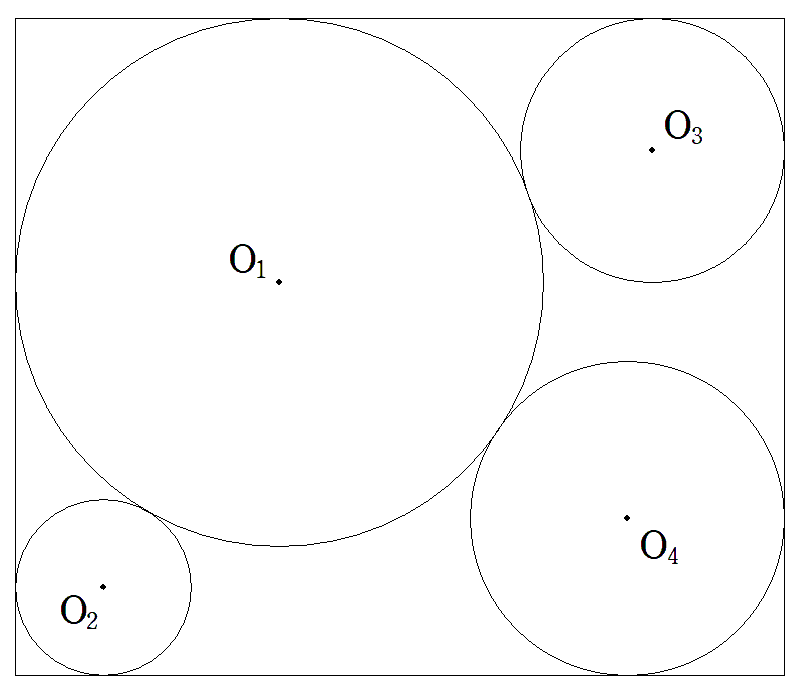 |
|
長方形内に2個ずつの甲乙丙丁円と1個の戊円が 図のように入っている。 甲乙円の半径がそれぞれ4,2のとき,丙丁戊円 の半径をそれぞれ求めよ。 | 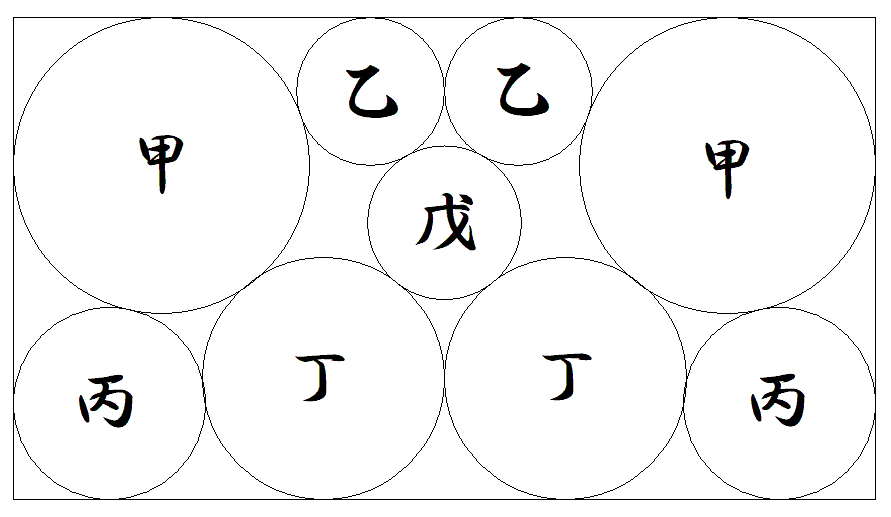 |
|
1辺の長さが1である正方形の辺の中点で甲円,甲´円が接して, 図のように配置されている。 乙円は正方形の延長した2辺と甲円に接し,丙円は甲乙円と正方形 に接する。 乙´円は正方形の2辺と甲´円に接し,丙´円は甲´乙´円と正方形に 接する。 このとき,乙´円径を乙円径を用いて表せ。 | 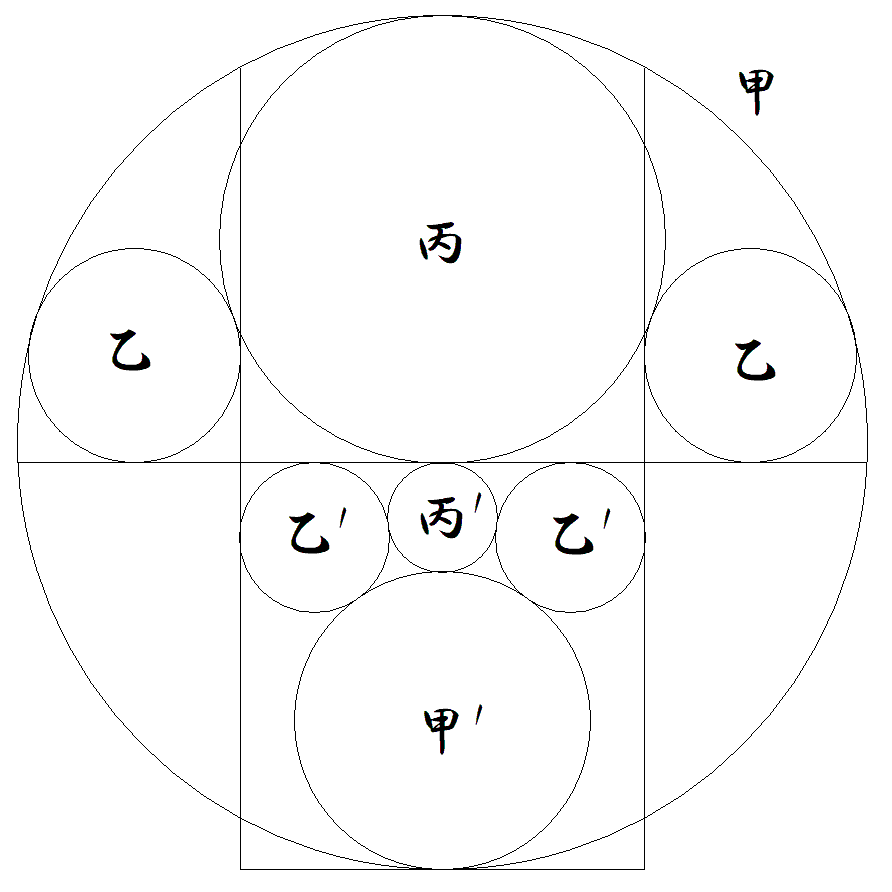 |
|
1辺の長さがaであるの正方形内に2個ずつ 1辺の長さがbである正方形,甲円,乙円が 図のように入っている。 甲乙円の半径をそれぞれa,bを用いて表せ。 | 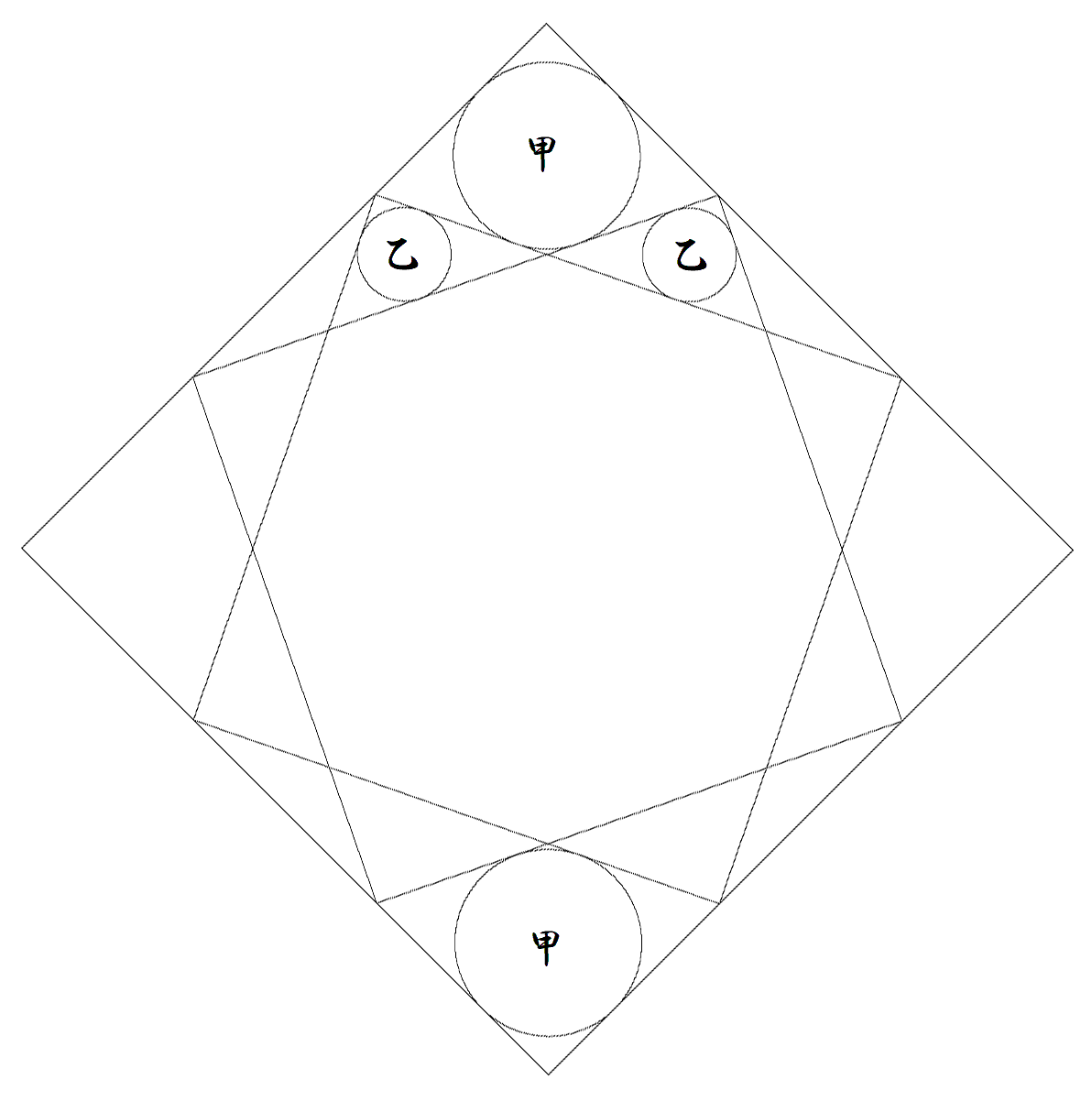 |
|
正n角形内に1個の正n角形が内接し, その隙間にn個の等円が内接している。 n個の等円の中心を頂点とする正n角形 と内接正n角形は合同になることを証明 せよ。(図はn=5の場合) | 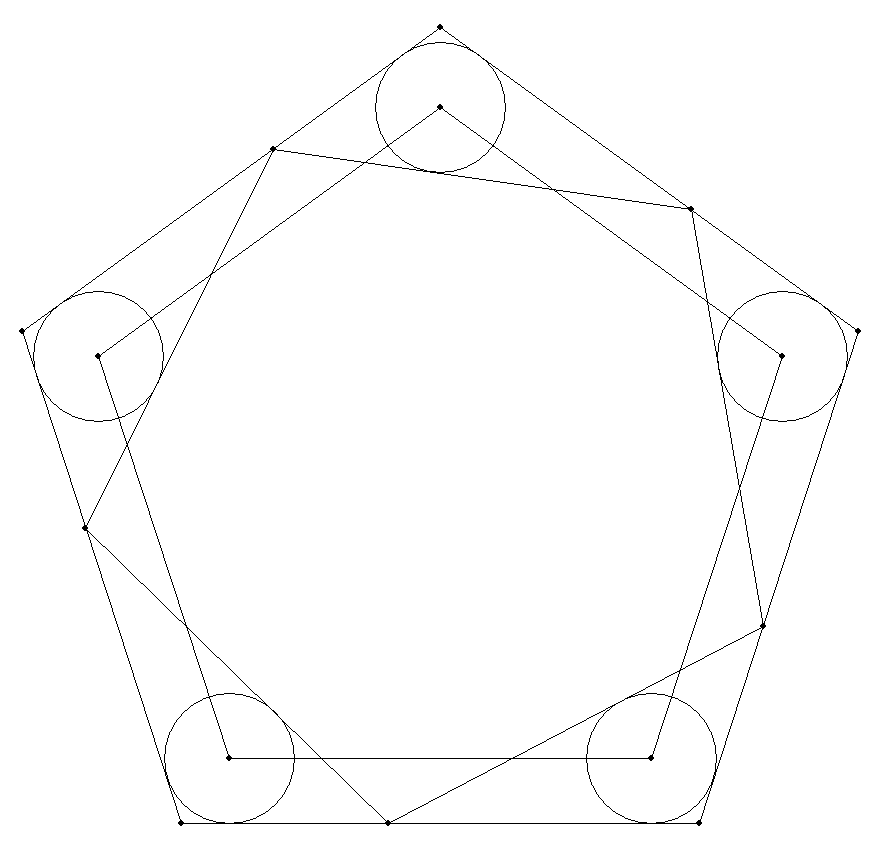 |