■趣味の数学問題集・Ａ問題







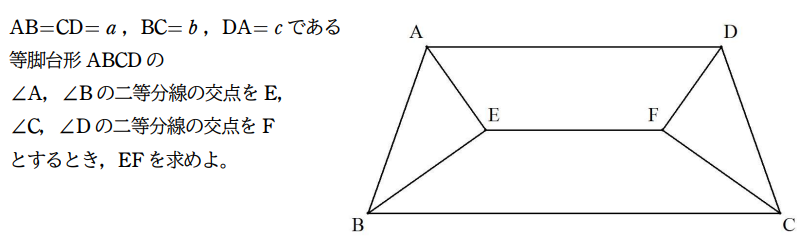
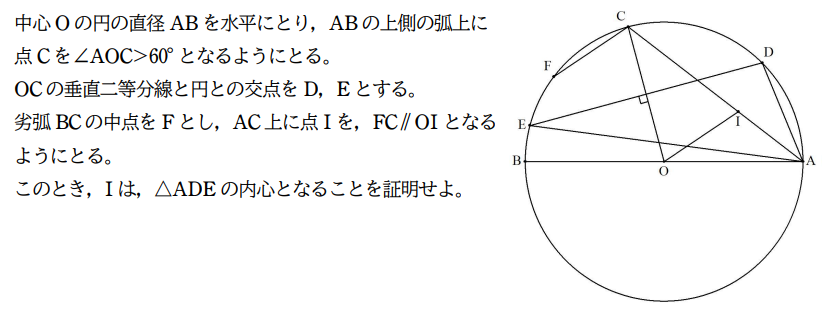
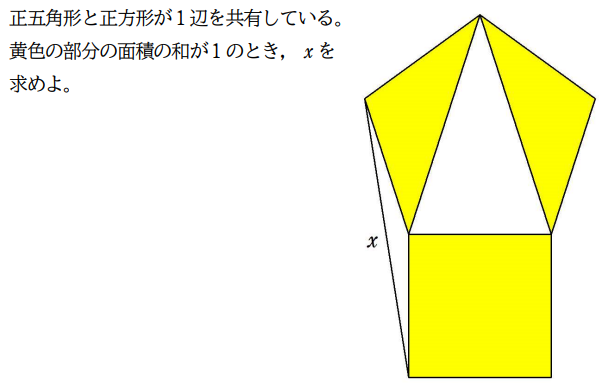
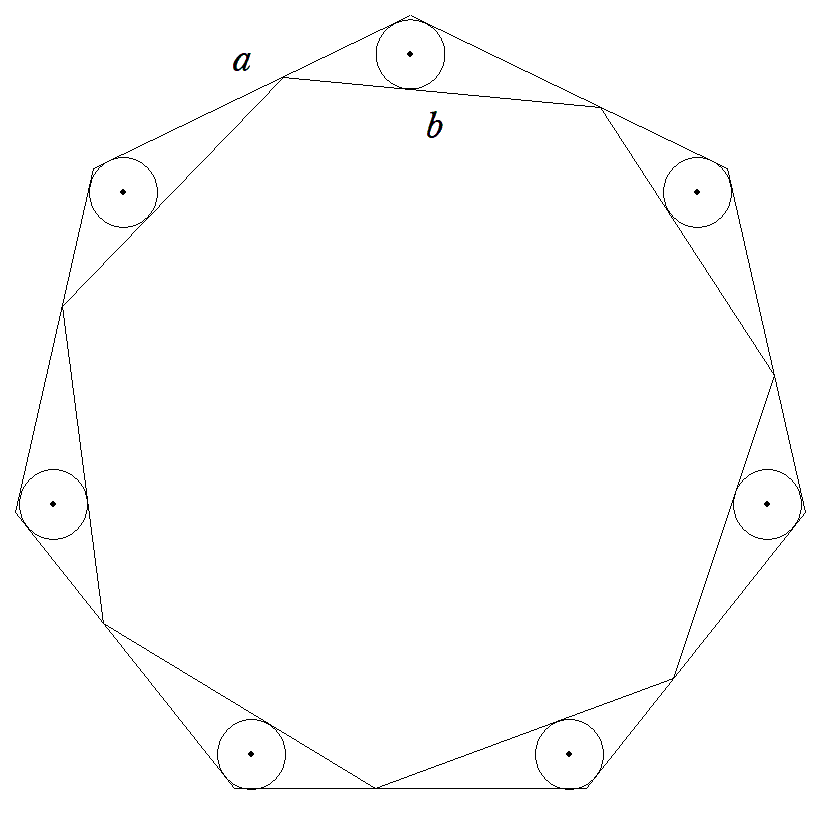  3. △ABCで，AB＝BC，AD∥EFのとき，AC＝xを求めよ。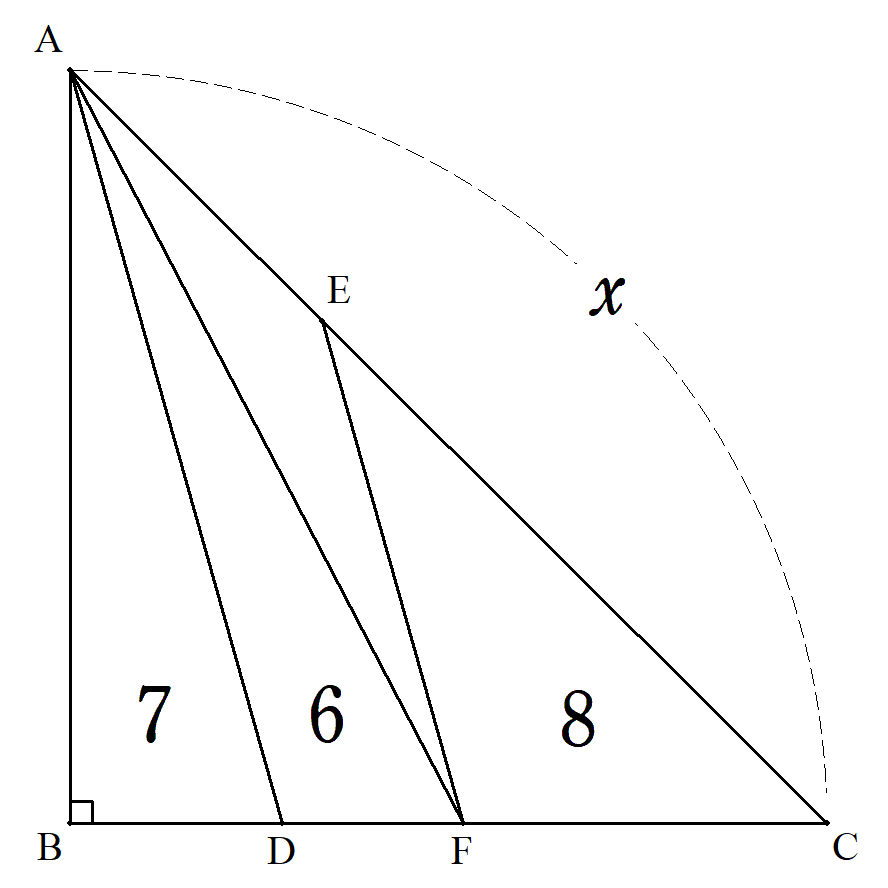



  4. 正方形ABCDのAB，BCの中点を
    それぞれE，Fとする。
    正方形内に点Gを△EFGが正三
    角形になるようにとる。
    DA上に点Hを∠GEH＝60°となる
    ようにとる。
    HからEGに下した垂線の足をIとす
    る。
    このとき，次を示せ。
    (1)　HI=IG=GD
    (2)　△HEG＝2△GFD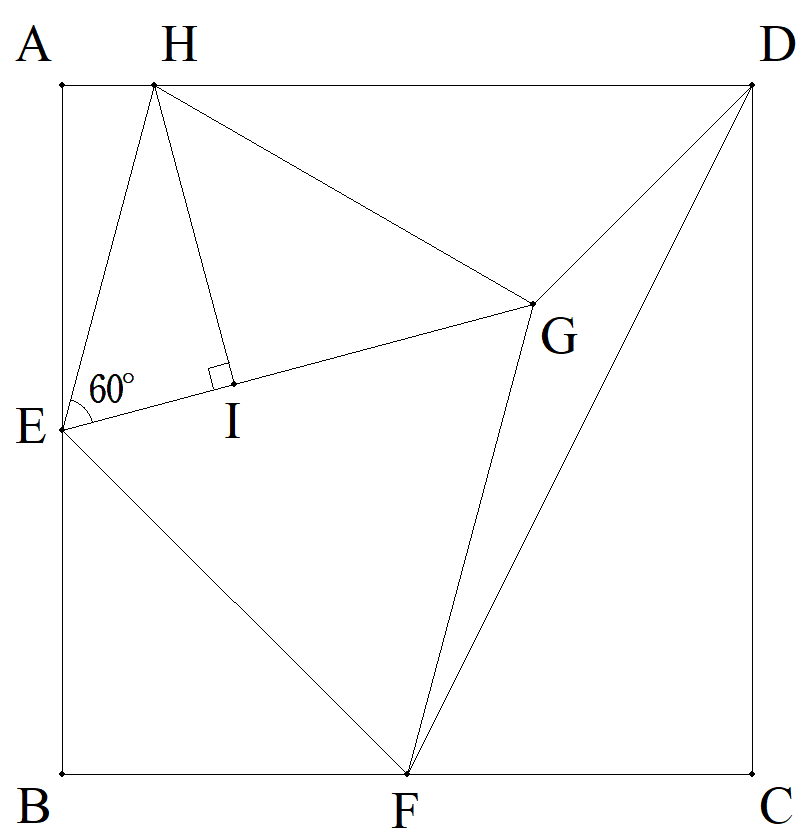



  5. △ABCの外心をOとする。
    ∠OAB＋∠OBC＋∠OCA＝90°のとき，三角形の形状を考察せよ。


  6. △ABCにおいて，AC，ABの中点をそれぞれM2，M3，
    B，CからCA，ABに下した垂線の足をそれぞれH2，H3
    とする。
    H2M2＝H3M3のとき，三角形の形状を考察せよ。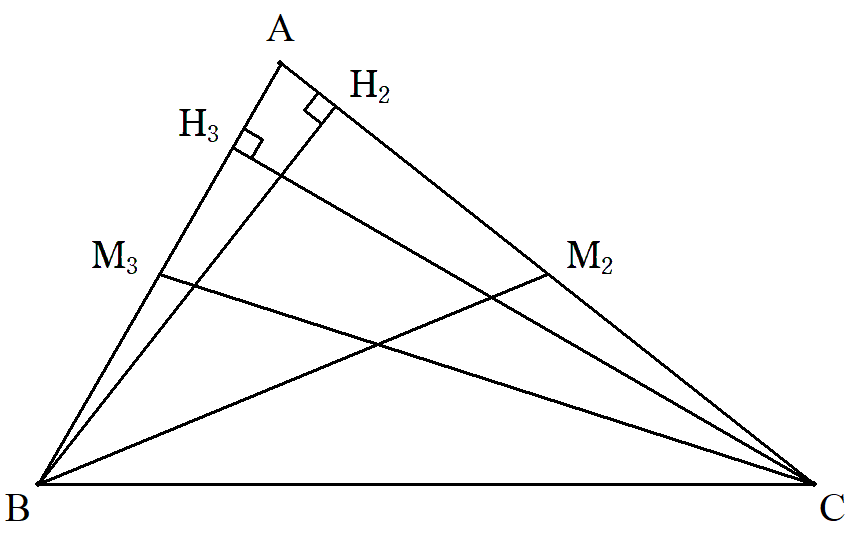



  7. 3個の半径1の等円の中心は同一直線上にあり，
    その隙間に，赤青黄円を図のように配置する。
    赤青黄円の半径をそれぞれ求めよ。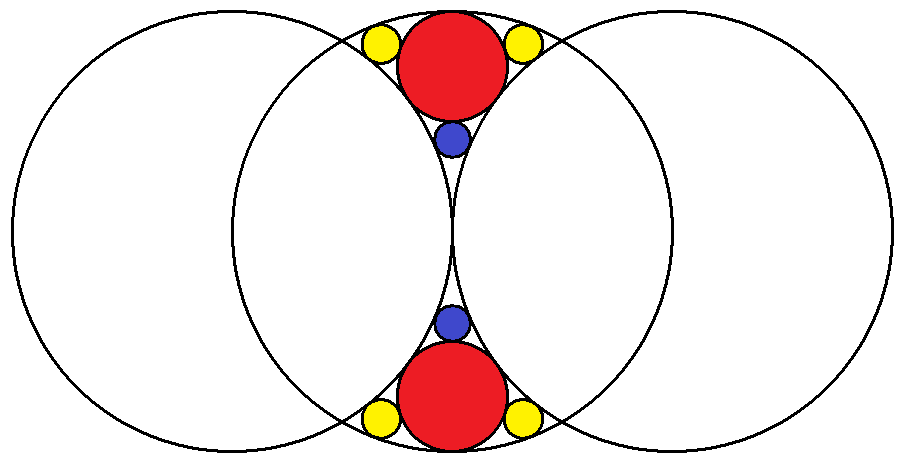



  8. AD∥BC，AB＝CD＝1，BC＝2である等脚台形ABCD内に
    Bを中心，半径1の円弧，Cを中心，半径1の円弧を描く。
    その円弧に接する赤青黄円を図のように配置する。
    (1)　∠ABC＝∠DCB＝θのとき，赤青黄円の半径をそれ
    　　 ぞれ求めよ。
    (2)　(1)でθ＝60°のとき，赤青黄円の半径をそれぞれ
    　　 求めよ。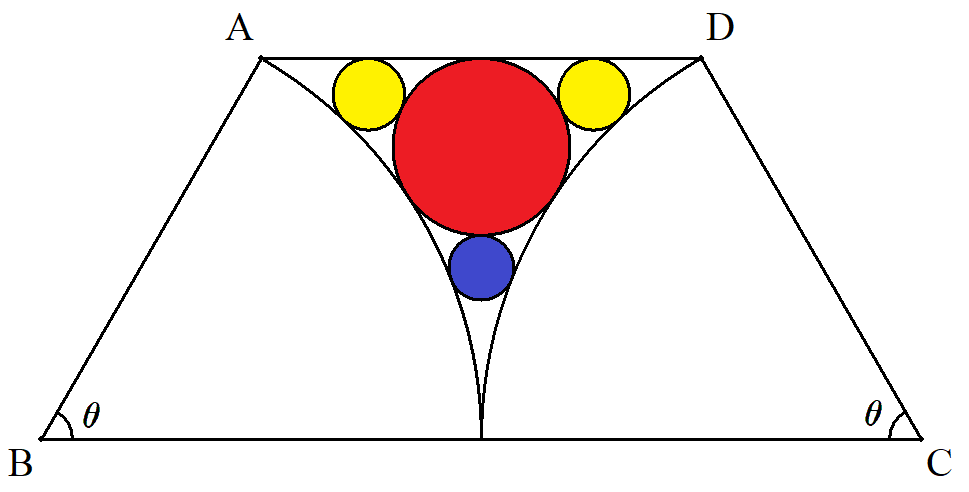



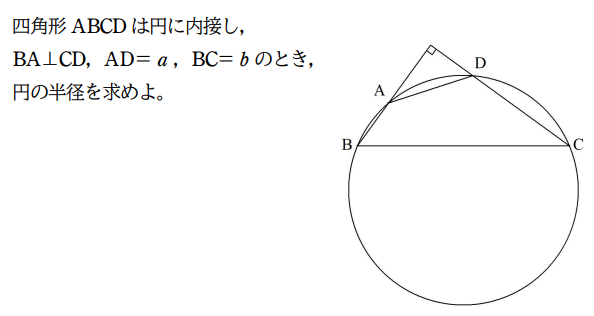
  9. 右図でBDの長さを求めよ。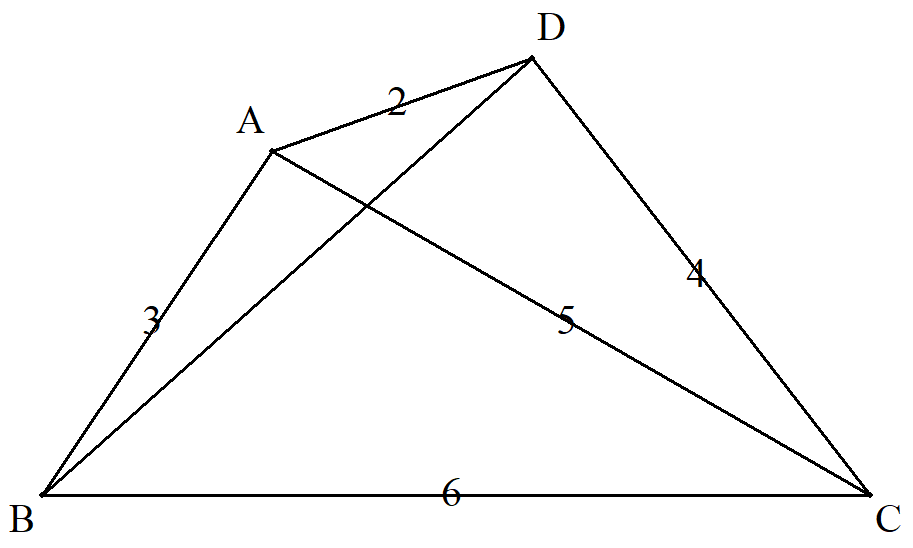



  10. AB＝a，BC＝b，CD＝c，DA＝dである四角形ABCDについて，
    AC＝eのとき，BDを求めよ。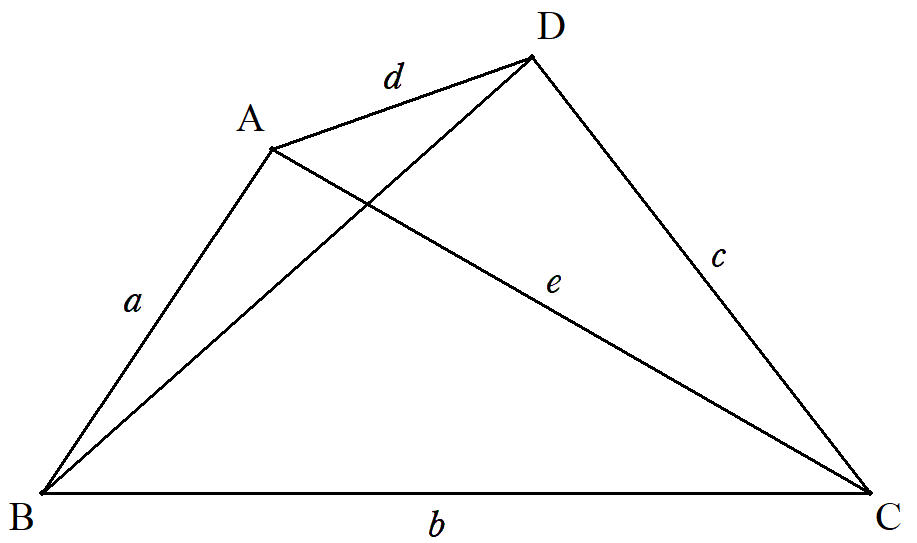



  11. AB＝a，BC＝b，CD＝c，DA＝dである四角形ABCDについて，AC＝e，BD＝fのとき，
    e2f2＝a2c2＋b2d2－2abcd cos(A＋C)を示せ。（Bretschneider）


  12. A，B，Cは1辺の長さが1の正三角形の頂点である。
    この図形の中に図のように互いに接する甲乙円を配置
    する。
    甲乙円の半径をそれぞれ求めよ。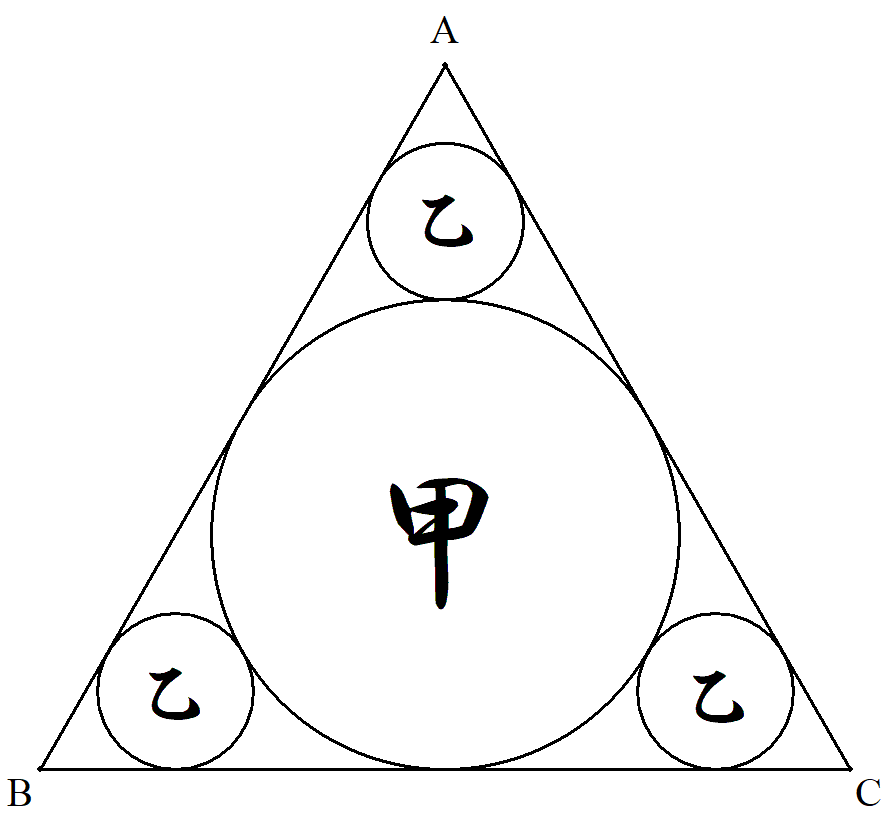



  13. A，B，Cは1辺の長さが1の正三角形の頂点で，
    弧BC，CA，ABは半径1の円弧である。
    この図形の中に図のように互いに接する甲乙円
    を配置する。
    甲乙円の半径をそれぞれ求めよ。



  14. A，B，Cは1辺の長さが1の正三角形の頂点で，
    弧BC，CA，ABは半径1の円弧である。
    この図形の中に図のように互いに接する甲乙円
    を配置する。
    甲乙円の半径をそれぞれ求めよ。



  15. A，B，Cは1辺の長さが1の正三角形の頂点で，
    弧BCは半径1の円弧である。
    この図形の中に図のように互いに接する甲乙丙
    円を配置する。
    甲乙丙円の半径をそれぞれ求めよ。



  16. A，B，Cは1辺の長さが1の正三角形の頂点で，
    弧BCは半径1の円弧である。
    この図形の中に図のように互いに接する甲乙丙
    円を配置する。
    甲乙丙円の半径をそれぞれ求めよ。



  17. A，B，Cは1辺の長さが1の正三角形の頂点で，
    弧CA，ABは半径1の円弧である。
    この図形の中に図のように互いに接する甲乙丙
    円を配置する。
    甲乙丙円の半径をそれぞれ求めよ。



  18. A，B，Cは1辺の長さが1の正三角形の頂点で，
    弧CA，ABは半径1の円弧である。
    この図形の中に図のように互いに接する甲乙丙
    円を配置する。
    甲乙丙円の半径をそれぞれ求めよ。



  19. A，B，Cは1辺の長さが1の正三角形の頂点で，
    弧BC，CA，ABは半径1の円弧である。
    この図形の中に図のように互いに接する甲乙丙
    円を配置する。
    甲乙丙円の半径をそれぞれ求めよ。



  20. A，B，Cは1辺の長さが1の正三角形の頂点で，
    弧BC，CA，ABは半径1の円弧である。
    この図形の中に図のように互いに接する甲乙丙
    円を配置する。
    甲乙丙円の半径をそれぞれ求めよ。



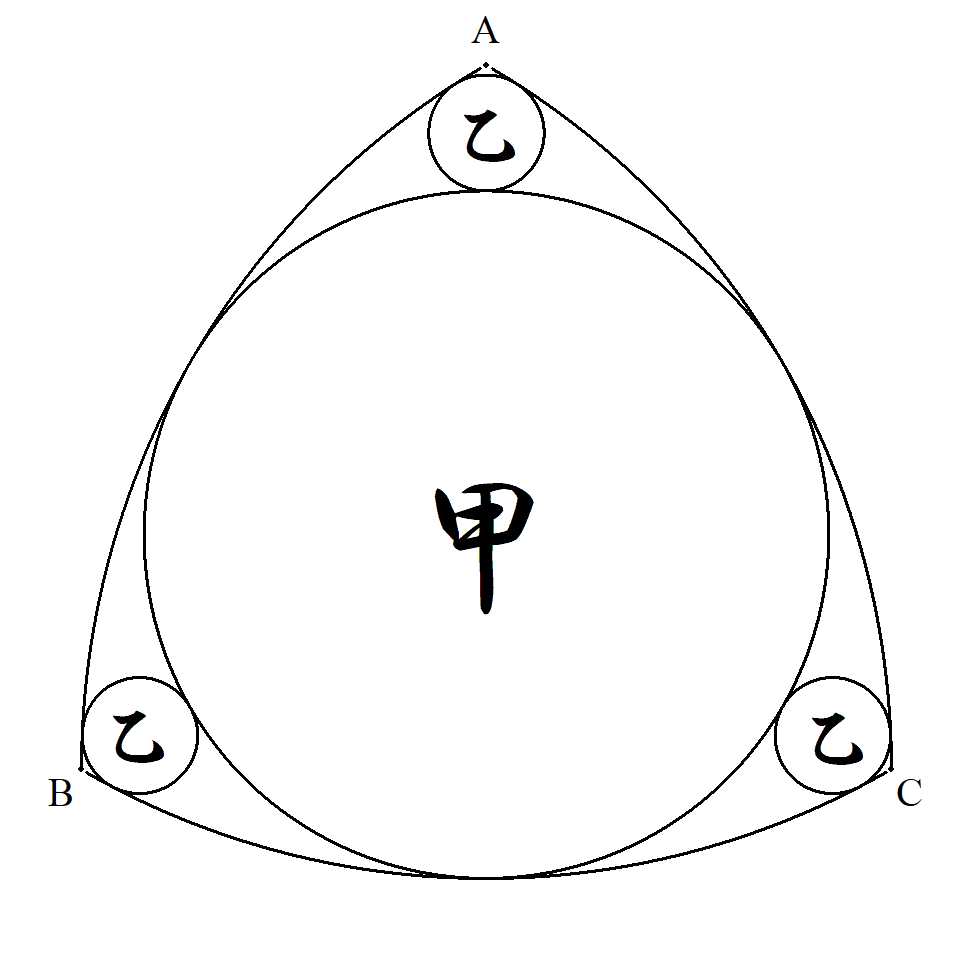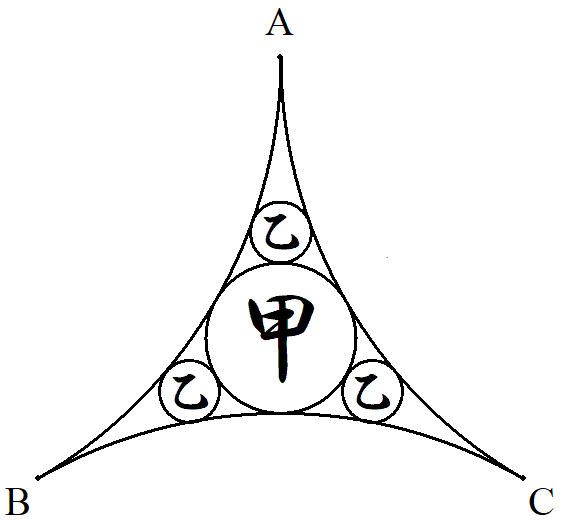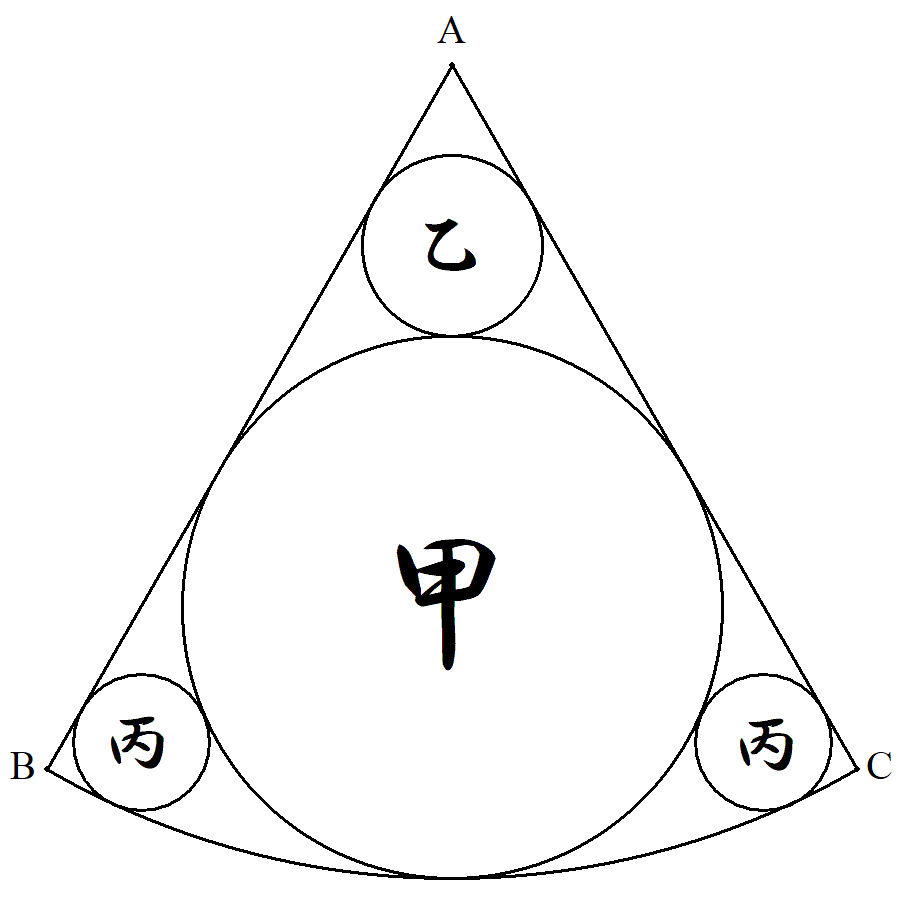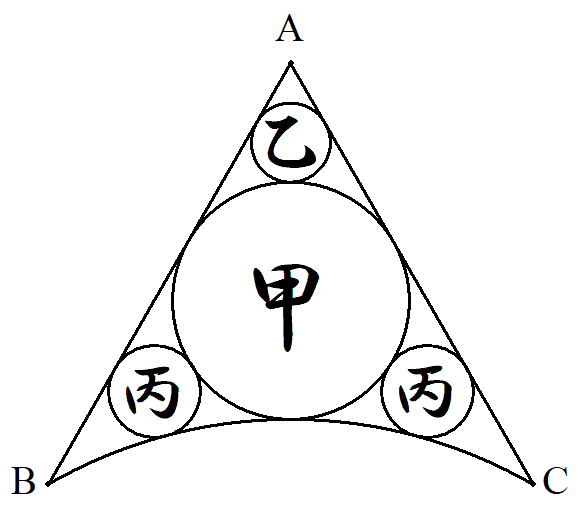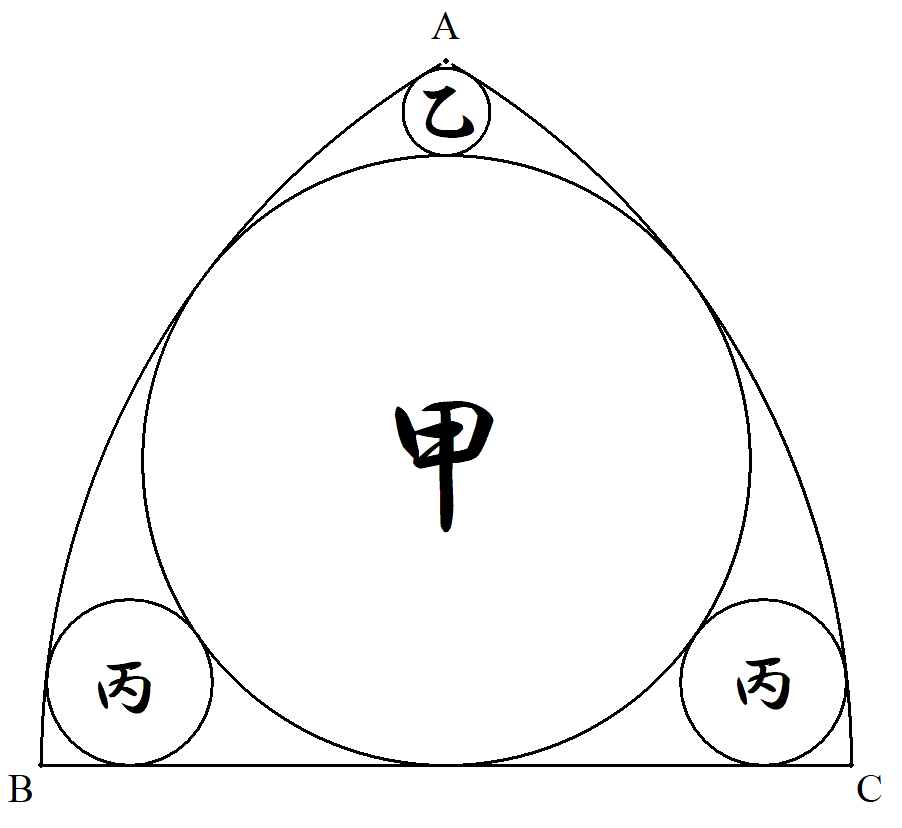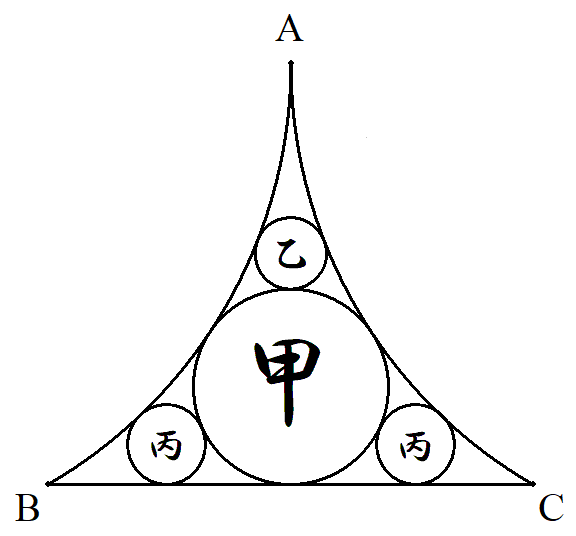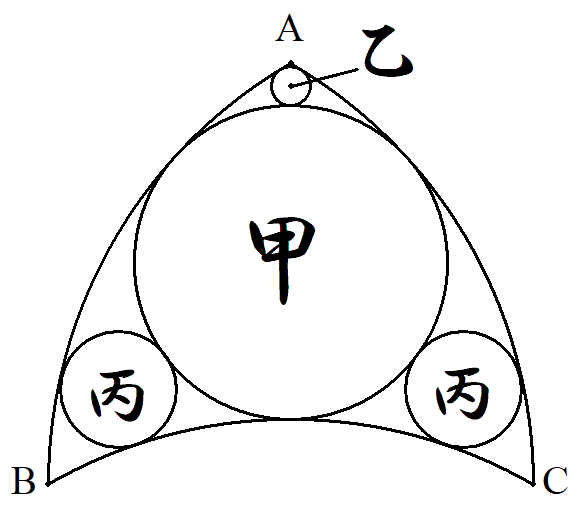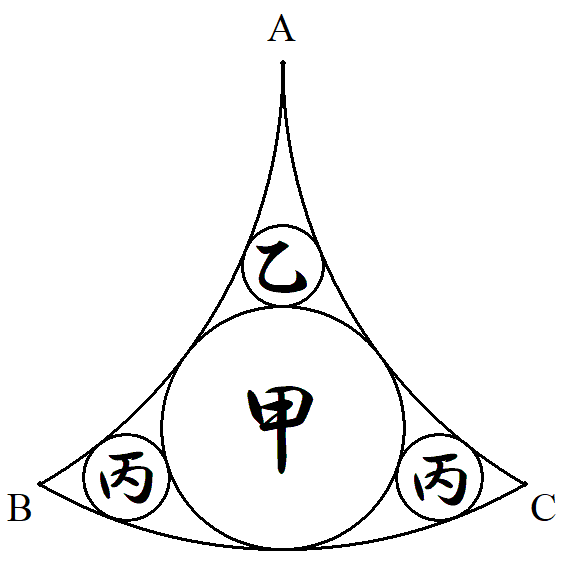  21. A，B，Cは1辺の長さが1の正三角形の頂点で，
    弧CA，ABは半径1の円弧である。
    この図形の中に図のように互いに接する甲乙丙
    丁円を配置する。
    甲乙丙丁円の半径をそれぞれ求めよ。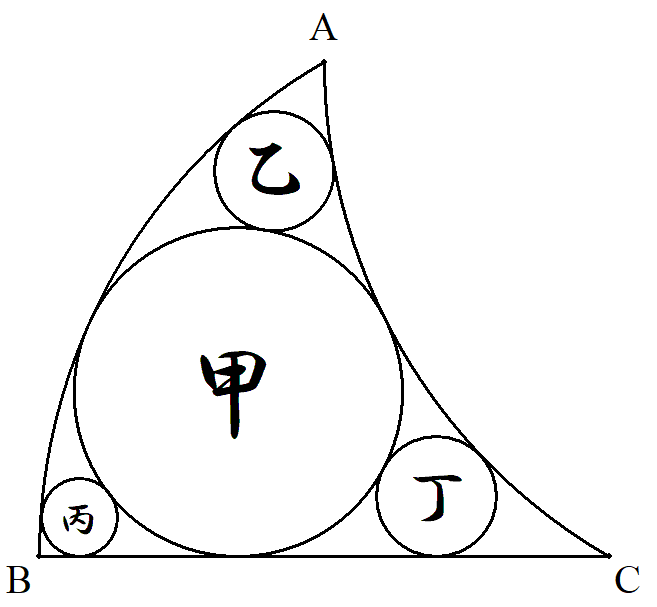



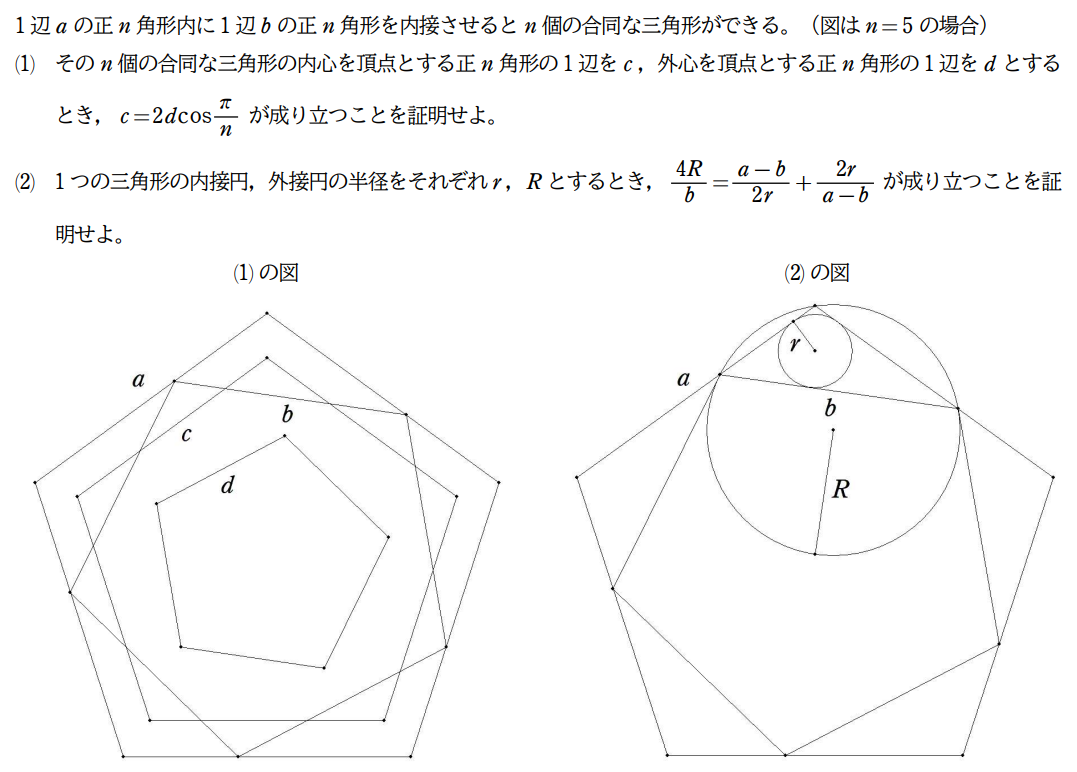
  22. 1辺の長さがaの正n角形の中心を中心とする大円は，
    各辺と2点で交わっている。
    その隙間に，図のように1個の赤円と(n+2)個の黄円
    を入れる。
    このとき，π/n＝θとして，大円，赤円，黄円の半径を
    それぞれ求めよ。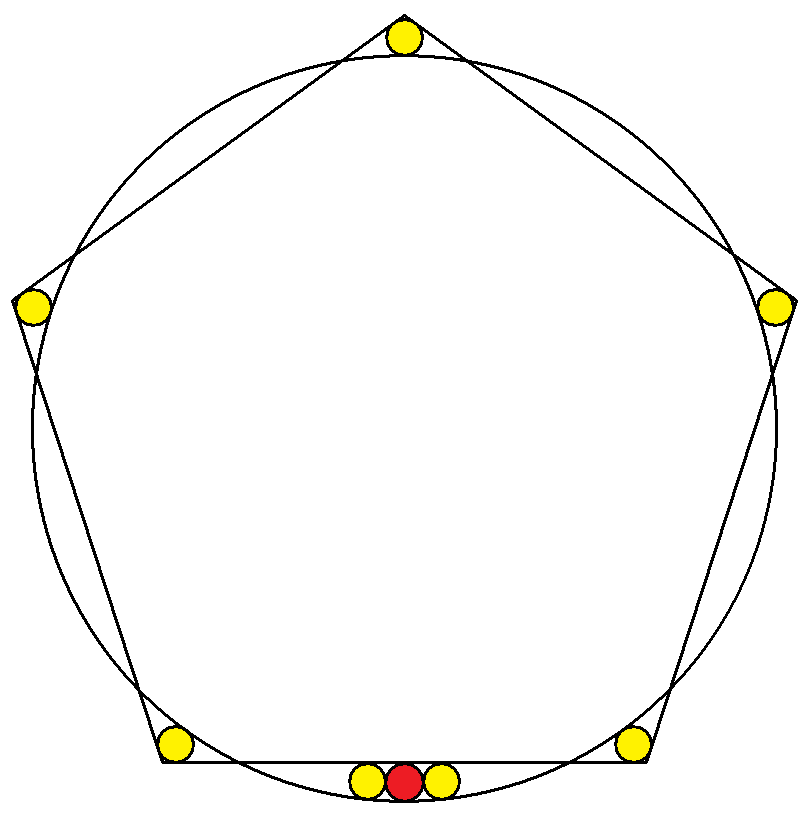



  23. 図のように正三角形と正方形が重なっており，
    その隙間に5個の等円が入っている。
    等円の半径が1のとき，正三角形と正方形の1
    辺の長さをそれぞれ求めよ。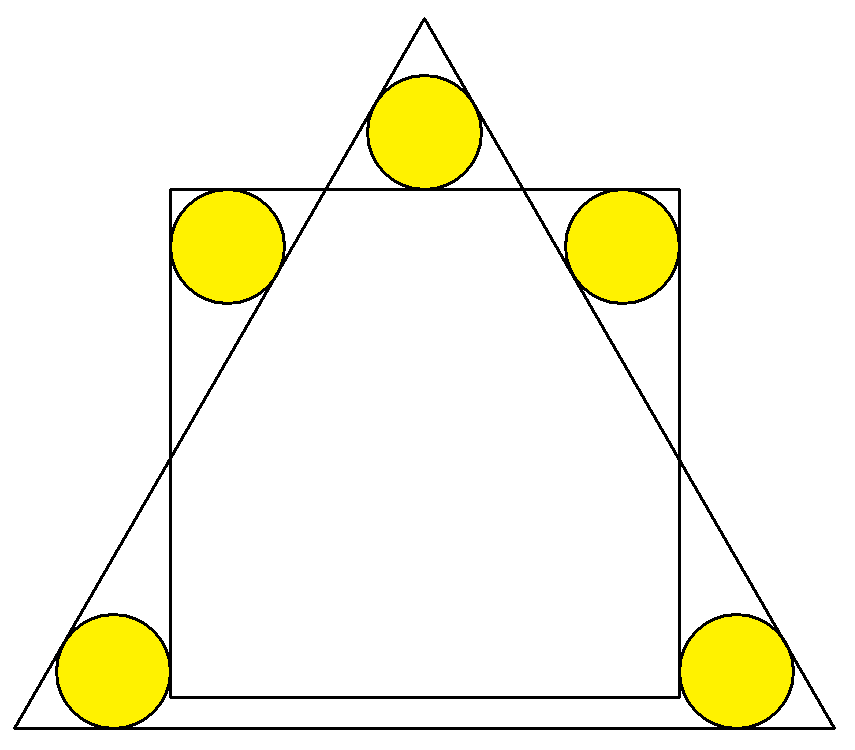



  24. 1辺の長さが1の正三角形と大円が重なっている。
    その隙間に図のように赤円1個，青円2個，黄円
    5個が入っている。大円の半径を求めよ。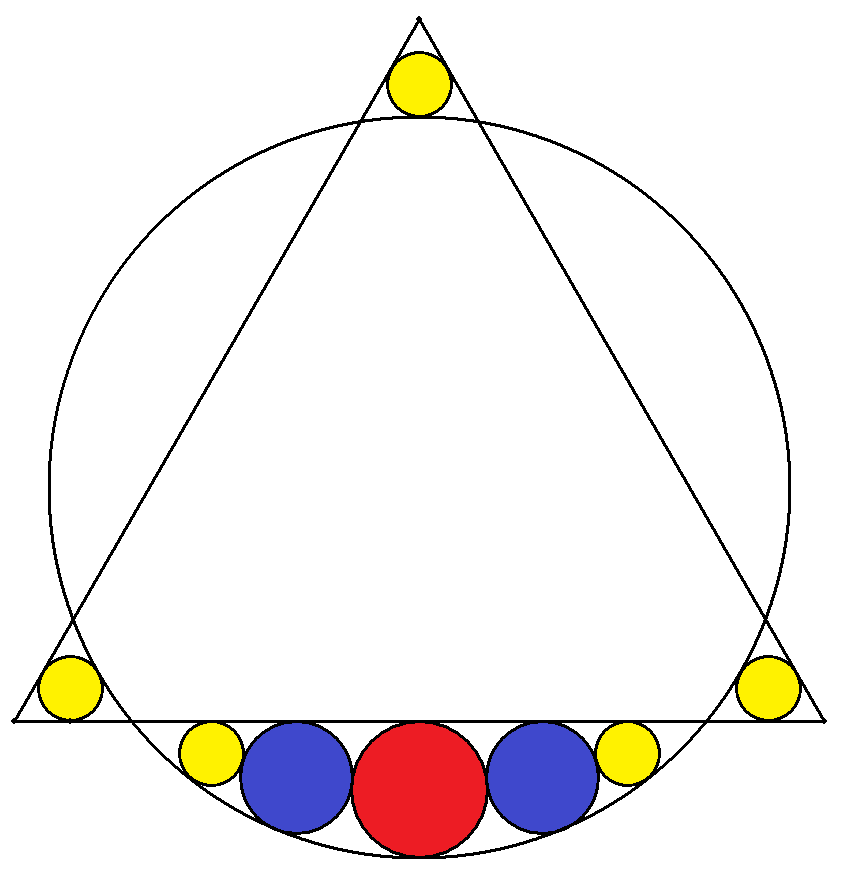



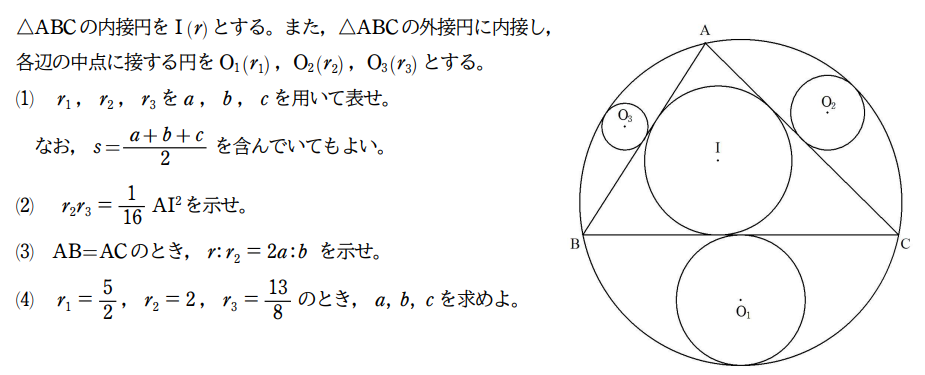
  25. 四角形ABCDの対角線の交点をEとし，
    △ABE，△BCE，△CDE，△DAEの
    内接円をそれぞれO1(r1)，O2(r2)，
    O3(r3)，O4(r4)とする。
    AB＝AE，∠BAC＝60°，∠BDC＝90°，
    r1＝r3のとき，比r2：r4を求めよ。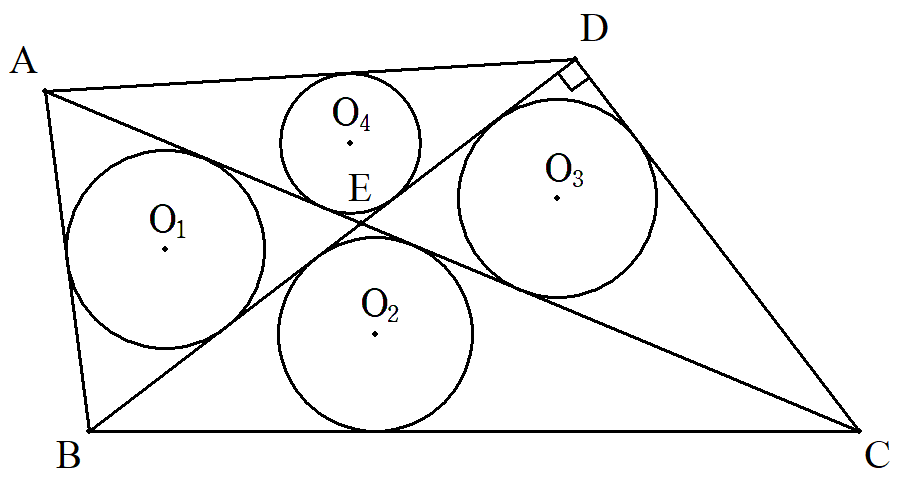



  26. 四角形ABCDの対角線の交点をE，
    AからBEに下した垂線の足をFとする。
    △ABEが正三角形，∠CDE＝90°，
    △ABEと△CDEの内接円の半径が等しいとき，
    AF＋BF＝CDを示せ。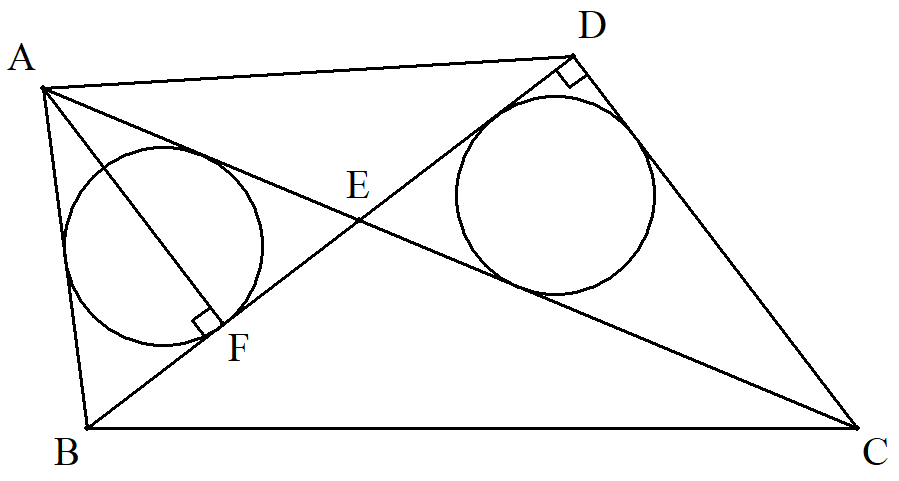



  27. BC＝5，CA＝8，AB＝7の△ABC
    のBC，CA，AB上にそれぞれ点D，
    E，Fを，ED∥AB，FD∥ACとなる
    ようにとる。
    △FBD，△EDC，△DEFに内接円
    を描く。AB，AC上にそれぞれG，H
    をとり，GHが3円の接線になるとき，
    BDを求めよ。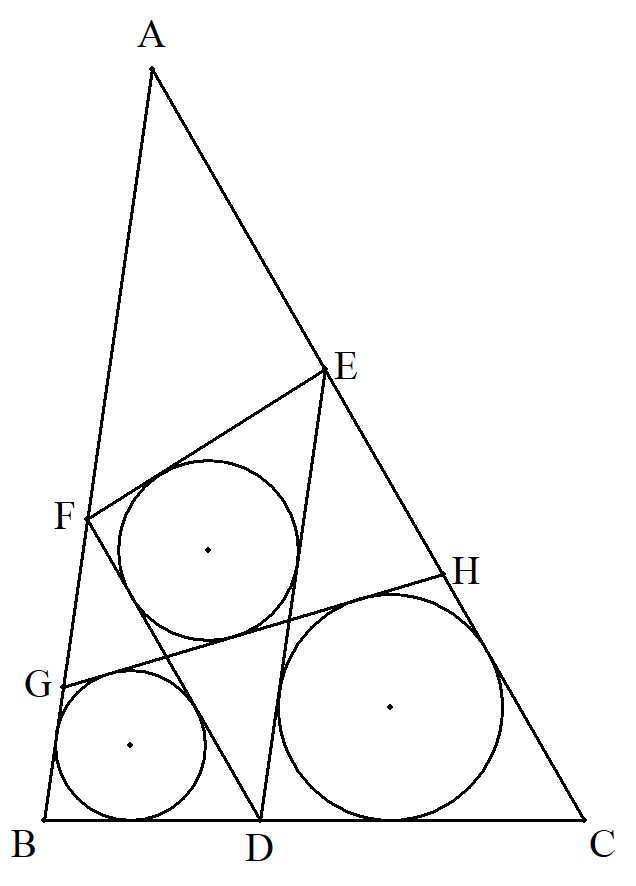



  28. 四角形ABCDの対角線の交点をEとし，△ABE，
    △CDEの内接円の中心をそれぞれP，Qとする。
    AからBEに下した垂線の足をF，内接円PとAB
    との接点をGとし，AF＝f，AG＝gとおく。
    AB＝AE，∠CDE＝90°，円P，Qの半径が等しい
    とき，四角形の面積をf，gを用いて表せ。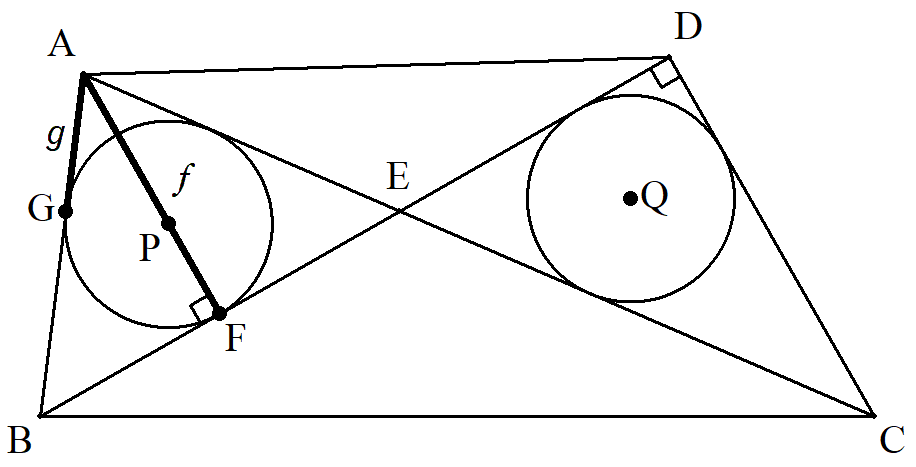



  29. BC＝a，CA＝40，AB＝33の△ABC
    のBC，CA，AB上にそれぞれ点D，
    E，Fを，ED∥AB，FD∥ACとなる
    ようにとる。
    △FBD，△EDC，△DEFに内接円
    を描く。AB，AC上にそれぞれ点G，
    Hを，GHが3円の接線となるように
    とる。このとき，
    (1)　aの値の範囲を求めよ。
    (2)　BDを求めよ。
    (3)　BDが1通りの場合のaの値を
    　　求めよ。
    (4)　(3)のとき，BD，EFをそれ
    　　ぞれ求めよ。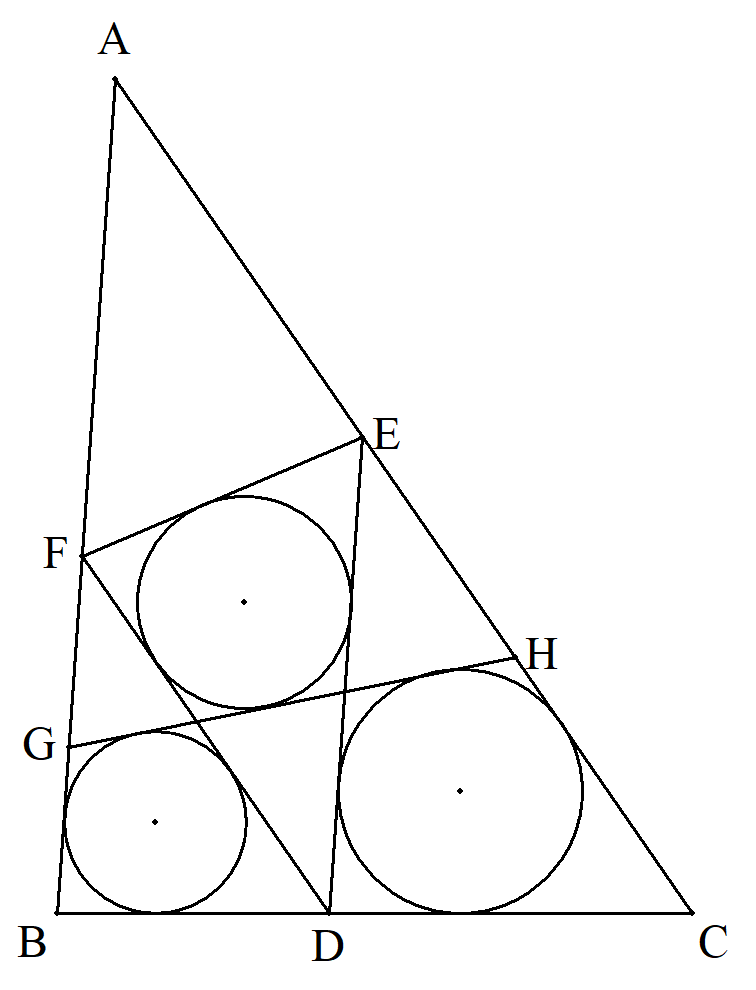



  30. 図のようにひし形内に甲乙円が2個ずつ入っている。
    甲円に接するひし形の対角線の長さを2a ，もう一つ
    の対角線の長さを2bとおくとき，甲乙円の半径をそ
    れぞれ求めよ。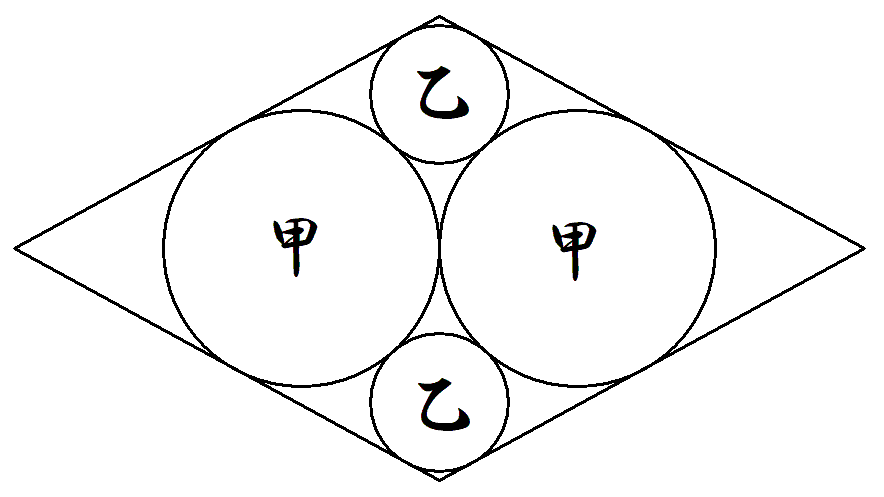



  31. 図のようにひし形内に甲乙円が2個ずつ入っている。
    甲乙円の半径がそれぞれr1，r2のとき，ひし形の面積
    を求めよ。






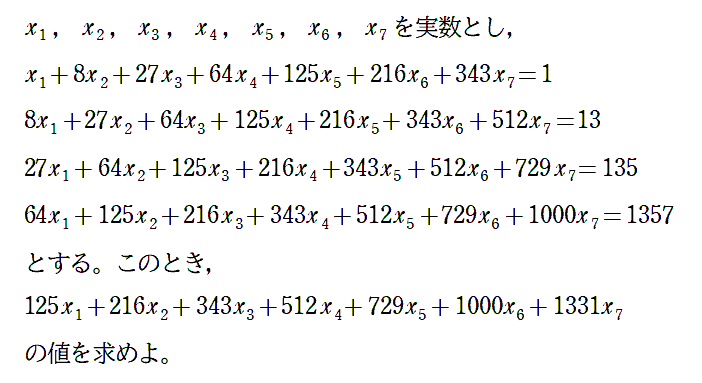
  33. 右図で，26個すべての点を1回だけ通って
    元に戻ってくる経路はあるか。
    あればその経路を1つ示せ。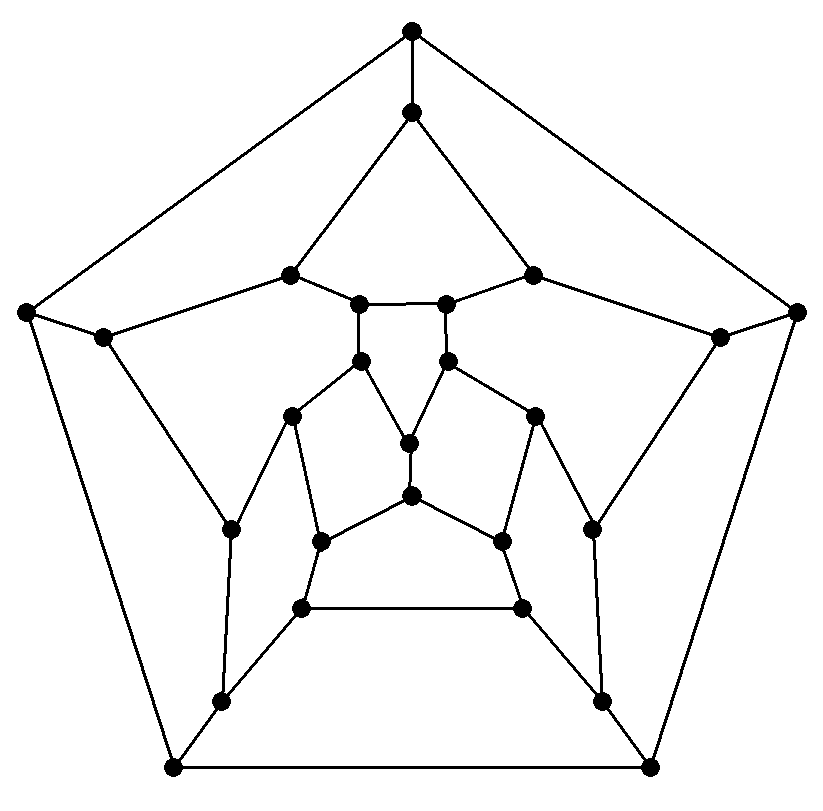






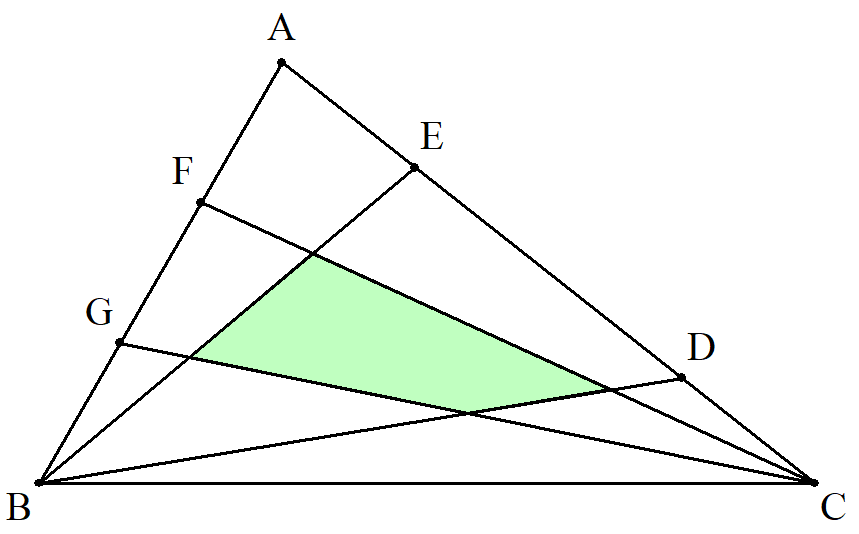
  35. △ABCのCAを1:3，3:1に内分する点
    をそれぞれD，E，ABを1：2，2：1
    に内分する点をそれぞれF，G，FDと
    GEの交点をHとする。
    このとき，△HFG：△HBCを求めよ。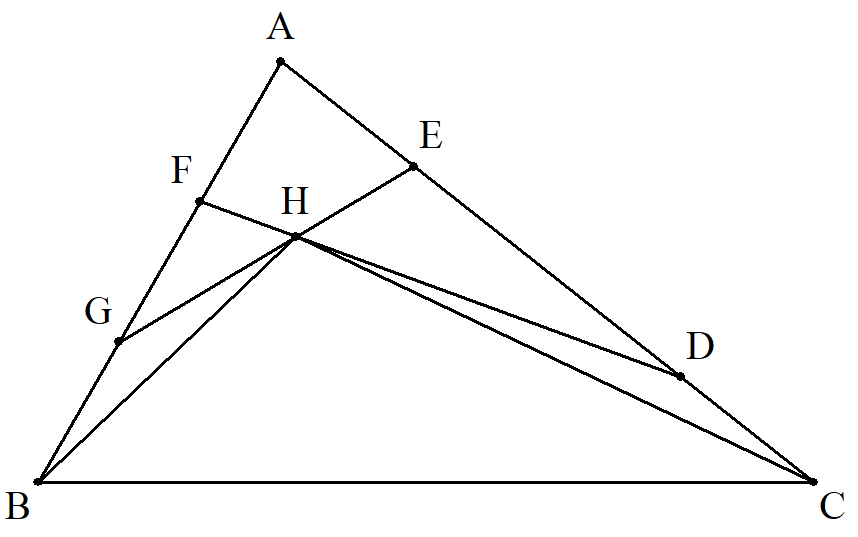









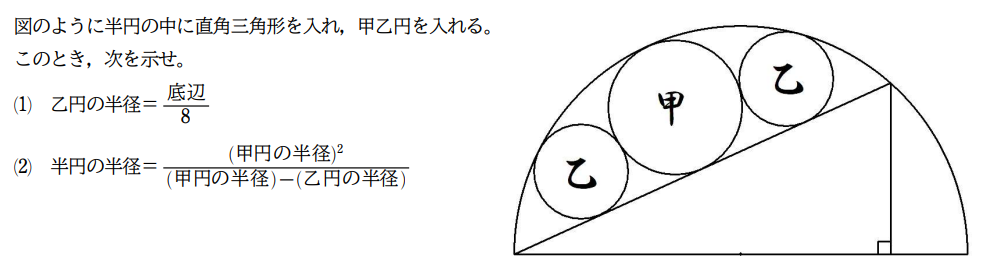
  38. 半円内に直角三角形を描き，その中へ2個の等円を入れる。
    ただし，左側の等円は斜辺の中点で接している。
    このとき，直角三角形の底辺を知って高さを求めよ。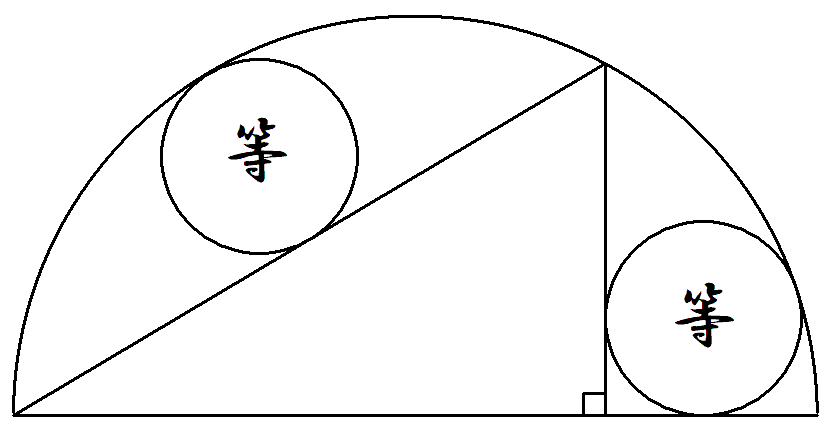









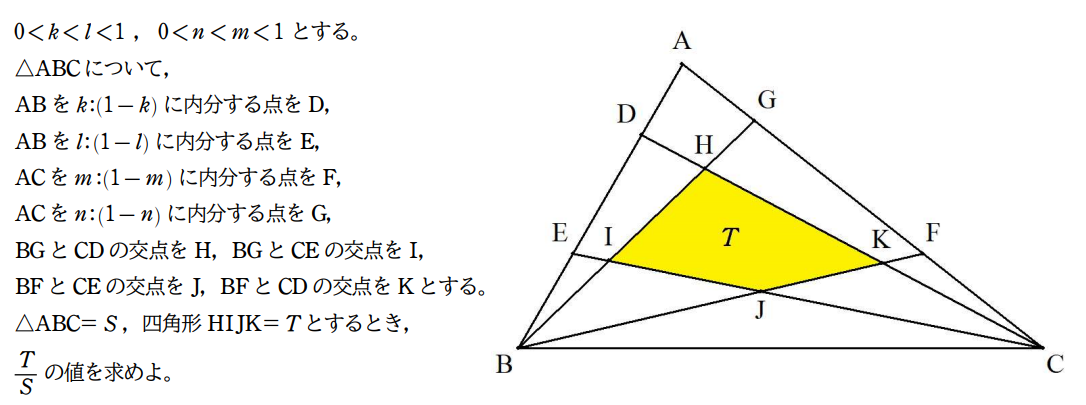
  41. 半円内に直角三角形を描き，その中に甲円2個，
    乙円2個，丙円1個，丁円1個を入れる。
    甲円の半径を知って，乙円，丙円，丁円の半径
    を求めよ。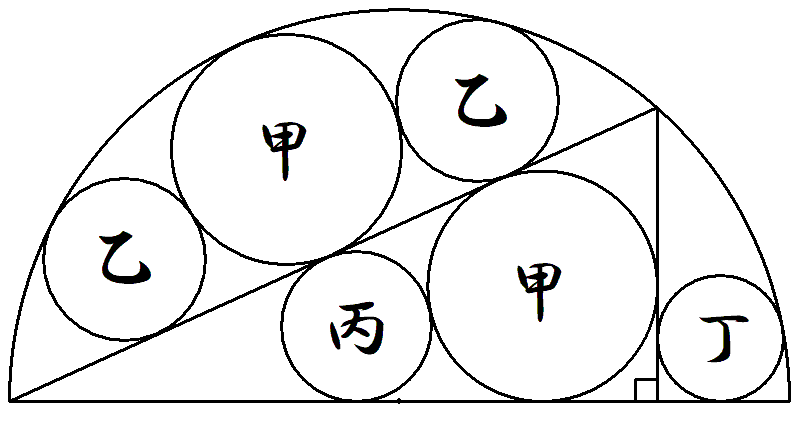



  42. 半円内に直角三角形を描き，その中に斜辺に接する
    甲円1個，乙円2個，丙円2個を入れる。
    直角三角形の底辺をa，高さをbとおくとき，
    半円，甲円，乙円，丙円の半径をそれぞれ求めよ。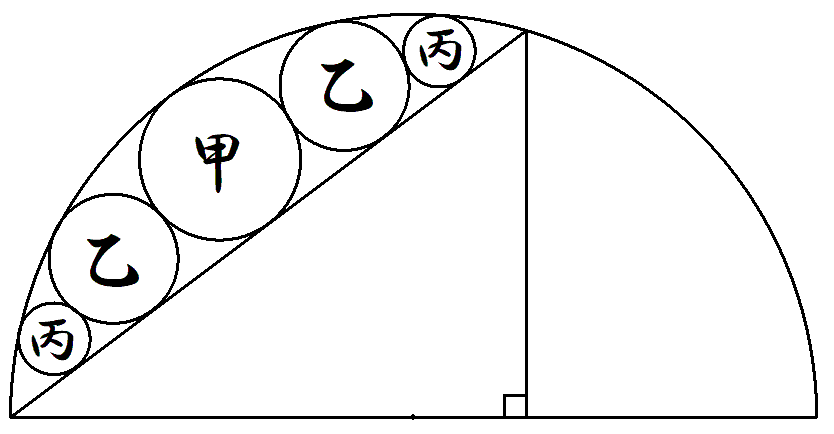