(1) (3-√2)/7,(2) {83+11√2-2√(410+23√2)}/289,(3) {7-2√(10-√2)}/7
近似値:(1) 0.2265409,(2) 0.195445,(3) 0.1628139
(1) (-1+√10)/9,(2) (17+6√2-8√5-√10)/31
近似値:(1) 0.240253,(2) 0.143047
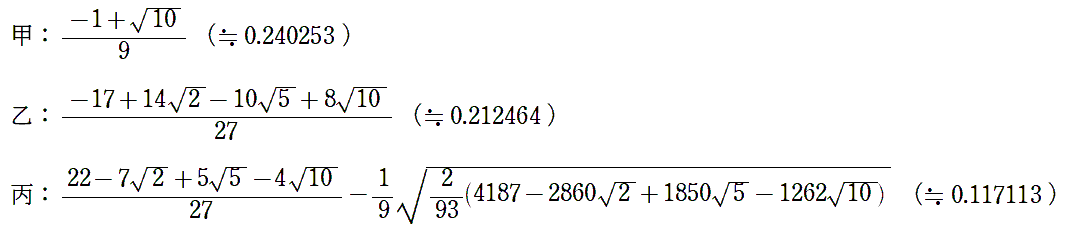
(1) (-13+4√3+√(1790-588√3))/121
(2) R=1+√(3n2-6n+5+2(n-1)√3)

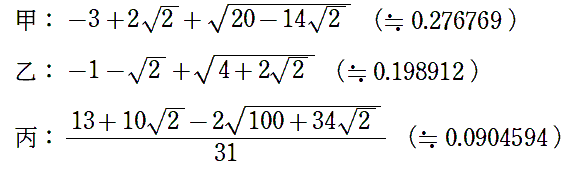
甲√2-1,乙5√2-7,丙(5√2-1)/49,丁(√2-1)/8
甲(-1+√10)/9,乙(55-10√10)/81
省略
省略
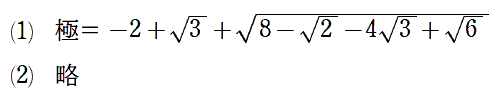
a+b-√(a2+b2)
証明略
(5+3√2)π/8
(1) 4S+a2+b2+c2
(2) 19S+4(a2+b2+c2)
6(n)
(例)[√444444]=666
2b
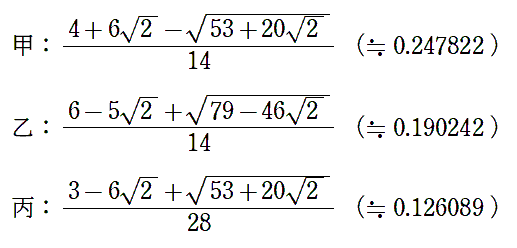
乙:1/3
丙:(4√2-5)/3
甲:1/2
乙:(√2-1)/2
丙:(3-2√2)/2
乙:(2-√2)/2
丙:(2-√2)/4
甲:√2-1
乙:2√2-1-2√(2-√2)
(3-√2)/7
{2+√2-2√(1+√2)}/2
a{√(2+a)-√(2a)}/{2√(2-a)}
(√3-√2)/2
※ A527の一般化。a=√2とすると,A527の答えが得られる。
(1) √{(s-a)(s-b)(s-c)(s-d)}
(2) √{(ab+cd)(ac+bd)(ad+bc)}/4S
(3) (a+c)(b+d)(ac+bd)/8S
※ (3)のヒント:PR⊥QSより,S´=(1/2)PR・QS しかし,計算はとても大変である。
2
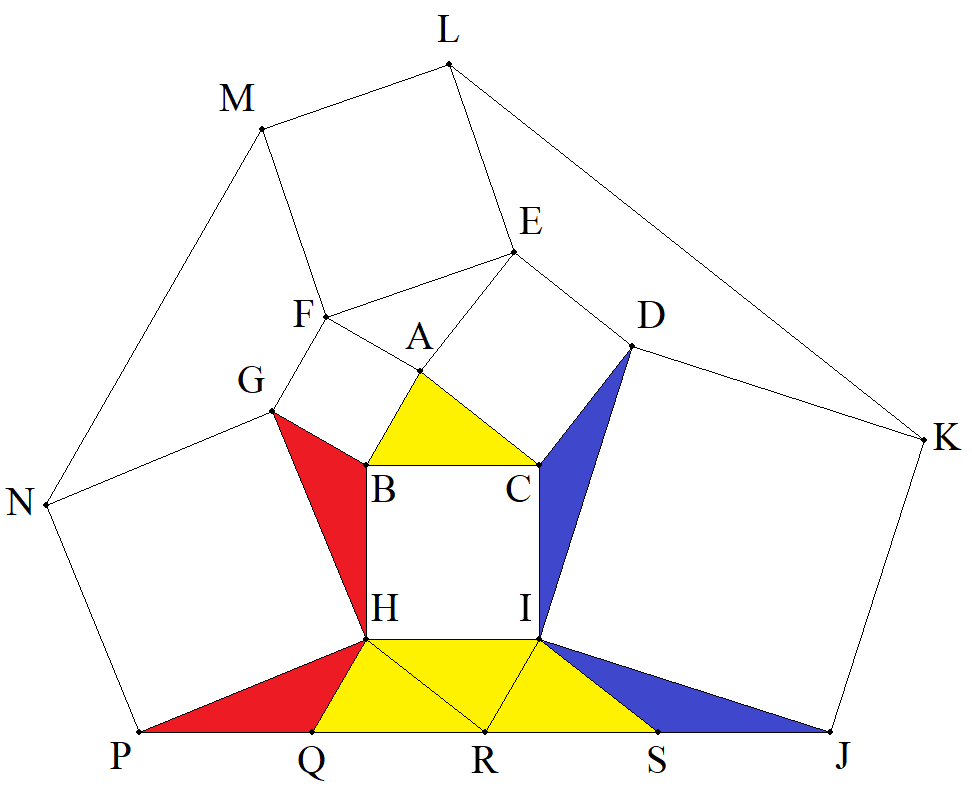
※赤と青の正方形の向きは同じ
略
※AC=BC,AC⊥BCを示し,それを使う。
略
※正方形で囲まれる2つの三角形に余弦定理を適用する。
茶64,黄緑116
※茶の1辺は三平方の定理で求められる。
9
※△AIDの外接円に接弦定理の逆を適用し,方べきの定理を使う。
略
※角の二等分線が直径になることを示す。
16
66…67(6を2019個並べ,最後に7を並べた2020桁の数)
赤52,青85,黄45,緑13
36
甲:(3-√5)/2,乙:√5-2
108°
※AC,CDはABを直径とする円に内接する正五角形の辺である。
(2a-b)(a-b):b(a-b):ab
S1=4(-a2+b2+c2)2S/{(4S-a2+3b2+c2)(4S-a2+b2+3c2)}
S2=c2(4S+a2-b2+c2)/2(4S-a2+b2+3c2)
S3=b2(4S+a2+b2-c2)/2(4S-a2+3b2+c2)
π/2-2π/n
224
{(a2+b2+c2)/(2S)+1}2S
※ωをブロカール角とすると,(2cotω+1)2Sと表すこともできる。
(1) √{(s-a)(s-b)(s-c)(s-d)}
(2) {2S+(a+c)2+(b-d)2}{2S+(a-c)2+(b+d)2}/4S
40419/91
1235(項)
(1) AB=(c+bcosA)/sinA,AD=(b+ccosA)/sinA
(2) S={2bc+(b2+c2)cosA}/(2sinA)