(1) 56√2/81
(2) (407008+237907√2)/2576
(1) 5√15/2
(2) (900+269√15)/30
(1) 45√55/2
(2) (31377060+4848995√55)/59202
tanα=1/(√(n+1)-√n)=1/tanβ=tan(90°-β)であるから,
α=90°-βより,(α+β)/3=30° …(答)
EM=8
1465
b2/4
-x3-2x2-x-1
偶数
赤 (5-2√5)/15,青 (15-4√5)/15
FB=3,BD=√19,DF=√7
略
18
√(a2+b2+c2+d2-e2-f2)/2
4
√601/14
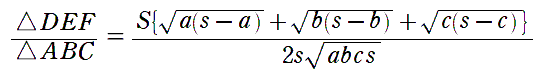
3√3-5
8019/40
{1+√(1+4tan2θ)}/2tanθ
(1) a2+c2=b2+d2
(2) (ab+cd)(ad+bc)/(a2+c2),AB=(ad+bc)/√(a2+c2),AD=(ab+cd)/√(a2+c2)
(3) 0<a≦b≦d≦cのとき,(a+d)√(b2-a2),AB=√(b2-a2),AD=a+d
30°
2π
7
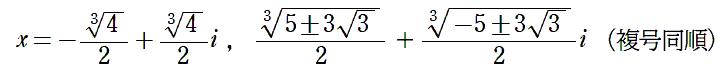
7√3-12
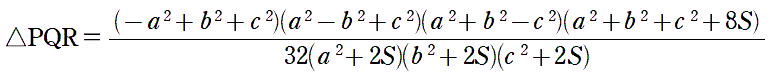

16(3-2√2)
1/√戊=(1/2√2)(1/√己+1/√康)
(1+√3+√(3√3))/3
19°
甲乙丙円の半径をそれぞれr1,r2,r3とすると,
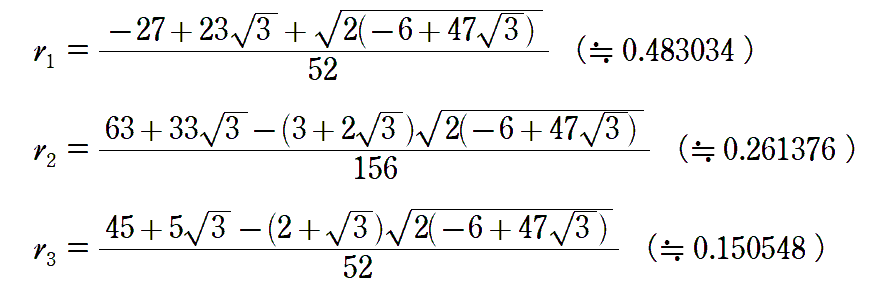
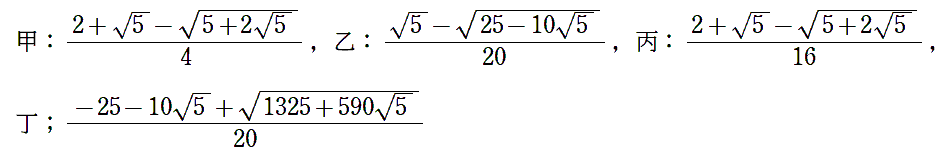
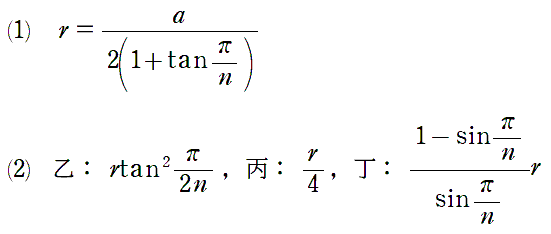
6/23
(1) √3+1
(2) √3-1
(6+√2)/5
7√2
1/4
(1) √(50-10√5)/20
(2) 接する