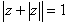(1) sin3α+sin3β+sin3γ=-12sinαsinβsinγ=3sin(α+β+γ) を証明せよ.
(2) cos3α+cos3β+cos3γ=12cosαcosβcosγ=3cos(α+β+γ) を証明せよ.
(3) (1+cosαcosβ)2+(1+cosβcosγ)2+(1+cosγcosα)2の値を求めよ.
(1) cosθcos3θcos5θ
(2) sinθsin2θsin3θ
(1)
∠ABD=20°,∠DBC=60°,
∠BCA=50°,∠ACD=30°
(2)
∠ABD=20°,∠DBC=60°,
∠BCA=30°,∠ACD=50°
(3)
∠ABD=14°,∠DBC=14°,
∠BCA=34°,∠ACD=73°
(4)
∠ABD=20°,∠DBC=60°,
∠BCA=65°,∠ACD=15°
(1) fn(x) は x2+1を因数にもつことを証明せよ.
(2) すべての実数xに対して,f4(x)>0 となるように,sinθ の値の範囲を求めよ.
z=a sin x sin y+b sin x cos y+ccos x sin y+d cos x cos y
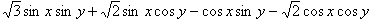 の最大・最小値を求めよ.
の最大・最小値を求めよ.ただし,
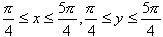 とする.
とする.
(1) x3+y3+z3-3xyz をx,y,zの1次式の積の形に表せ.
(2) 3次方程式x3-3uvx+u3+v3=0 を解け.
(3) 3次方程式x3+ax+b=0 を解け.
(4) 3次方程式 x3+px2+qx+r=0の解法を述べよ.
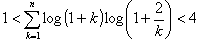 を満たすnの値の個数を求めよ.
を満たすnの値の個数を求めよ.
(1) 0<α<x≦βで,上の関係を満たすxが存在するためのα, β, k の条件を求めよ.
(2)
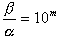 (mは正の整数)のとき,上の関係を満たすxの値の個数を求めよ.
(mは正の整数)のとき,上の関係を満たすxの値の個数を求めよ.(3) 上の関係を満たすxの値がn個あり,小さいものから順に並べて,i 番目の x の値を xi とおくとき,xi を α, k, i を用いて表せ.
(4) (3)で,
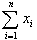 を求めよ.
を求めよ.
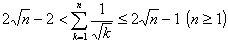 を証明せよ.
を証明せよ.
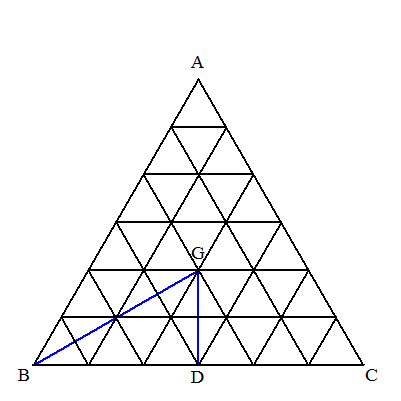
| 一辺の長さが n の正三角形ABCの各辺を n 等分し, 右図のように格子を入れる. このとき,次の問いに答えよ. (1) 大小すべての正三角形の個数を求めよ. (2) 正三角形ABCの重心をG,BCの中点をDとする とき,△GBDに含まれる格子点の個数を求めよ. |
 |
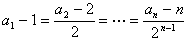 のとき,
のとき,
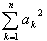 の最小値を求めよ.
の最小値を求めよ.
(1)
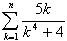
(2)
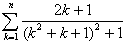
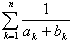 を求めよ.
を求めよ.{an}:a1=-18,a2=-23,an+2=2an+1-an+2n
{bn}:b1=24,bn+1=2bn-n3
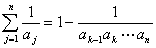
を証明せよ.ただし,n≧k-1 とする.
a(k-1)n+1-a(k-1)n=a(k)n(k=1,2,…,m), a(m)n+1-am)n=0のとき,
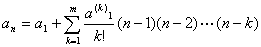
を証明せよ.
この生徒が遅刻をした次の日には90%遅刻をしないが,
遅刻をしなかった次の日には30%遅刻をする恐れがある。
長い間には,この生徒は何%遅刻するか。
(1)
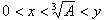 のとき,
のとき,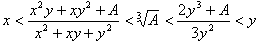
を証明せよ.
(2)
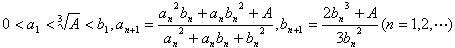
とおくとき,2つの極限値
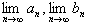
を求めよ.
(1) a0 の値を求めよ.
(2) a-n=an を証明せよ.
(3) an+7m=anを証明せよ.
(4) すべての anは,a0,a1,a2,a3のいずれかに等しいことを証明せよ.
(5) a1=a とおくとき,a2, a3,a4 を a で表せ.
(6) x=a を1つの解にもつ,最低次の有理数係数の方程式 f(x)=0 を求めよ.ただし,多項式f(x) の最高次の項の係数は1である.
(7) f(an) の値を求めよ.
(8)
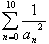 の値を求めよ.
の値を求めよ.(9) an を a の最低次の有理数係数の多項式として表せ.
(1) Cの極値を求めよ.
(2) Cが原点で対称になるように,p, q の値を求めよ.
(3) Cが原点を通り,極大値が0となるように,p, qの値を求めよ.
(4) Cが直線 y=9x に接し,極小値が0となるように,p, q の値を求めよ.
(1) an+3-3an+1+an+2=0 を証明せよ.
(2) a10 の値を求めよ.
x3+ax2+ax+a=0 …1
x3+ax2+ax-a=0 …2
x3+ax2-ax+a=0 …3
x3+ax2-ax-a=0 …4
について,次の問いに答えよ.ただし,aは0でない定数とする.
(1) 相異なる3つの実数解をもつことができる方程式はどれか.またそれはどのようなaの値のときか.
(2) 1~4すべての方程式が,実数解をもたないようなaの値の範囲を求めよ.
(1) max(x, y, z)-min(x, y, z) の取り得る値の範囲を求めよ.
(2) x3+y3+z3 の取り得る値の範囲を求めよ.
また,a=1,b=2,c=3のとき,α10+β10+γ10の値を求めよ。
(1) 0<x<π/2におけるyの最小値と,そのときのxの値を求めよ.
(2) π/2<x<2πにおけるyの最大値と,そのときの sin x, cos x の値を求めよ.
の最小値と,そのときのxの値を求めよ.
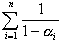
の値を求めよ.
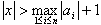 のとき,等式
のとき,等式 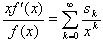 を証明せよ.
を証明せよ.
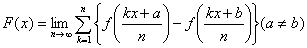
2番目に小さい数を f(x) とおくとき,
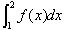 の値を小数第2位まで正しく求めよ.
の値を小数第2位まで正しく求めよ.ただし,f(1)=0 とする.また,x3-x-1=0の実数解をαとおくとき,α=1.3247, α2+3α=5.7290 である.
曲線y=x3+px+q とX軸とで囲まれた部分の面積Sをβの最低次の整式として表せ.
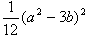 以下であることを証明せよ.
以下であることを証明せよ.
(1) 3次方程式 x3-3x+1=0 を x=r cosθ (r>0,0≦θ≦π)とおいて解け.
(2) 曲線 y=x3-3x+1 とx軸とで囲まれた部分の面積を求めよ.
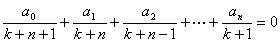
のとき,n次方程式a0xn+a1xn-1+a2xn-2+…+an=0
は,0と1の間に少なくとも1つの実数解をもつことを証明せよ.
点Qもそれに伴って,常にBP上にあり,PO:PA=QP:QBを満足しながらOからBまで動く.
このとき次の問いに答えよ.
(1) 点Qの軌跡の方程式を求めよ.
(2) 点Qの軌跡と線分OBによって囲まれる部分の面積を求めよ.
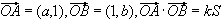 のとき,∠AOBの余弦の値をkを用いて表せ.ただし,Sは△AOBの面積である.
のとき,∠AOBの余弦の値をkを用いて表せ.ただし,Sは△AOBの面積である.
△AOB内に1点Pを次の条件を満たすようにとるとき,
点Pの軌跡の方程式をそれぞれ求めよ.
(1) ∠AOP=∠OBP
(2) ∠AOP=∠ABP
始線上に点Fに対して点Rの反対側に点Aをとり,点F,Aからそれぞれ垂線を立て,曲線の上半分との交点をそれぞれ Q, P とする.
今FA=2,AP=2√3とするとき,次の各々の場合におけるCの曲線名とFRの長さを求めよ.
(1) FQ=1
(2) FQ=2
(3) FQ=3
(4) FQ=4
線分 AB の中点Mの軌跡の方程式を求めよ.
Ax2+2Hxy+By2=cとなった.このとき,次の問いに答えよ.
(1) 次の等式を証明せよ.
[1] A+B=a+b, [2] AB-H2=ab-h2
(2) H=0となるように,回転角θを定めよ.
(3) (2)で,2h(A-B)>0 を証明せよ.
(1)
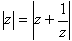
(2)