■Ｂ３（4）の解答例
【中学生レベルで】
辺AB上に∠BCE=30°となる点Eをとる。
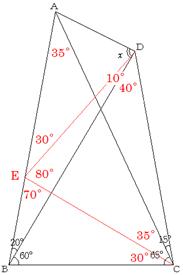
四角形EBCDは(20,60,30,50)の整角四角形であるから∠BDE=10°である。
∵3（2）で証明済み。
∠ECD=∠EDC=50°であるから⊿ECDは二等辺三角形でありEC=ED･･･①となる。
また，∠ECA=∠EAC=35°であるから⊿ECAは二等辺三角形でありEC=EA･･･②である。
①，②よりED=EAとなり，⊿EDAは二等辺三角形となる。
その頂角∠DEA=30°であるから∠EDA=∠EAD=75°となり
∠BDA=∠BDE+∠EDA=10°+75°=85°となる。
（2010/12/06）
【高校レベルで】
⊿ＢＣＤにおいて，∠ＢＤＣ＝180°－（60°＋80°）＝40°である。
⊿ＡＢＤにおいて，･･･①（正弦定理）
⊿ＡＣＤにおいて，･･･②（正弦定理）
⊿ＡＢＣにおいて，･･･③（正弦定理）
①，②，③を辺々掛け合わせると

∴･･･④　である。

ここで，･･･⑤　である。
＜証明は，後述＞
④，⑤より

分母を払って移項すると

三角関数の積和の公式を用いると

両辺に2を掛け､整理すると

三角関数の和積の公式を用いると

であるから
よって　･･･（答）
【⑤の証明】
左辺－右辺

分子

∴　　【終証】
(2010/10/26)