■趣味の数学問題集・Ｂ問題
  1. ｎ人の集団の中に，同じ月日に生れた人のいる確率を求めよ．ただし，2月29日生れの人はいないものとする．
    また，ｎ＝20の場合の確率を，普通の電卓を用いて計算する方法を述べよ。

  2. α+β=u, αβ=v とおくとき，次の等式を証明せよ．
    　　　

  3. 52枚のトランプの中から任意の5枚のカードを引くとき，次のポーカーの役の確率を求めよ．

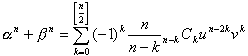
    (1) ワンペア　

    (2) ツーペア　

    (3) スリーカード　

    (4) ストレート　

    (5) フラッシュ　

    (6) フルハウス　

    (7) フォーカード　

    (8) ストレートフラッシュ　

    (9) ロイヤルストレートフラッシュ　

  4. 白球n個の入った袋の中から1個取り出し，代わりに黒球1個を入れる．
    次にまた，その袋の中から1個取り出し，代わりの黒球1個入れる．
    この操作をm回繰り返したとき，袋の中に白球r個残っている確率P(n,m,r) を求めよ．
    ただし，白球，黒球とも同形同質で，袋の中からは同程度に選ばれるものとする．

  5. 下図に含まれる大小すべての正方形，長方形の個数を求めよ．

    　　　

  6. ⊿ABCにおいて，∠ABC=30°，∠ACB=84°である。辺BC上に点Dを∠ADC=54°であるようにとればBD=ACであることを証明せよ。
    BD=AC.GIF

  7. ⊿ABCの辺AB上に点Dを，辺AC上に点Eを，DB=ECとなるようにとる。このとき，四角形DBCEの面積をBC=a，DE=d，∠BAC=Aを用いて表わせ。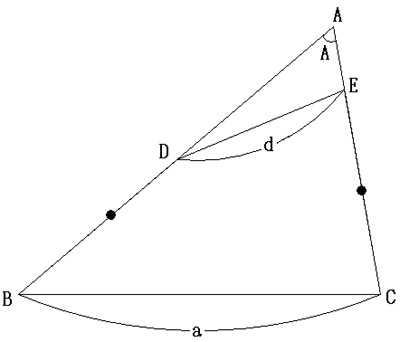

  8. (1)　平行四辺形ABCDと点Eについて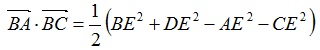，を証明せよ。
    (2)　長方形ABCDと点Eについて，AE2＋CE2＝BE2＋DE2を証明せよ。
    (3)　AB＝4，BC＝5である平行四辺形ABCDの内部に点Eをとる。BE＝3，CE＝DE＝4のとき，AEの長さを求めよ。

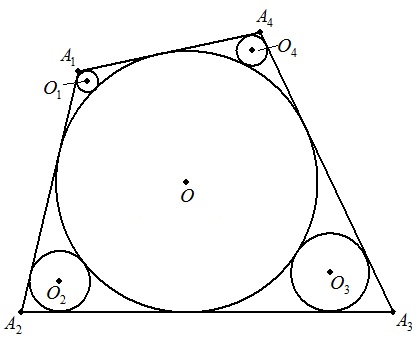
  9. n角形A1A2･･･Anは内接円O(r)をもつ。（n=3，4，5，･･･）
    2辺A1A2，A1Anに接し，円Oに外接する円をO1(r1)，
    2辺A2A3，A2A1に接し，円Oに外接する円をO2(r2)，
    2辺A3A4，A3A2に接し，円Oに外接する円をO3(r3)，
    ････････････････････････････････････････････････
    2辺AnA1，AnAn-1に接し，円Oに外接する円をOn(rn)，
    とする。
    このとき，次を証明せよ。
    (1)　n=3のとき，r=Σ√(r1r2)=√(r1r2)+√(r2r3)+√(r3r1)
    (2)　n=4のとき，r2-(Σ√(r1r2))r+√(r1r2r3r4)=0　（右の図）
    (3)　n=5のとき，r2-(Σ√(r1r2))r+Σ√(r1r2r3r4)=0
    (4)　n=6のとき，r3-(Σ√(r1r2))r2+(Σ√(r1r2r3r4))r-√(r1r2r3r4r5r6))=0

    ただし，n=4のとき，Σ√(r1r2)とは
    √(r1r2)+√(r1r3)+√(r1r4)+√(r2r3)+√(r2r4)+√(r3r4) 　を表す。

  10. ∠C＝90°の直角三角形ABCに，
    図のように3辺に頂点をもつ正三角形PQRを内接させる。
    BC＝a ，CA＝b のとき，PQの長さの最小値を求めよ。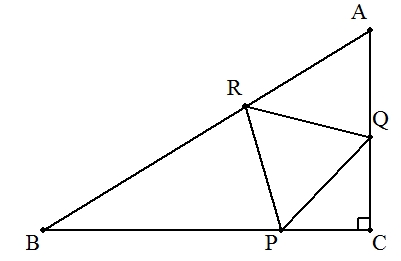

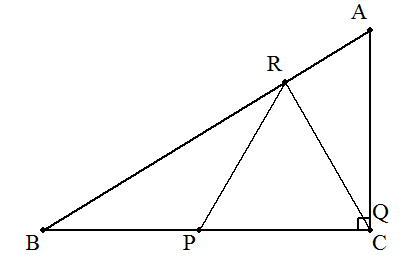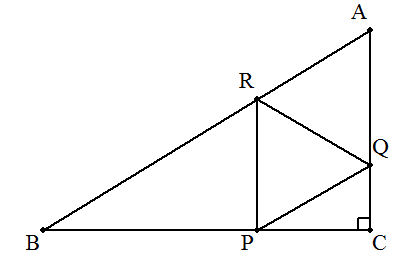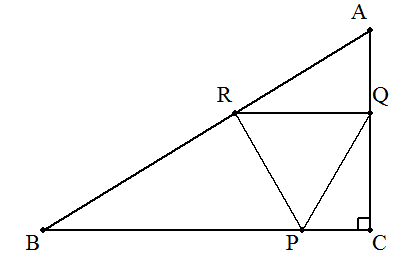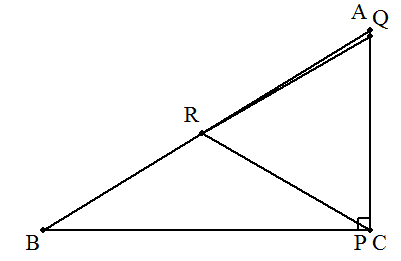  11. △ABCの辺BC上に点Dをとり，DからCA，ABに下ろした垂線の足をそれぞれE，Fとする。
    いま，点Dを四角形AFDEの面積が最大になるようにとる。
    (1)　BD：CDを求めよ。
    (2)　四角形AFDEの面積を求めよ。
    (3)　ADの長さを求めよ。
    (4)　a=7，b=5，c=6のとき，(1)～(3)の値を求めよ。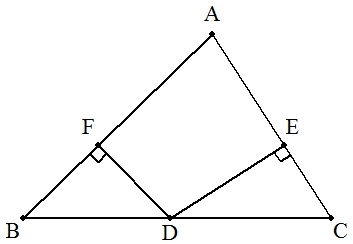

  12. 2n+2個の点A0，A1，･･･，A2n+1はこの順に直線上にあり，AiAi+1=i+1（i=0，1，･･･，2n+1）とする。
    線分A0A2n+1上に2n+2個の半円の直径を図のように配置する。このとき，斜線部分の面積をnを用いて表せ。

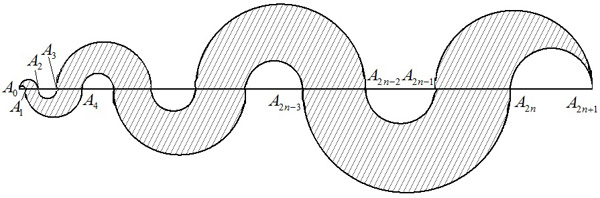
  13. 円に内接する四角形ABCDの対角線の交点をE，
    △EAB，△EBC，△ECD，△EDAの内接円を順に
    O1(r1)，O2(r2)，O3(r3)，O4(r4)とする。
    AB＝4，BC＝6，CD＝5，DA＝3のとき，
    r1：r2：r3：r4を求めよ。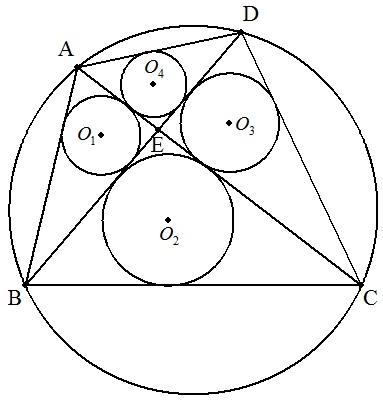

  14. 次の3つの数を小さい順に並べよ。

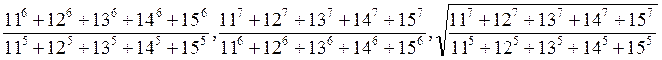
  15. 1辺の長さがaの正n角形A1A2･･･Anの内部にn個の点B1，B2，･･･，Bnをとり，
    図のようにn個の合同な三角形A1A2B1，A2A3B2，･･･，AnA1Bnをつくる。
    これらの三角形の内接円の半径をr1，正n角形B1B2･･･Bnの内接円をr2とする。
    (1)　r1をr2を用いて表せ。
    (2)　r1=r2のとき，r1をaを用いて表せ。
    (3)　n個の半径r1の円の面積の和が，半径r2の円の面積に等しくなるとき，
    r1，r2をaを用いて表せ。

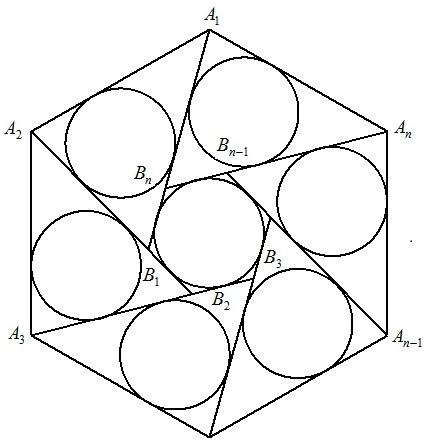  16. 四角形ABCDは内接円と外接円をもつものとする。
    四角形ABCDの外接円，内接円の半径をそれぞれ
    R，r とするとき，R≧√2rを証明せよ。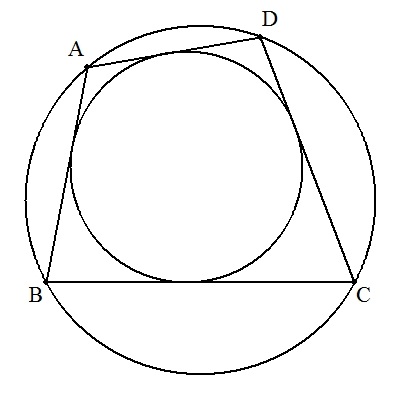

  17. AB＝ACの二等辺三角形ABCについて，辺
    AB，ACを一辺とする正三角形ABD，ACEを
    △ABCと重ならないようにつくる。
    さらに，点FをDA=DF=EFとなるようにとる。
    このとき，次の問に答えよ。
    (1)　AB＝a，BC＝bとおくとき，AFを求めよ。
    (2)　a=2，b=3のとき，AFを求めよ。
    (3)　a=3，b=2のとき，AFを求めよ。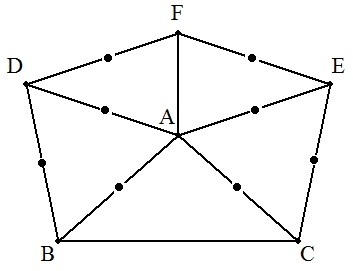

  18. AB＝ACの二等辺三角形ABCについて，辺
    AB，ACを一辺とする正三角形ABD，ACEを
    △ABCと重ならないようにつくる。
    さらに，DEの上側と下側にそれぞれ点F，G
    を，DF＝EF，DG＝EGとなるようにとる。
    AB＝a，BC＝b，DF＝cとおくとき，AF，AGを
    それぞれ求めよ。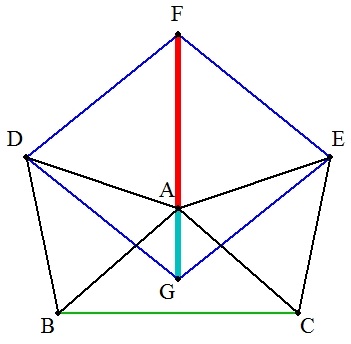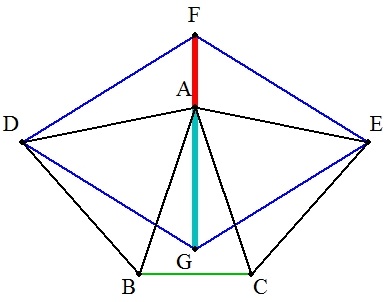

  19. 直角三角形ABCに，図のように正方形CDEFを
    内接させる。△AED，△EBFの内接円の半径を
    それぞれr1，r2とするとき，ABの長さをr1，r2を
    用いて表せ。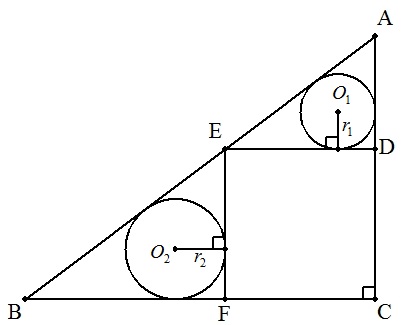

  20. AB=AC=aである直角二等辺三角形ABC内に，
    点Bを中心とする半径aの円弧ADを描く。
    (1)　弧ADに内接し，2辺AB，BCに接する円O1の
    　半径r1を求めよ。
    (2)　弧ADに外接し，2辺BC，CAに接する円O2の
    　半径r2を求めよ。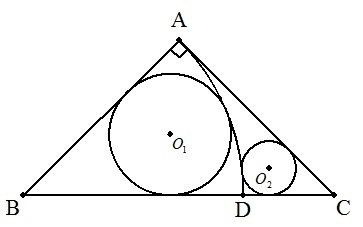

  21. 二等辺三角形ABCの辺BCの中点をMとする。
    この三角形の内接円をO1(r1)，
    円O1に外接し，AB，AMに接する円をO2(r2)，AC，AMに接する円をO2'(r2)，
    2円O2，O2'に外接し，AB，ACに接する円をO3(r3)，
    円O3に外接し，AB，AMに接する円をO4(r4)，AC，AMに接する円をO4'(r4)，
    ･･･，と連結する円を三角形ABC内に描いていく。
    AB＝25，BC＝14のとき，
    (1)　r1，r2，r3，r4を求めよ。
    (2)　r2n-1，r2n（n=1，2，3，･･･）を求めよ。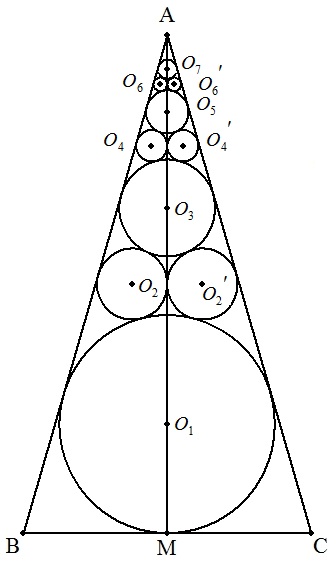

  22. 線分A0Anを直径とする半円の周上をn等分し，その分点をA0に近い方から
    A1，A2，･･･，Ak，･･･，An-1とする。
    △A0AkAk+1の内接円をOk，その半径をrkとする。（k=1，2，･･･，n-1）
    A0An=2r，π/(2n)=θとおくとき，rkをr，k，θを用いて表せ。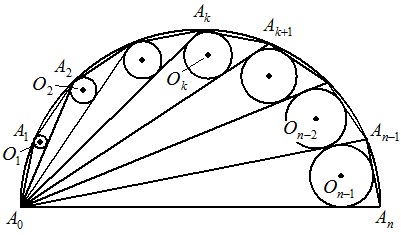

  23. 1辺の長さがaである正三角形ABC内の点Pから3辺BC，CA，ABに
    下ろした垂線の足を順にD，E，Fとする。
    AF＝p，BD＝qとおくとき，次の問に答えよ。
    (1)　CE，AEの長さを求めよ。
    (2)　AP，BP，CPの長さを求めよ。
    (3)　DE，EF，FDの長さを求めよ。
    (4)　△DEFの面積を求めよ。
    (5)　△DEFの内接円の半径を求めよ。
    （A問題88の一般化）

  24. BC＝5，CA＝4，AB＝3である△ABCの2辺AB，BCに接する
    半径1/2の円O1に外接し，2辺BC，CAに接する円O2の半径を
    求めよ。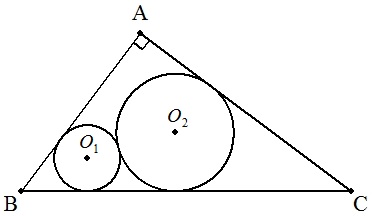

  25. 図のように楕円が，辺が長軸と短軸に平行な長方形ABCDに
    内接している。長方形の4隅の4円が長方形に内接し楕円に
    外接している。4円と楕円の4接点を頂点とする長方形PQRS
    の面積を求めよ。ただし，AB=2a，BC=2bとする。  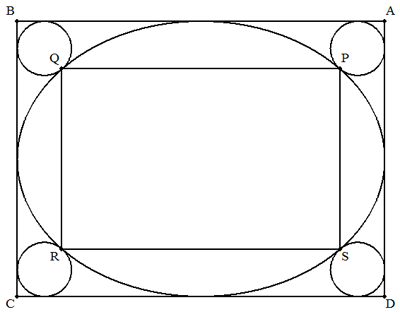  		b_75.png

  26. 正五角形ABCDEの各頂点が，右の図のように点Aはy軸上に，
    点B，Eはy=x2上に，点C，Dはy=2x2上にある。
    ただし，点Aのy座標は正，点B，Cのx座標は負，CDとx軸は
    平行である。 このとき，頂点A，B，Cの座標をそれぞれ求めよ。  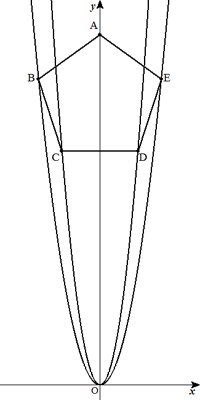  		b_76.png

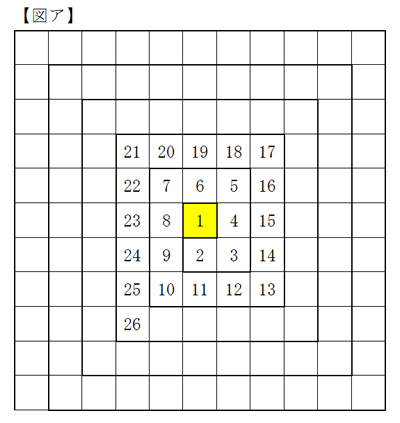
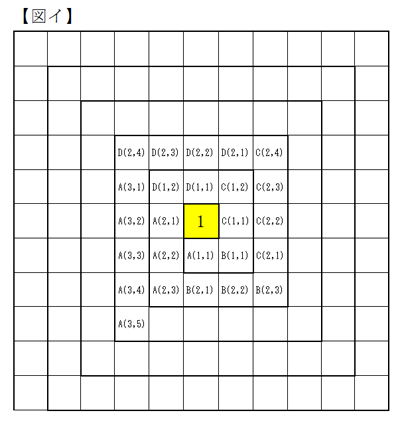
  27. 自然数「1」を中心として，図アのように反時計回りに渦のように自然数を並べていく。
    それらの数字の位置を図イのように表す。次の問いに答えよ。
    (1)　2014の位置を求めよ。
    (2)　D(m,n)＝D(n,m)＋2014を満たすm,nを求めよ。
    　

  28. p，q，rは整数で，3次方程式 x3+px2+qx+r=0の3つの解をα，β，γとする。
    (1)　p が5の倍数のとき，α5＋β5＋γ5 も5の倍数となることを証明せよ。
    (2)　p が7の倍数のとき，α7＋β7＋γ7 も7の倍数となることを証明せよ。
    (3)　p が9の倍数のとき，α9＋β9＋γ9 は9の倍数とは限らないことを証明せよ。
    (4)　p が11の倍数のとき，α11＋β11＋γ11 も11の倍数となることを証明せよ。


  29. 正五角形ABCDEを図のように線分AP，BQ，CR，DS，ETで分割する。
    このときできる5個の三角形はすべて合同で，中央にできる五角形
    PQRSTは正五角形になるものとする。また，CDの中点をMとし，
    ∠PAM＝αとおく。⊿ABPと正五角形PQRSTの面積が等しくなるとき，
    sinαの値を求めよ。  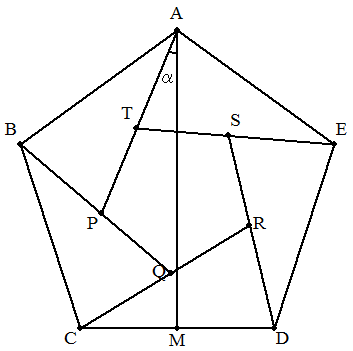   		b_79.png

  30. (1) 正三角形ABCを図のように線分AP，BQ，CRで分割する。このときできる
    ⊿ABP，⊿BCQ，⊿CARはすべて合同で，中央にできる⊿PQRは正三角形に
    なるものとする。また，BCの中点をMとし，∠PAM＝αとおく。⊿ABPと
    正三角形PQRの面積が等しくなるとき，sinαの値を求めよ。  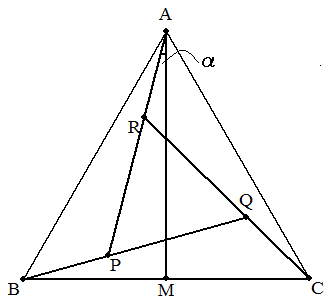   		b_80_1.png
    (2) 正方形ABCDを図のように線分AP，BQ，CR，DSで分割する。このときできる
    4個の三角形はすべて合同で，中央にできる四角形PQRSは正方形になるも
    のとする。また，∠PAC＝αとおく。⊿ABPと正方形PQRSの面積が等しくな
    るとき，sinαの値を求めよ。  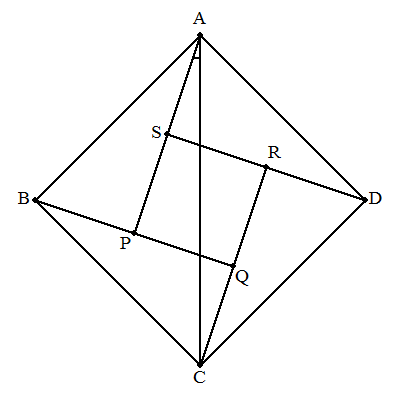   		b_80_2.png
    (3) 正六角形ABCDEFを図のように線分AP，BQ，CR，DS，ET，FUで分割する。
    このときできる6個の三角形はすべて合同で，中央にできる六角形PQRSTU
    は正六角形になるものとする。また，∠PAD＝αとおく。⊿ABPと正六角形
    PQRSTUの面積が等しくなるとき，sinαの値を求めよ。  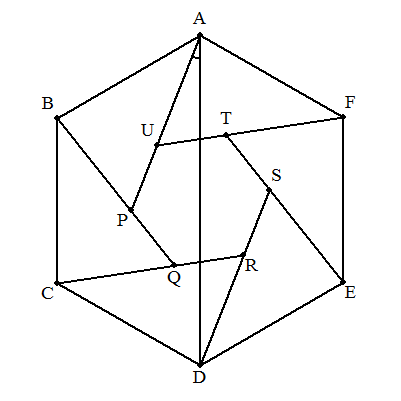   		b_80_3.png
    (4) 正n角形A1A2･･･Anを図のようにn個の線分A1B1，A2B2，･･･，AnBnで分割する。
    このときできるn個の三角形はすべて合同で，中央にできるn角形B1B2･･･Bn
    は正n角形になるものとする。また，正n角形の中心をOとし，∠B1A1O＝αと
    おく。
    ⊿A1A2B1と正n角形B1B2･･･Bnの面積が等しくなるとき，sinαの値を求めよ。  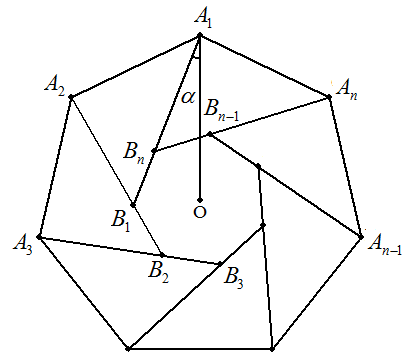   		b_80_4.png

  31. 次の漸化式から一般項anを求めよ。
    (1)　a1=a2=1，a3=2，an+3+an+2-4an+1-4an=0
    (2)　a1=1，a2=2，a3=3，a4=4，an+4-10an+3+35an+2-50an+1+24an=0
    (3)　a1=1，a2=2，a3=3，a4=4，a5=5，an+5-3an+4-5an+3+15an+2+4an+1-12an=0




  32. θは自然数の鋭角とする。
    tanθ＝tanαtanβtanγ（α，β，γはθと異なる自然数の鋭角で，α＜β＜γ）･･･①
    と表す方法を述べよ。
    また，①の形に表すことができない角を求めよ。

  33. 次の問に答えよ。
    (1)　sin20°sin40°sin80°の値を求めよ。
    (2)　cos5°cos55°cos65°の値を求めよ。
    (3)　tan15°tan25°tan35°＝tanθを満たす鋭角θを求めよ。

  34. 3次方程式x3+px2+qx+r=0の相異なる3つの解をα，β，γとする。
    このとき，an=Aαn-1+Bβn-1+Cγn-1，
    A={a3-(β+γ)a2+βγa1}/{(α-β)(α-γ)}，
    B={a3-(γ+α)a2+γαa1}/{(β-γ)(β-α)}，
    C={a3-(α+β)a2+αβa1}/{(γ-α)(γ-β)}は，
    漸化式an+3+pan+2+qan+1+ran=0を満たすことを証明せよ。
    ただし，a1，a2，a3は既知とする。

  35. 4次方程式x4+px3+qx2+rx+s=0の相異なる4つの解をα，β，γ，δとする。
    このとき，an=Aαn-1+Bβn-1+Cγn-1+Dδn-1，
    A={a4-(β+γ+δ)a3+(βγ+γδ+δβ)a2-βγδa1}/{(α-β)(α-γ)(α-δ)}，
    B={a4-(γ+δ+α)a3+(γδ+δα+αγ)a2-γδαa1}/{(β-γ)(β-δ)(β-α)}，
    C={a4-(δ+α+β)a3+(δα+αβ+βδ)a2-δαβa1}/{(γ-δ)(γ-α)(γ-β)}，
    D={a4-(α+β+γ)a3+(αβ+βγ+γα)a2-αβγa1}/{(δ-α)(δ-β)(δ-γ)}は，
    漸化式an+4+pan+3+qan+2+ran+1+san=0を満たすことを証明せよ。
    ただし，a1，a2，a3，a4は既知とする。

  36. AD∥BC，AD<BCである台形ABCDに，図のように3個の等円
    P，Q，Rが内接している。DA＝3，AB＝5，BC＝8，CD＝6のと
    き，等円の半径を求めよ。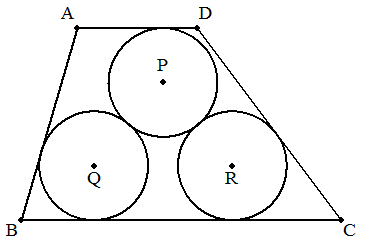

  37. 0°<θ<90°のとき，次の三角方程式を解け。
    (1)　tanθ＝tan2θtan3θtan4θ
    (2)　tanθ＝tan3θtan5θtan7θ

  38. 次の等式を証明せよ。
    tan1°tan2°tan3°・・・tan10°=tan3°tan6°tan9°・・・tan27°×tan20°tan21°tan22°・・・tan40°

  39. AB<BCである四角形ABCDの対角線は点Eで45°で交わり，
    それぞれ∠B，∠Cの二等分線になっている。
    AB＝a，BC＝bのとき，次の問に答えよ。
    (1)　∠EBC＝α，∠ECB＝βとおくとき，tanα，tanβの
    　　値を求めよ。
    (2)　CD，DA，AC，BDを求めよ。
    (3)　AE，BE，CE，DEを求めよ。
    (4)　△EBC，四角形ABCDの面積をそれぞれ求めよ。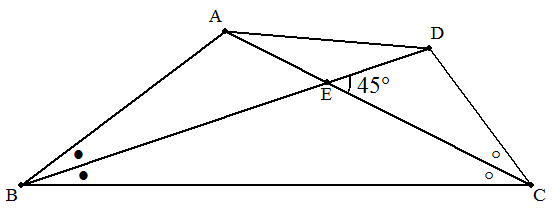

  40. BC＝a，CA＝b，AB＝cである三角形ABCについて，
    BCをk：(1-k)(0<k<1)に内分する点をP1，
    BP1をk：(1-k)に内分する点をP2，
    BP2をk：(1-k)に内分する点をP3，
    ・・・・・・・・・・・・・・・・・・・・・・・・・・・・
    BPnをk：(1-k)に内分する点をPn+1，
    ・・・・・・・・・・・・・・・・・・・・・・・・・・・・
    とするとき，APn2を求めよ。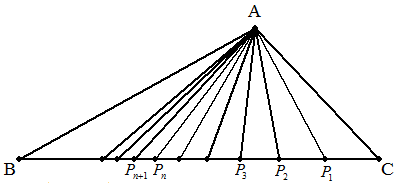

  41. 曲線y＝(x－α)m(x－β)nとx軸とによって囲まれた部分の面積Sを求めよ。
    ただし，m,nは正の整数，α<βとする。


  42. 上底の半径r，下底の半径kr（k>1），高さがhの円錐台を，体積が等しくなるように
    上底に平行な（n-1）個の平面でn等分したとき，n個の円錐台の高さをそれぞれ求めよ。


  43. 円に内接する四角形ABCD について，その内接円から4 つの
    頂点に向かって連結した無限個の四角形の内接円を考える。
    AB＝4 ，BC＝6 ，CD＝5 ，DA＝3 のとき，これらすべての円
    の面積和を求めよ。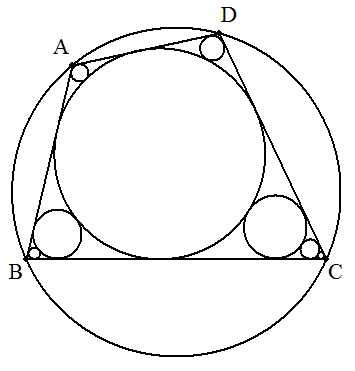

  44. (x+1)(x+2)(x+3)･･･(x+n)を展開したとき，次の項の係数を求めよ。
    (1)　xn-2
    (2)　xn-3
    (3)　xn-4

  45. 3次関数y＝-x3+3x(a≦x≦a+1)の最大値をM(a)，最小値をm(a)とおくとき，次の問いに答えよ。
    (1)　M(a)，m(a)をそれぞれ求めよ。
    (2)　M(a)－m(a)＝kを満たすaの値の個数を求めよ。

  46. 次の式を簡単にせよ。
    (1)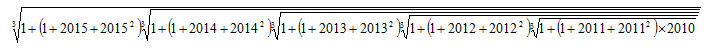　
    (2)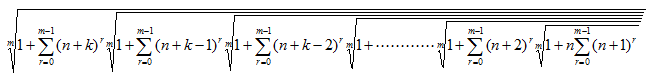　
    ただし，k，m，nは正の整数で，m≧2とする。

  47. 三角形OABのOA上にn個の点A1，A2，･･･，AnをOに近いところから，
    OB上にn個の点B1，B2，･･･，BnをOに近いところから，
    ⊿OA1B1
    ＝⊿A1B1B2＝⊿A1A2B2
    ＝⊿A2B2B3＝⊿A2A3B3
    ＝⊿A3B3B4＝⊿A3A4B4
    ･････････････････････
    ＝⊿AnBnB＝⊿AnAB
    となるようにとる。
    OA＝a，OB＝bのとき，
    (1)　OAk，OBk（k＝1，2，3，･･･，n）を求めよ。
    (2)　AkAk+1，BkBk+1（k＝1，2，3，･･･，n）を求めよ。
    (3)　AkAk+1×BkBk+1（k＝1，2，3，･･･，n）を求めよ。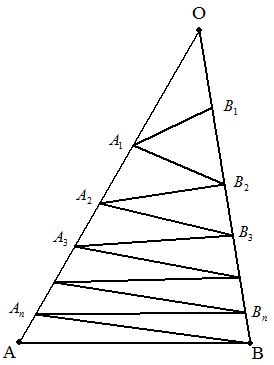

  48. 13，23，33，･･･，n3の中から1個m3（1≦m≦n）を除き，平均をとると75145になった。
    除いた数m3を求めよ。

  49. 1から2n2までの数を，次のように横に2n列，縦にn行並べた。囲まれた部分に入っている数の総和を求めよ。


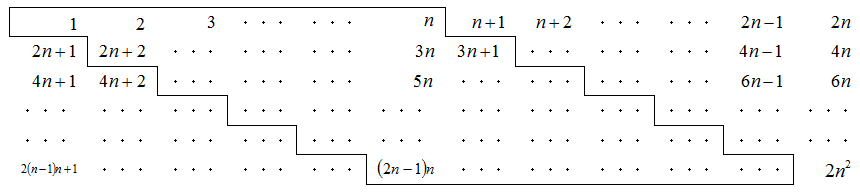
  50. (1)12，22，32，･･･，n2の中から1個m2（1≦m≦n）を除き，平均をとるとm2になった。
    このようなn，mを1組求めよ。
    (2)13，23，33，･･･，n3の中から1個m3（1≦m≦n）を除き，平均をとるとm3になった。
    このようなn，mを1組求めよ。