趣味の数学問題集・Ｂ問題

■趣味の数学問題集・Ｂ問題

1辺aの正方形ABCDの頂点B，Cを中心とし，半径aの円を
正方形内に描き，その各弧上に点G，Hをもち，かつ，
BCの中点に点Eをもつ正五角形EFGHIを描く。
このとき，GHに接し，かつ2つの弧に内接する右図の円Jの
半径をaを用いて表せ。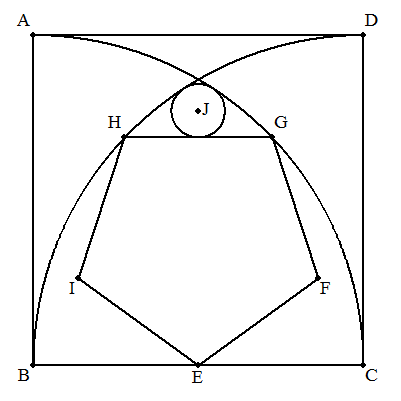

1辺の長さがaである正方形ABCDの辺BC，CD上
に点E，Fを∠AEF＝90°となるようにとる。三角形
ECFの面積が最大になるとき，ECの長さを求めよ。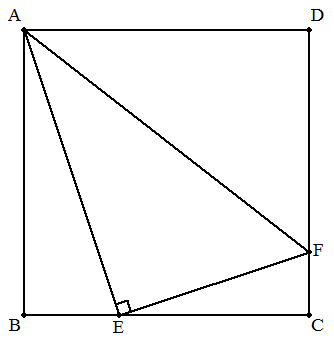
(5+1)(5²+1)(5⁴+1)(5⁸+1)(5¹⁶+1)･･･(5⁵¹²+1)の桁数を求めよ。
ただし，log₁₀2＝0.3010とする。

AB＝5，BC＝7，CA＝3である三角形ABCの外部に点Pを
∠APB＝45°，∠APC＝30°となるようにとる。
このような点は，右図よりP，Qの2通り考えられる。
(1) AP，BP，CPを求めよ。
(2) AQ，BQ，CQを求めよ。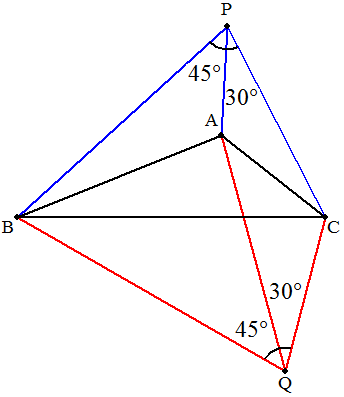

1辺の長さがaである正2n角形A₁A₂･･･A_2nについて
A₁A₂の中点をB₁
A_nA_n+1の中点をB₂
A_n+1A_n+2の中点をB₃
A_2nA₁の中点をB₄
B₁A_n+2とA_nB₄の交点をP
A₂B₃とA_nB₄の交点をQ
A₂B₃とB₂A_2nの交点をR
B₂A_2nとB₁A_n+2の交点をSとする。
(1)　四角形A₁B₁PB₄の面積を求めよ。
(2)　四角形PQRSの面積を求めよ。
(3)　四角形B₁A₂QPの面積を求めよ。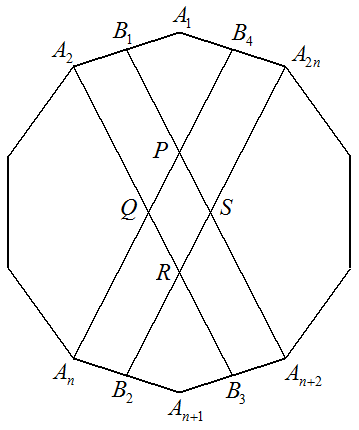

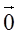でない2つのベクトル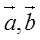について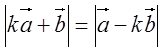，であるとき，次の問に答よ。

(1)　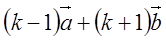と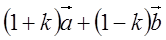のなす角を求めよ。

(2)　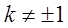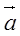，を定ベクトルとする。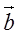はどのような図形上にあるか。

右図の3つの同心円の半径は，外側から順に13，10，7である。
同心円周上に1点ずつ点A，B，Cをとり，正三角形ABCをつくる。
正三角形の1辺を求めよ。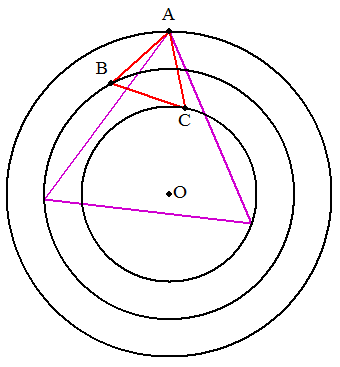

3つの平行線l₁，l₂，l₃ が図のように与えられている。
それぞれの平行線上に1点ずつA，B，Cをとり，
正三角形ABCをつくる。
直線 l₁，l₂ の距離を d₁，直線 l₂，l₃ の距離を d₂と
するとき，正三角形の1辺を求めよ。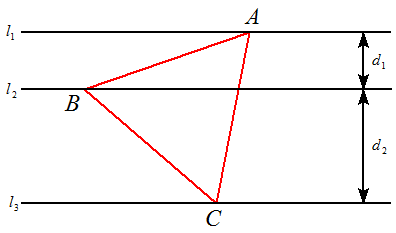

扇形OAB内に2つの正方形を内接させる。
正方形CDEFは，DE∥ABで，
正方形GHIJの辺GHはOA上にある。
2つの正方形の面積が等しくなるとき，
扇形の中心角（0<∠AOB<π/2 ）を求めよ。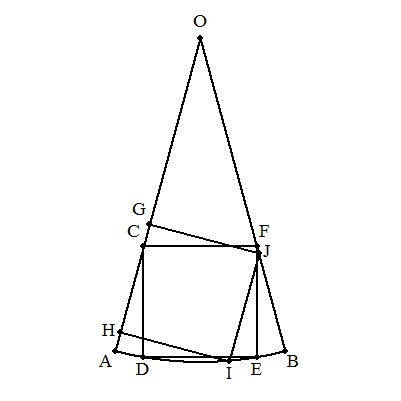

半径1，中心角θ（tan(θ/4)＝1/7）の扇形OAB内に
図のように等円P，Qを内接させ，さらに円Rを円P，Q
に外接させOA，OBに内接させる。
このとき，
(1)　円Pの半径を求めよ。
(2)　円Rの半径を求めよ。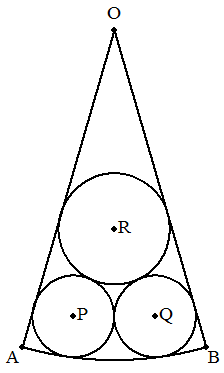

AB＝3，BC＝4，CD＝8である四角形ABCDの
外接円Oについて，頂点A，Cにおける接線の
交点をPとす。3点P，B，Dが一直線上にある
とき，
(1)　DAを求めよ。
(2)　円の半径を求めよ。
(3)　PAを求めよ。
(4)　PBを求めよ。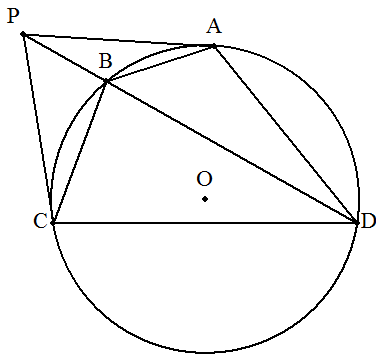

CA＝b，AB＝cである△ABCの∠Aの二等分線とBCとの
交点をDとする。次の場合について，ADを求めよ。
(1)　∠BAC＝A
(2)　BC＝a
(3)　BD＝a₁，DC＝a₂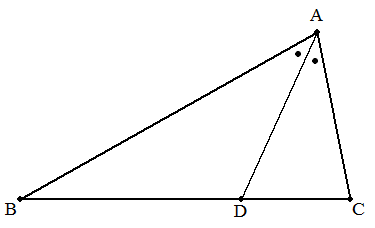
半径rの円に正五角形ABCDEが内接して
いる。円周上の任意の点をPとすると，
PA²+PB²+PC²+PD²+PE²=10r²となることを
証明せよ。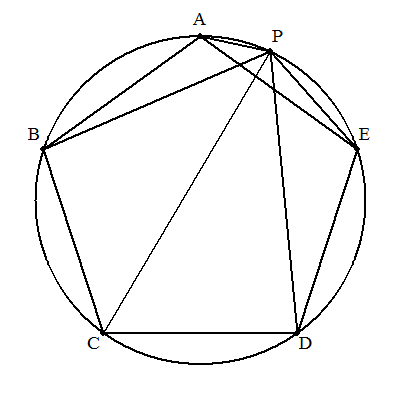
半径rの円に正n角形A₁A₂A₃･･･A_nが内接している。円周上の任意の点をPとすると，
PA₁²+PA₂²+PA₃²+･･･+PA_n²=2nr²となることを証明せよ。

1辺の長さが1である正三角形ABCの
BC上に点Dをとり，CA上に点Eを，
BD＝CEとなるようにとる。
また，点DからABに下ろした垂線の
足をFとする。
点DがBからCまで動くとき，△DEF
の外心Pの軌跡を求めよ。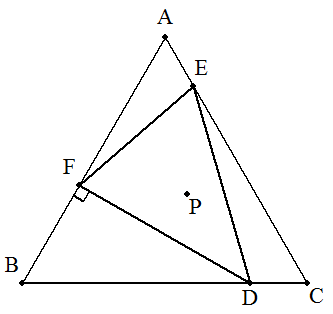

△ABCの辺BCの中点をDとする。また，AC，AB
上にそれぞれ点E，Gを，△ABC内に点Fをとると，
四角形DEFGが正方形になるという。
BC＝3，CA＝4，∠BCA＝90°のとき，正方形
の1辺の長さを求めよ。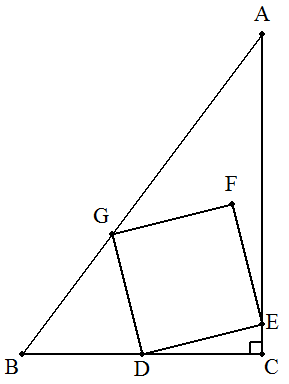

△ABCの辺BCの中点をDとする。また，AC，AB
上にそれぞれ点E，Gを，△ABC内に点Fをとると，
四角形DEFGが正方形になるという。
BC＝13，CA＝14，AB＝15のとき，AFを求めよ。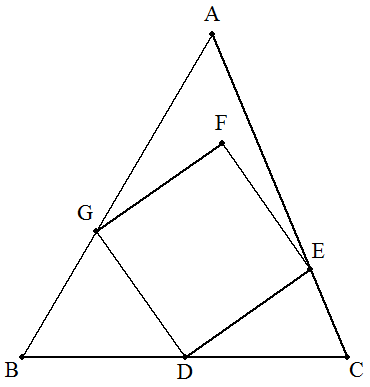

あるn次方程式のn個の解の1乗，2乗，･･･，n乗の和を，それぞれu₁，u₂，･･･，u_nとする。
(1)　n＝3のとき，この方程式を求めよ。
(2)　n＝4のとき，この方程式を求めよ。
(3)　n＝5のとき，この方程式を求めよ。
(4)　n＝6のとき，この方程式を求めよ。
(1＋x＋x²)²⁰¹⁵＝a₀＋a₁x＋a₂x²＋･･･＋a₄₀₃₀x⁴⁰³⁰とおくとき，
(1)　a₂の値を求めよ。
(2)　a₁＋a₄＋a₇＋･･･＋a₄₀₃₀の一の位を求めよ。
(3)　a₁＋a₄＋a₇＋･･･＋a₄₀₃₀の桁数を求めよ。ただし，log₁₀3＝0.4771とする。
nが3の倍数でない奇数のとき，(x＋y)ⁿ－(xⁿ＋yⁿ)は，x²＋xy＋y²で割り切れることを証明せよ。

数列{a_n}の初項から第n項までの和をS_nとおく。

(1)	数列{a_n}は等差数列である。S_3nをS_n，S_2nを用いて表せ。
(2)	数列{a_n}は公比が1でない等比数列である。S_3nをS_n，S_2nを用いて表せ。
(3)	(2)で，S_knをS_n，S_2nを用いて表せ。ただし，k≧3とする。

ある正の整数を3等分し，その商に端数があればそれを捨て，次にこの得たる整数を3等分し，
その商に端数があればそれを捨て，この計算をn回したとき，最後に1となった。
このようになる整数の最大と最小を求めよ。
同一平面上にない4点O(0，0，0)，A(x₁，y₁，z₁)，B(x₂，y₂，z₂)，C(x₃，y₃，z₃)について，
四面体O-ABCの体積を求めよ。
空間座標における4点O(0，0，0)，A(-t，t²，t³)，B(t²，-t³，t)，C(t³，t，-t²) について，
-1<t<0 における四角錐O-ABCの体積の最大値を求めよ。
tan46°=1.0355，tan60°=1.7321，tan74°=3.4874を用いて，
tan46°tan60°tan74°の値を小数第4位まで求めよ。
(sin1°+sin2°+sin3°+･･･+sin90°)(cos1°+cos2°+cos3°+･･･+cos90°)の値を
cos1°を用いて簡単に表せ。
数列{a_n}：2，5，8，11，･･･について
(1)　等差数列のとき，一般項を求めよ。
(2)　等差数列でないとき，一般項を求めよ。
西暦2015年は，平成27年である。
nが2以上の整数であるとき，
2数 ⁿ√27＋ⁿ√2016，ⁿ√28＋ⁿ√2015 のうち，大きい方を答よ。
いくつかの連続する自然数の2乗の和が2018になるとき，
連続する自然数の始めの数と終わりの数を求めよ。
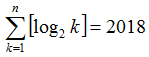となる正の整数nの値を求めよ。

ただし，[x]はxを超えない最大の整数を表す（ガウス記号）。
次の表について，以下の問いに答えよ。

　 1列 2列 3列 4列 5列 6列 7列 8列 9列 10列 11列･･･

1行 1 3 9 7 5 13 21 11 34 29 　･･･

2行 2 6 6 3 11 18 10 21 23 30 　･･･

3行 3 5 2 7 15 9 13 19 27 13 　･･･

4行 4 1 5 12 8 8 17 24 12 55 　･･･

(1)　規則を見つけて，11列目の空欄を埋めよ。
(2)　2018列の2行目にくる数を求めよ。
(3)　表の中に233は何回現れるか。
数列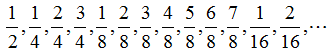について

(1)　初項から第2018項までの和を求めよ。
(2)　初項からの和が2018を超えるのは第何項からか。
次の群数列について，自然数nは第何群の第何項か求めよ。
(1)　1｜2，3｜4，5，6｜7，8，9，10｜11，･･･
　第k群にはk項あるものとする。

(2)　1｜2，3｜4，5，6，7｜8，9，10，11，12，13，14，15｜16，･･･
　第k群には2^k-1項あるものとする。
次の群数列について，奇数nは第何群の第何項か求めよ。
(1)　1｜3，5｜7，9，11｜13，15，17，19｜21，･･･
　第k群にはk項あるものとする。

(2)　1｜3，5｜7，9，11，13｜15，17，19，21，23，25，27，29｜31，･･･
　第k群には2^k-1項あるものとする。
四角形ABCDにおいて，AD＝BC，∠ADB＝24°，
∠CBD＝12°，∠CDB＝18°のとき，
(1)　∠ABD＝x の大きさを求めよ。
(2)　CA＝CDを証明せよ。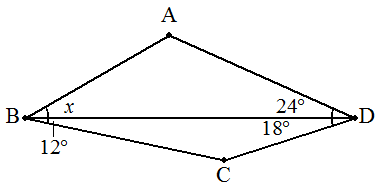
a_n=1-2/(n³+1)に対して，P_n=a₂a₃･･･a_n（n=2，3，･･･）とおく。
(1)　P_n>2/3を示せ。
(2)　P_n<0.667を満たす最小のnの値を求めよ。

	1列	2列	3列	4列	5列	6列	7列	8列	9列	10列	11列	･･･
1行	1	3	9	7	5	13	21	11	34	29		･･･
2行	2	6	6	3	11	18	10	21	23	30		･･･
3行	3	5	2	7	15	9	13	19	27	13		･･･
4行	4	1	5	12	8	8	17	24	12	55		･･･

次の恒等式を証明せよ。
_rC_r+_r+1C_r+_r+2C_r+･･･+_r+iC_r=_r+i+1C_r+1
ただし，r=0，1，2，･･･，i=1，2，3，･･･とする。

（例）r=3，i=4のとき，₃C₃+₄C₃+₅C₃+₆C₃+₇C₃=₈C₄
右図でホッケーのスティックの柄の部分の数の
和が刃の部分の数に等しくなる。
（ホッケーのスティック恒等式）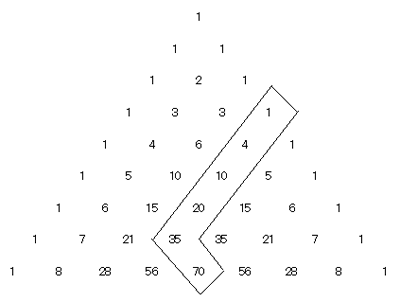

△ABCと点Dについて，∠BDC＝α，∠CDA＝β，
∠ADB＝γとおくと，
cos²α+cos²β+cos²γ-2cosαcosβcosγ=1
が成り立つことを証明せよ。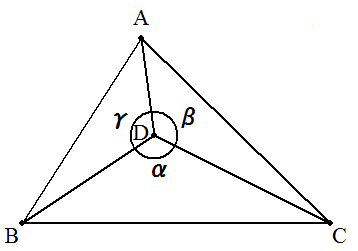
4辺の長さが与えられた四角形の面積は，四角形が
円に内接するとき最大となることを証明せよ。
座標空間において，平面α：ax+by+cz+d=0 と点P(x₁,y₁,z₁)について，
(1)　点Pと平面αに関して対称な点Qの座標を求めよ。
(2)　点Pと平面αとの距離hを求めよ。
四角形ABCDの内接円，外接円の中心をそれぞれI，Oとする。
AB＝4，BC＝6，CD＝5，DA＝3のとき，IOを求めよ。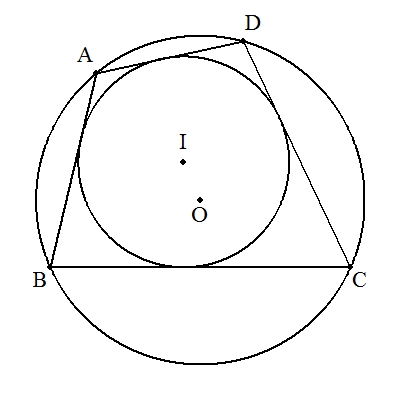
2定点A，Bからの距離の比がm:n（m≠n）である点Pの軌跡を，次の場合にそれぞれ求めよ。
(1)　平面の場合　A(x₁,y₁) ，B(x₂,y₂)
(2)　空間の場合　A(x₁,y₁,z₁) ，B(x₂,y₂,z₂)
数列：{a_(1)n}：1，2，3，4，5，6，7，8，9，10，･･･について
隣接する2項の和で新たな数列
{a_(2)n}：3，5，7，9，11，13，15，17，19，･･･をつくる。
さらに，この数列の隣接する2項の和で新たな数列
{a_(3)n}：8，12，16，20，24，28，32，36，･･･をつくる。
このように、次々と数列
{a_(4)n}：20，28，36，44，52，60，68，･･･
{a_(5)n}：48，64，80，96，112，128，･･･
･･････････････････････････････
をつくる。
このとき，
(1)　数列{a_(k)n}の一般項を求めよ。
(2)　2016は何番目の数列の第何項か，すべて求めよ。
x²の係数が1である2次関数 y=f(x) に点（p，q）から2本の接線を引く。
この2つの接線と2次関数によって囲まれる部分の面積が 2/3 のとき，
qをpを用いて表せ。

1辺1の正方形ABCDについて，BCを1：2に内分する点をE，
CDをk：(1-k)に内分する点をFとする。（ただし，0<k<1）
AEとBFの交点をG，四角形CFGEをSとおく。
SをABを軸として1回転してできる立体の体積をV_AB，
ADを軸として1回転してできる立体の体積をV_ADとする。
V_AB＝V_ADのとき，kの値を求めよ。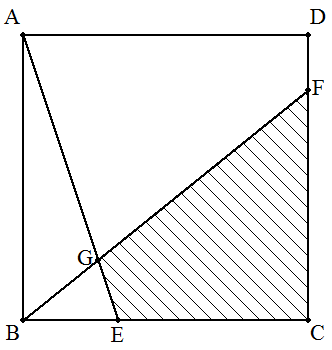

f(x)=ax³+bx²+cx+d，
a=2(p-q)/(β-α)³，b=-3(p-q)(α+β)/(β-α)³，c=6(p-q)αβ/(β-α)³，
d=(pβ³-3pαβ²+3qα²β-qα³)/(β-α)³について，
α<β，p>qのとき，y=f(x)の極値とそのときのxの値を求めよ。
y=(x-α)(x-β)(x-γ)(α<β<γ)とx軸とで囲まれた部分の面積Sを，
β-α=a，γ-β=bを用いて表せ。
a>0とする。
x=(1+1/a)^a+1，y=(1+1/a)^aのとき，x^1/x，y^1/yの大小を比較せよ。
1辺の長さがaである正方形ABCDの辺BC，CD上
に点E，Fを∠AEF＝90°となるようにとる。三角形
ECFの面積が最大になるとき，ECの長さを求めよ。
4分の1円Oの半径を1とするとき，半円A，半円B，円C，
円D，円E，円F，半円G，円Hの半径をそれぞれ求めよ。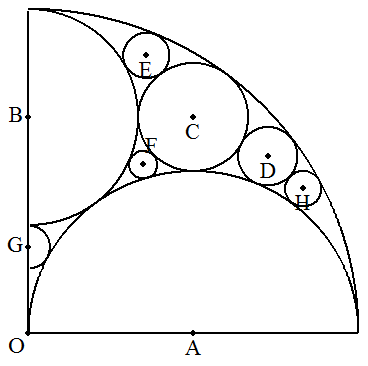