■趣味の数学問題集・Ｂ問題

  1. 円Oに外接する四角形ABCDについて，
    (1)　AB/(OA・OB)＝CD/(OC・OD)
    (2)　AD/(OA・OD)＝BC/(OB・OC)
    が成り立つことを証明せよ。


  2. 四角形ABCDの内接円とAB，BC，CD，DAとの接点をそれぞれE，F，G，Hとする。
    4次方程式x4-10x3+35x2-49x+21＝0は4つの正の解α，β，γ，δをもつことが
    知られている。
    α＝AE，β＝EB，γ＝CG，δ＝GDとおくとき，四角形ABCDの面積を求めよ。


  3. 五角形ABCDEの内接円とAB，BC，CD，DE，EAとの接点をそれぞれF，G，H，I，J
    とする。AF=1，BG=2，CH=3，DI＝4，EJ＝5のとき，五角形ABCDEの面積を求めよ。


  4. 六角形ABCDEFの内接円とAB，BC，CD，DE，EF，FAとの接点をそれぞれG，H，I，
    J，K，Lとする。AG=1，BH=2，CI=3，DJ＝4，EK＝5，FL=6のとき，六角形ABCDEF
    の面積を求めよ。


  5. 七角形ABCDEFGの内接円OとAB，BC，CD，DE，EF，FG，GAとの
    接点をそれぞれH，I，J，K，L，M，Nとする。
    AH=1，BI=2，CJ=3，DK＝4，EL＝5，FM=6，GN＝7のとき，円Oの
    半径rの満たす6次方程式を求めよ。ただし，r6の係数は1とする。


  6. △ABCの重心をGとする。
    ∠GAB＋∠GBC＋∠GCA＝90°のとき，
    △ABCは二等辺三角形となることを証明せよ。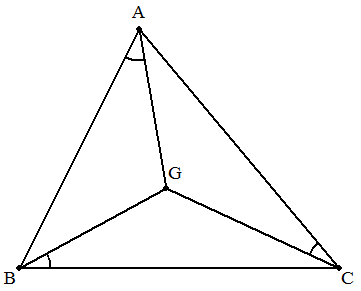


  7. 当たりくじが2017本入っているn本のくじがある。
    次の各々の場合について，nの値を求めよ。
    (1)　2本引いて，少なくとも1本あたりを引く確率が1/2を超えるとき，nの最大値
    (2)　3本引いて，少なくとも1本あたりを引く確率が1/2を超えるとき，nの最大値
    (3)　4本引いて，少なくとも1本あたりを引く確率が1/2を超えるとき，nの最大値


  8. 原点中心，半径1の円に内接する
    正五角形ABCDEの頂点A，C，Eを通る
    放物線y=ax2+bx+cを求めよ。
    ただし，A(1,0)とする。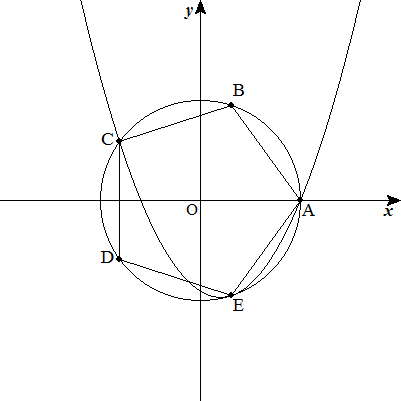



  9. 原点中心，半径1の円に内接する
    正五角形ABCDEの頂点A，B，D，Eを
    通る3次関数y=ax3+bx2+cx+dを求めよ。
    ただし，A(0,1)とする。



  10. 原点中心，半径1の円に内接する
    正七角形ABCDEFGの頂点A，D，F，Gを
    通る放物線y=ax2+bx+cを求めよ。
    ただし，A(1,0)とする。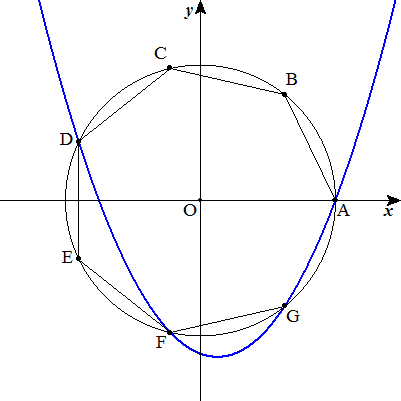



  11. BC＝8，CA＝7，AB＝5である△ABCの
    BC上に点DをBD=1となるようにとる。
    また，DC上に点Eを∠BAD=∠CAEとなる
    ようにとる。このとき，ECを求めよ。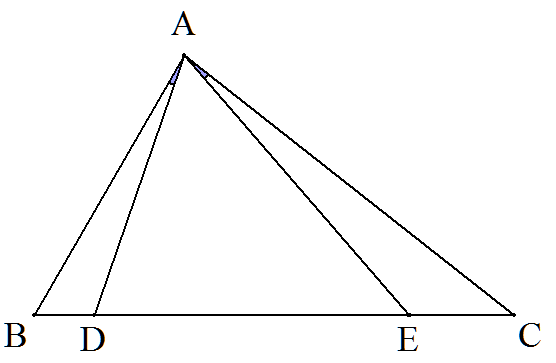



  12. BC＝8，CA＝7，AB＝5である△ABCの
    BC上に点EをAB=AEとなるようにとる。
    また，BE上に点Dを∠CAE=∠BADとなる
    ようにとる。このとき，BDを求めよ。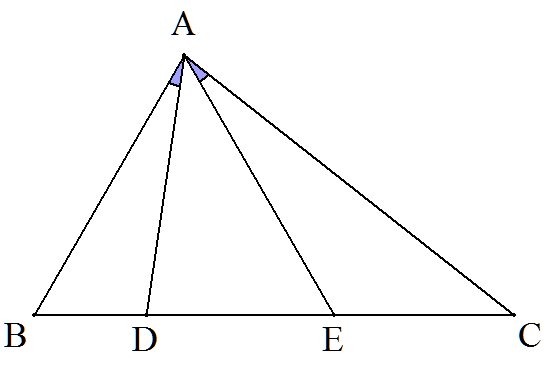



  13. a=1，B=60°，C=45°である△ABCの頂角の
    三等分線の辺に近い2辺ずつの線分の交点を
    図のようにD，E，Fとする。
    このとき，EFをcos5°を用いて表せ。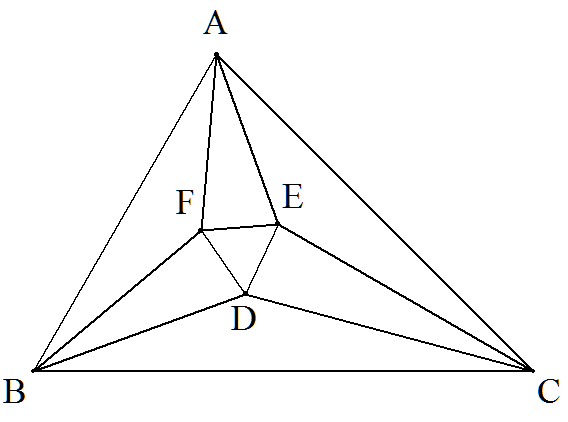



  14. a=1，B=60°，C=45°である△ABCの頂角の外角の
    三等分線の辺に近い2辺ずつの線分の交点を図の
    ようにD，E，Fとする。
    このとき，EFをcos5°を用いて表せ。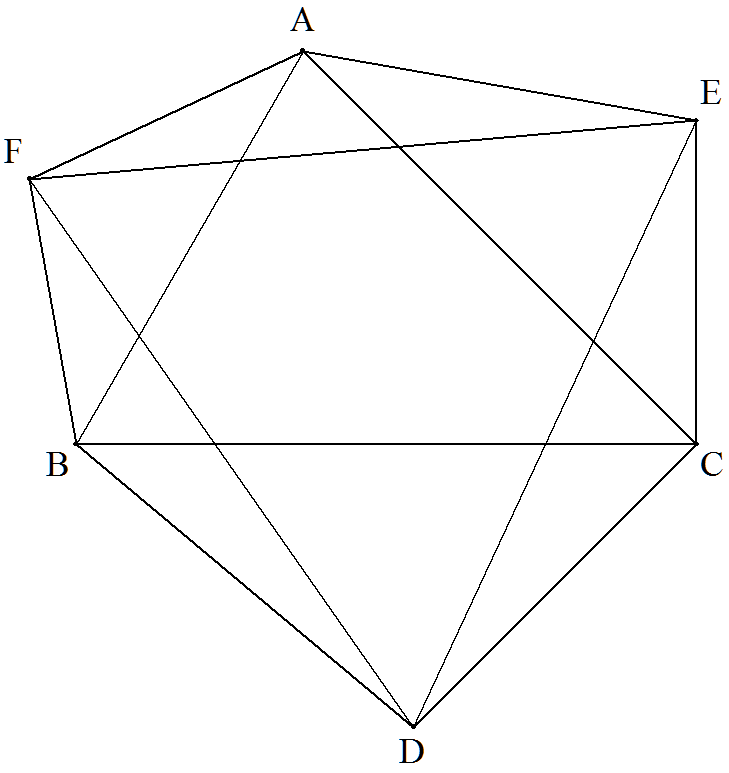



  15. ∠BAC＝A，CA＝b，AB＝cである△ABCの
    ∠BACの二等分線とBCとの交点をD1,
    ∠BAD1の二等分線とBCとの交点をD2,
    ∠BAD2の二等分線とBCとの交点をD3,…，
    と次々にD4，D5，…，Dnをとる。
    次の長さを，A，b，c，nを用いて表せ。
    (1)　ADn
    (2)　BDn



  16. △ABCの∠Aの二等分線とBCの交点をDとする。
    AB上に点Pをとり，3点A，D，Pを通る円とAC
    との交点のうち，Aでない方をQとする。
    AP＝xのとき，AQをa，b，c，xを用いて表せ。



  17. △ABCの∠Aの二等分線とBCの交点をD，AB，ACの
    中点をそれぞれE，Fとし，4点A，D，E，Fを通る円が
    存在するとき，
    (1)　(b+c)/aの値を求めよ。
    (2)　△ABCの面積をb，cを用いて表せ。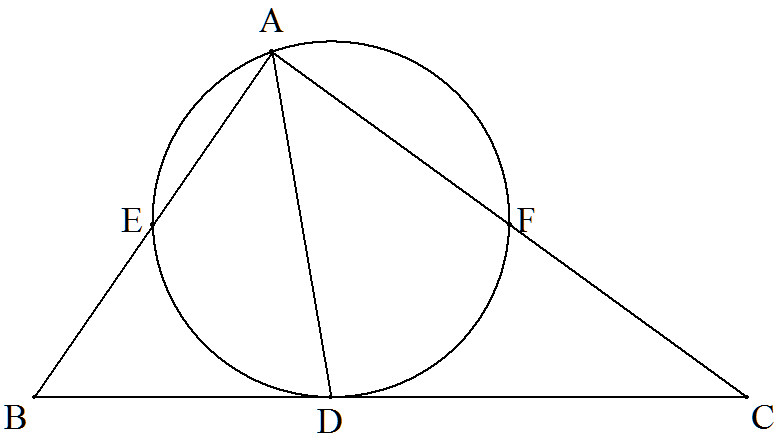



  18. △ABCの最大角AからBCに下した垂線の足をD，
    ∠Bの二等分線とCAの交点をＥ，ABの中点を
    Fとし，CF，ADの交点をP，AD，BEの交点をQ，
    BE，CFの交点をRとする。
    このとき，△PQR/△ABCの値を求めよ。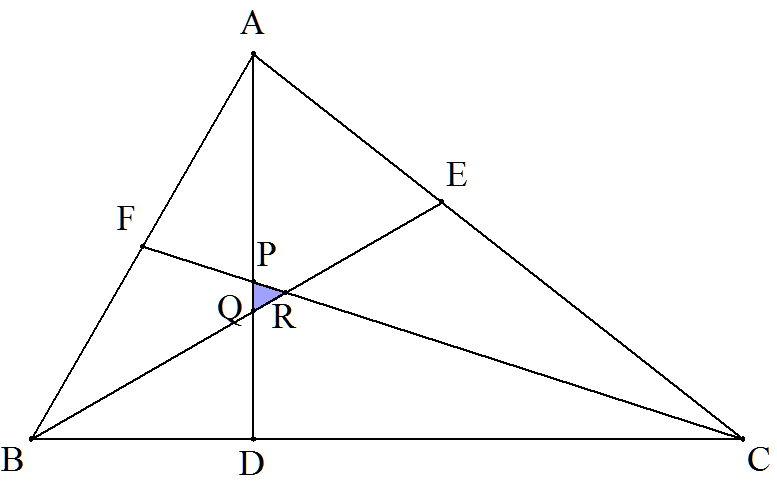



  19. △ABCの辺BC，CA，AB上にそれぞれ点D，E，Fを，
    ∠DAB＝∠EBC=∠FCA＝θとなるようにとる。
    CF，ADの交点をP，AD，BEの交点をQ，BE，CFの
    交点をRとするとき，△PQR/△ABCの値を，θ，A，
    B，Cを用いて表せ。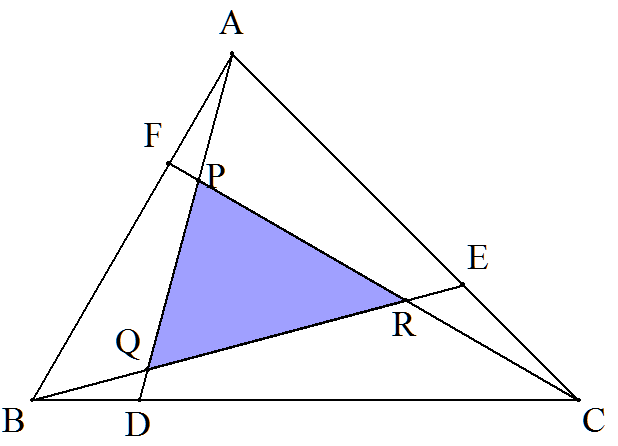



  20. 正27角形A1A2A3…A27の面積が1のとき，
    台形A5A6A23A24の面積を求めよ。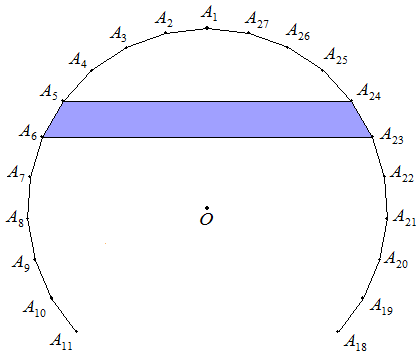



  21. 正(6m+3)角形A1A2…A6m+3の面積をSとするとき，
    台形Am+1Am+2A5m+3A5m+4の面積を求めよ。



  22. BC=a，CA=b，AB=cである△ABCの外心を原点に，
    Aのy座標は正とし，BCをx軸に平行におくとき，
    A，B，Cの座標をa，b，c，S（＝△ABC）を用いて
    それぞれ求めよ。



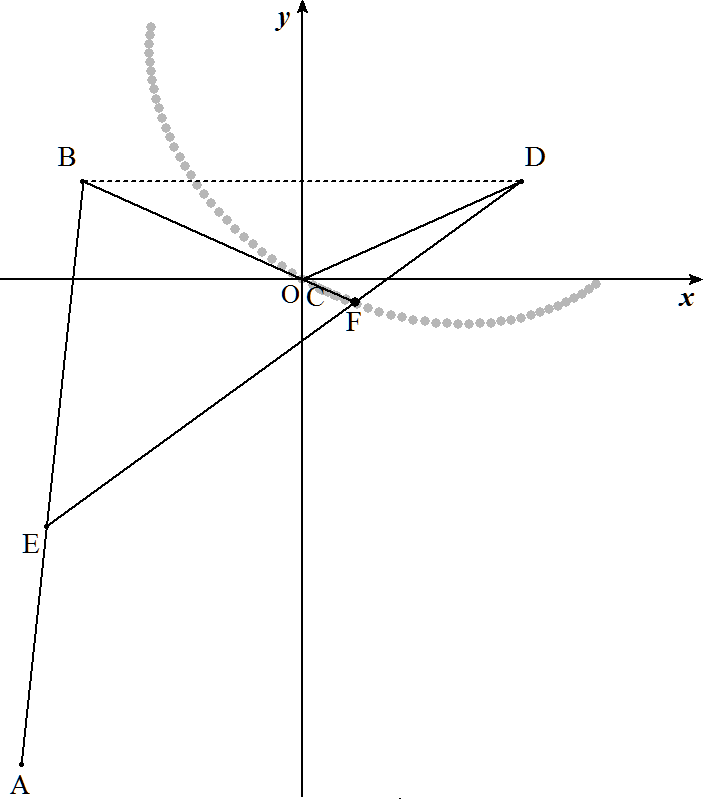
  23. 右の上図は，
    AB=DE，AE=BC=CD，
    ∠AED=∠BCDを満たしている。
    DEと直線BCの交点をFとする。
    (1)　∠BFEを求めよ。
    (2)　下図のように，
    　Cを原点，BDをx軸に平行におき，∠BDC=θとおく。
    　CD=aとおき，θが0°＜θ＜30°（左図），
    　30°＜θ＜60°（右図）の範囲で
    　変化したときの点Fの軌跡は点線のようになる。
    　この軌跡の方程式を求めよ。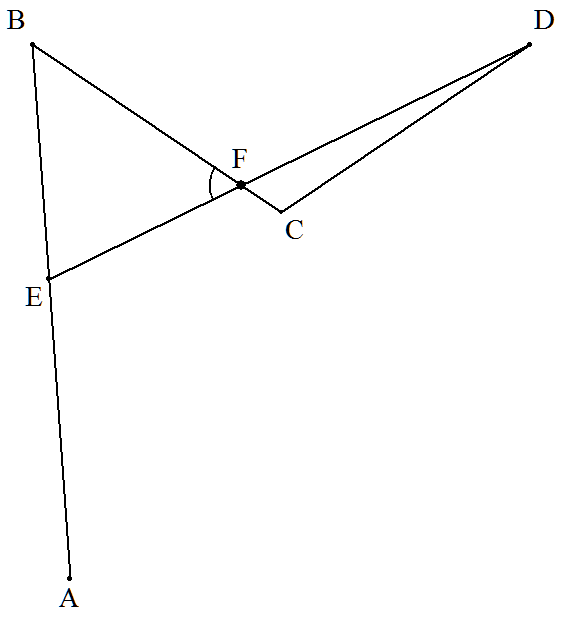



  24. 三角錐O-ABCの6辺が，OA=BC＝a，OB=OC=AB=AC=bであるとき，
    (1)　三角錐の体積Vを求めよ。
    (2)　Vを最大にするaの値をbを用いて表せ。また，そのときの体積を求めよ。



  25. お年玉付き年賀はがきの3等は100枚につき2枚当選となり，お年玉切手シートがもらえる。
    3等が当たる確率を1/2以上にするためには何枚必要か。
    ただし，log102＝0.3010，log107＝0.8451とする。


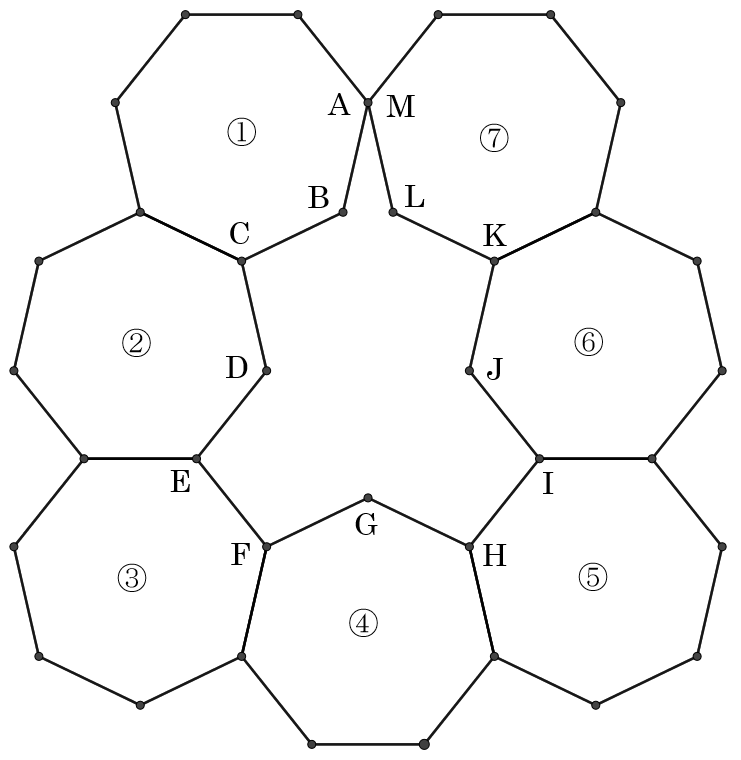
  26. 1辺の長さが1の正七角形①～⑦を図のように①から
    辺を共有させ，次々と連結させ，記号をつける。
    Aは正七角形①の頂点，Mは正七角形⑦の頂点であ
    る。
    さて，12角形ABCDEFGHIJKLの面積を考えようとした
    とき，AとMが一致すれば問題は成立するが，一致し
    なければ問題は成立しない。
    (1)　AとMは一致するかどうか調べよ。
    (2)　AとMが一致するときは，12角形ABCDEFGHIJKL
    　　の面積を，一致しないときは，AMの距離を求めよ。



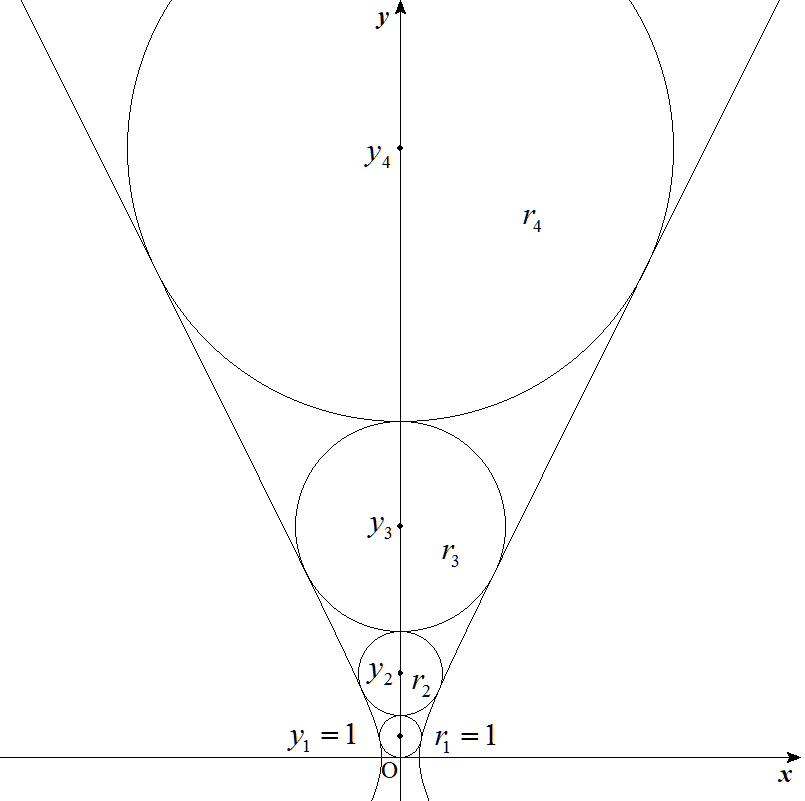
  27. 双曲線(5/4)x2-(5/16)y2=1に接し，中心がy軸上（y＞0）にある円を考える。
    図のように互いに外接し，第1円の中心のy座標y1＝1，半径r1＝1，
    第2円の中心のy座標y2，半径r2，
    第3円の中心のy座標y3，半径r3，…，
    第n円の中心のy座標yn，半径rnとする。
    (1)　第2円の中心のy座標y2および半径r2を求めよ。
    (2)　第3円の中心のy座標y3および半径r3を求めよ。
    (3)　第n円の中心のy座標ynおよび半径rnを求めよ。



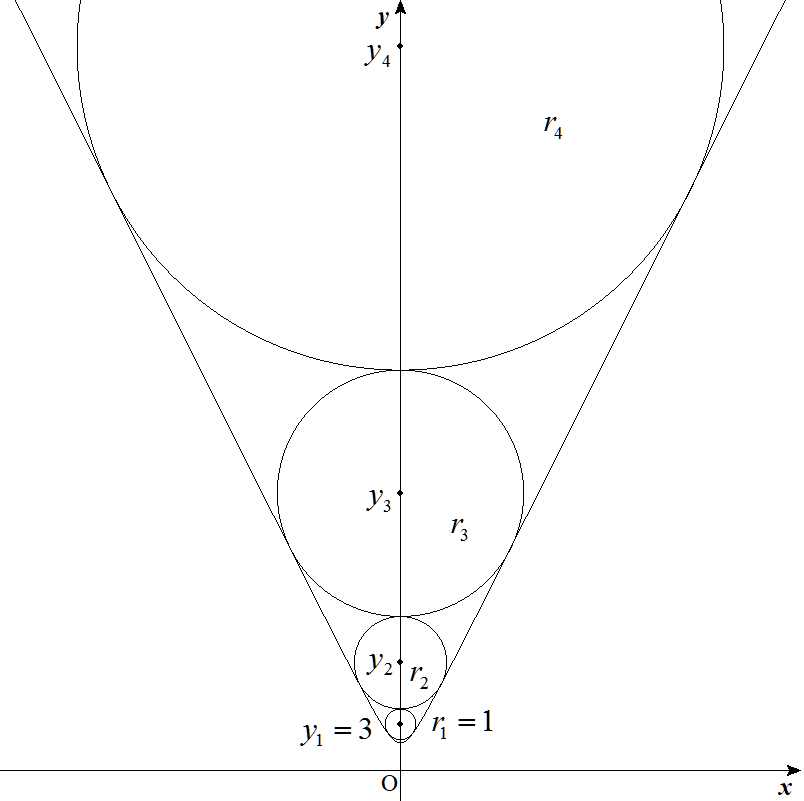
  28. 双曲線(5/4)x2-(5/16)y2=－1（y＞0）に接し，中心がy軸上にある円を考える。
    図のように互いに外接し，第1円の中心のy座標y1＝3，半径r1＝1，
    第2円の中心のy座標y2，半径r2，
    第3円の中心のy座標y3，半径r3，…，
    第n円の中心のy座標yn，半径rnとする。
    (1)　第2円の中心のy座標y2および半径r2を求めよ。
    (2)　第3円の中心のy座標y3および半径r3を求めよ。
    (3)　第n円の中心のy座標ynおよび半径rnを求めよ。



  29. {tan(π/24)+i}12の虚部を求めよ。
    ただし，i は虚数単位で，答は分母を有理化して簡潔な形で求めよ。（累乗は計算しなくてよい。）


  30. 数列 { an }：1，1/3，1/3，5/11，3/5，27/37，29/35，(　)，31/33，…について
    (1)　規則を見つけて，括弧内の数を求めよ。
    (2)　一般項を求めよ。


  31. 数列 { an }：-1/2，-3/4，5/6，7/8，(　)，-11/12，13/14，15/16，(　)，…について
    (1)　規則を見つけて，括弧内の数を求めよ。
    (2)　一般項を求めよ。


  32. 四角形ABCDは円Oに外接している。
    (1)　OA=a，OB=b，OC=c，OD=dのとき，AB/BCの値を求めよ。
    (2)　AB=a，BC=b，CD=c，DA=dのとき，OA/OCの値を求めよ。


  33. 曲線y=ax4+bx3+cx2+dx+eとその曲線に異なる2点で接する
    直線とによって囲まれる図形の面積Sを求めよ。
    ただし，3b2-8ac＞0とする。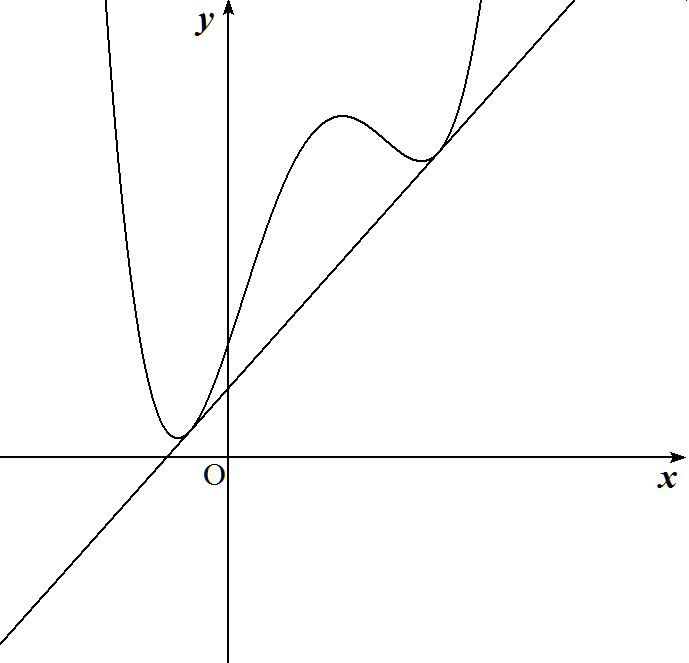




  34. 2つの放物線y=a1x2+b1x+c1，y=a2x2+b2x+c2と
    その共通接線によって囲まれる図形の面積
    の和Sを求めよ。
    ただし，a1＞a2＞0とする。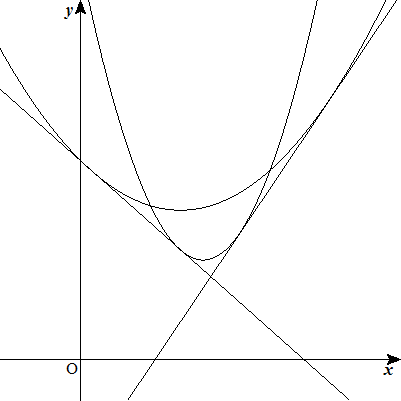




  35. 2つの放物線y=ax2+b1x+c1，y=ax2+b2x+c2と
    その共通接線によって囲まれる図形の面積
    Sを求めよ。
    ただし，b1≠b2とする。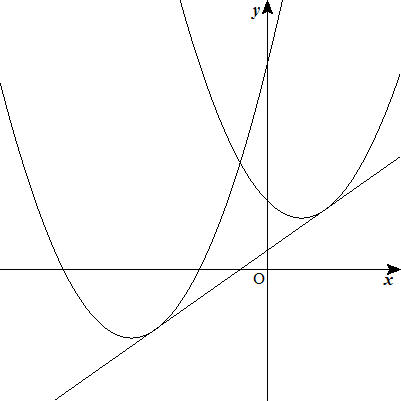




  36. f(a,b,c)=a3+b3+c3-3abcのとき，f(1,2,3)f(4,5,6)=f(a,b,c)を満たす自然数a,b,cの値を1組求めよ。


  37. 正18 角形の対角線の交点のうち，5 本の対角線が1 点で交わる交点の個数を求めよ。


  38. 1辺の長さが1である正五角形ABCDEのCDの中点をMとする。
    AB，BC，AMに接する円Pの半径r1と
    AM，MD，DEに接する円Qの半径r2をそれぞれ求めよ。



  39. 正方形ABCD内の1点Oから各辺に垂線を
    下ろしてその足をA1，B1，C1，D1とする。
    次にOから四角形A1B1C1D1の各辺に垂線を
    下ろしてその足をA2，B2，C2，D2とする。
    このことを4 回くり返せば四角形A4B4C4D4
    はまた正方形となることを，証明せよ。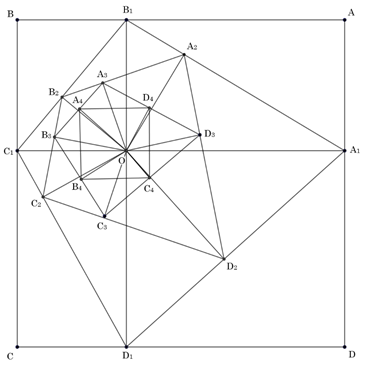



  40. 円に内接する四角形ABCDの各辺を1辺とする正方形を
    四角形の外側につくり，各正方形の対角線の交点を
    図のようにそれぞれP，Q，R，Sとする。
    AB＝4，BC＝6，CD＝5，DA＝3のとき，四角形PQRSの
    面積を求めよ。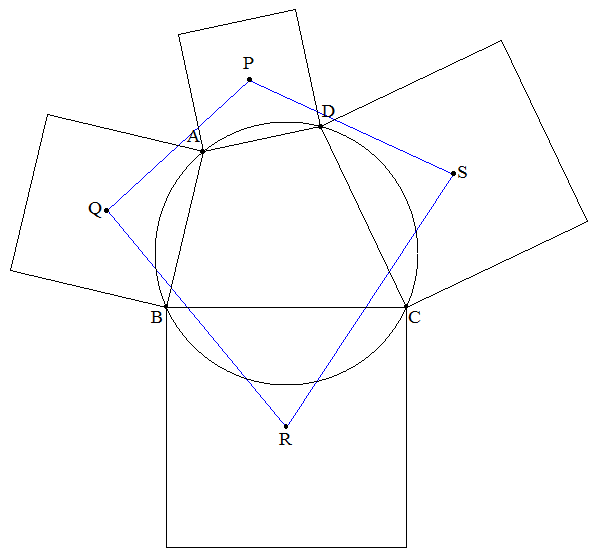



  41. 半径1の円に内接する正n角形A0A1A2･･･An-1について，
    積A0A1・A0A2・･･･・A0An-1の値を求めよ。


  42. 半径1の円に内接する正九角形ABCDEFGHIについて
    積AB・AC・AD・AEの値を求めよ。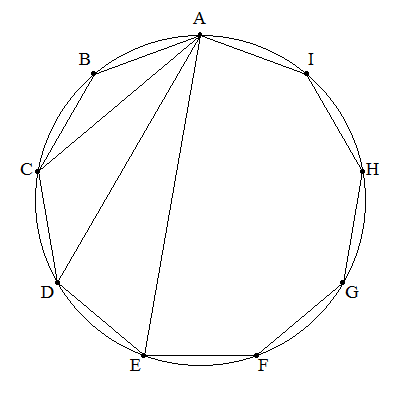



  43. nが自然数のとき，次の等式を証明せよ。



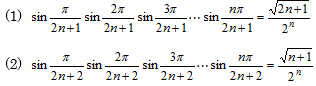
  44. 半径1の円に内接する正七角形ABCDEFGについて，△ABDの面積を求めよ。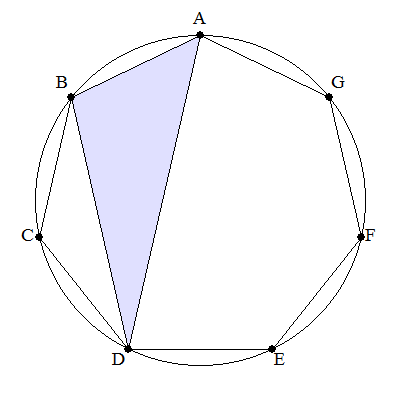



  45. 自然数を次のように表に記入し，m行n列目の数を(m,n)で表す。
    例えば，(5,2)=18である。
    (1)　(m,n)=25を満たす(m,n)を求めよ。
    (2)　(20,19)を求めよ。
    (3)　(m,n)=2019を満たす(m,n)を求めよ。



  46. 実数a，b，cは，a＜b＜c，a+b+c=9，ab+bc+ca=15を満たしている。
    (1)　abcのとり得る値の範囲を求めよ。
    (2)　a，b，cの値の範囲をそれぞれ求めよ。
    (3)　与えられた条件を満たす整数a，b，cの値を求めよ。


  47. 実数a，b，c，dは，a＜b＜c＜d，a+b+c+d=12，ab+ac+ad+bc+bd+cd=46，abc+abd+acd+bcd=60を満たしている。
    b，cが整数のとき，a，b，c，dの値をそれぞれ求めよ。


  48. 次を証明せよ。
    1/(1･2)+1/(3･4)+1/(5･6)+･･･＜3/4


  49. 半径1の円に内接する正七角形ABCDEFGについて，AB=a，AC=b，AD=cとおくとき，(b2-a2)(c2-a2)(c2-b2)の値を求めよ。


  50. 半径1の円に内接する正九角形ABCDEFGHIについて，AB=a，AC=b，AD=c，AE=d，(b2-a2)(c2-a2)=α，(d2-a2)(d2-c2)=βとおくとき，
    (1)　α=βを示せ。
    (2)　αの値を求めよ。