■趣味の数学問題集・Ｂ問題

  1. 四角形ABCDの外側に，図のように各辺を底辺とする相似な
    二等辺三角形PAD，QBA，RCB，SDCをつくる。
    ∠PAD＝θとおくとき，次の場合におけるθの値を求めよ。
    (1)　PR⊥QS
    (2)　PR＝QS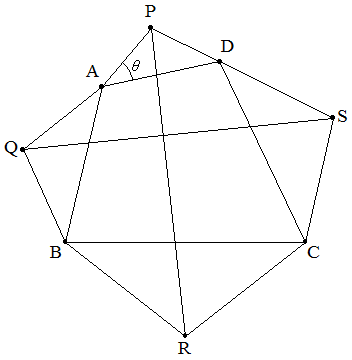



  2. nを自然数とする。
    1辺nの正六角形ABCDEFの各辺をn等分して図のように各辺に
    平行な直線を引いて分割する。
    このとき大小合わせてすべての正六角形の個数を求めよ。



  3. 半径の等しい3つの円が図のように放物線y=ax2（a＞0）に接している。
    円の半径を求めよ。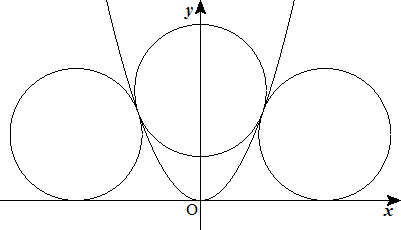



  4. 半径の等しい3つの円が図のように楕円x2/a2+y2/b2=1（a＜b）に接している。
    円の半径を求めよ。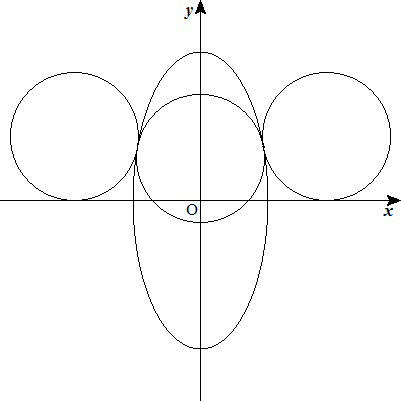



  5. 半径の等しい3つの円が図のように双曲線x2/a2-y2/b2=-1
    （y≧0，√2＜b/a＜√3）に接している。
    円の半径を求めよ。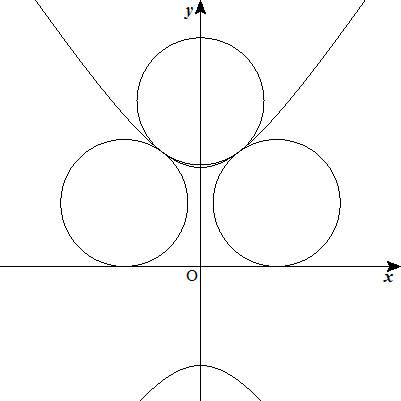



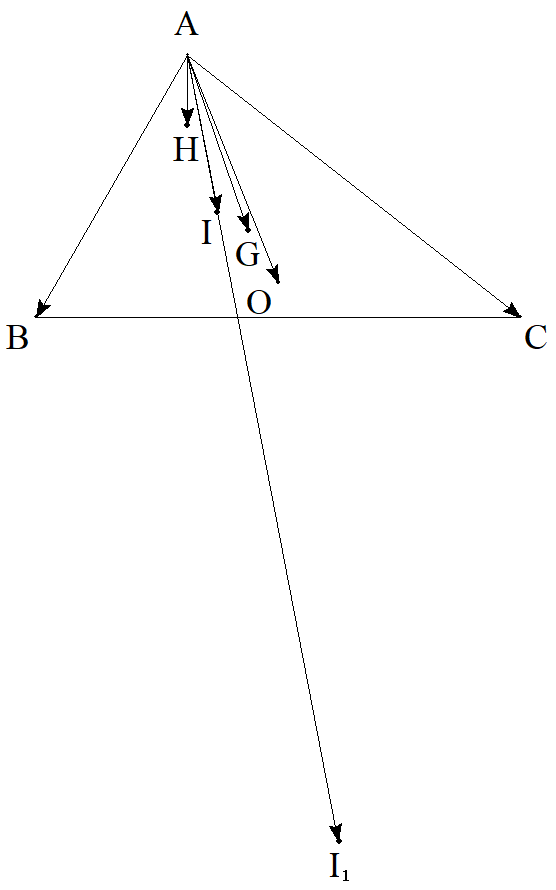
  6. △ABCの3つの傍心をI1，I2，I3とする。
    △I1I2I3の面積を求めよ。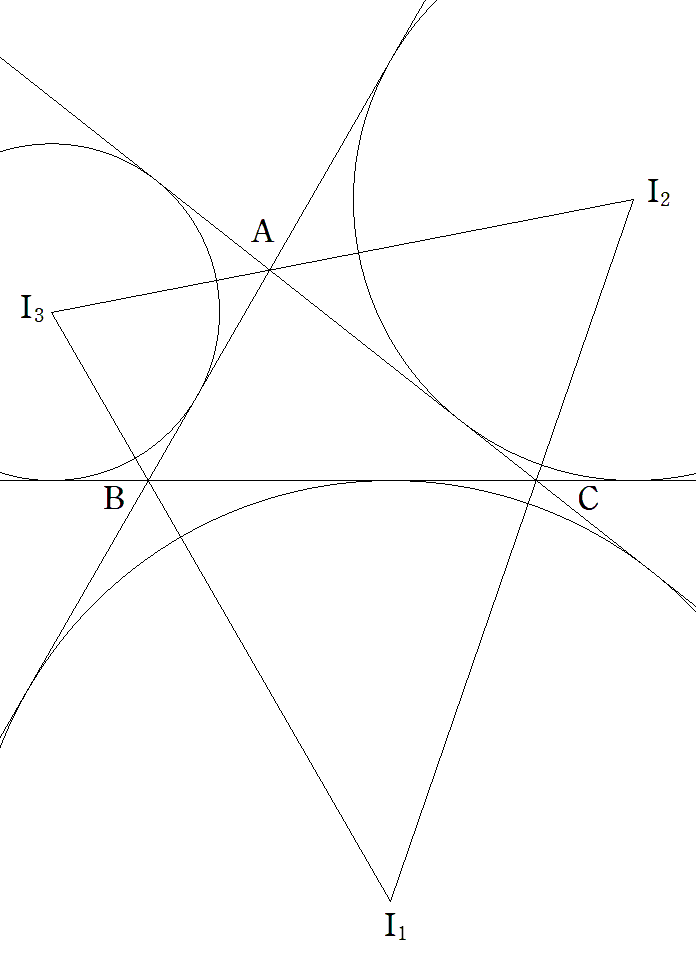



  7. 半径の等しい3つの円が図のように双曲線x2/a2-y2/b2=-1
    （y≧0，√2＜b/a＜√3）に接している。
    b/aの値を求めよ。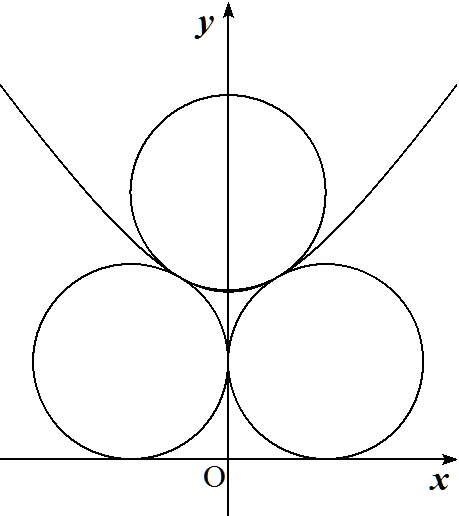



  8. 1辺の長さが1である正三角形内に図のように1つの甲円と3つの乙円が描かれている。
    3つの乙円の面積の和が甲円の面積に等しいとき，甲円の半径を求めよ。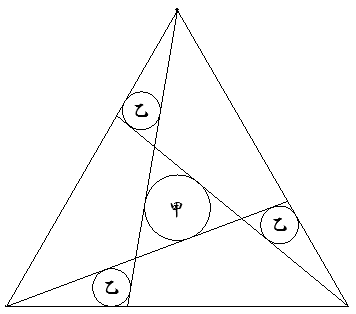






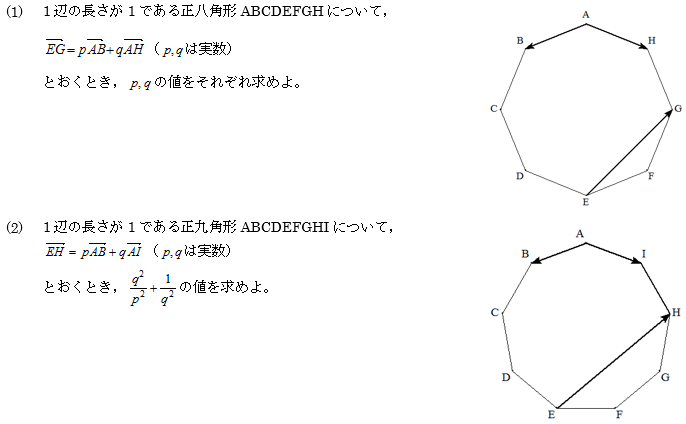
  10. ∠A＝90°である△ABCの内部に半径の等しい2つの円P，Qが，図のように
    BCに接し，円PはABに，円QはCAに接している。円の中心P，QからBCに
    下した垂線の足をそれぞれD，Eとする。
    BD＝p，CE＝qのとき，△ABCの面積を求めよ。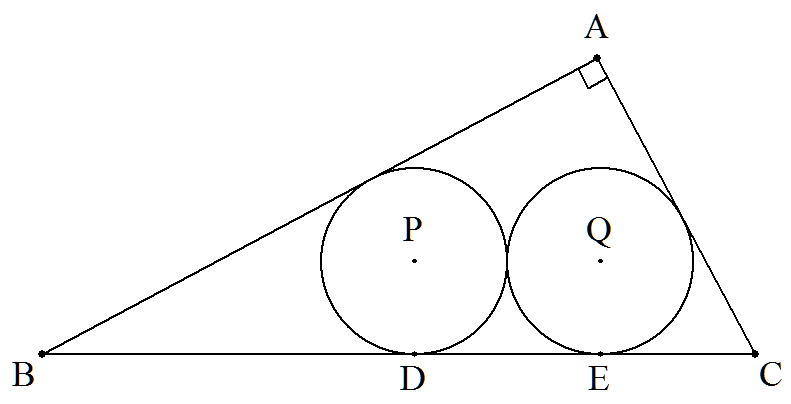



  11. ∠A＝90°である△ABCの内部にn個の等円O1，O2，･･･，Onが，
    図のように互いに外接し，辺に接している。円O1の接点DとBの
    距離をp，円Onの接点EとCの距離をqとするとき，△ABCの面積
    を求めよ。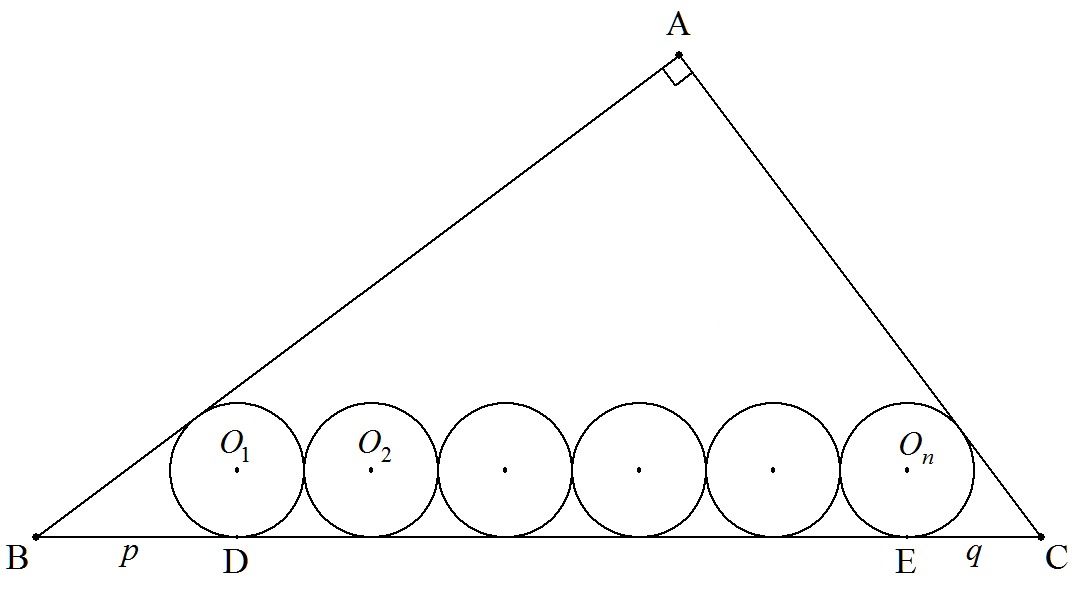



  12. AB＝5，BC＝8，CD＝3，DA＝5，∠ABC＝60°である四角形ABCDについて，
    ABを1：9に内分する点をPとする。BC，CD，DA上にそれぞれ点Q，R，Sをとり，
    PQ＋QR＋RS+SPの最小値を求めよ。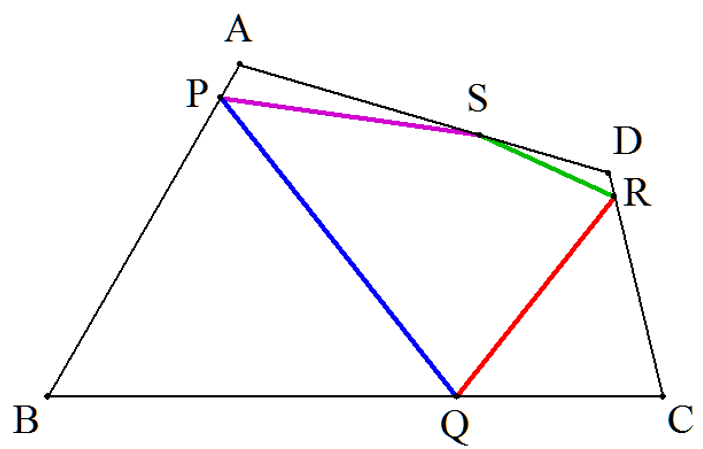



  13. 円Oに外接する四角形ABCDについて，OA＝3，OB＝5，OC＝6，OD＝4のとき，
    次を求めよ。
    (1)　AB：CD
    (2)　AB：BC
    (3)　AB：BC：CD：DA
    (4)　円の半径
    (5)　AB，BC，CD，DA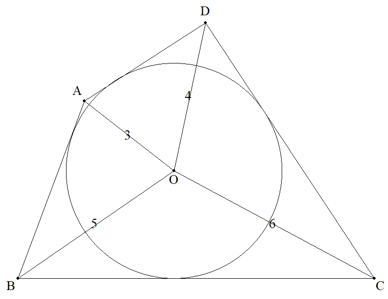



  14. BC＝7，CA＝8，AB＝9である△ABCの内接円の中心（半径）をI（r），
    この円と共有点をもたないCA，ACに接する円の中心（半径）をJ（r'）
    とする。2円の共通内接線とCA，ABとの交点をそれぞれD，Eとする。
    DE＝r＋r'のとき，r'を求めよ。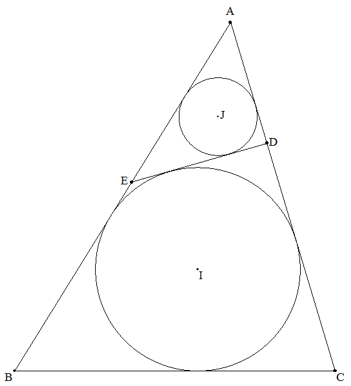



  15. 2点A()，B()に対して，
    ABをm：nに内分する点と外分する点の中点をM1，
    ABをm2：n2に内分する点をN1，M1N1の中点をM2，
    ABをm4：n4に内分する点をN2，M2N2の中点をM3，
    ABをm8：n8に内分する点をN3，M3N3の中点をM4，…
    とMK，NKを定義していくとき，MKの位置ベクトルを求めよ。


  16. 面積Sの△ABCの外接円の半径がRのとき，次の式の値を求めよ。
    (1)　sin3Asin(B-C)+sin3Bsin(C-A)+sin3Csin(A-B)
    (2)　sin3Acos(B-C)+sin3Bcos(C-A)+sin3Ccos(A-B)

    (3)　acosA+bcosB+ccosC


  17. 3次曲線y=ax3+bx2+cx+d…①と点T1(t，t(t))について，
    T1における①の接線l1と①の共有点のうち，T1でない
    方をT2とする。
    T2における①の接線l2と①の共有点のうち，T2でない
    方をT3とする。
    このように，l3，T4，l4，…を定義していく。
    (1)　△TnTn+1Tn+2＝Snとおくとき，Sn+1/Snの値を求めよ。
    (2)　接線ln，ln+1，ln+2で囲まれる三角形の面積をLnと
    おくとき，Ln+1/Lnの値を求めよ。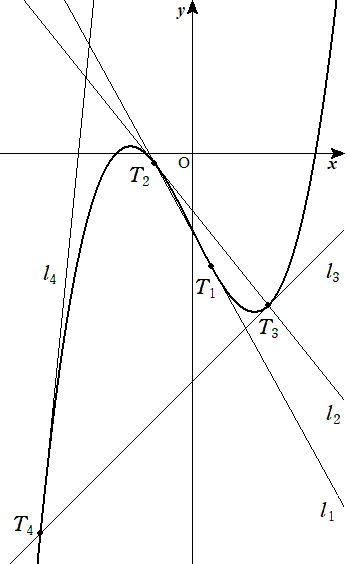



  18. 3次曲線y=f(x)=ax3+bx2+cx+d上の異なる3点P(p，f(p))，Q(q，f(q))，R(r，f(r))について，
    (1)　△PQRの面積を求めよ。
    (2)　P，Q，Rにおけるそれぞれの接線によって囲まれる三角形の面積Sを求めよ。


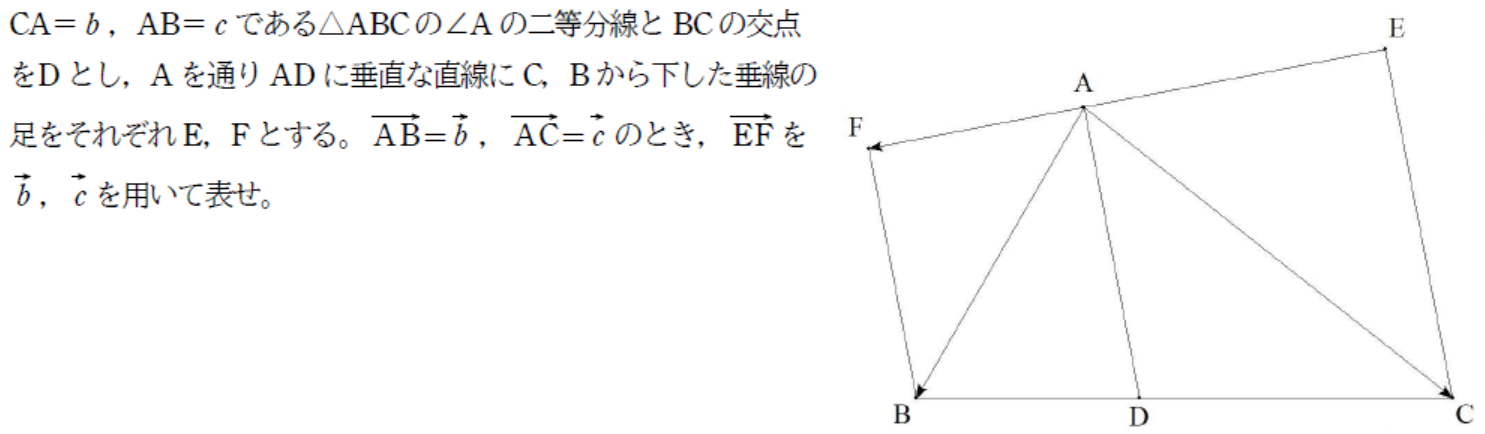
  19. △ABCの頂角の3等分線の辺に近い2つずつの等分線の交点を
    図のようにD，E，Fとする。
    B＝36°，C=54°，a＝8√2のとき，EFを求めよ。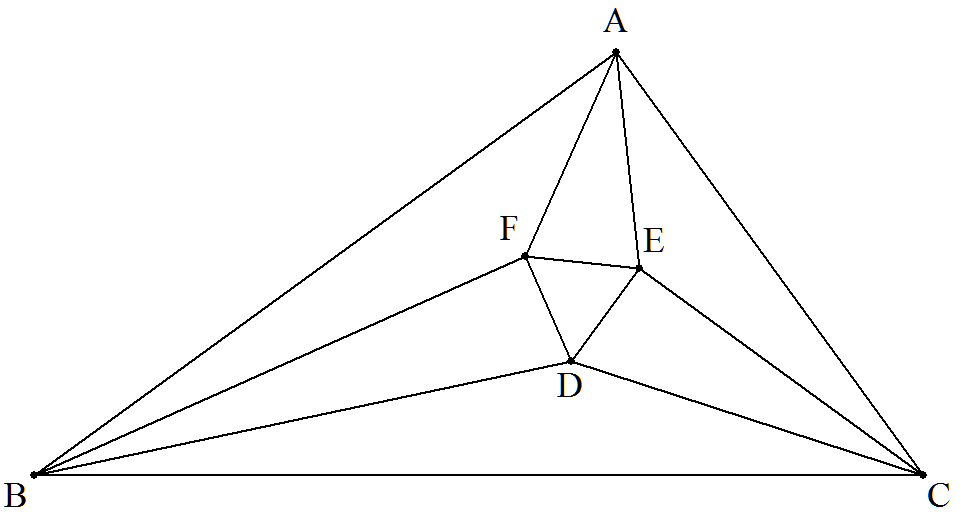



  20. 3点A(a,0,0)，B(0,b,0)，C(0,0,c)が定める平面αに原点Oから垂線OHを下ろす。
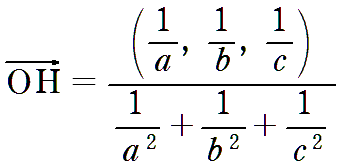    を示せ。



  21. BC=6，CA=5，AB=4である△ABCの内心を
    Iとし，AIとBC，BIとCA，CIとABの交点を
    それぞれD，E，Fとする。
    △AFE，△BDF，△CEDの内心をそれぞれ
    P，Q，Rとするとき，△PQRの面積を求めよ。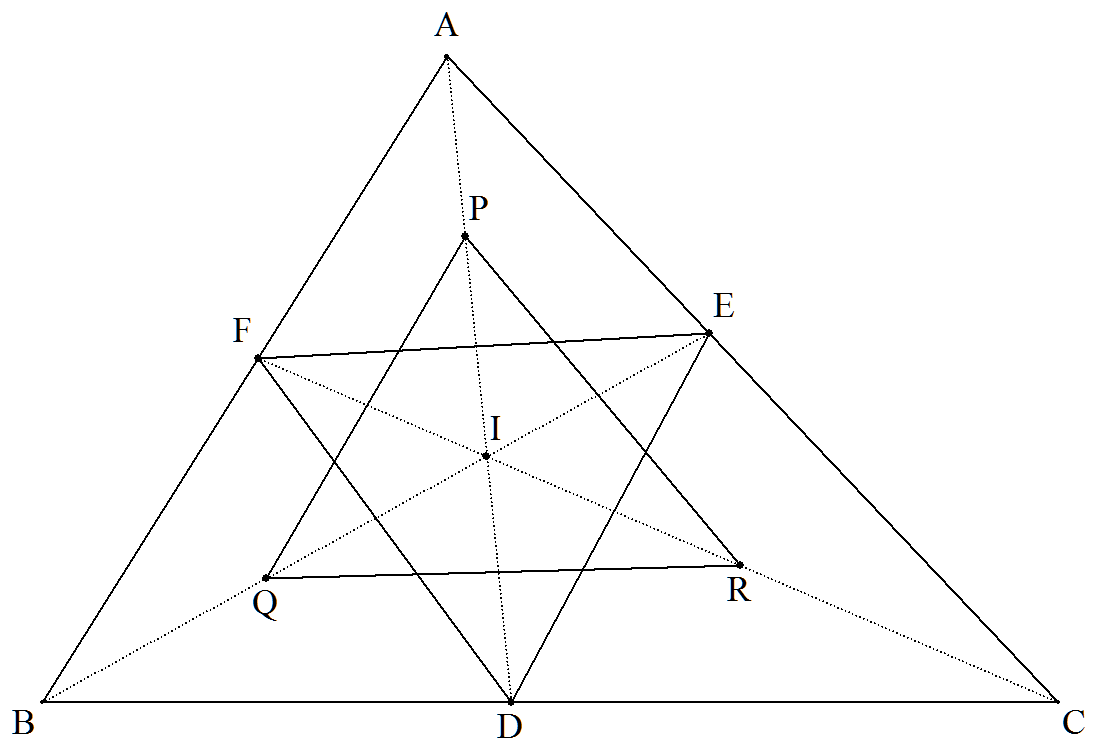



  22. 円に内接する四角形ABCDの外側に直角二等辺
    三角形PAD，QBA，RCB，SDCをつくる。
    四角形PQRS－四角形ABCDの値を求めよ。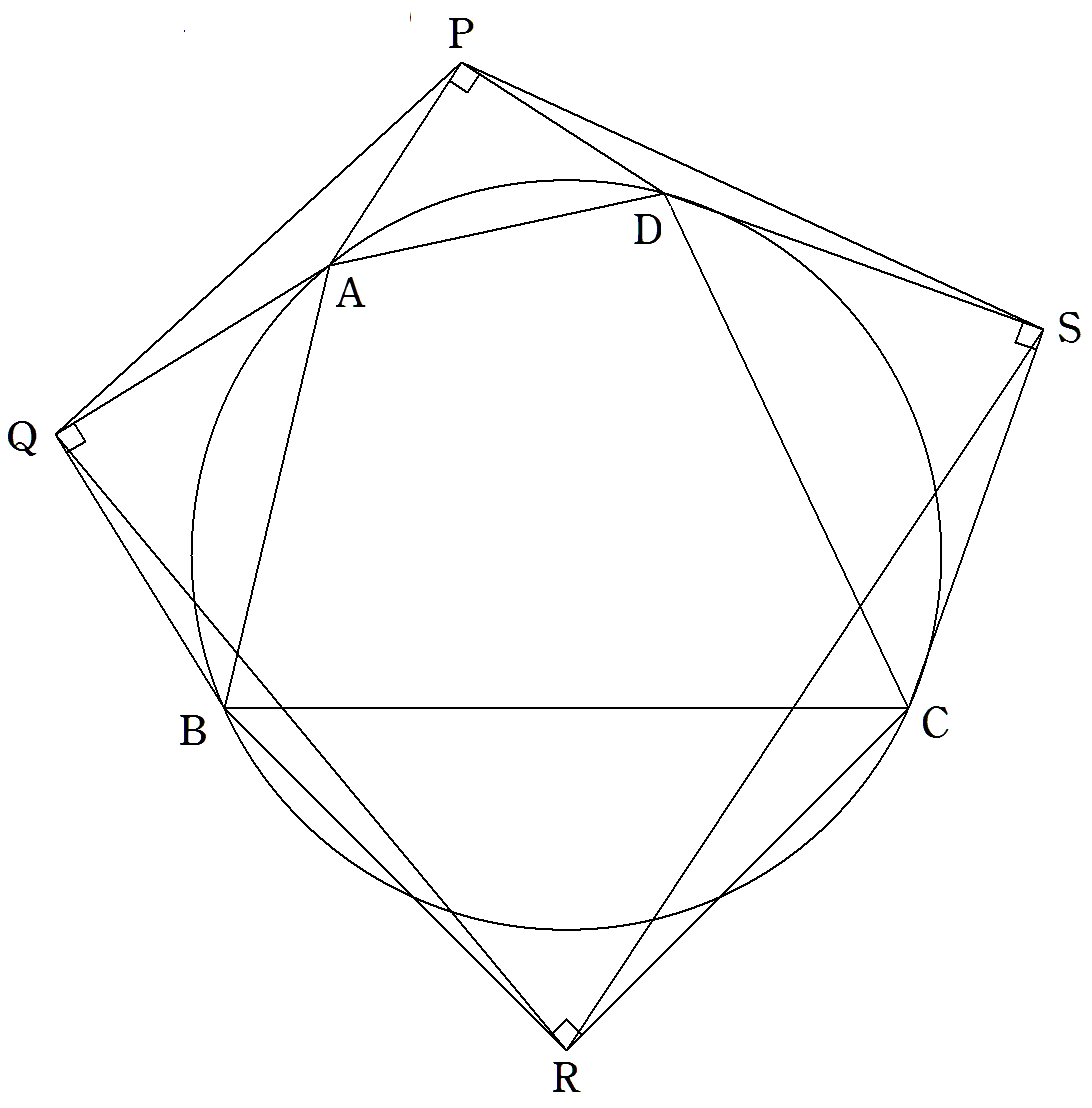



  23. (1)　nを2以上の整数とし，a1，a2，a3，…，anはすべて異なる実数とする。
    積の微分法を使わずに，f(x)=(x-a1)(x-a2)(x-a3)…(x-an)のx=a1における微分係数を求めよ。
    (2)　kは1から2020までの整数とする。
    f(x)=(x-1)(x-2)(x-3)…(x-2020)のx=kにおける微分係数が最大になるときのkの値と，
    その最大値を素因数分解したとき，5の因数の個数を求めよ。


  24. 0＜α＜π/4，0＜β＜π/4のとき，次の不等式を証明せよ。
    (tanα+tanβ)/2≧tan{(α+β)/2}≧√(tanαtanβ)


  25. 0＜α＜π/2，0＜β＜π/2のとき，次の3式の大小を不等式で表せ。
    (1)　(sinα+sinβ)/2，sin{(α+β)/2}，√(sinαsinβ)
    (2)　(cosα+cosβ)/2，cos{(α+β)/2}，√(cosαcosβ)


  26. 次の式を簡単にせよ。
    [tanα+tanβ-2tan{(α+β)/2}]/[tan2{(α+β)/2}-tanαtanβ]


  27. 次の式の値を求めよ。
    (tan215°-tan12°tan18°)/(tan12°+tan18°-2tan15°)


  28. ∠B＝63°，∠C＝72°，BC＝4√2である△ABCについて，
    (1)　頂角の三等分線の辺に近い2辺ずつの交点を図のよう
    　　にD，E，Fとするとき，EFを求めよ。
    (2)　頂角の外角の三等分線の辺に近い2辺ずつの交点を
    　　図のようにD´，E´，F´とするとき，E´F´を求めよ。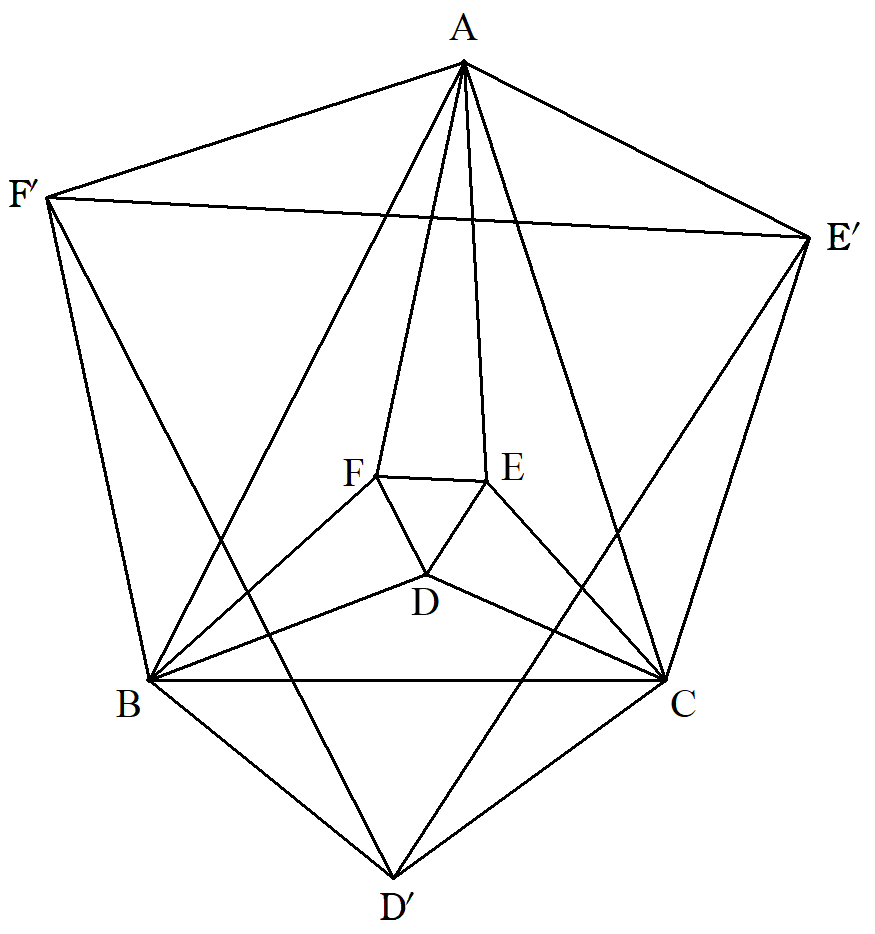



  29. 20を左右対称に，4以上の整数の和に分解すると，自分自身も含めて次の11通りある。
    {20，10+10，8+4+8，7+6+7，6+8+6，6+4+4+6，5+10+5，5+5+5+5，4+12+4，
    4+6+6+4，4+4+4+4+4}
    同様に，40を左右対称に，4以上の整数の和に分解すると，自分自身も含めて何通りあるか。


  30. △ABCの外心をO，内心をIとする。外接円とAI，BI，CIの延長との交点を
    それぞれD，E，Fとする。
    次の面積を，△ABCの面積S，外接円の半径R，内接円の半径rを用いて表せ。
    (1)　△DEF
    (2)　六角形AFBDCE
    (3)　△ABCと△DEFの重なる部分の六角形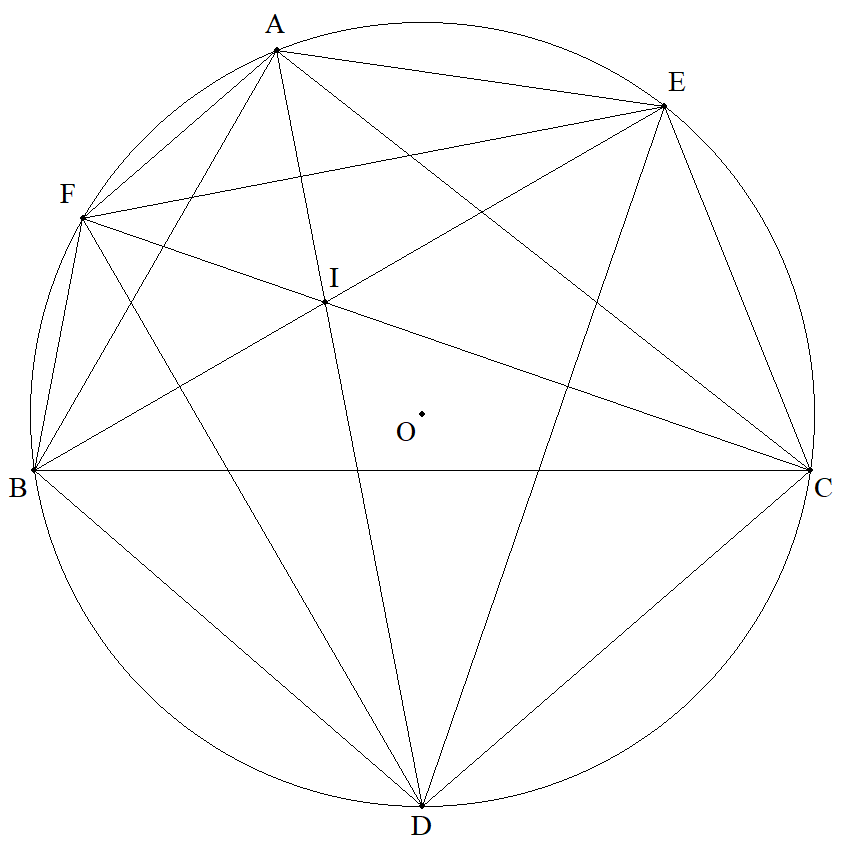



  31. ∠A＝90°，CA＝b，AB＝cである△ABCについて，
    Bを中心，半径cの円とBCとの交点をDとする。
    (1)　弧AD，AB，BCに接する円Pの半径r1を求めよ。
    (2)　弧AD，BC，CAに接する円Qの半径r2を求めよ。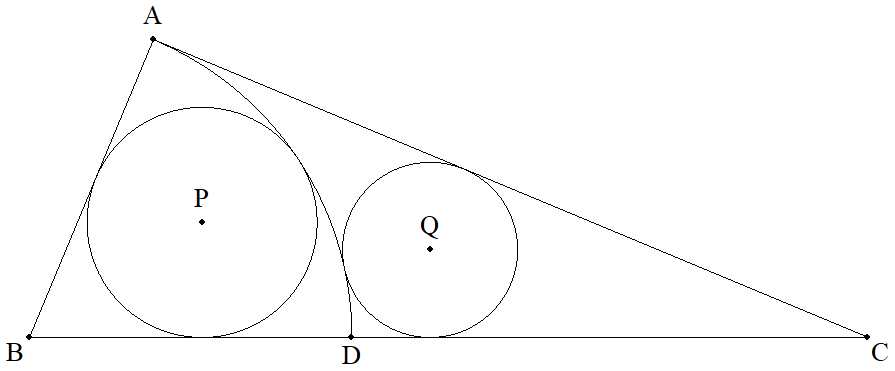



  32. f(n)を√nに最も近い整数とするとき，ΣK=1n(n+1) 1/f(k)の値を求めよ。


  33. f(n)を4乗根nに最も近い整数とするとき，
    (1)　ΣK=12023 1/f(k)の値を求めよ。
    (2)　ΣK=1N 1/f(k)＝6000となるNを求めよ。



  34. a＞0，b＞0，c＞0のとき，次の数列{an}の一般項を求めよ。
    a1=a，a2=b，an+2=can+1an


  35. n=10112のとき，Σk=1n(1/√k)の整数部分を求めよ。


  36. 1辺1の正九角形6個で囲まれる図形の面積Sを，
    sin20°＝aとして，aを用いて簡単な式で表せ。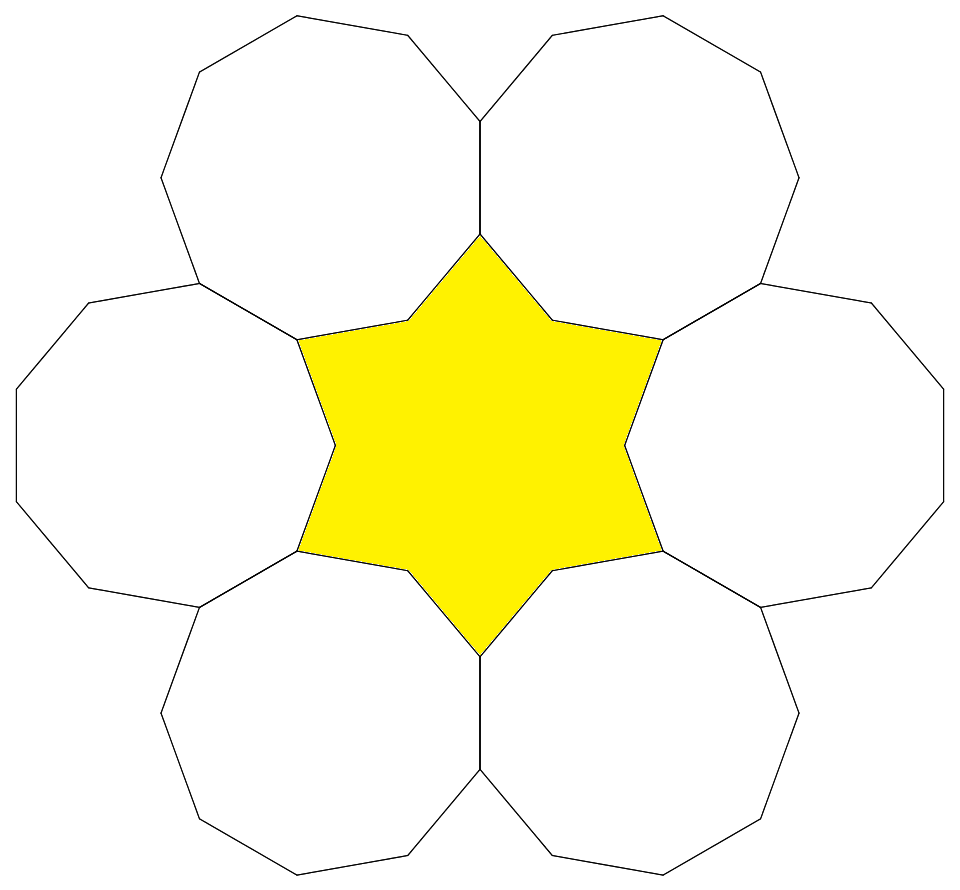


  37. 1辺が1である正七角形①，②，…，⑩が，
    図のように配置されている。
    それらによって囲まれる18角形の面積を
    Sとする。
    π/7＝θとおき，Sをsinθ，sin2θ，sin3θ
    を用いて表せ。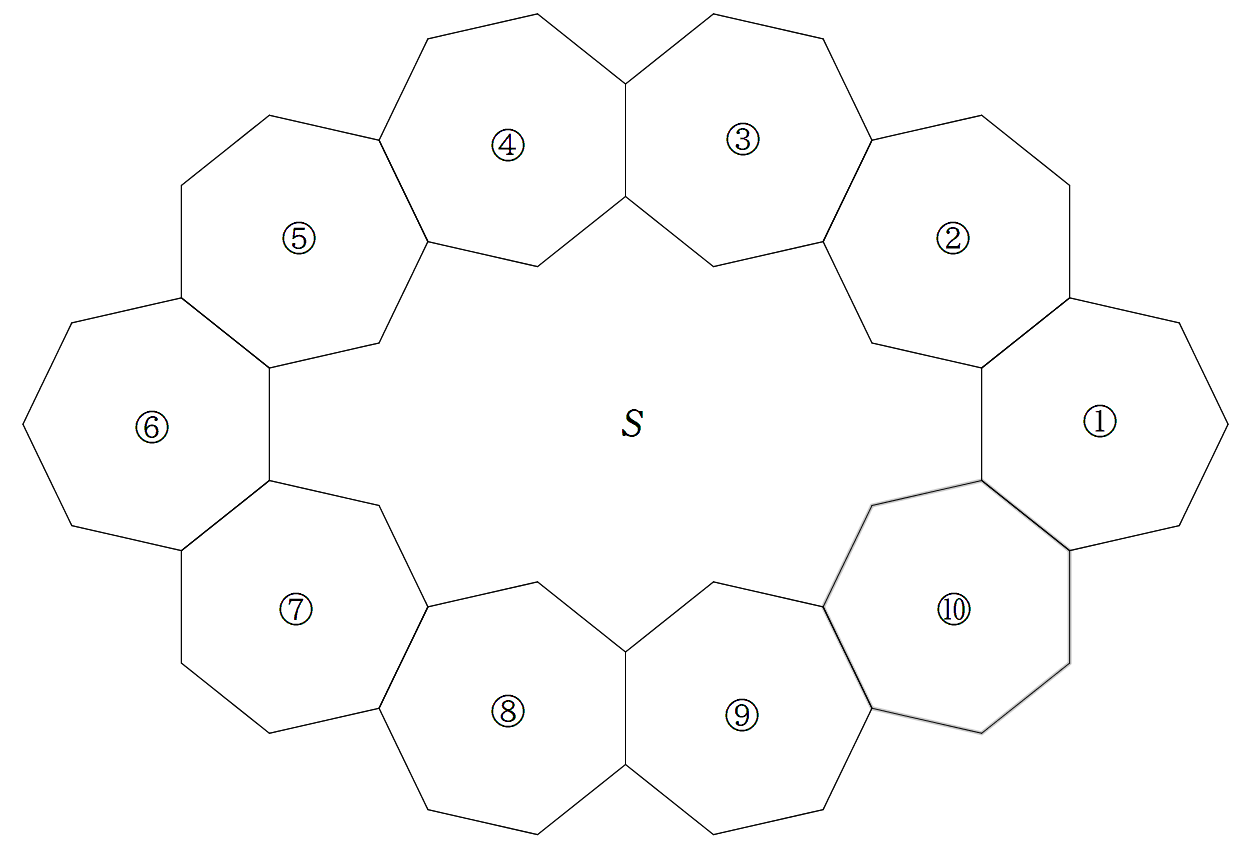


  38. 図のように，鋭角三角形ABCの傍接円I1，I2，I3の2円ずつの
    共通外接線で囲まれる△A′B′C′について，次を証明せよ。
    △A′B′C′/△ABC＝(1+cosA+cosB+cosC)2/2cosAcosBcosC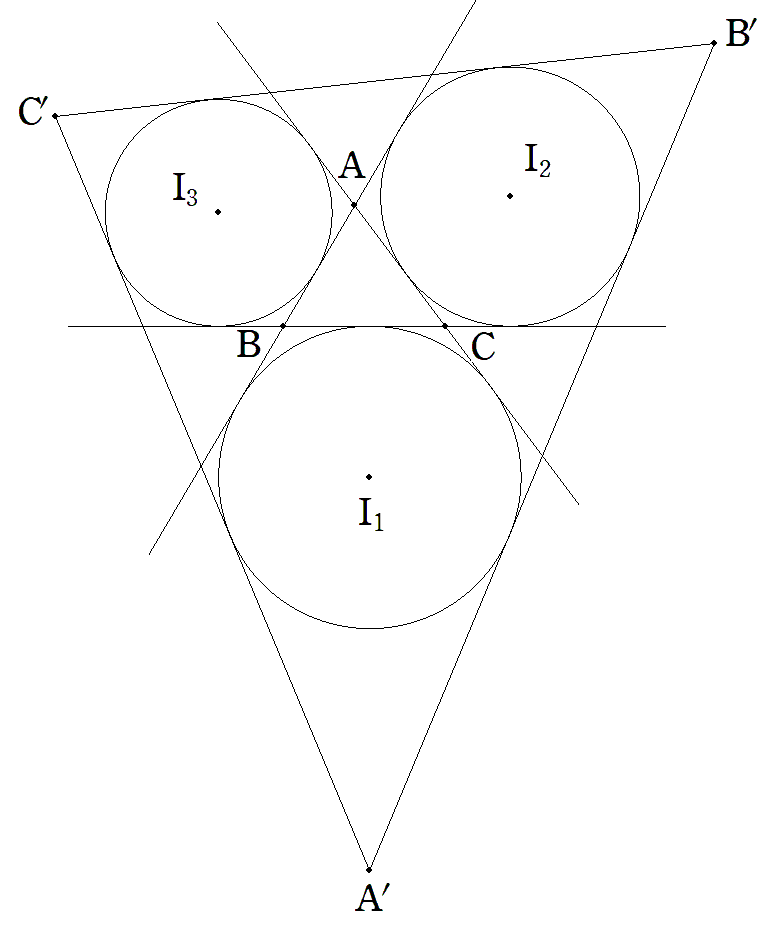


  39. 四角形ABCDにおいて，AB＝4， BC＝CD＝DA，∠B＝90°である。
    (1)　∠A＝60°のとき，BCを求めよ。
    (2)　BC＝3のとき，BDを求めよ．





  41. 　





  43. 四角形ABCDは円に外接し，図のように接点をE，F，
    G，Hとし，AE=a，BF＝b，CG=c，DH＝dとする。
    図のように，四角形の辺あるいはその延長に接する
    4つの円の中心をそれぞれP，Q，R，Sとするとき，
    (四角形PQRS)/(四角形ABCD)の値を求めよ。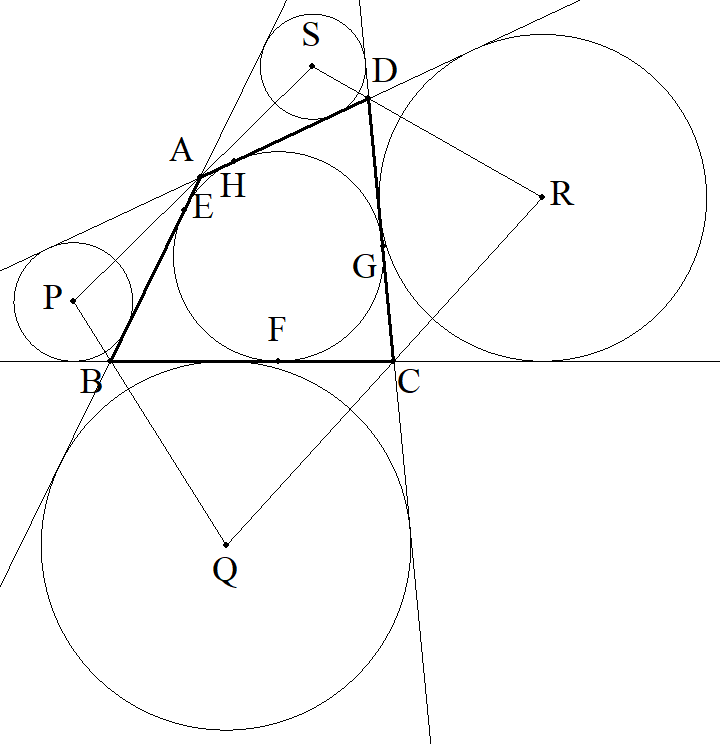


  44. 半径1の甲円に図のように乙円5個と
    丙円1個が配置されている。
    丙円の半径を求めよ。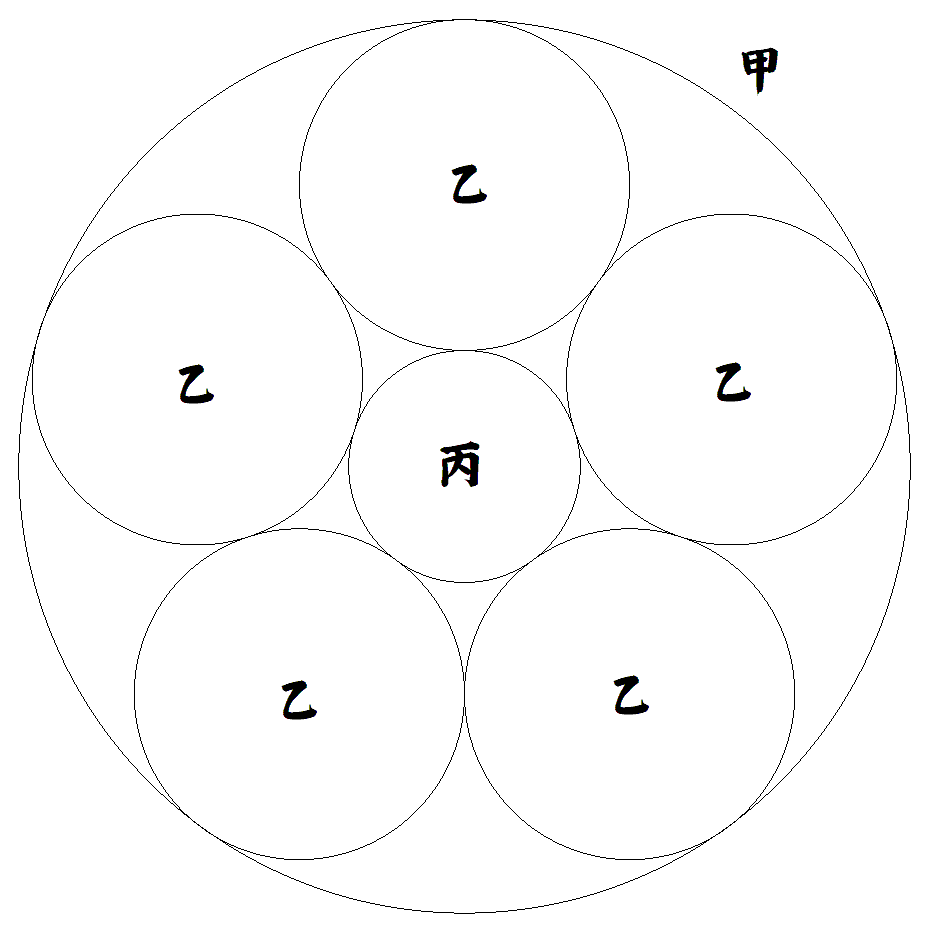


  45. ∠A＝Aである△ABCの内接円とBCとの接点をDとする。
    BD＝p，DC＝qのとき，△ABCの面積を，A，p，qを
    用いて表せ。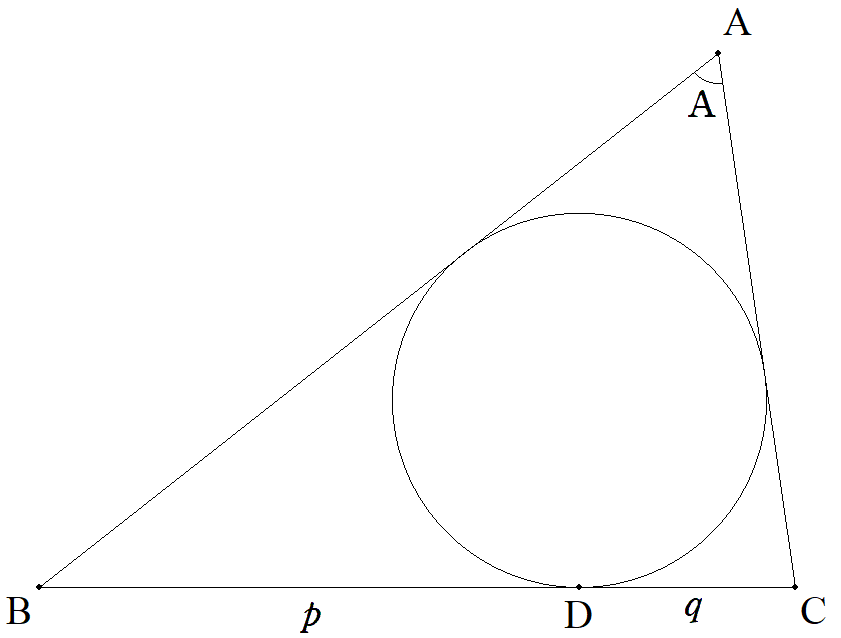





  47. 四角形ABCDについて，cosA+cosB+cosC+cosD=0のとき，四角形の形状を求めよ。


  48. 平行四辺形ABCDの外側に正方形AEFB，
    BGHC，CJKD，DLMAをつくる。
    正方形の対角線の交点を図のようにそれ
    ぞれP，Q，R，Sとする。
    次を証明せよ。
    (1)　四角形PQRSは正方形となる。
    (2)　四角形PQRSの対角線の交点と平行
    　　四辺形ABCDの交点は一致する。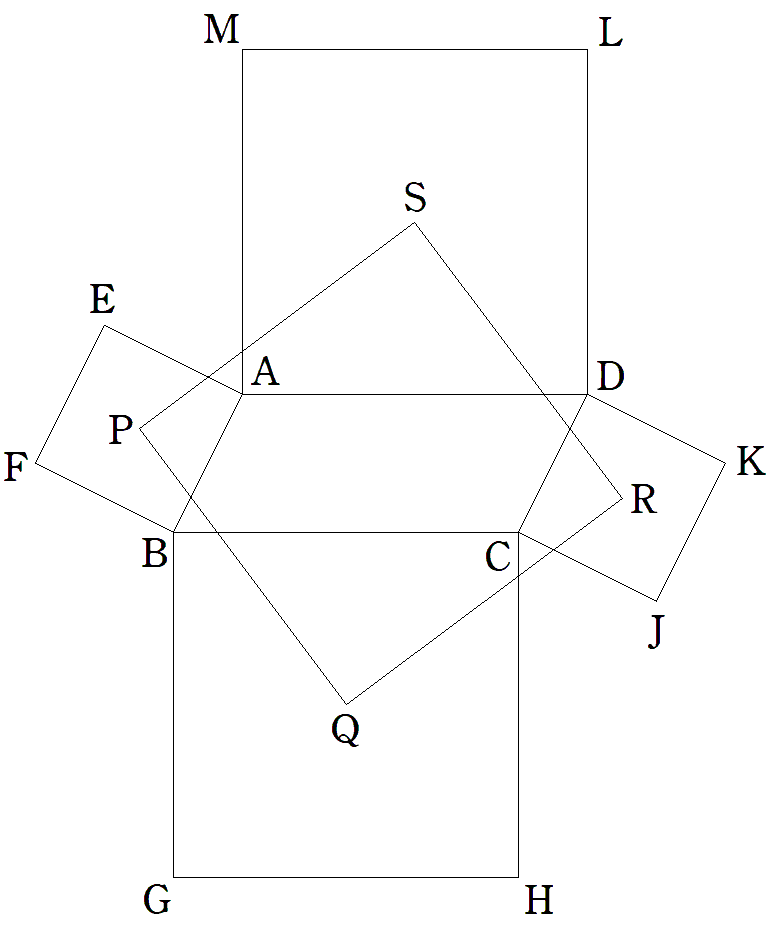




  49. a，b，cは△ABCの3辺で，acosθｰbcosθ=c，2abcos2θ+(a2-b2)sin2θ=kc2を満たしている。
    θとkがどのように変化しても，∠Cは鈍角になることはないことを証明せよ。


  50. 次を証明せよ。
    (1)　sin5θ＝16sin5θ-20sin3θ+5sinθ
    　　cos5θ＝16cos5θ-20cos3θ+5cosθ
    (2)　tanθ+tan(π/5＋θ)+tan(2π/5＋θ)+tan(3π/5＋θ)+tan(4π/5＋θ)=5tan5θ