|
2つの放物線y=x2+a,x=y2+aの3本の共通接線が 正三角形をつくるとき,その面積を求めよ。 | 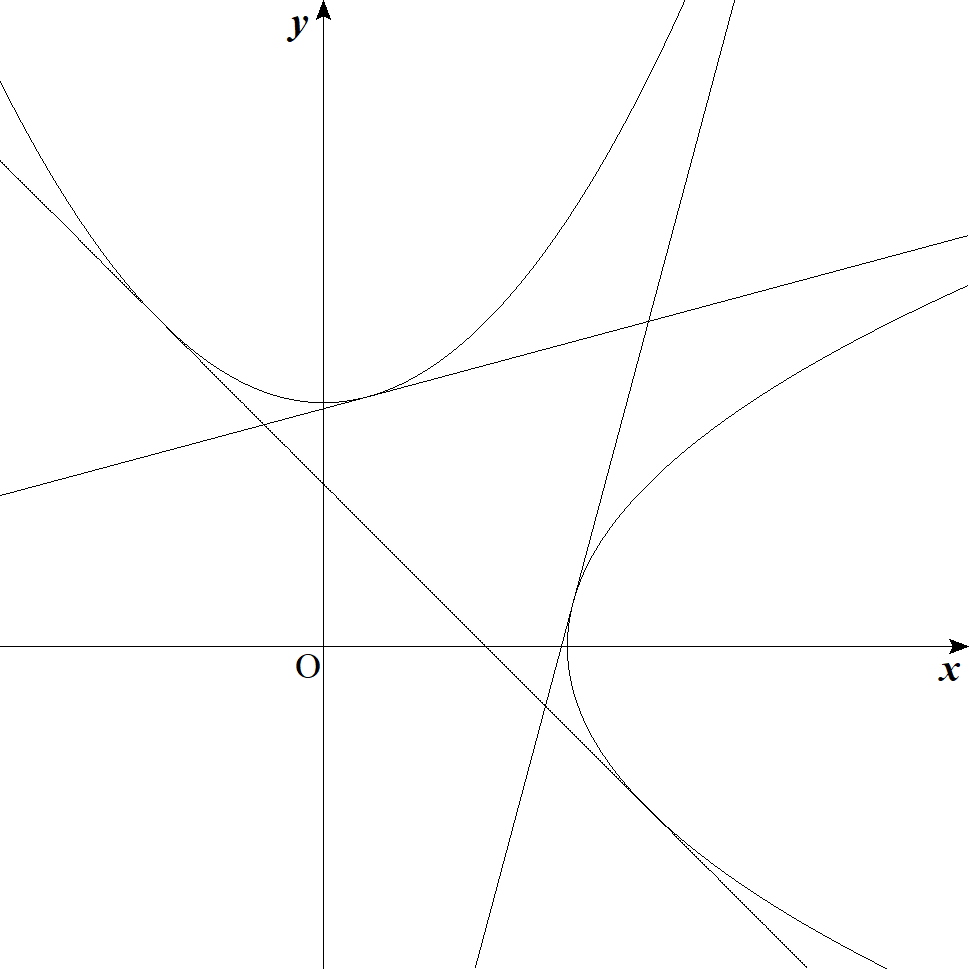 |
|
四角形ABCDについて,AD∥BC,∠ABD=30°-2θ,∠DBC=3θ, ∠BDC=60°-θ,BC=aのとき,四角形の面積を求めよ。 ただし,0°<θ<15°とする。 | 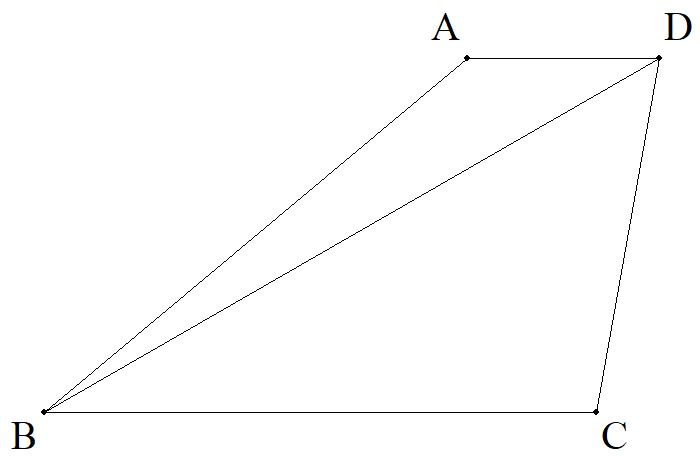 |
数列1,2,2,3,3,3,4,4,4,4,5,…について,
(1) 第2020項を求めよ。
(2) 初項から第2020項までの和を求めよ。
(3) 初項から第n項までの和が,2020以上となる最小のnの値を求めよ。
(4) 初項から第2020項までの和より,第2021項から第n項までの和の方が大きくなる最小のnの値を求めよ。
|
右図のように,自然数1を中心にして,その周りに数を配置していく。 (1) 全ての数の和を,nを用いて表せ。 (2) (1)の和が2021の倍数となる最小のnの値を求めよ。 | 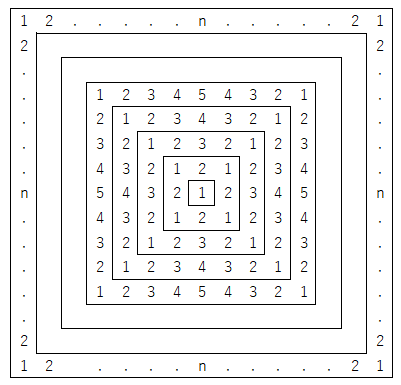 |
0<A<B<C<π/4を満たす角A,B,Cは等差数列をなし,(1+tanA)/(1+tanB)=(1+tanB)/(1+tanC)のとき,
tanBの値を求めよ。

|  |
|
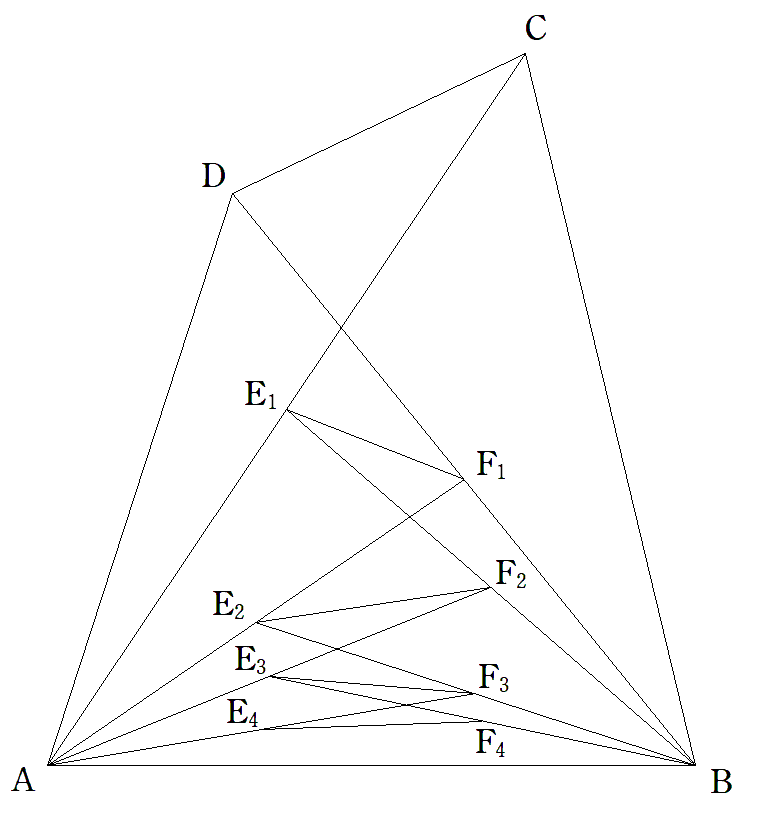
△ABCのBCの中点をD,CA上にE,AB上にFを, △DEFが正三角形になるようにとる。 次の場合に,正三角形の1辺を求めよ。 (1) AE=7,EC=5,AF=6,FB=8 (2) AE=2,EC=4,AF=3 (3) BC=5,CA=7,AB=8 | 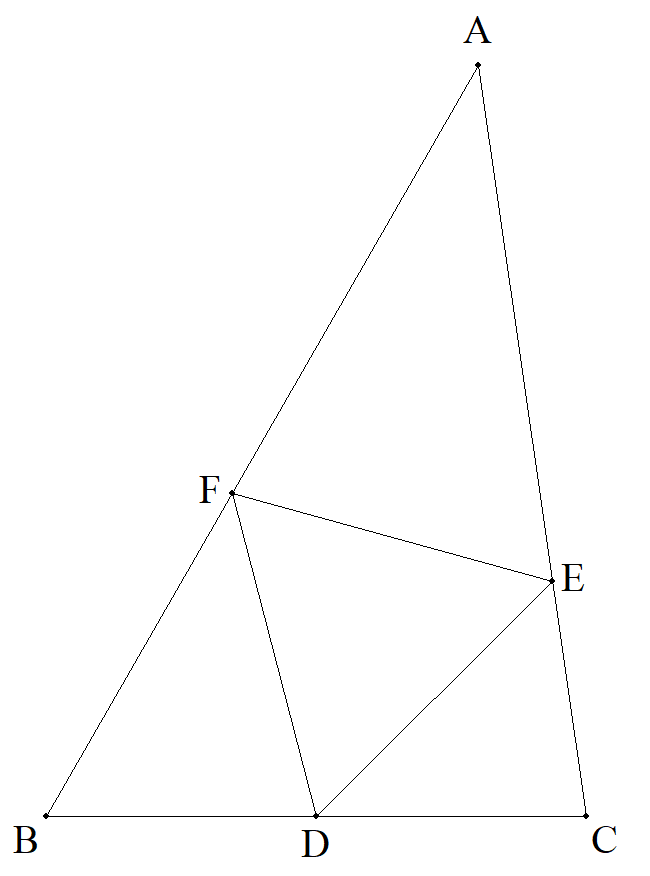 |
|
平行四辺形ABCDについて, ADをs:(1-s)に内分する点をP, BPをs:(1-s)に内分する点をQ, CQをs:(1-s)に内分する点をR, DRをs:(1-s)に内分する点をS, △QRSの重心をGとする。(0<s<1) (1) GがAC上にあるとき,sの満たす 最低次の方程式を1つ求めよ。 (2) GがBD上にあるとき,sの満たす 最低次の方程式を1つ求めよ。 | 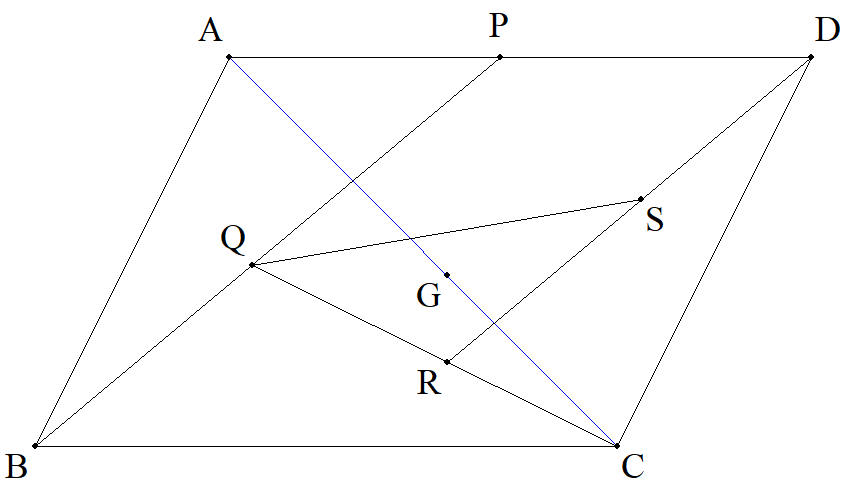 |
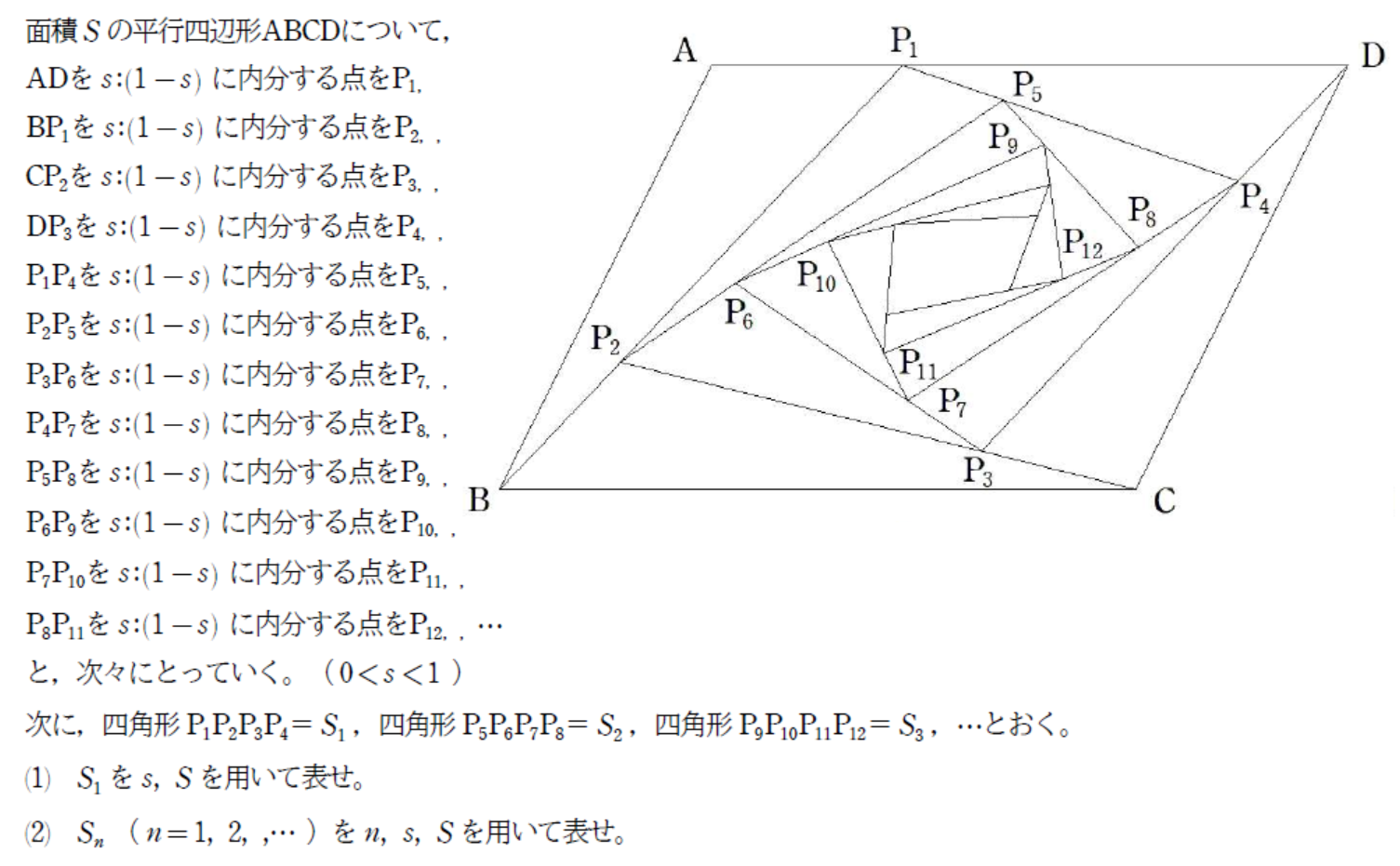
|
面積Sの平行四辺形ABCDについて, ADをs:(1-s)に内分する点をE, ABをt:(1-t)に内分する点をF, BEとDFの交点をG, BEとCFの交点をH, CEとDFの交点をIとする。 △GHIの面積をs,t,Sを用いて表せ。 ただし,0<s<1,0<t<1とする。 | 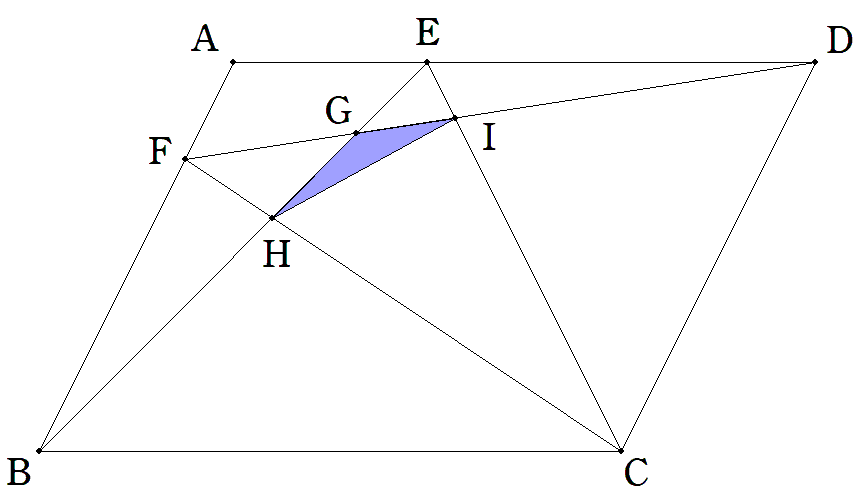 |
|
△ABCのAB,CAを1辺とする正方形ADEB,ACFGを 三角形の外側につくり,さらに,BF,CEを1辺とする 正方形BHIF,CEJKをAを含まない方につくる。 (1) H,Kは一致することを証明せよ。 (2) △BHC=a2/2+△ABCを証明せよ。 (3) 正方形BHIFとCEJKの面積の和がEFを一辺とする 正方形の面積に等しくなるとき,△ABCの3辺 a,b,cの関係式を求めよ。 | 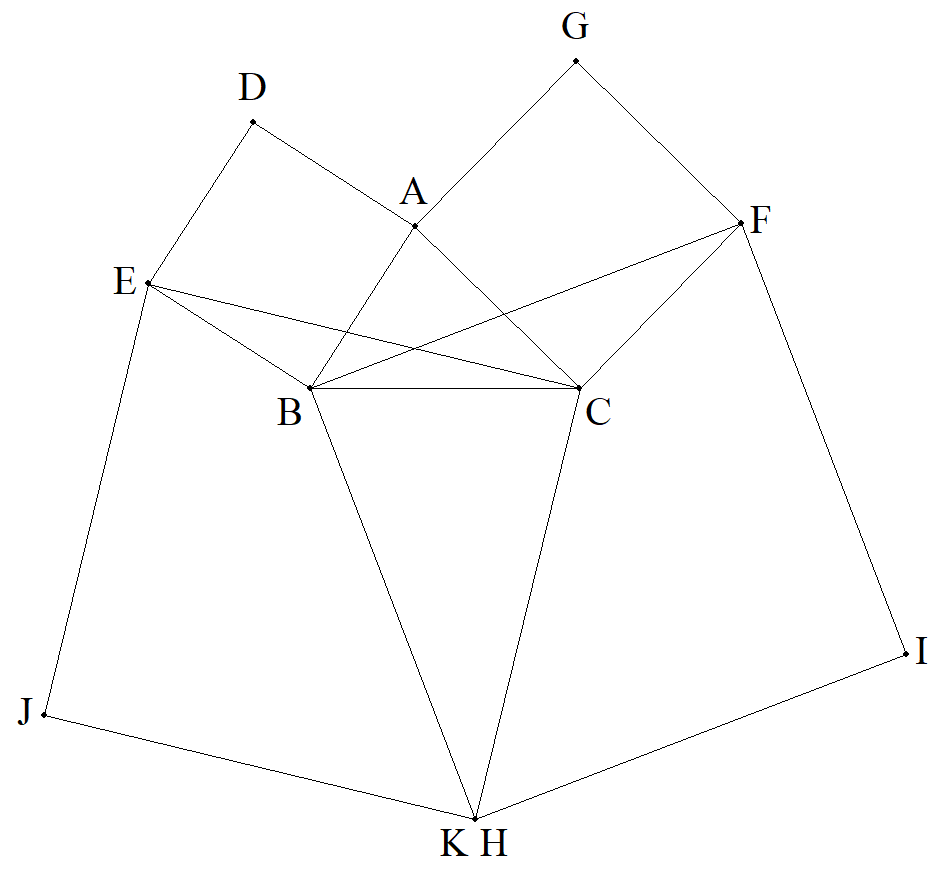 |
|
∠A=∠B=∠E=90°である五角形ABCDEについて, BCを直径とする円に外接し,辺AB,CDに接する 円の中心をP,DEを直径とする円に外接し,辺CD, EAに接する円の中心をQとする。 このとき,CP⊥DQを証明せよ。 | 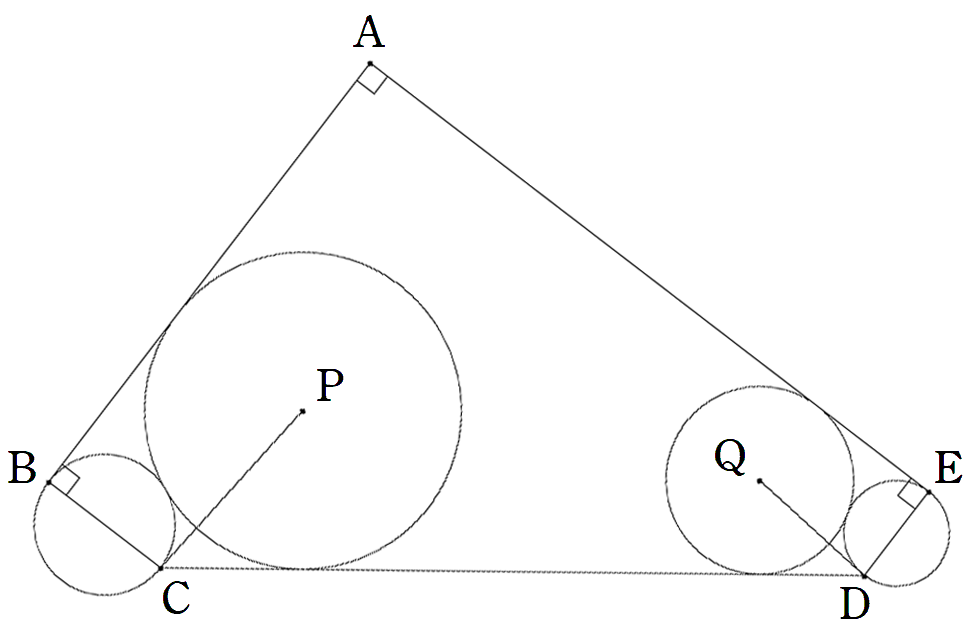 |
|
3点A(5,12),B(0,0),C(14,0)について,点Aを通り, BC上の点Dに接する円の中心をPとする。 (1) 点DがBC上を動くとき,点Pの軌跡の方程式を求めよ。 (2) 点Pの軌跡と,AB,ACで囲まれる図形の面積を求めよ。 | 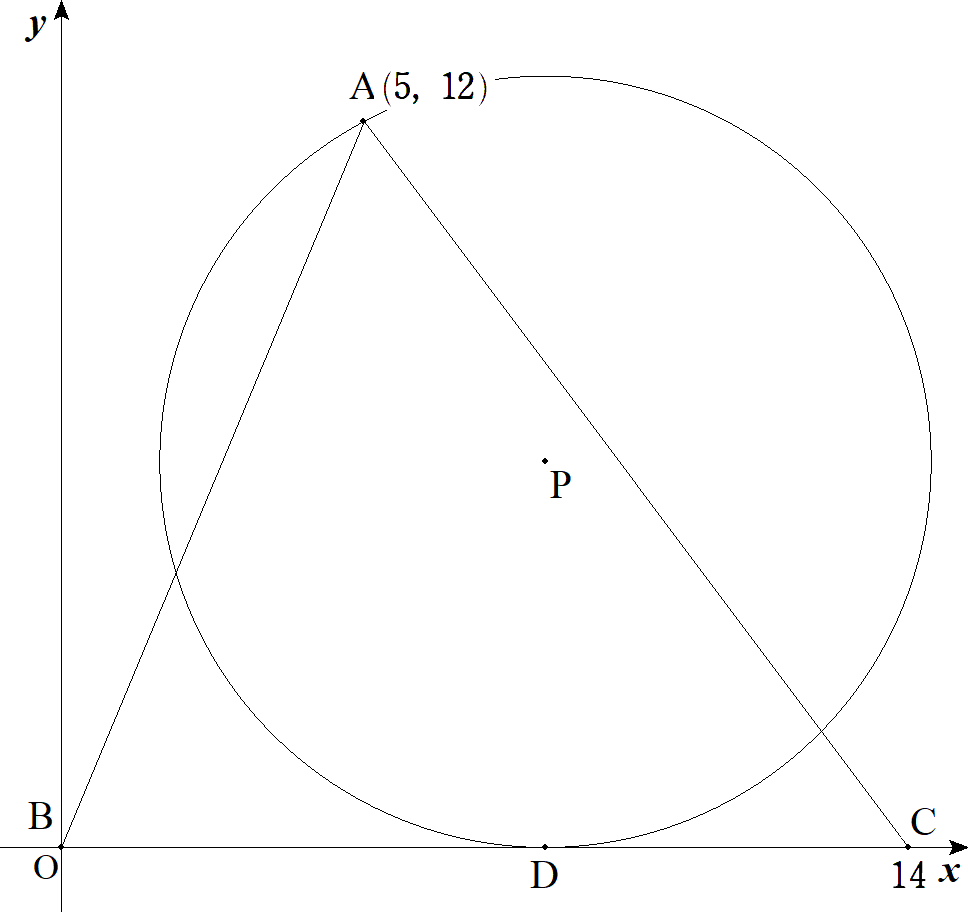 |
|
2個の同じ楕円の長軸は同一直線上にあり,長軸の 端で外接している。図のように,小円は楕円に内接 し,その接点で大円と外接している。 楕円の長軸2a,短軸2b,小円の半径をrとするとき, 大円の半径Rを求めよ。 | 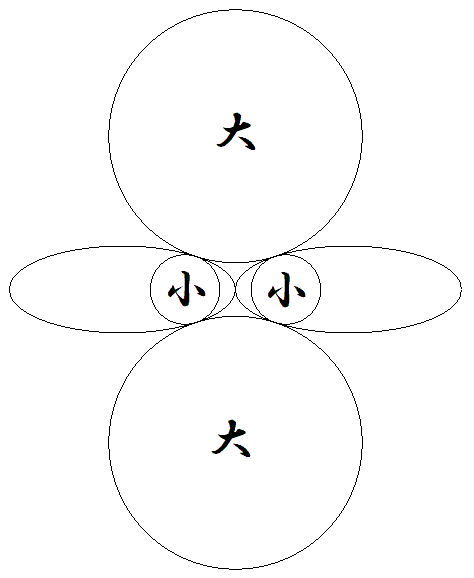 |
|
長方形内に2個の等しい楕円が図のように配置 されている。 楕円の長軸は長方形の縦に等しく平行である。 1個の楕円に2個の甲円が図のように内接し, 甲円同士は外接している。 乙円は,楕円と甲円の接点で甲円に外接し, 長方形にも接している。 このとき,長方形の縦横の比を求めよ。 | 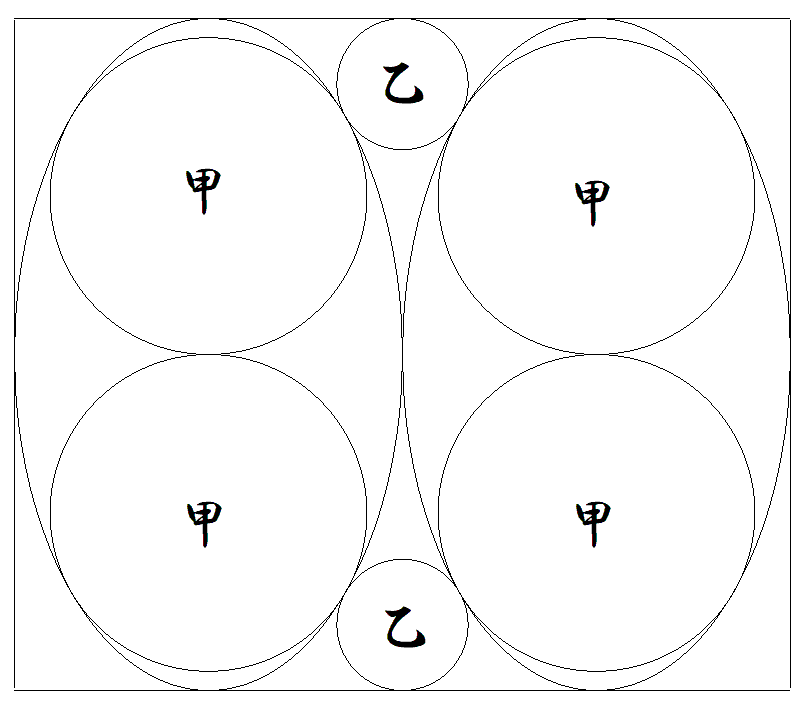 |
|
AB=a,BC=b,CD=c,DA=dである四角形ABCDは, 円に内接し,円に外接する。対角線AC,BDの交点をEとし, △EAB,△EBC,△ECD,△EDAの内接円の半径をそれぞれ r1,r2,r3,r4とするとき,r1:r2:r3:r4を求めよ。 | 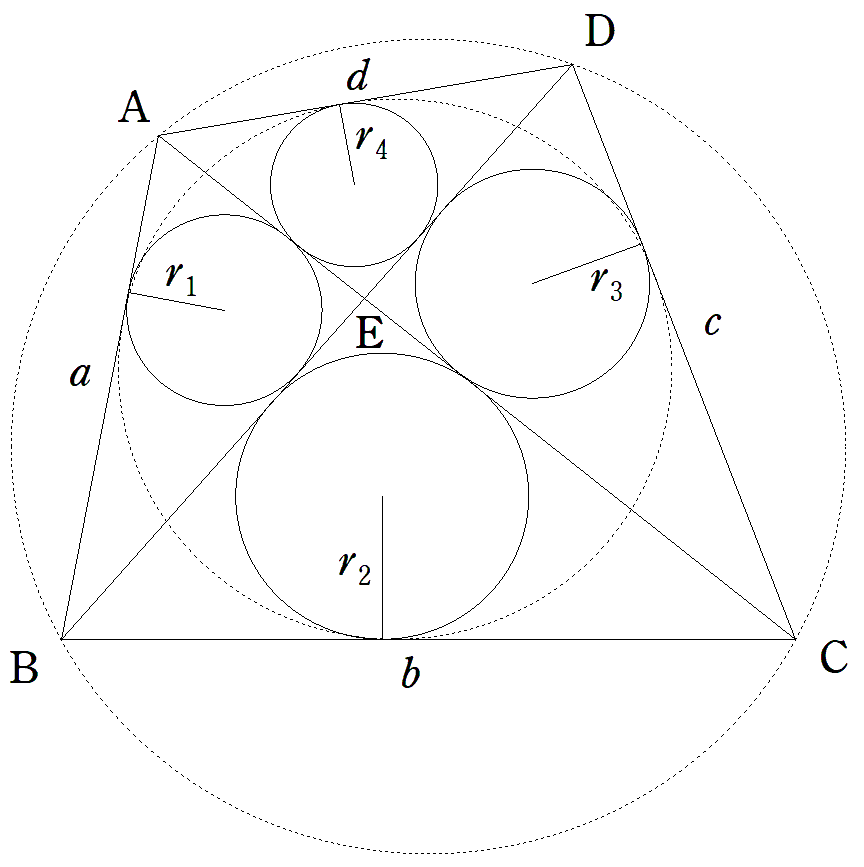 |
(1) 平面α:x+2y+3z+4=0に関して,点P(5,6,7)と対称な点Qの座標を求めよ。
(2) 平面α:ax+by+cz+d=0に関して,点P(x1,y1,z1)と対称な点をQ(x2,y2,z2)とする。
x2,y2,z2を求めよ。
(3) (2)で,点Pと平面αの距離hを求めよ。
|
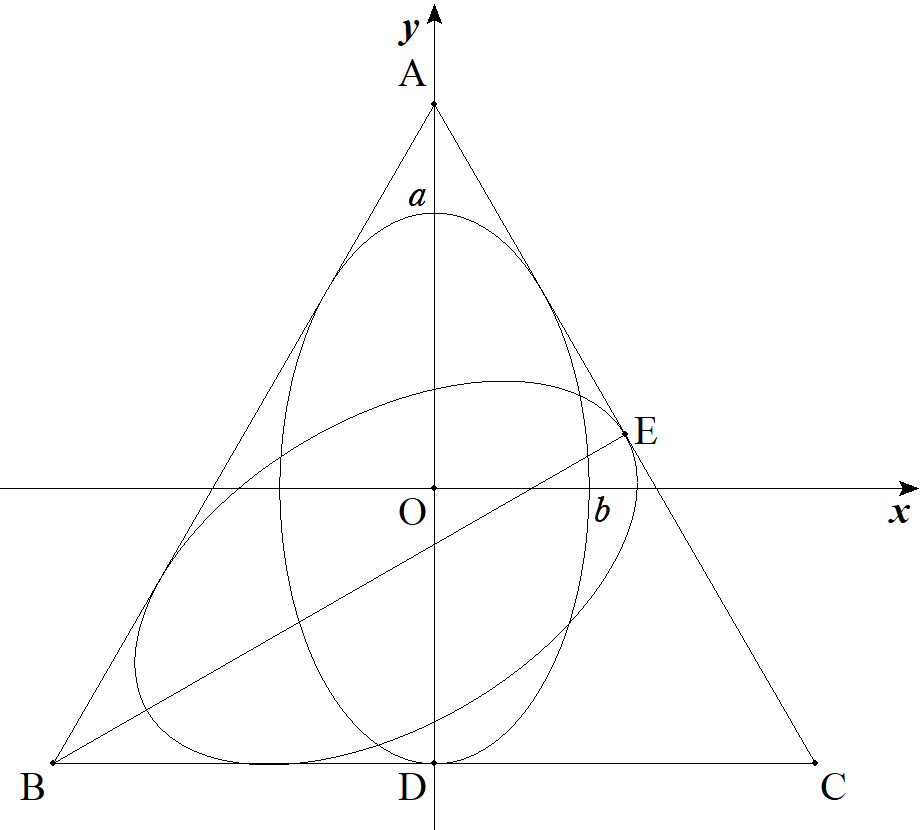
正三角形内に長軸2a,短軸2bの楕円を3個配置する。 ただし,楕円の長軸は正三角形の中線上にある。 このとき,正三角形の1辺を求めよ。 | 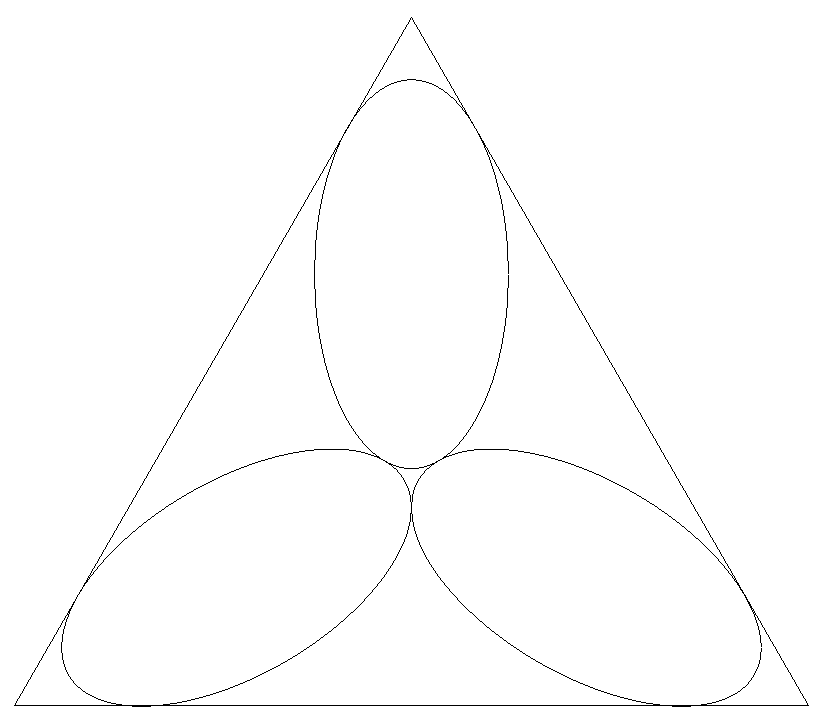 |
|
R>rとする。
半径R,rの同心円の間に,図のように n個の合同な楕円が連結して配置されている。 rをRを用いて表せ。 | 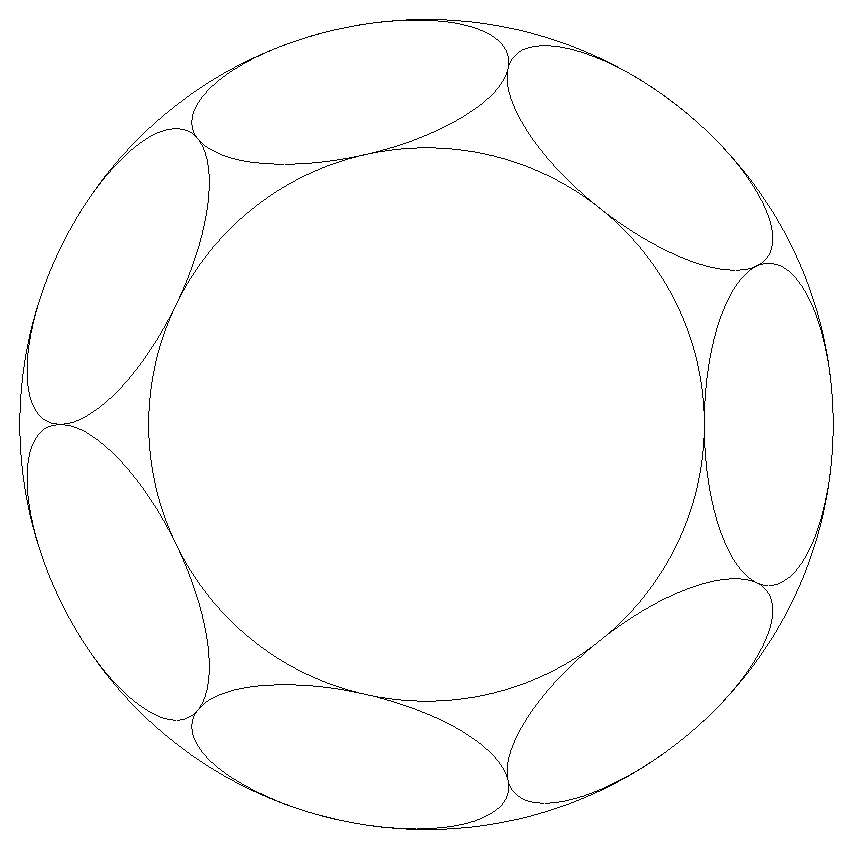 |
|
正n角形内に長軸2a,短軸2bの楕円n個を図のように配置する。 ただし,楕円の長軸は正n角形の頂点と中心を結んだ線分上にある。 このとき,正n角形の1辺を求めよ。 | 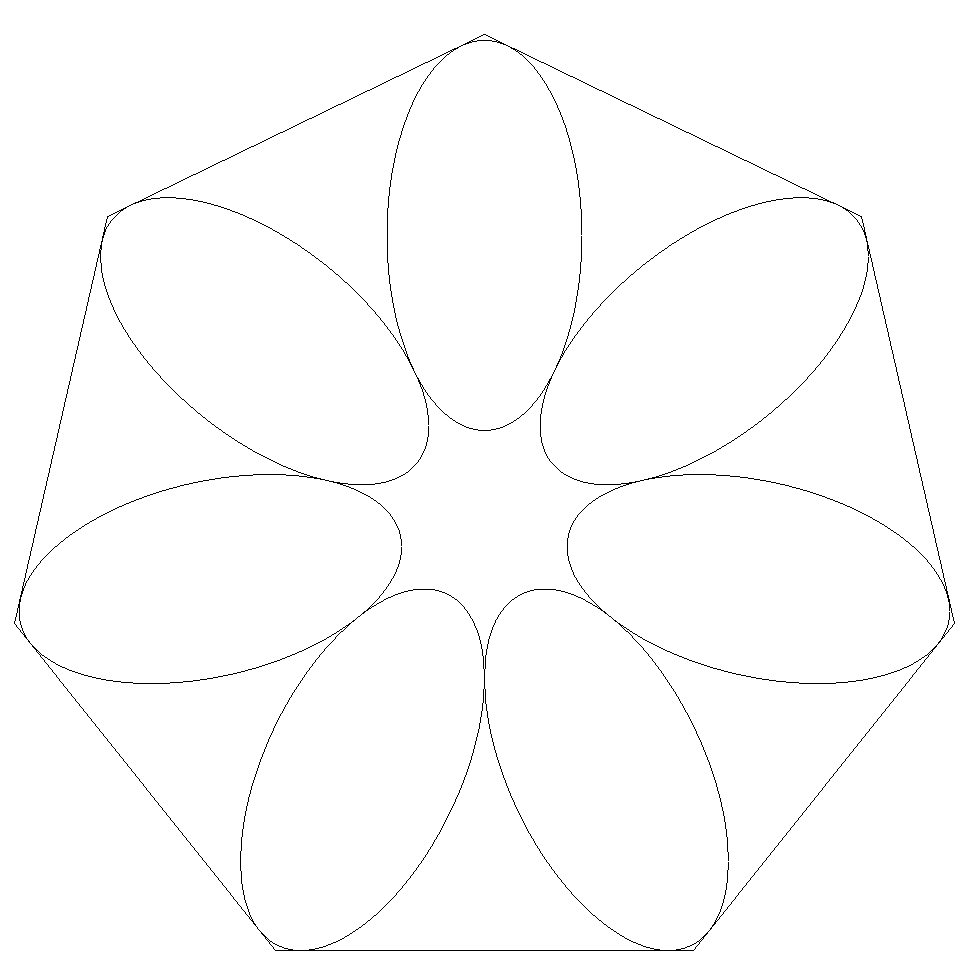 |
|
図のように,正三角形に合同な2個の楕円が配置されている。 縦長の楕円は,長軸が正三角形の中線に一致する。横長の 楕円は,正三角形の3辺に接し,短軸は中線上にある。 このとき,楕円の長軸÷短軸の値を求めよ。 | 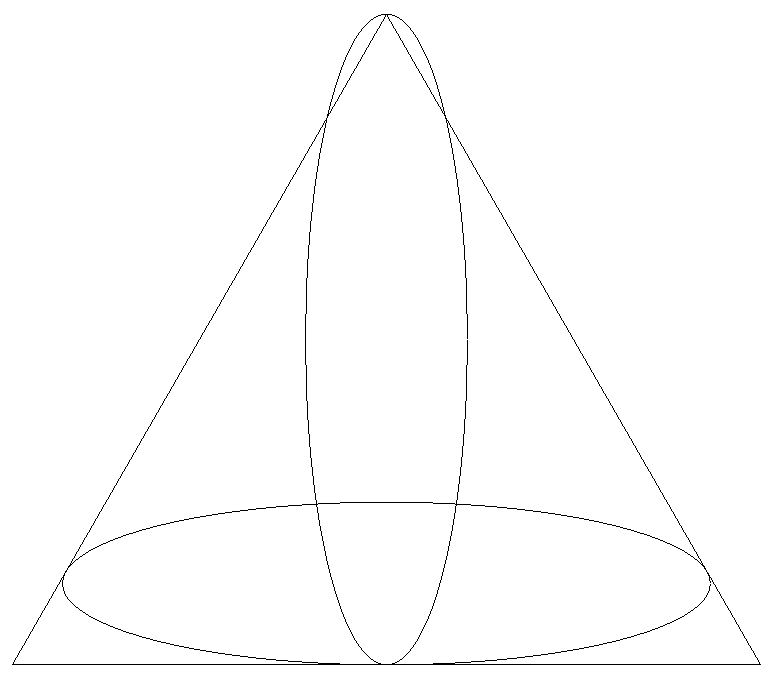 |
|
図のように,正三角形に楕円が内接し, 長軸は三角形の底辺に平行になるように 配置されている。 その楕円に外接し,正三角形の2辺に 接する円を考える。 楕円と円の面積が等しくなるとき, 楕円の長軸÷短軸の値を求めよ。 | 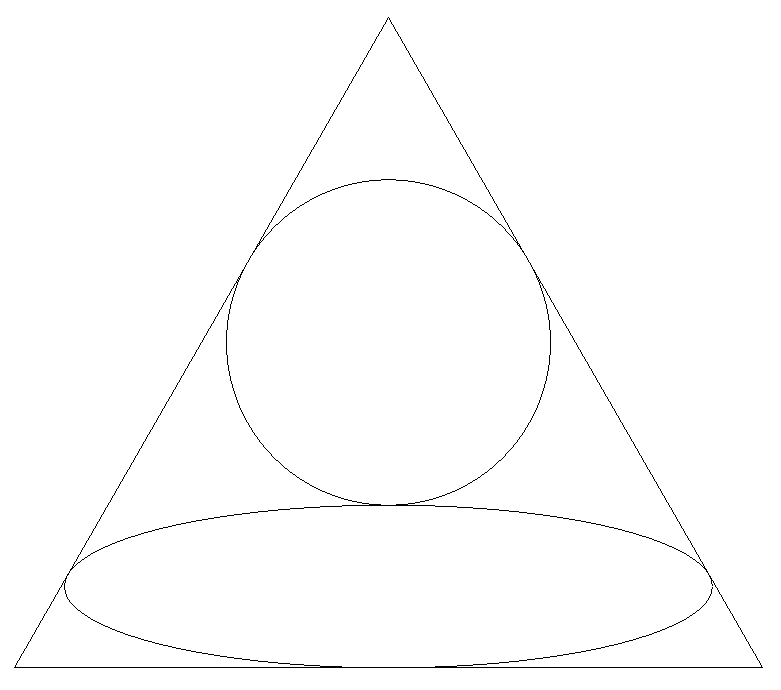 |
|
正方形内に楕円と2個の円が図のように配置されている。 楕円の長軸は正方形の対角線上にある。 円と楕円の面積が等しいとき,楕円の長軸÷短軸の値を求めよ。 | 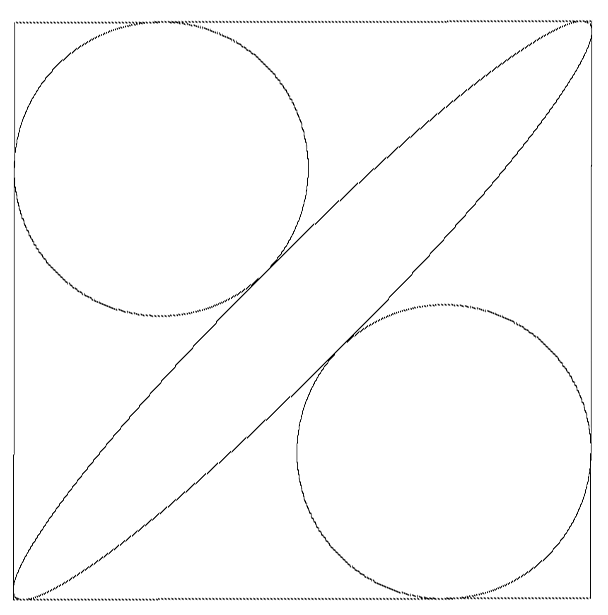 |
|
正方形内に楕円と4個の甲円が図のように配置されている。 楕円の長軸は正方形の対角線上にある。 楕円に内接する2円は,楕円の長軸の端で楕円に接している。 楕円に外接する2円は,正方形の2辺に接している。 このとき,楕円の長軸÷短軸の値を求めよ。 | 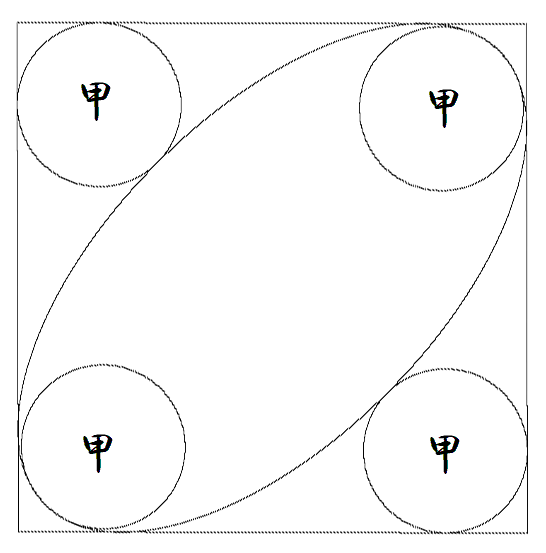 |
|
正三角形内に楕円と3個の甲円が図のように配置されている。 楕円の長軸は正三角形の底辺に平行である。 楕円に内接する2円は,楕円の長軸の端で楕円に接している。 楕円に外接する円は,正三角形の2辺に接している。 このとき,楕円の長軸÷短軸の値を求めよ。 | 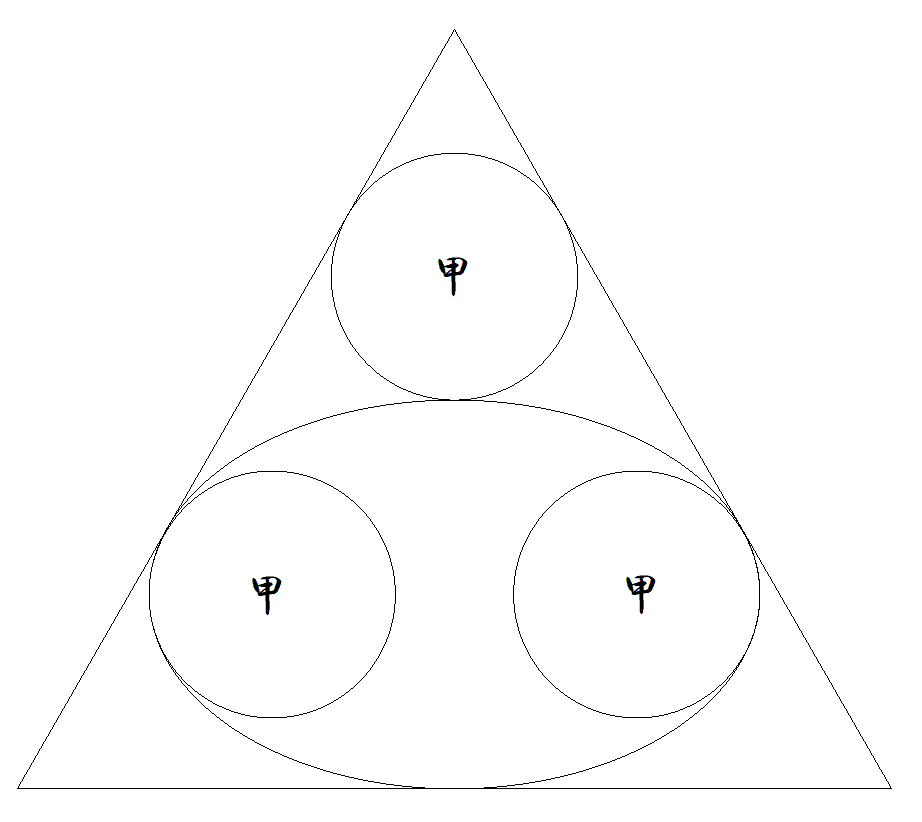 |
4次方程式x4+lx2+mx+n=0が重解をもつ条件を求めよ。
|
正三角形に長軸8,短軸2の楕円が内接している。 ただし,楕円の長軸は正三角形の底辺に平行である。 その楕円に外接し,正三角形の2辺に接する甲乙円 を図のように配置する。 (1) 甲円の半径を求めよ。 (2) 乙円の半径を求めよ。 | 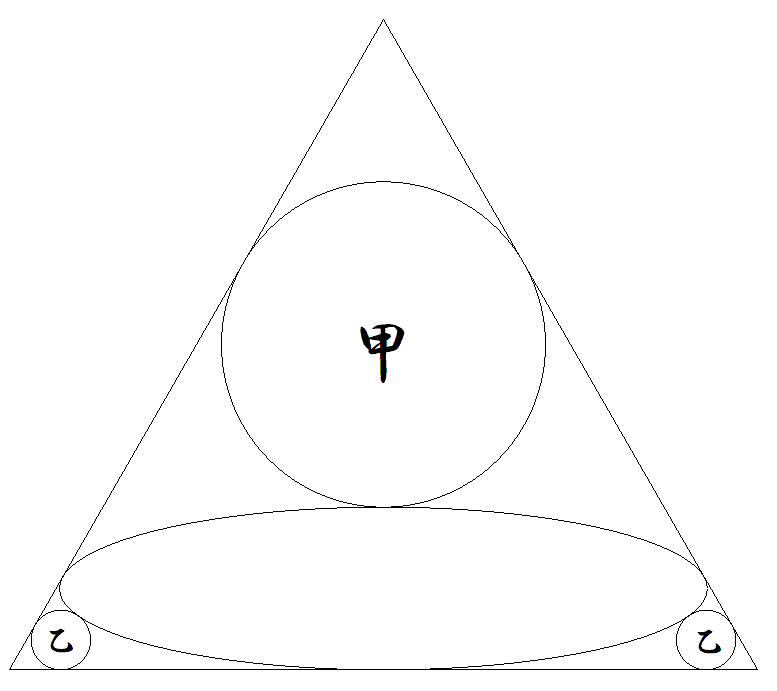 |
|
正三角形内に相似である甲,乙楕円が3個ずつ 図のように配置されている。 甲の長軸と乙の短軸は三角形の中線上にあり, 甲の短軸と乙の長軸が等しいとき, 長軸÷短軸の値を求めよ。 | 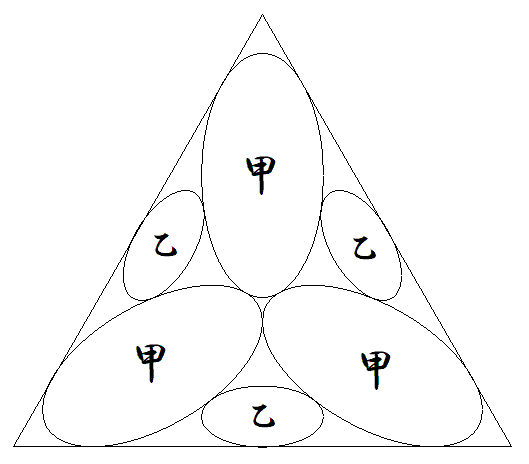 |
|
長軸2a,短軸2bの楕円は,半径Rの大円に短軸の端で接し, 半径rの小円は楕円の長軸の端で接している。 このとき,R,rを求めよ。 | 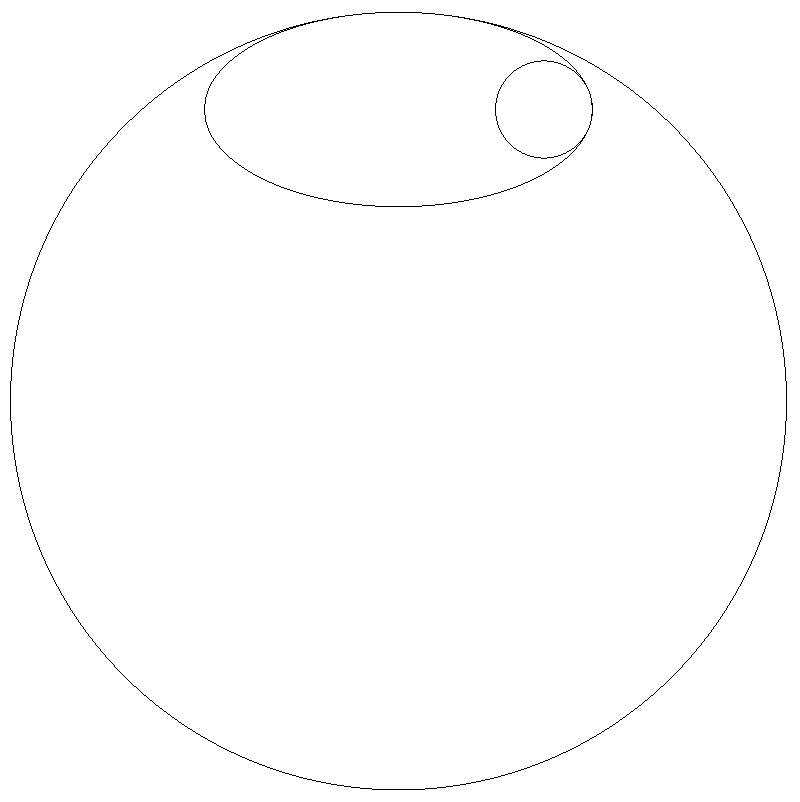 |
|
円内に合同な3個の楕円が図のように配置されている。 3個の楕円の短軸は円の直径上にある。 このとき,長軸÷短軸の値を求めよ。 | 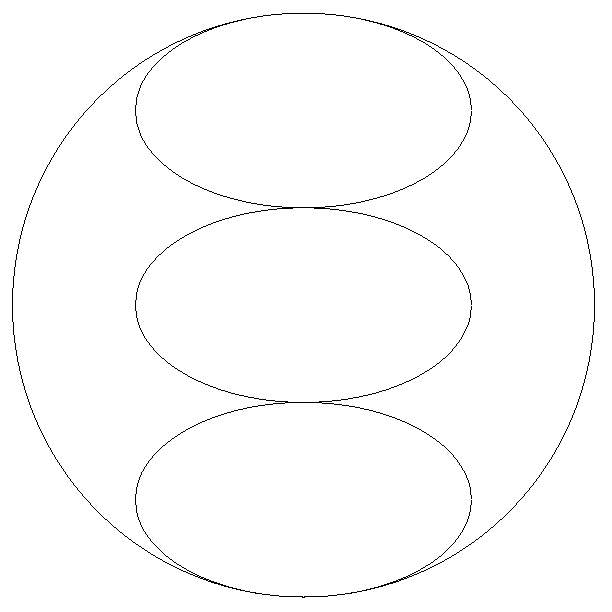 |
|
円内に合同な3個の楕円が図のように配置されている。 上の楕円から順に,短軸,長軸,短軸は,円の直径上に ある。このとき,長軸÷短軸の値を求めよ。 | 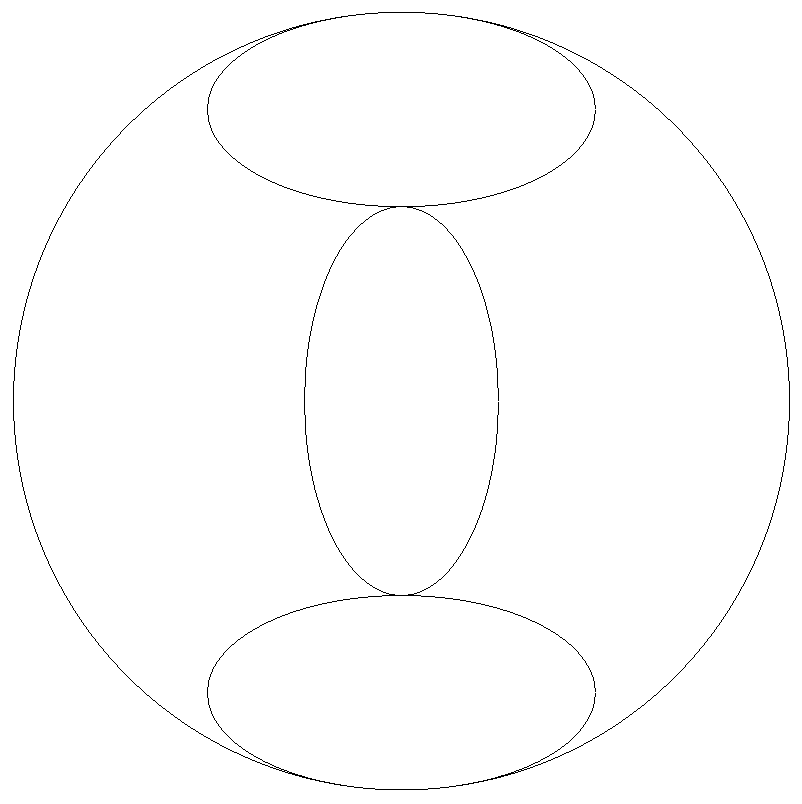 |
|
半径がrの球面上に内角の大きさがA,B,Cで ある球面三角形の面積Sは,S=(A+B+C-π)r2 であることを証明せよ。 | 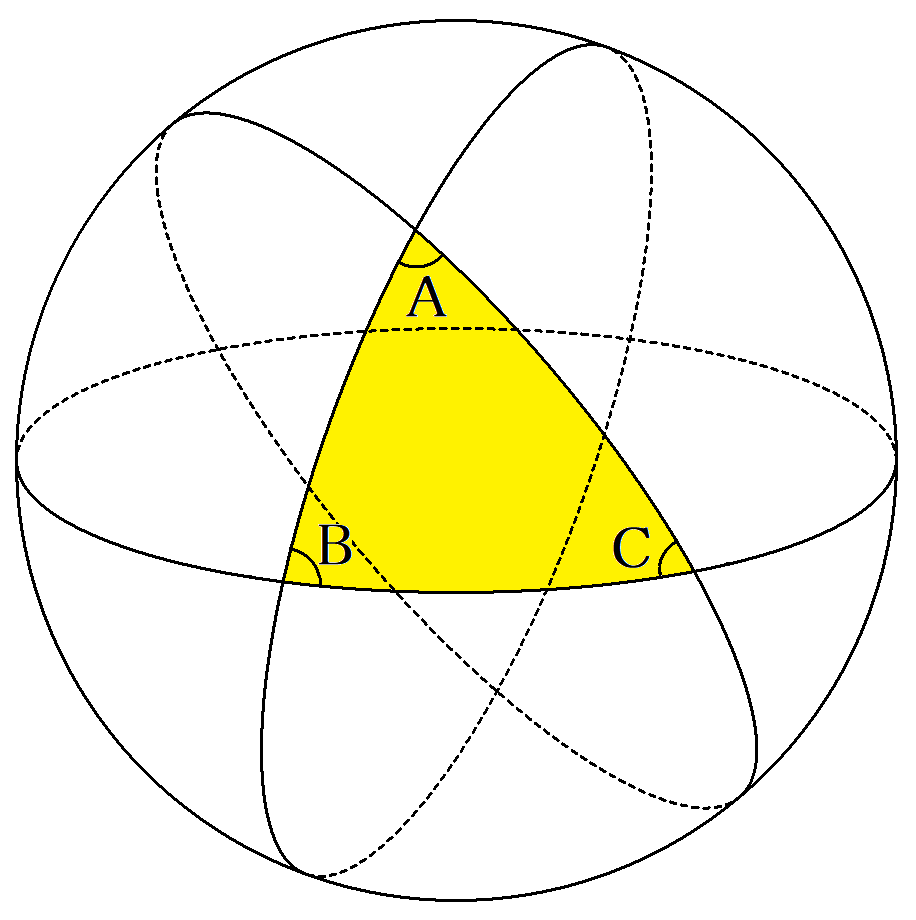 |
aとbの文字を合計n並べる順列で,bが隣り合わない場合の数をanとする。
(1) a1,a2,a3の値を求めよ。
(2) anを求めよ。
|
長方形内に長軸2a,短軸2bの楕円が内接している。 楕円の両軸は長方形の辺に平行である。 半径rの甲円4個が図のように配置されている。 このとき, √(2r)=√a+√b-√(a+b) を証明せよ。 | 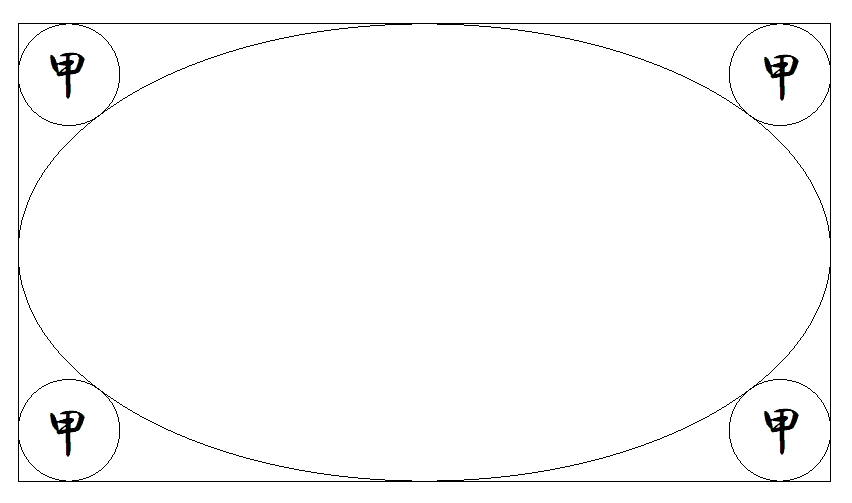 |
|
横2a,縦2bである長方形A1B1C1D1に楕円O1を内接させる。 軸は辺に平行である。 O1に外接し,2辺に接する円のうち∠A1内のものをP1とする。 O1とP1の接点をA2とし,O1に内接し,A2を頂点とする長方形 をA2B2C2D2とする。A2B2∥A1B1である。 長方形A2B2C2D2に楕円O2を内接させる。軸は辺に平行である。 O2に外接し,2辺に接する円のうち∠A2内のものをP2とする。 O2とP2の接点をA3とし,O2に内接し,A3を頂点とする長方形を A3B3C3D3とする。A3B3∥A2B2である。 以下,同様に楕円,円,長方形をつくっていく。 このとき,楕円Onの長軸÷短軸の値を求めよ。 | 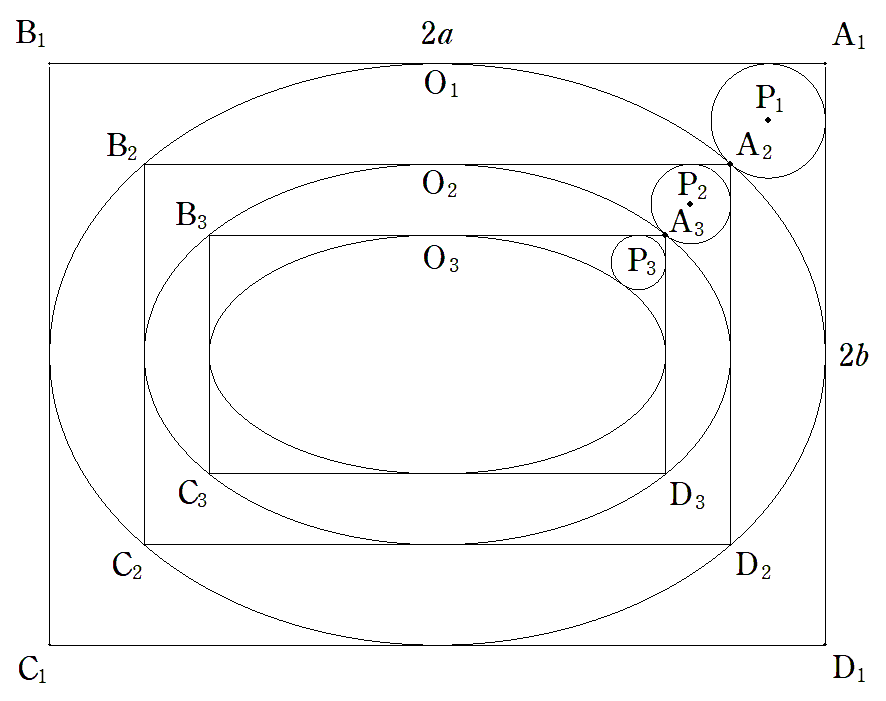 |
|
正六角形の内部に図のように,長軸が2a,短軸が2bである 楕円3個が,長軸が正六角形の対角線に重なるように内接 している。 これら3個の楕円の間に長軸の端で内接し,他方に外接する 6個の等円を描く。 (1) 正六角形の1辺をa,bを用いて表せ。 (2) もし,6個の円が楕円の長軸の端で曲率円(*)ならば, 長軸÷短軸=√{1+2√3cos(π/18)}と表されることを示せ。 (*)半径rの円と長軸2a,短軸2bの楕円の方程式からxまたは yを消去した2次方程式の判別式をDとおくと,D=0となる ときの円を曲率円という。 | 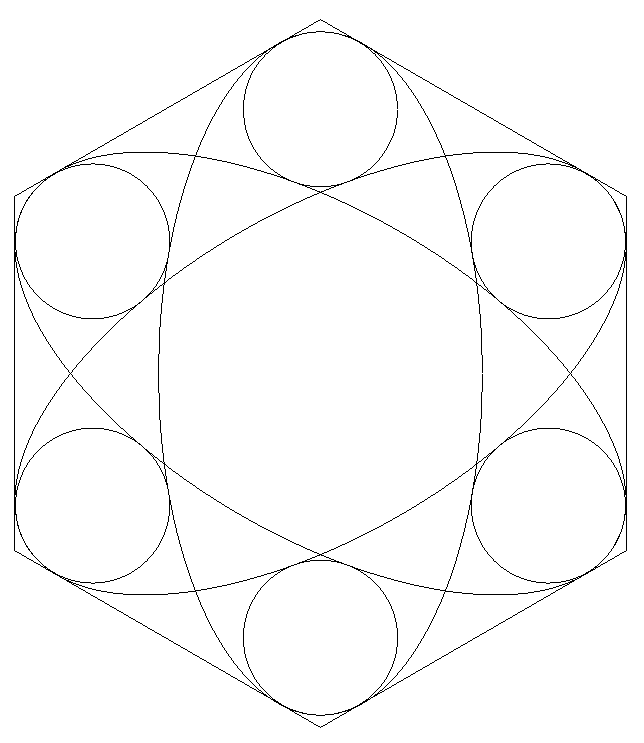 |

|  |

| 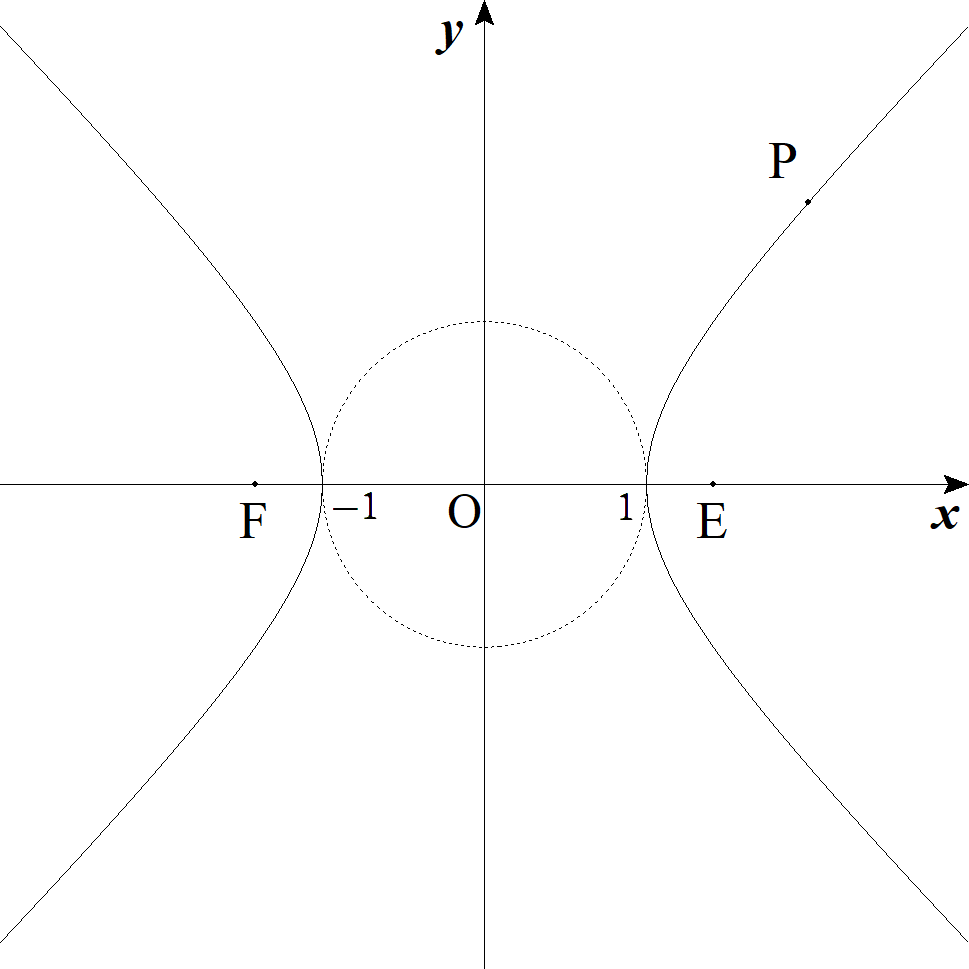 |
曲線y=(x-α)(x-β)(x-γ)とxで囲まれた2つの部分の面積の和Sを,
β-α=p,γ-β=qを用いて表せ。
|
1辺1の正方形の内部に, 図のように甲半円2個, 乙円1個,丙半円2個, 丁円2個が配置されてい る。 丁円の直径を短軸にもつ 楕円の長軸を求めよ。 | 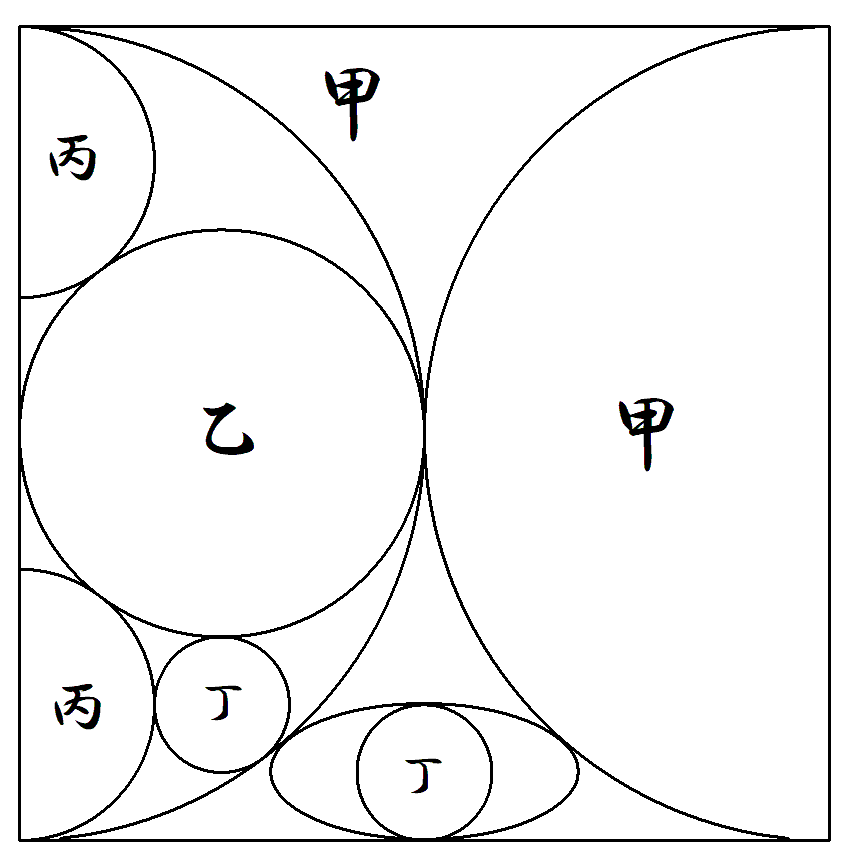 |
|
1辺1の正方形の内部に,4分円弧を図のように2個描き, その内に甲円1個,乙円2個,丙円2個を入れる。 また,軸が正方形の辺に平行な楕円を図のように配置し, その内に丁円1個,戊円2個を入れる。ただし,戊円は 長軸の端で楕円に内接する最大円である。 このとき,各円の半径をそれぞれ求めよ。 | 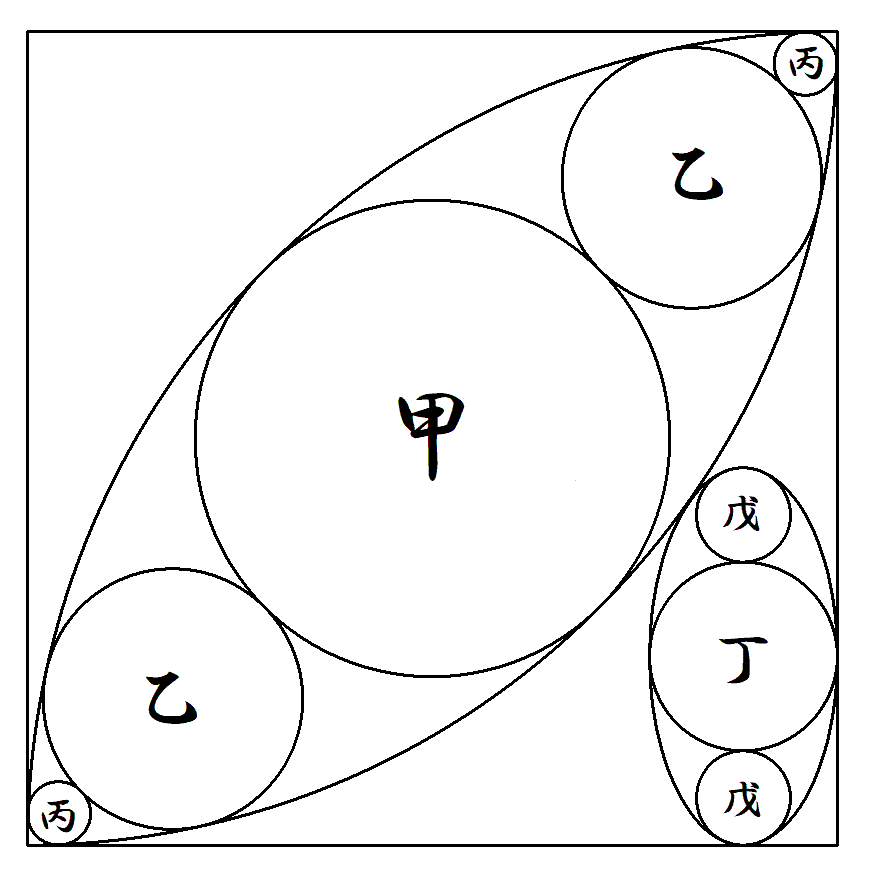 |
|
半円内に相似な甲乙楕円が図のように配置されている。 半円は甲楕円の短軸の端で接する最小半円である。 乙楕円は短軸の端で甲楕円と直径に接している。 このとき,長軸÷短軸の値を求めよ。 | 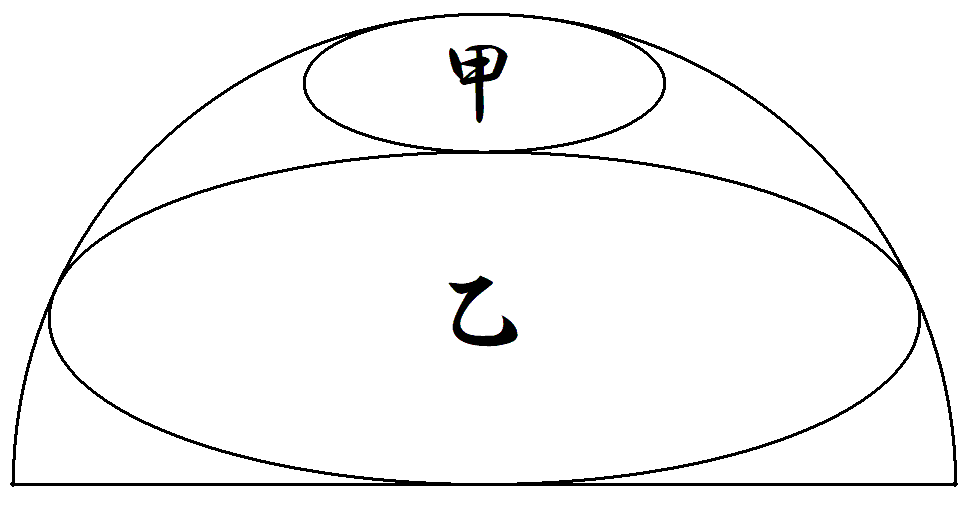 |
|
相似な甲乙丙楕円と円が図のように配置されている。 円は,甲楕円の短軸の端で接する最小円である。 乙丙楕円は円の中心で接している。 丙楕円は短軸の端で円に接している。 このとき,甲乙丙の長軸の比を求めよ。 | 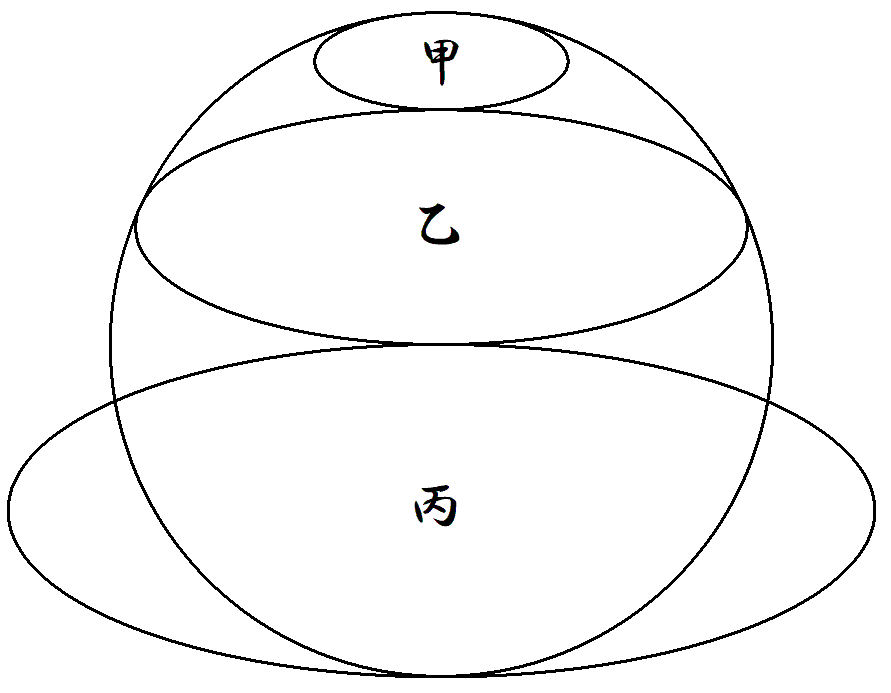 |
|
図のように,軸が正方形の対角線に平行で, 相似である甲乙丙楕円について,甲の長軸, 短軸がそれぞれ2a,2bであるとき,乙丙の 長軸をそれぞれa,bを用いて表せ。 | 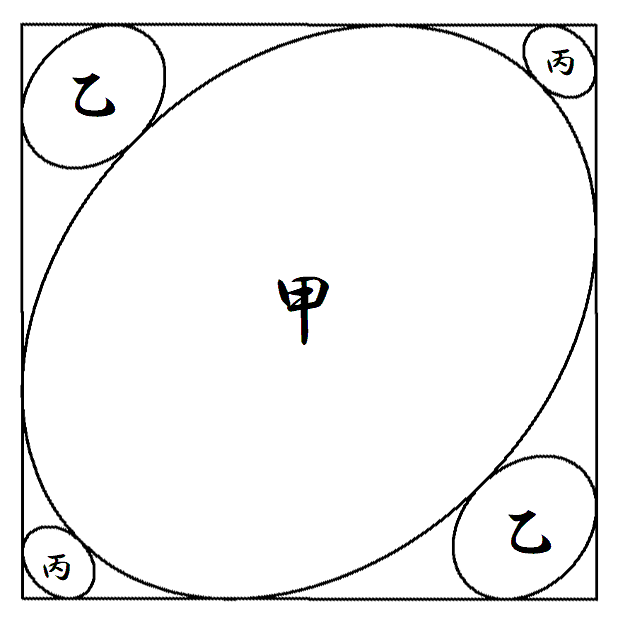 |
|
∠A=90°である直角二等辺三角形ABCのAB,ACの 中点をそれぞれD,Eとする。 相似な甲乙丙楕円が図のように配置されている。 楕円の短軸は,頂点AからBCに下した垂線上にある。 このとき,甲乙丙の長軸の比を求めよ。 | 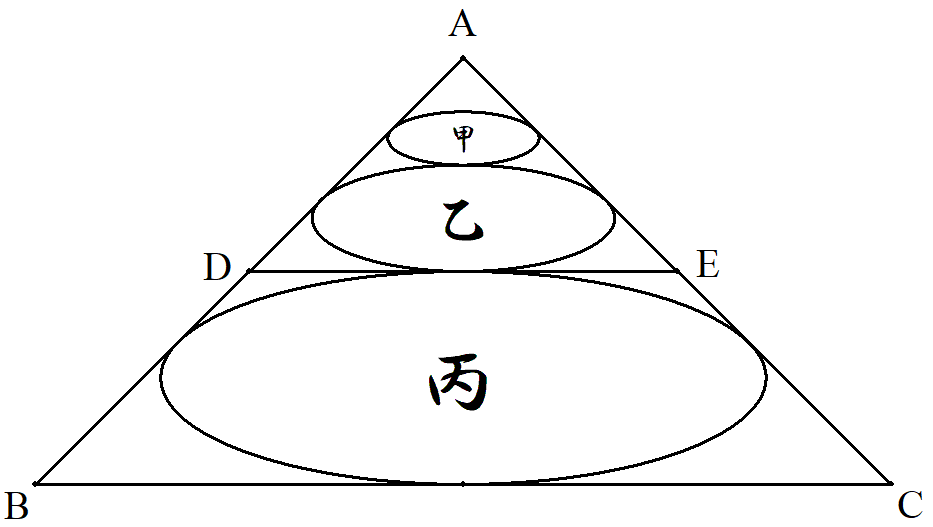 |
|
BC=a,CA=b,∠C=90°である直角三角形ABC内に 軸が直角を挟む2辺に平行な楕円が内接している。 楕円の面積の最大値を求めよ。 | 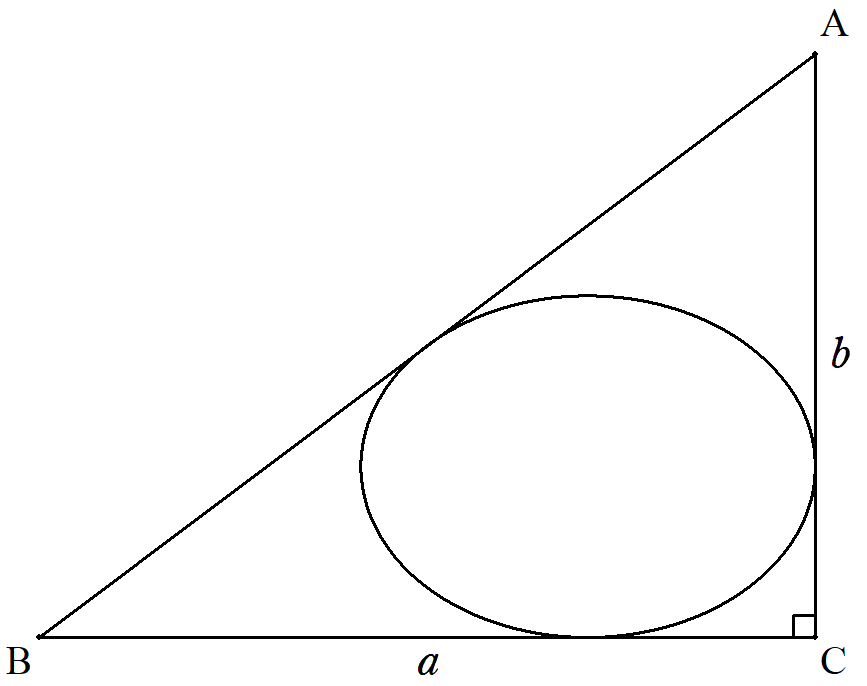 |
|
図のように長方形内に長軸4,短軸2の楕円と 4個の等円が配置されている。ただし,楕円の 両軸は長方形の辺に平行である。 このとき,長方形の横の長さを求めよ。 | 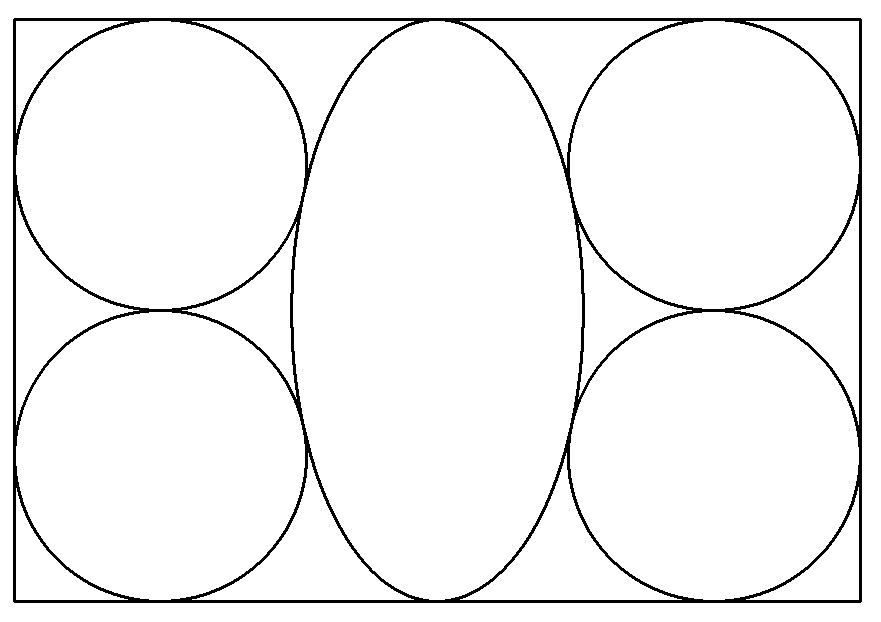 |
|
図のように長方形内に長軸4,短軸2の楕円と 4個の等円が配置されている。ただし,楕円の 両軸は長方形の辺に平行である。 このとき,長方形の横の長さを求めよ。 | 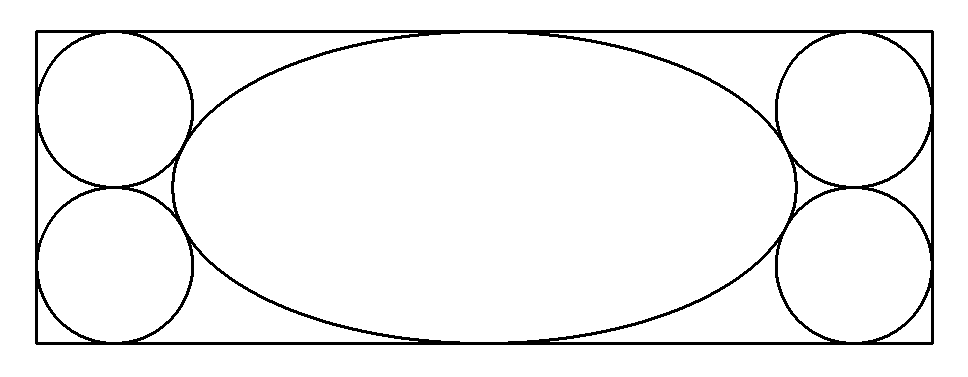 |
|
長軸2a,短軸2bの楕円内に.図のように 6個の等円が内接している。ただし,等円は 長軸,短軸の端で楕円に接する最大円である。 このとき,長軸÷短軸の値を求めよ。 | 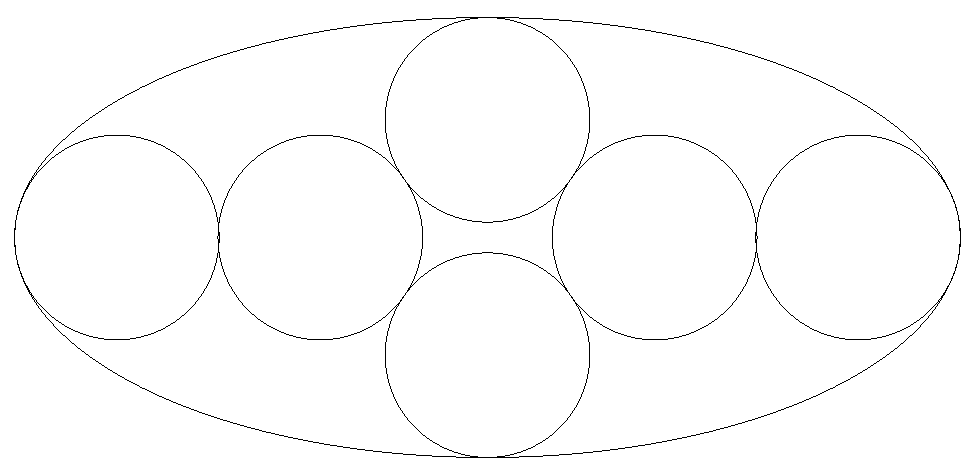 |
|
1辺の長さが1である正三角形内に2本の斜線を引き, 図のように,甲円1個,乙円3個を内接させる。 甲円の半径を求めよ。 | 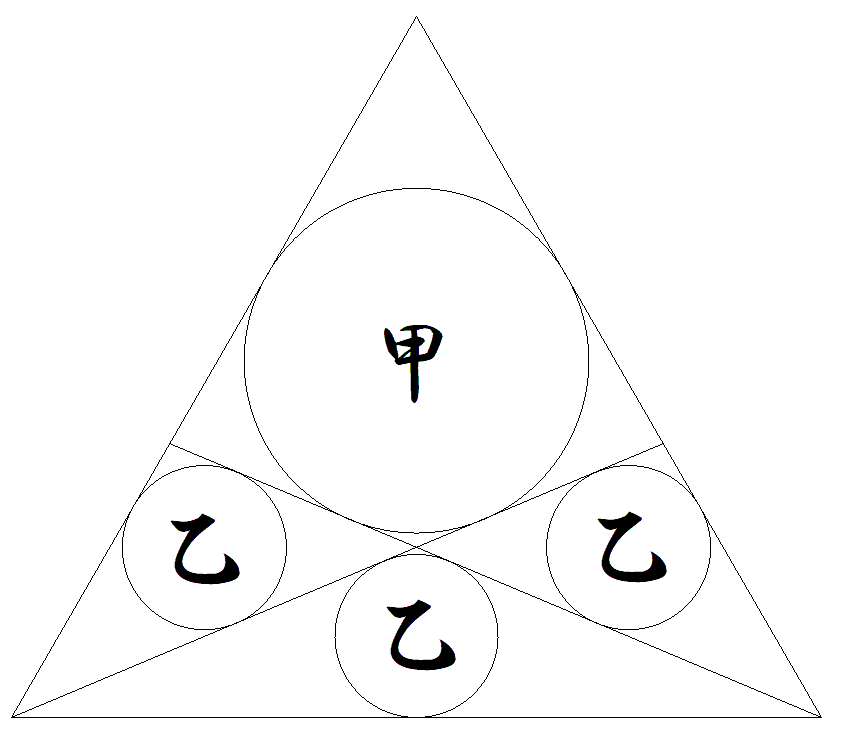 |