■趣味の数学問題集・Ｂ問題

  1. 大小の楕円は相似で，大楕円の長軸と
    小楕円の軸は重なっている。このとき，
    長軸÷短軸の値を求めよ。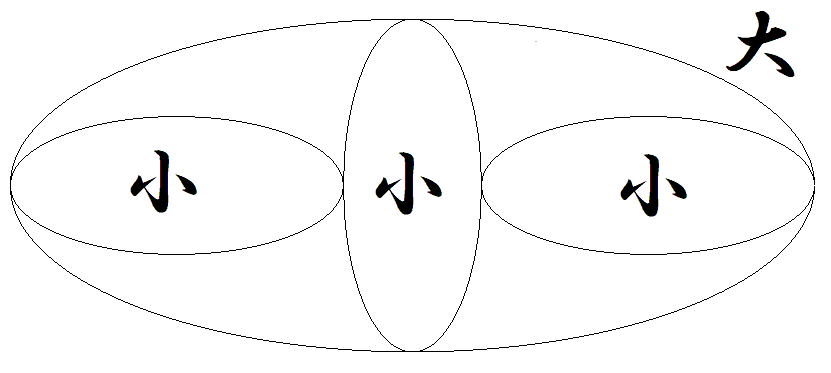



  2. 等辺が1である直角二等辺三角形内に
    2本の斜線を引き，図のように甲円1
    個，乙円3個を内接させる。
    このとき，甲円の半径を求めよ。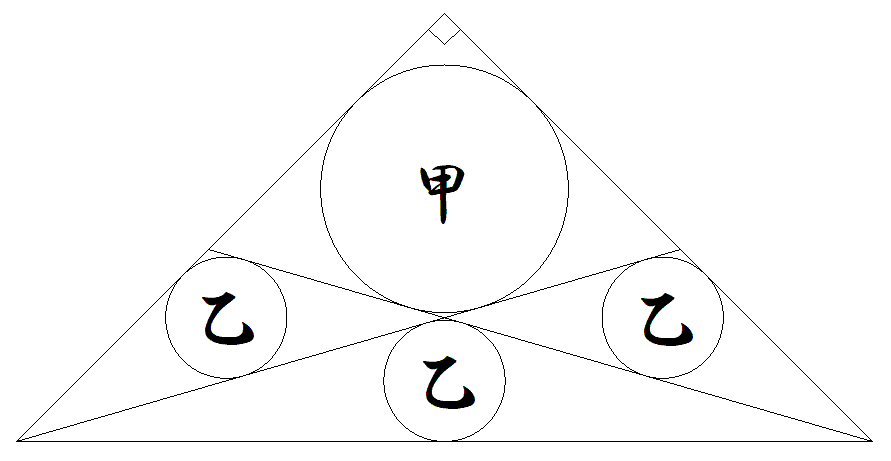



  3. 図のように，短軸が2である楕円内に2個の甲円
    と正三角形とその内接円乙が配置されている。
    甲円は長軸の端で接する最大円で正三角形に接し
    ている。
    正三角形の頂点は，短軸の端にあり，その対辺は
    長軸に平行である。
    このとき，甲乙円の半径をそれぞれ求めよ。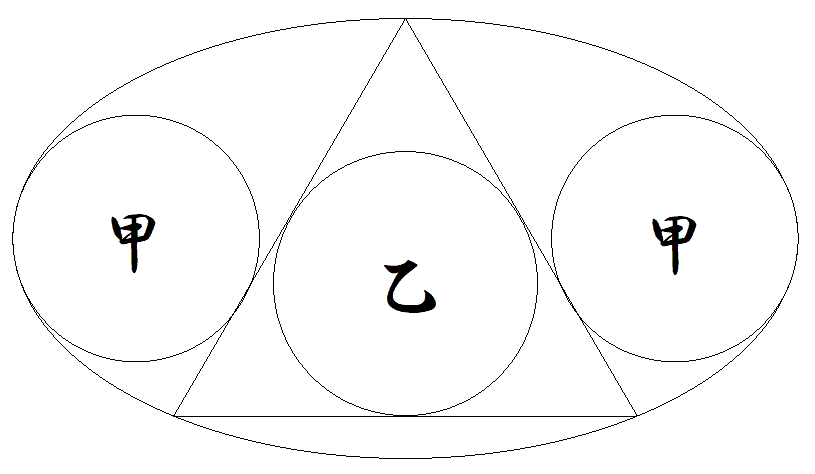



  4. 図のように，短軸が2である楕円内に2個の甲円
    と正方形とその内接円乙が配置されている。
    甲円は長軸の端で接する最大円で正方形に接し
    ている。
    正方形の辺は軸に平行である。
    このとき，甲乙円の半径をそれぞれ求めよ。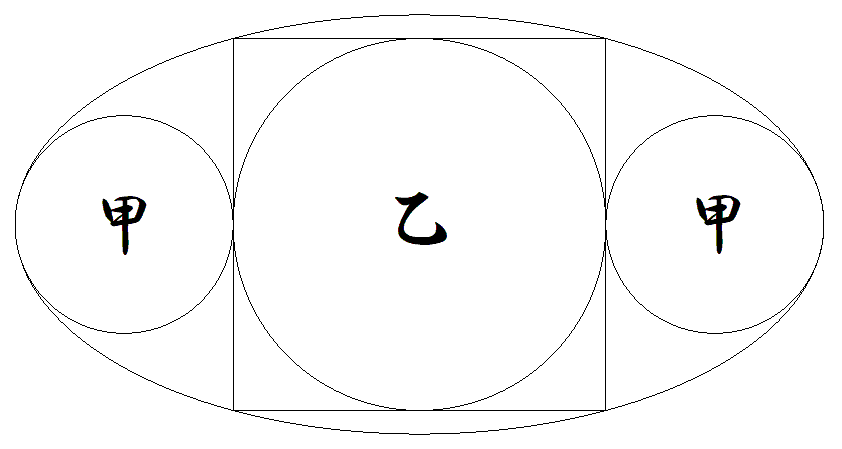



  5. 長軸2a，短軸2bである楕円に図のように正五角形
    ABCDEが内接している。Aは短軸の端の点で，C，
    Dは楕円上の点で，CDは長軸に平行である。
    このとき，正五角形の1辺を求めよ。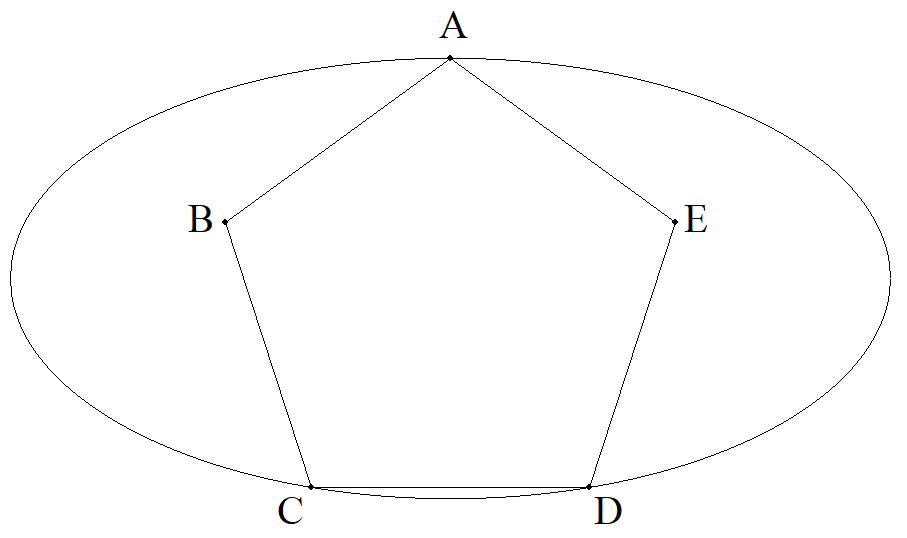



  6. 図のように，短軸が2である楕円内に2個の甲円
    と正五角形ABCDEとその内接円乙が配置されて
    いる。
    甲円は長軸の端で接する最大円で正五角形に接
    している。
    Aは短軸の端の点で，CDは長軸に平行である。
    このとき，甲乙円の半径の近似値をそれぞれ求
    めよ。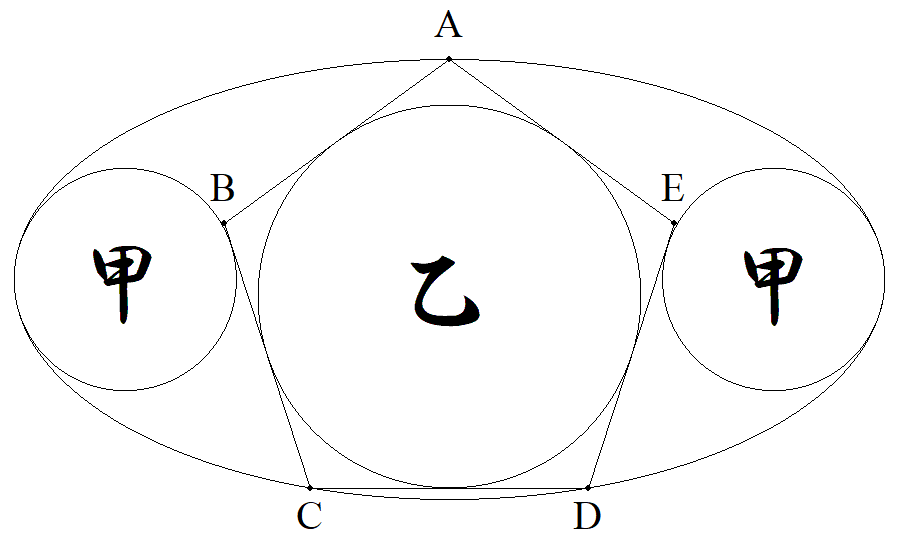



  7. 図のように，短軸が2である楕円内に2個の甲円
    と正六角形ABCDEFとその内接円乙が配置され
    ている。
    甲円は長軸の端で接する最大円で正六角形の辺
    BC，EFに接している。
    正六角形の頂点A，Dは短軸の端の点である。
    このとき，甲乙円の半径をそれぞれ求めよ。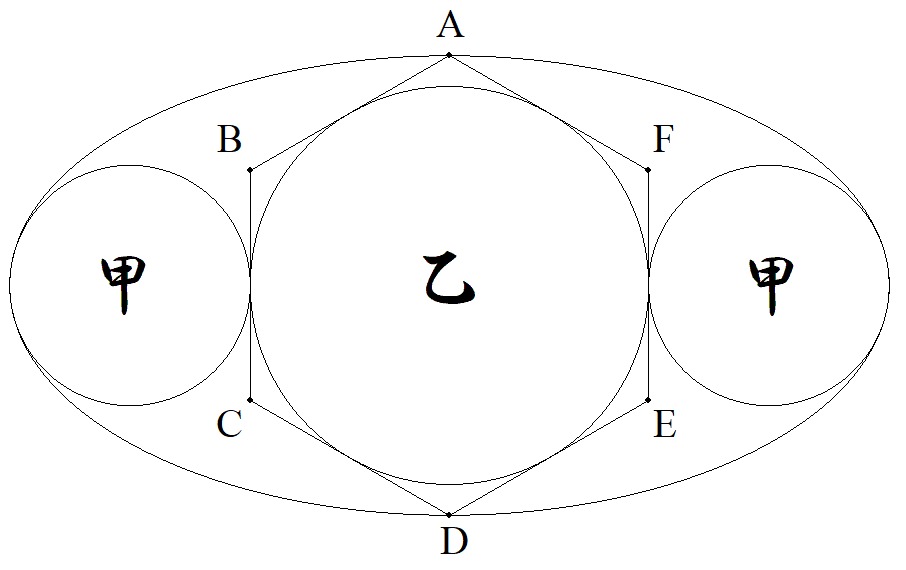



  8. 図のように，短軸が2である楕円内に2個の甲円
    と正六角形ABCDEFとその内接円乙が配置され
    ている。
    甲円は長軸の端で接する最大円で正六角形の頂
    点C，Fを通る。
    正六角形の頂点A，B，D，Eは楕円上にあり，
    C，Fは長軸上にある。
    このとき，甲乙円の半径をそれぞれ求めよ。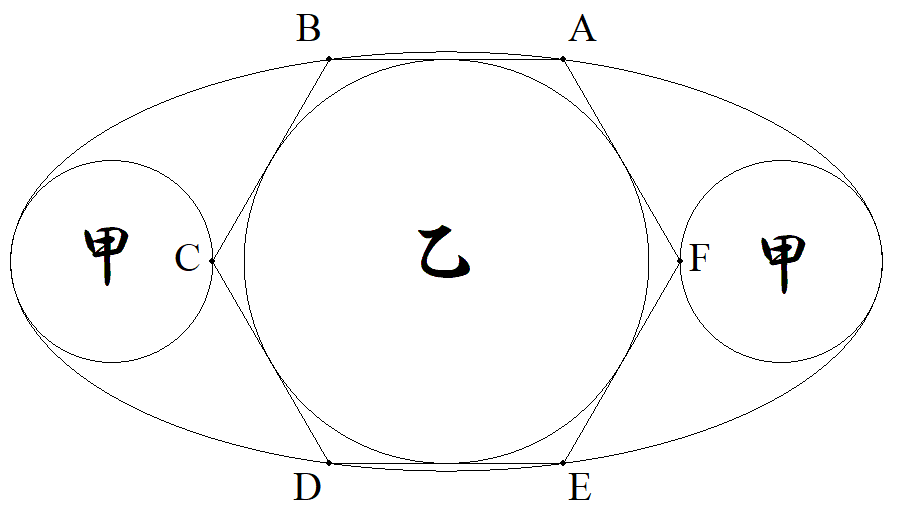



  9. 楕円の軸の端で接する4個の等円は最大円である。
    しかも，長軸の端で接する2個の円と短軸の端で
    接する1個の円は1点で交わっている。
    このとき，長軸÷短軸の値を求めよ。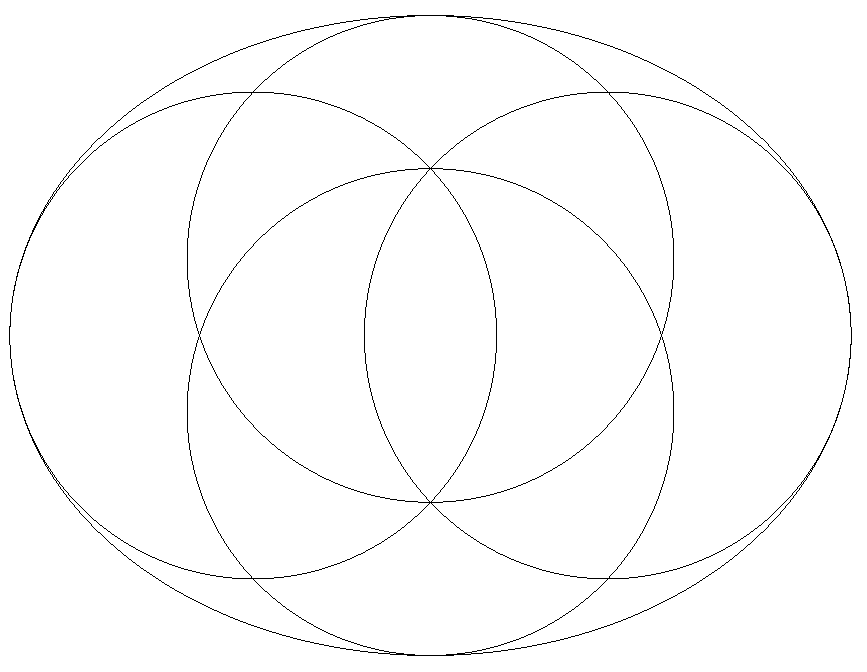



  10. 図のように，楕円内に2個の甲円と正方形ABCD
    とその内接円乙が配置されている。
    甲円は長軸の端で接する最大円で，頂点B，Dを
    通る。
    正方形の頂点A，Cは短軸の端の点で，B，Dは
    長軸上にある。
    このとき，甲円2個と乙円の面積は等しくなる
    ことを証明せよ。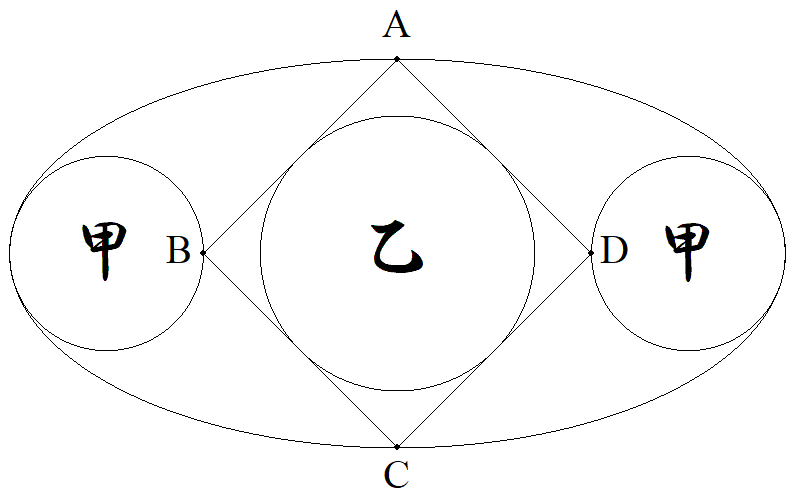



  11. 楕円の軸の端に内接する4個の等円は最大円である。
    その4個の等円の中心を頂点にもつひし形に内接する
    円も等円になる。長軸÷短軸の値をtとするとき，tの
    満たす方程式を求めよ。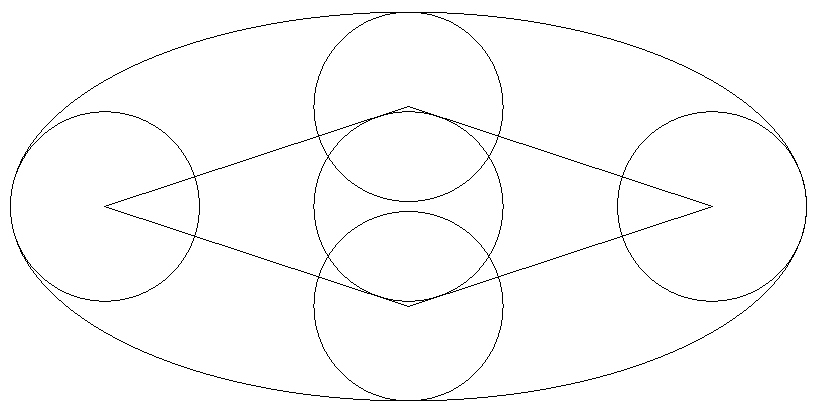



  12. 楕円の中心を通る2本の斜線を引き，図のよう
    に楕円の軸の端に内接する4個の等円を入れる。
    ただし，円は最大円である。
    このとき，長軸÷短軸の値をtとするとき，tの
    満たす方程式を求めよ。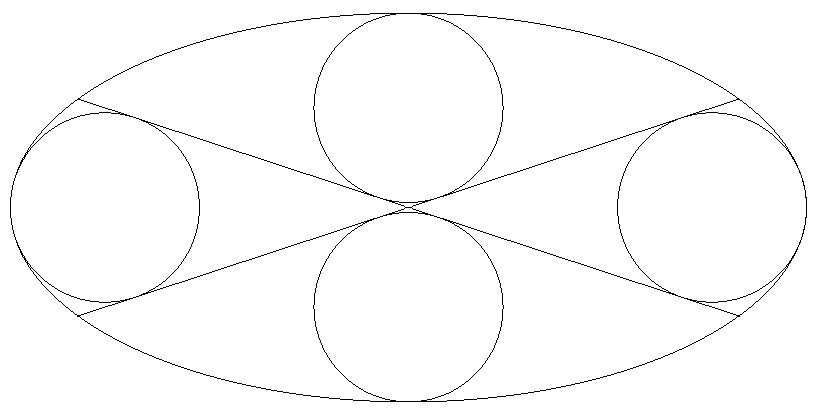



  13. 楕円の中心を通る2本の斜線を引き，楕円と斜線に
    接する4個の等円を入れる。
    ただし，円は楕円の軸の端で接する最大円である。
    このとき，4個の等円の中心を頂点にもつひし形に
    内接する円も等円になることを証明せよ。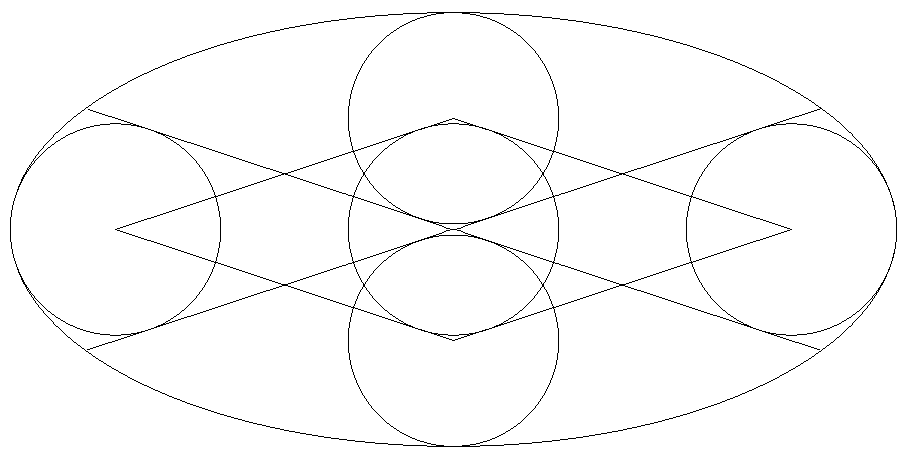



  14. 大円内に3個の合同な楕円と4個の合同な小円が
    図のように配置されている。
    中央の小円は大円と同心円で，楕円の長軸の端
    で接する最大円で，他の小円は大円と2個の楕円
    に接している。
    このとき，大円径÷小円径の値を求めよ。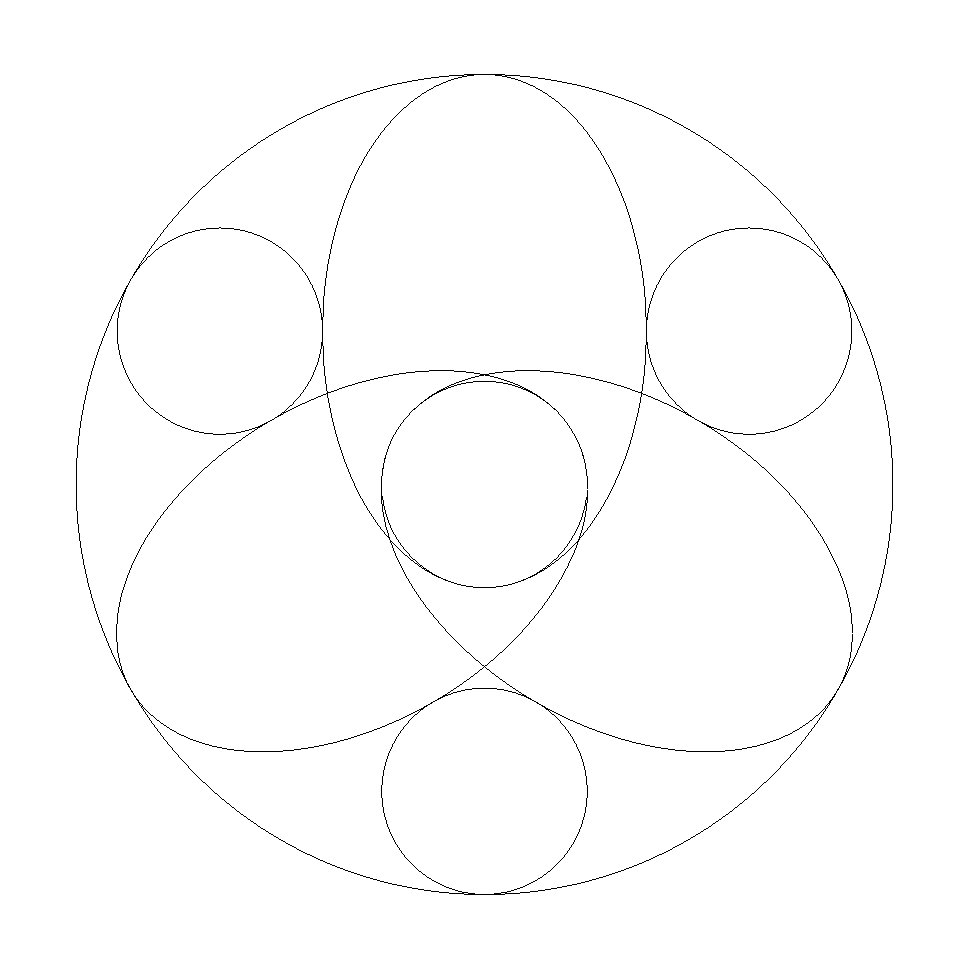



  15. 大円内に4個の合同な楕円と5個の合同な小円が
    図のように配置されている。
    中央の小円は大円と同心円で，楕円の長軸の端
    で接する最大円で，他の小円は大円と2個の楕円
    に接している。
    このとき，大円径÷小円径の値をkとするとき，
    kの満たす4次方程式を1つ求めよ。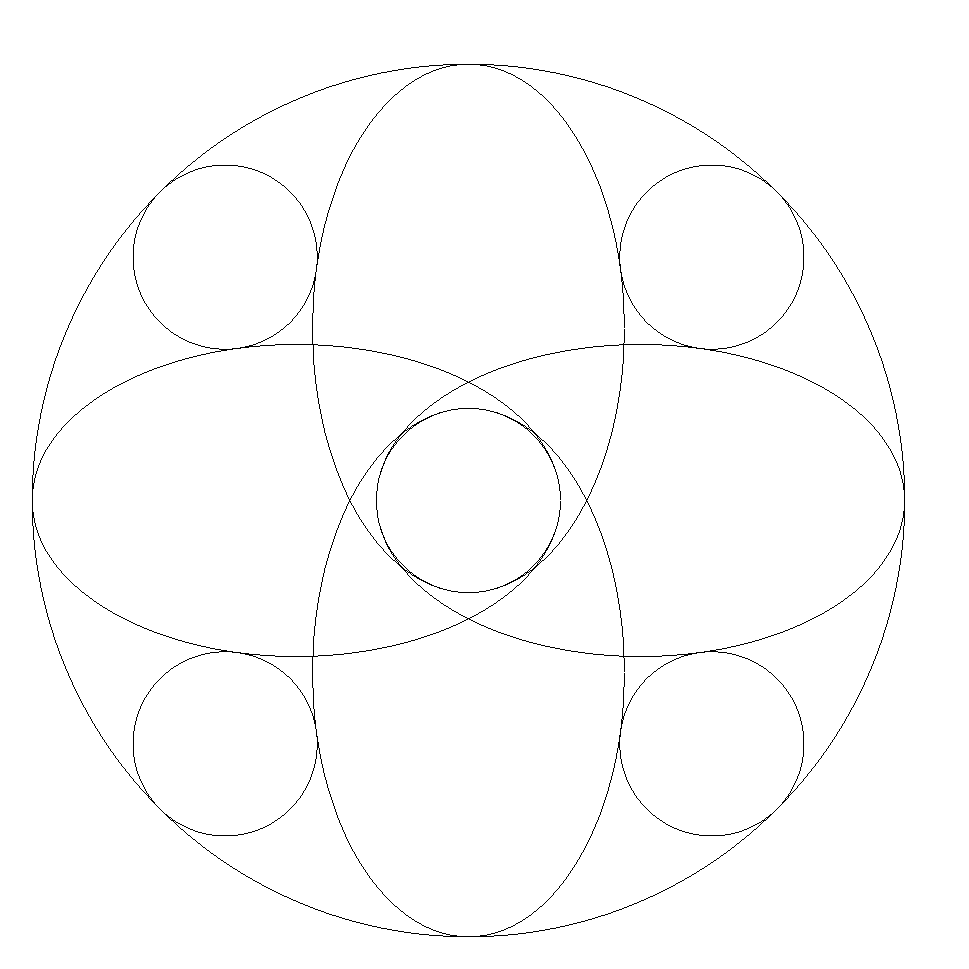



  16. 大円内に6個の合同な楕円と3個の合同な小円が
    図のように配置されている。
    6個の楕円の長軸の端点は正六角形をなす。
    中央の小円は大円と同心円で，楕円の長軸の端
    で接する最大円で，他の小円は大円と2個の楕円
    に接している。
    このとき，大円径÷小円径の値をkとするとき，
    kの満たす4次方程式を1つ求めよ。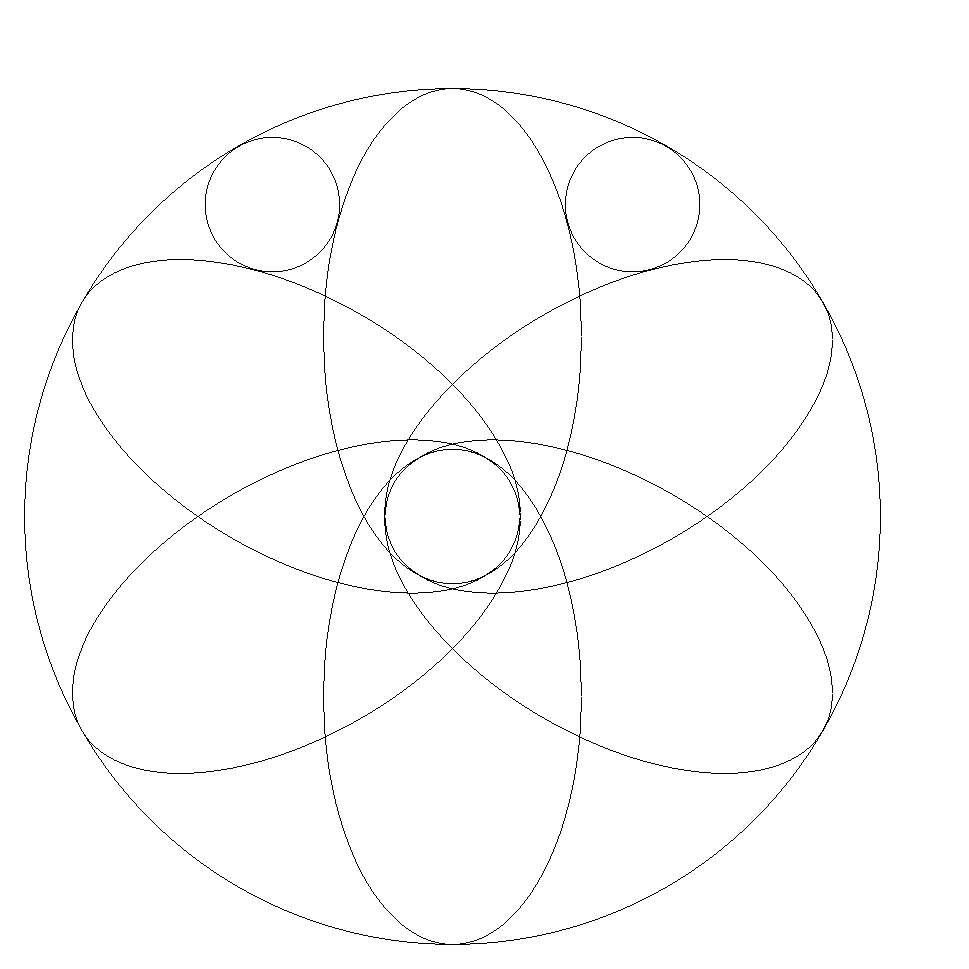



  17. 図のように，正三角形内に長軸が中線上にある3個
    の合同な楕円と4個の等円が配置されている。
    中央の円は楕円の長軸の端で接する最大円である。
    他の3個の円は正三角形と2個の楕円に接している。
    このとき，長軸÷短軸の値をtとし，tの満たす整
    方程式を1つ求めよ。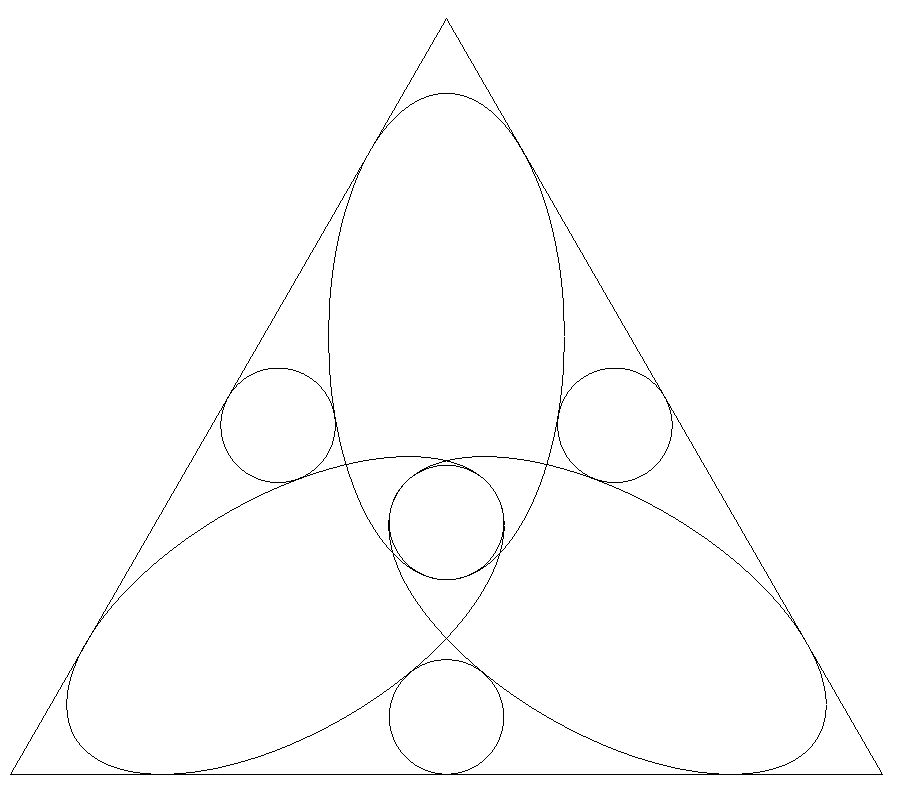



  18. 長軸2a，短軸2bの楕円に2点で接する半径rの円がある。
    楕円と円の中心間の距離cを求めよ。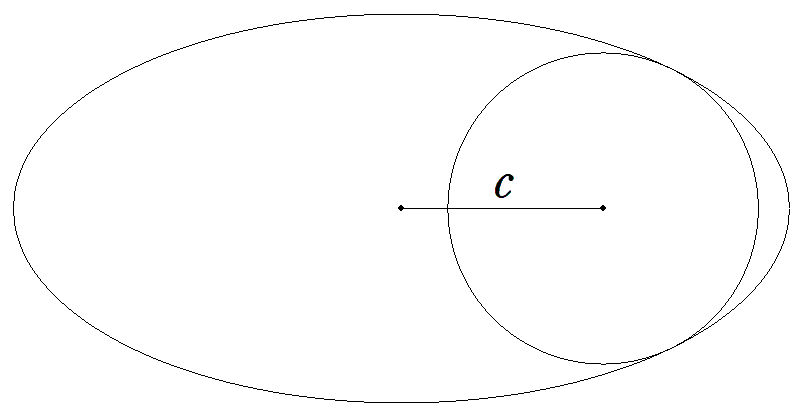



  19. 長軸2a，短軸2bの楕円の長軸の端における接線と
    楕円と点T(p，q)で接する半径rの円がある。
    rをa，b，pで表せ。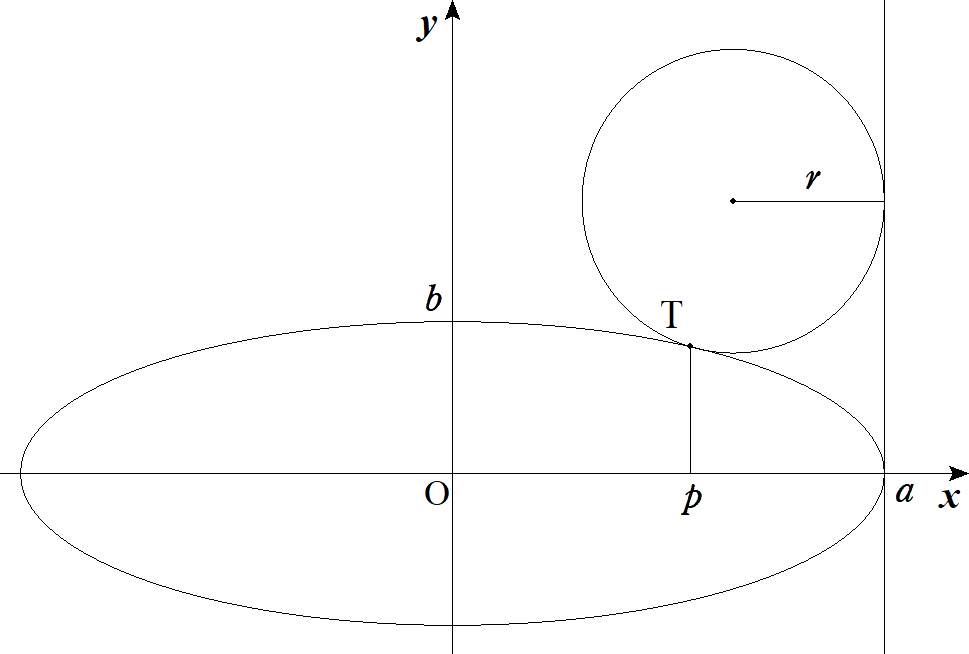



  20. 図のように楕円内に甲円2個，乙円4
    個が配置されている。
    甲円は長軸の端で接する最大円である。
    乙円は甲円と長軸，短軸に接している。
    このとき，長軸÷短軸の値を求めよ。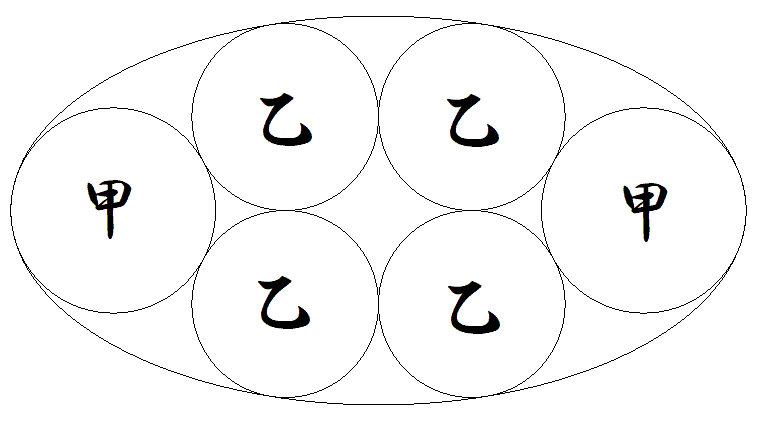



  21. 2個の楕円と1個の大円と8個の小円が図の
    ように配置されている。
    大円に外接する小円は，長軸の端で接す
    る最大円である。
    大円に内接する小円は，2個の楕円に接
    している。
    大円，小円の半径をそれぞれR，r，R/r＝
    kとおくとき，kの満たす整係数の方程式を
    一つ求めよ。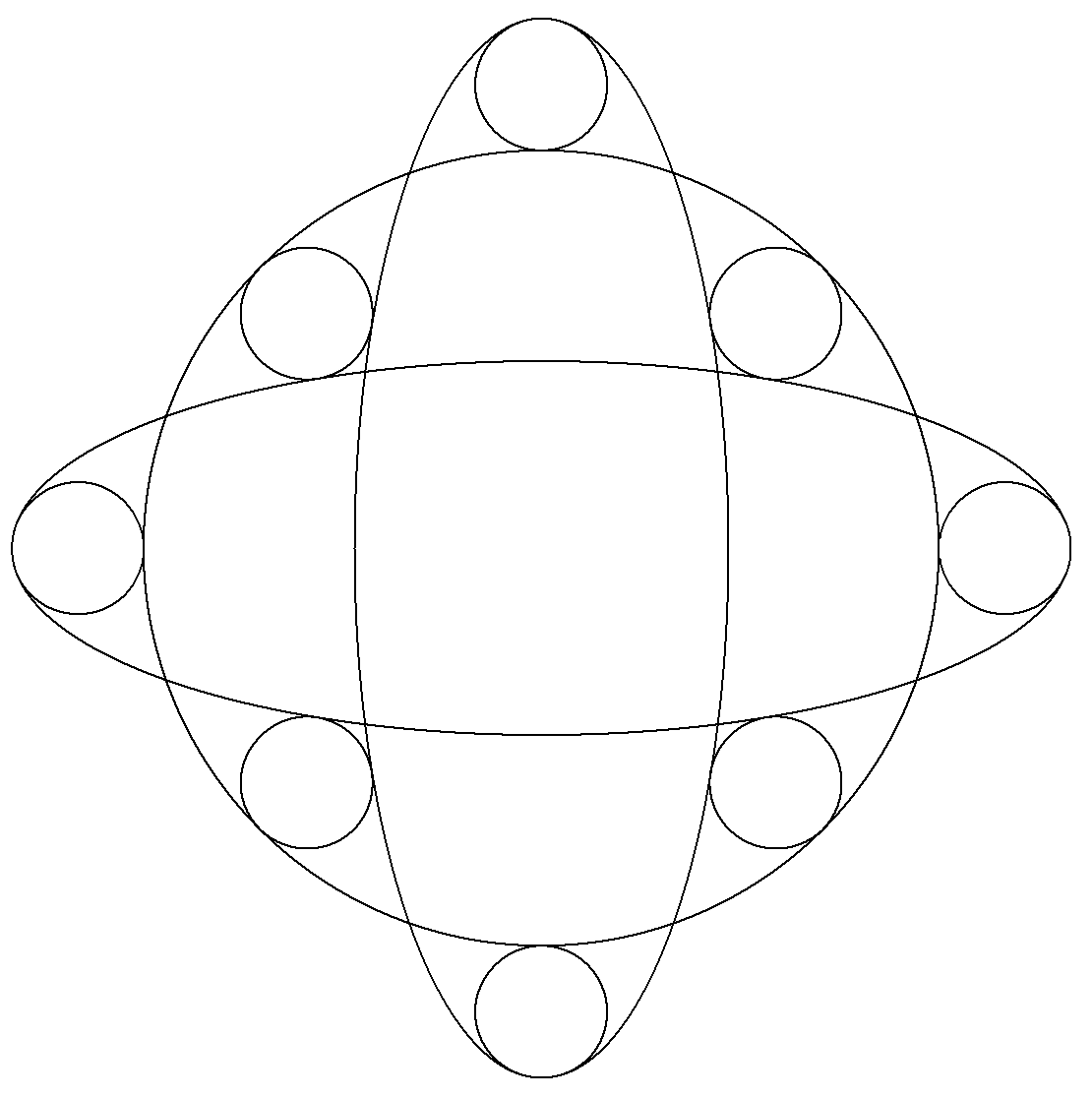



  22. 図のように，楕円と大円は同心で，4個の小円は等円である。
    大円に外接する小円は，長軸の端で接する最大円である。
    大円に内接する小円は，短軸の端で接している。
    大円，小円の半径をそれぞれR，rとおくとき，R/rの値を求めよ。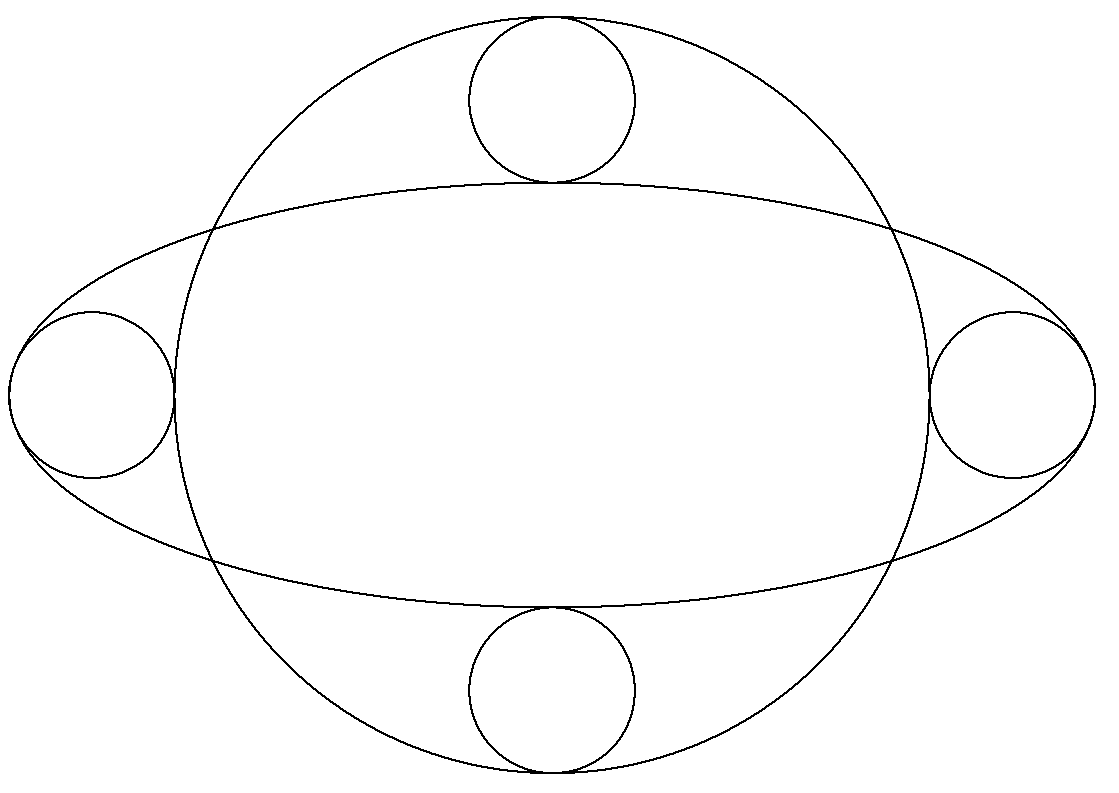



  23. 図のように，正方形と楕円と4個の等円が配置されている。
    正方形の対角線は楕円の軸に重なっている。
    楕円に内接する円は，長軸の端で接する最大円である。
    楕円に外接する円は，短軸の端で接し，2辺に接している。
    このとき，長軸÷短軸の値を求めよ。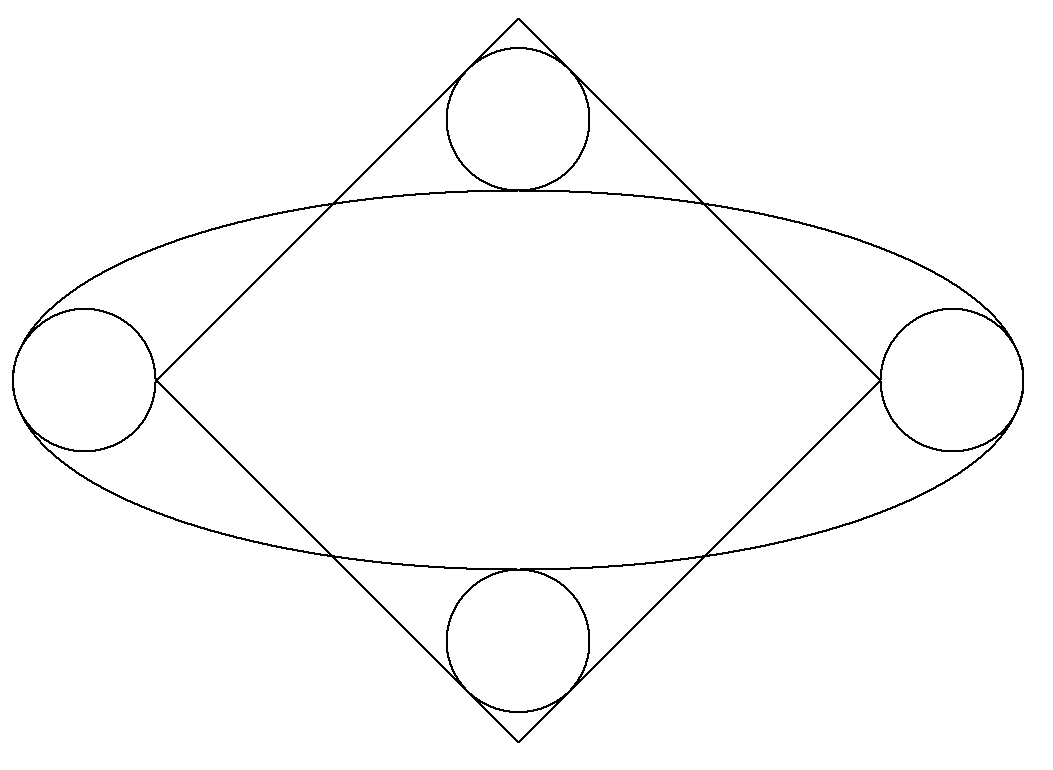



  24. 正三角形と楕円と3個の等円が図のように配置されている。
    楕円の長軸は底辺に平行で短軸の端で底辺に接している。
    楕円に内接する円は，長軸の端で接する最大円で，辺に接している。
    楕円に外接する円は，2辺に接している。
    このとき，長軸÷短軸の値を求めよ。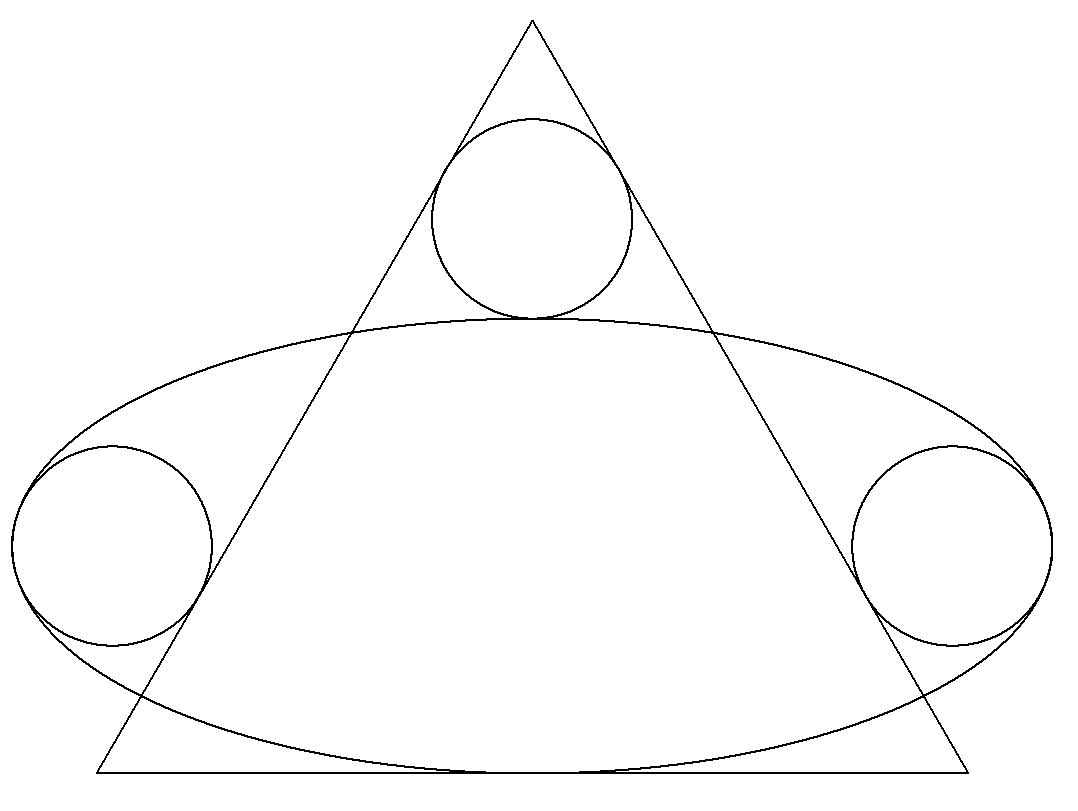



  25. 3個の楕円と大円は同心である。7個の小円は等円である。
    大円に外接する小円は，楕円の長軸の端で接する最大円
    である。
    大円に内接する小円は，2個の楕円に接している。
    大円，小円の半径をそれぞれR，r，R/r=kとおくとき，
    kの満たす整係数の方程式を一つ求めよ。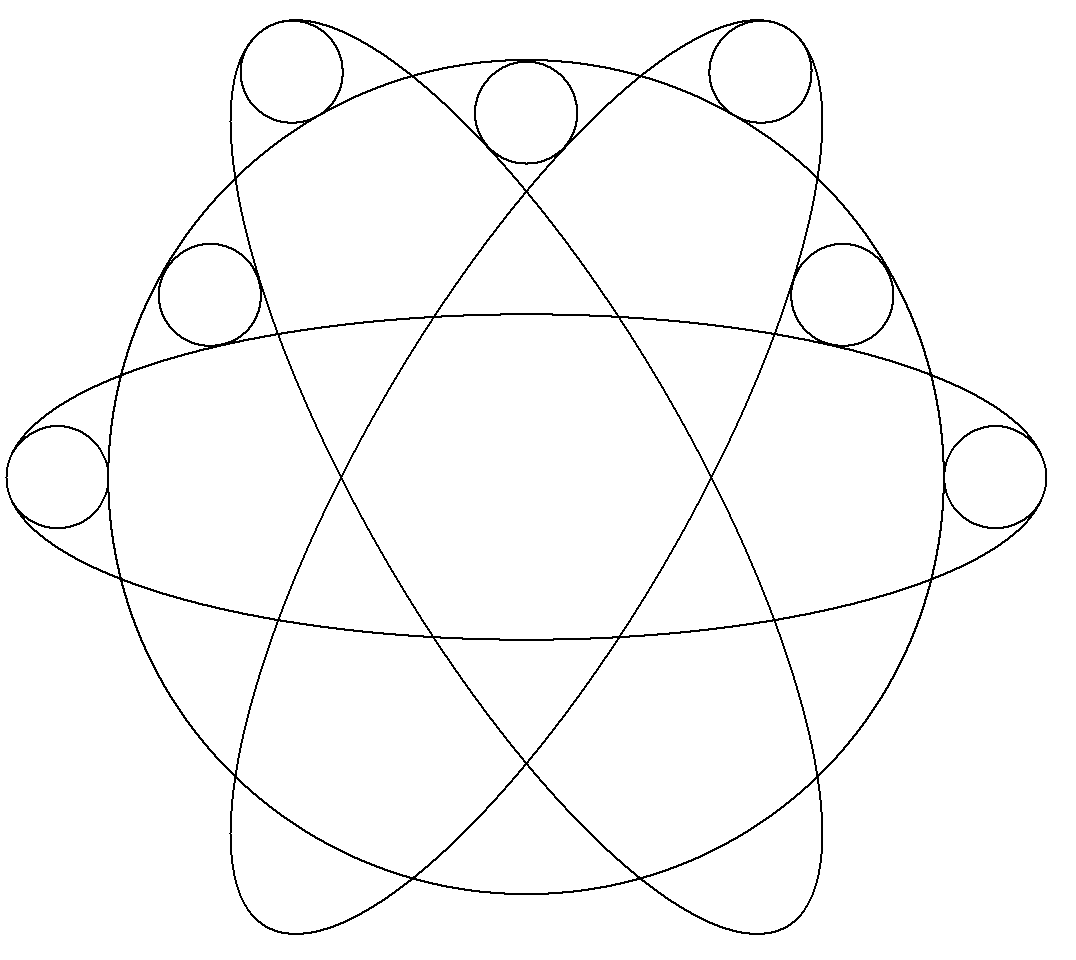



  26. 正五角形と楕円と4個の等円が，図のように配置されている。
    楕円に内接する円は，長軸の端で接する最大円で，辺に接し
    ている。
    楕円に外接する円は，短軸の端に接していて，辺に接している。
    このとき，長軸÷短軸の値を求めよ。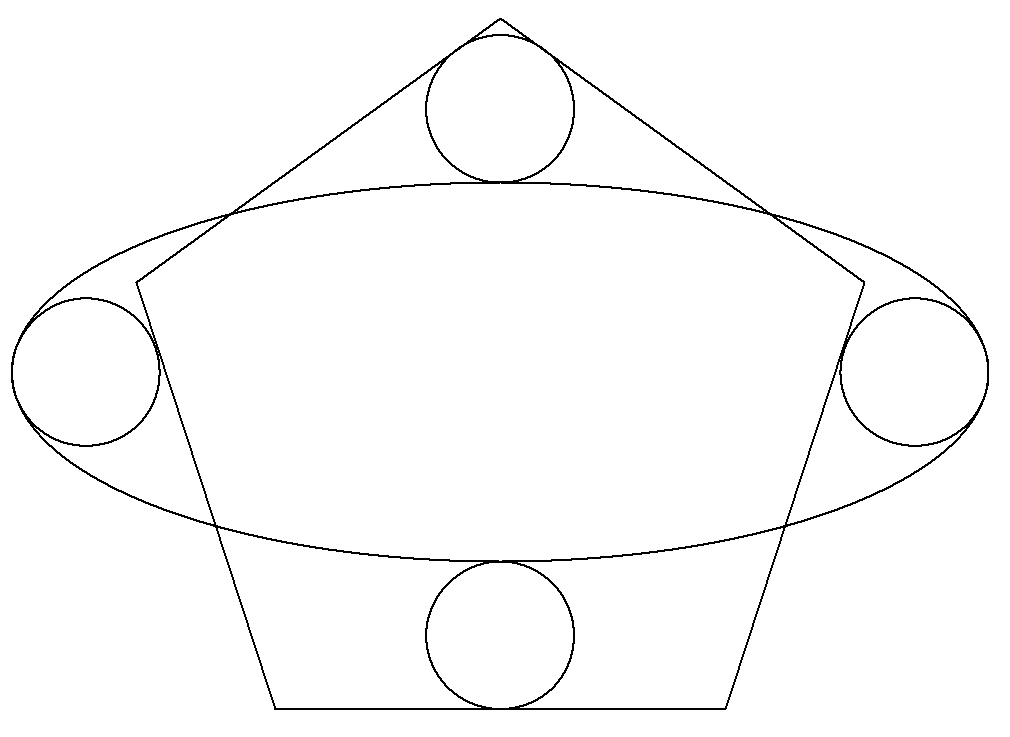



  27. 正六角形と楕円と4個の等円が図のように配置されている。
    楕円に内接する円は，長軸の端で接する最大円で，辺に接
    している。
    楕円に外接する円は，短軸の端で接し，2辺に接している。
    このとき，長軸÷短軸の値を求めよ。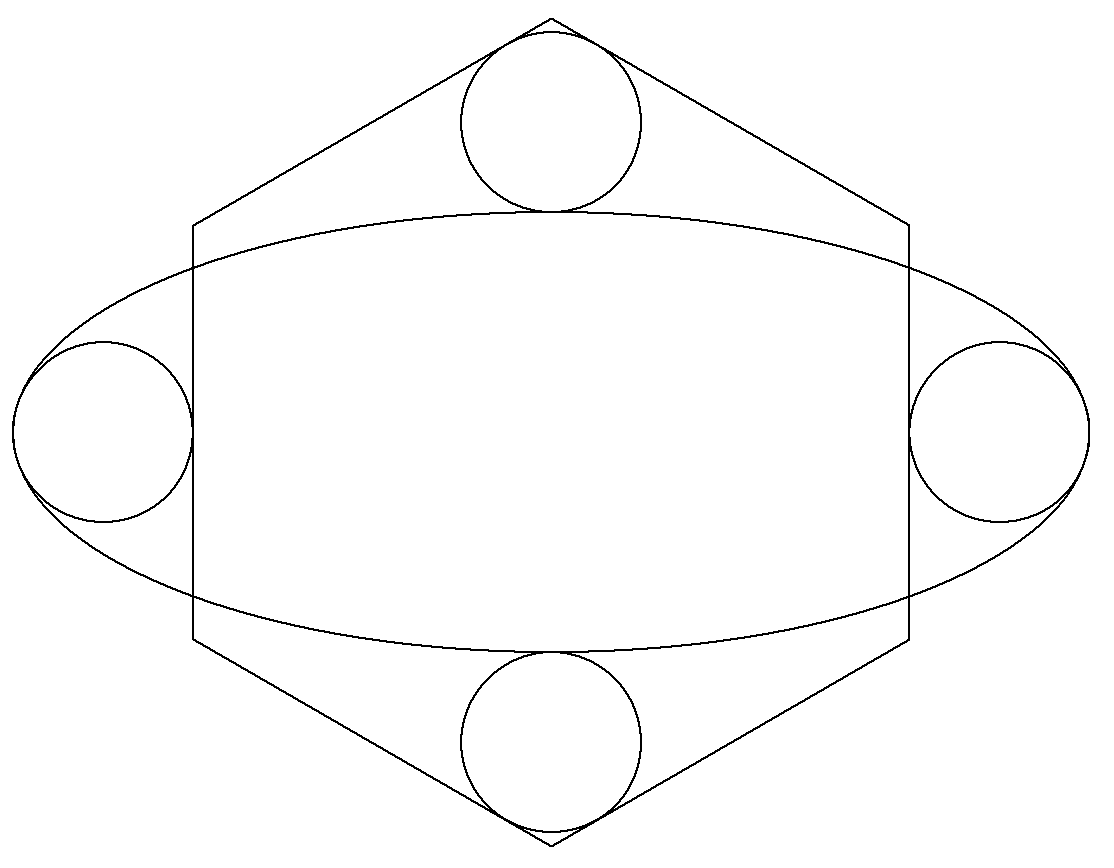



  28. 正三角形と楕円と4個の等円が図のように配置されている。
    楕円の長軸は底辺に平行である。
    楕円に内接する円は，長軸の端で接する最大円で，辺に
    接している。
    楕円に外接する円は，短軸の端で接し，辺に接している。
    このとき，長軸÷短軸の値を求めよ。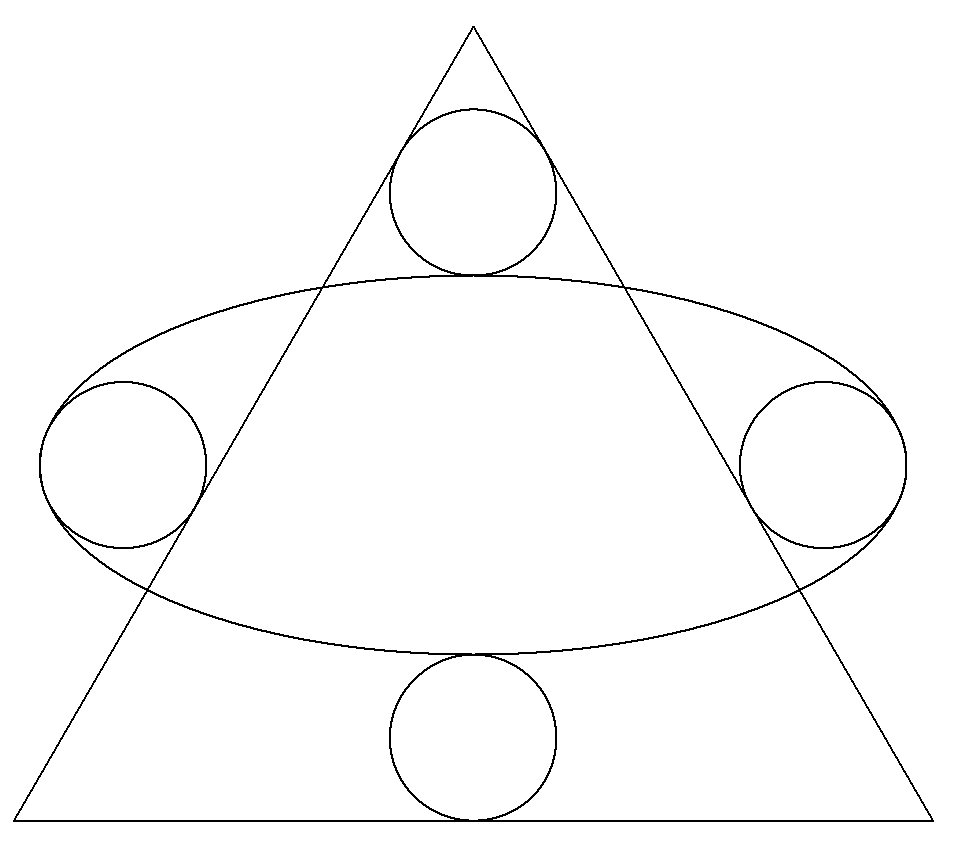



  29. 正n角形と大円と甲円と(n+2)個の乙円が，
    図のように配置されている。
    甲円は，辺の中点と大円に内接している。
    甲円の両隣の乙円は，甲円と辺と大円に内接している。
    他のn個の乙円は2辺と大円に外接している。
    このとき，甲円径÷乙円径の値tを求めよ。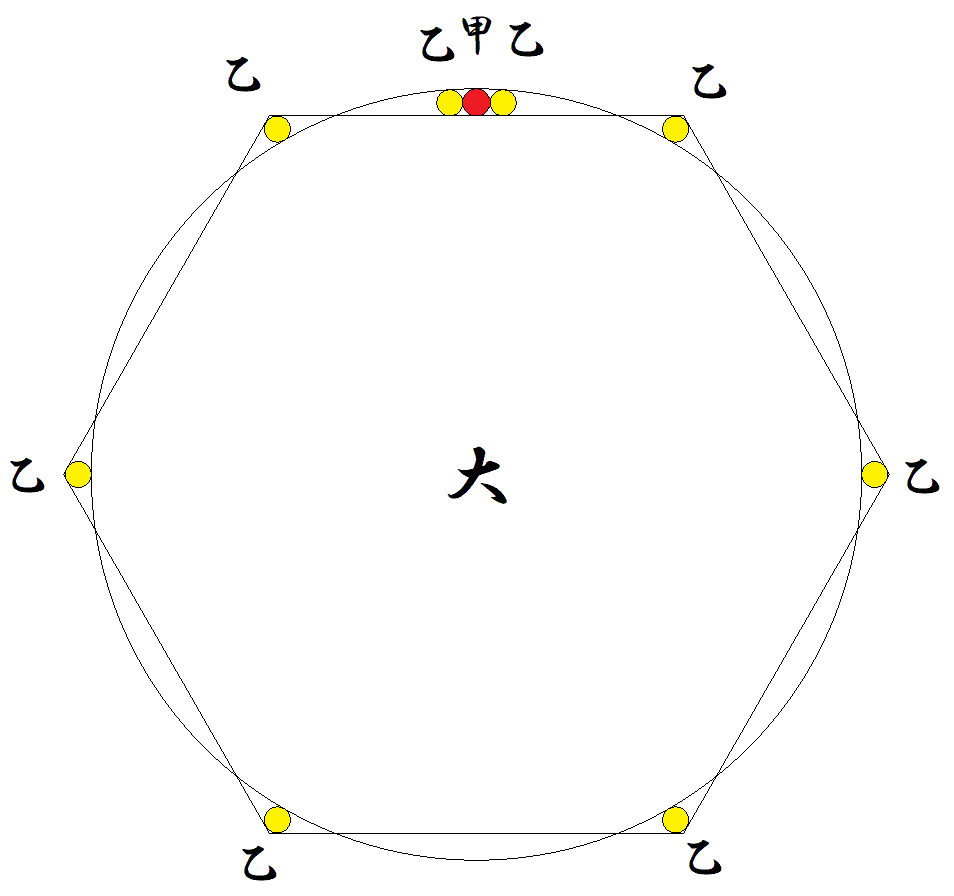









  32. 1辺の長さが1である正五角形の内部に
    辺を共有する正方形2個と正三角形1個
    を図のように配置し，正方形の辺に接し，
    正三角形の頂点を通る円の半径を求めよ。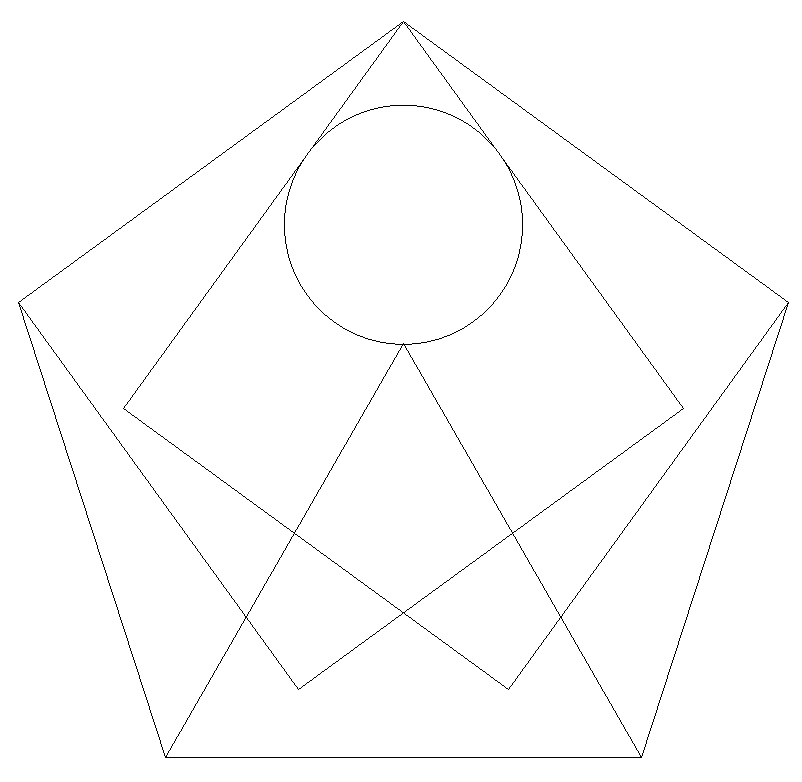



  33. 半径1の大円の1つの直径上に中線をもつ2個
    の正三角形が，図のように配置されている。
    さらに，正三角形の頂点を通り，辺に接し，
    大円に内接する2個の小円を入れる。
    このとき，小円の半径を求めよ。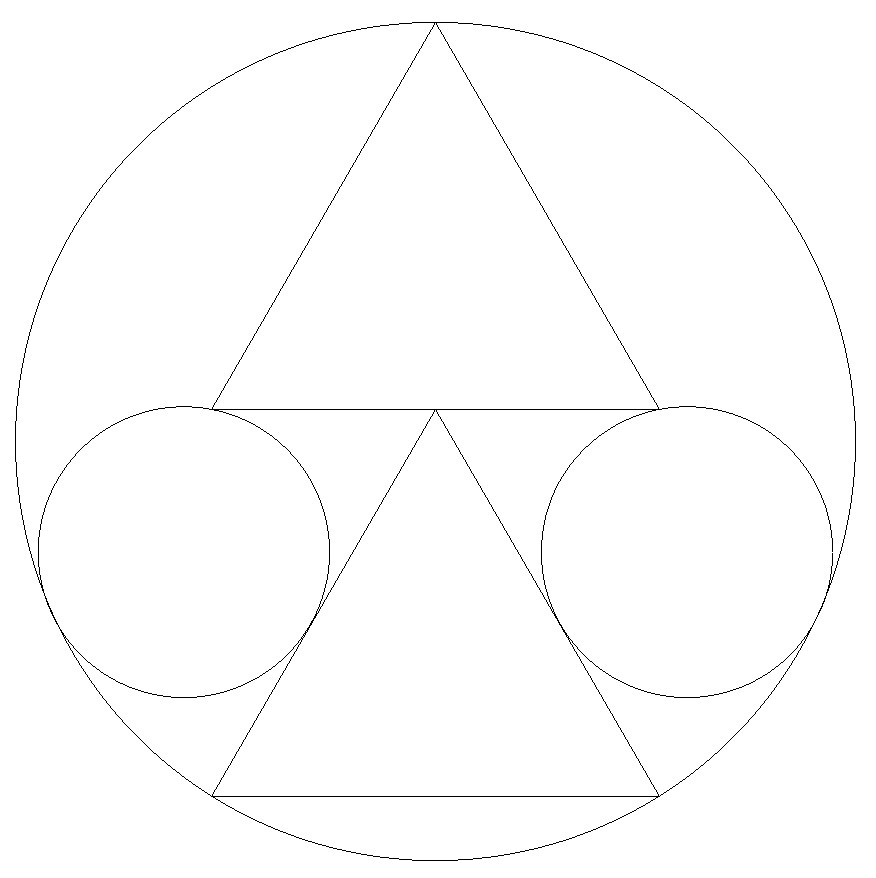



  34. △ABCについて，∠ABC＝∠ACB＝θ，
    BCの中点をOとする。
    長軸がBC上，短軸が直線AO上にある
    楕円の長軸を2a，短軸を2bとするとき，
    AO，BOをそれぞれ求めよ。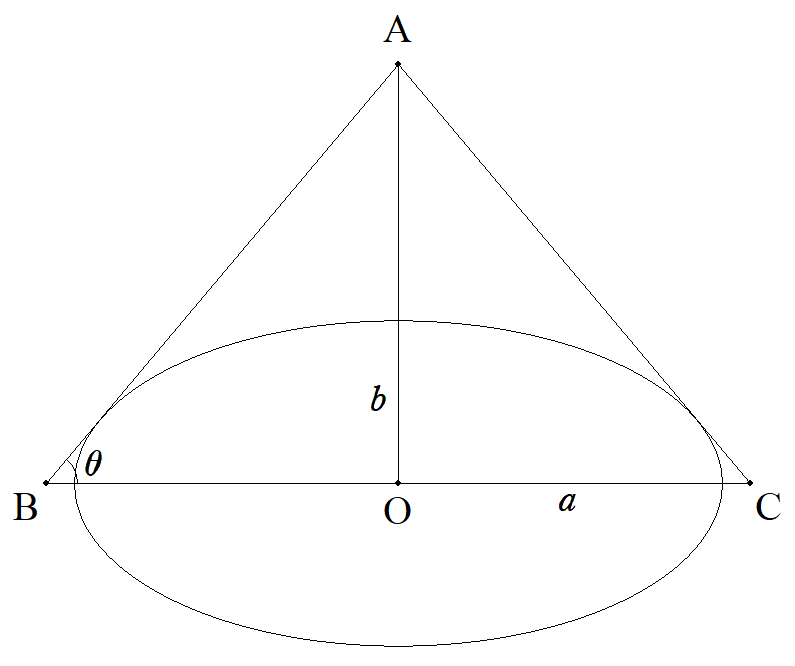



  35. 図のように，正方形内に2個の正三角形，2個の
    等楕円，1個の円を入れる。
    楕円の長軸は2aで，辺に平行である。
    このとき，正三角形が重なってできるひし形に
    内接する円の半径を求めよ。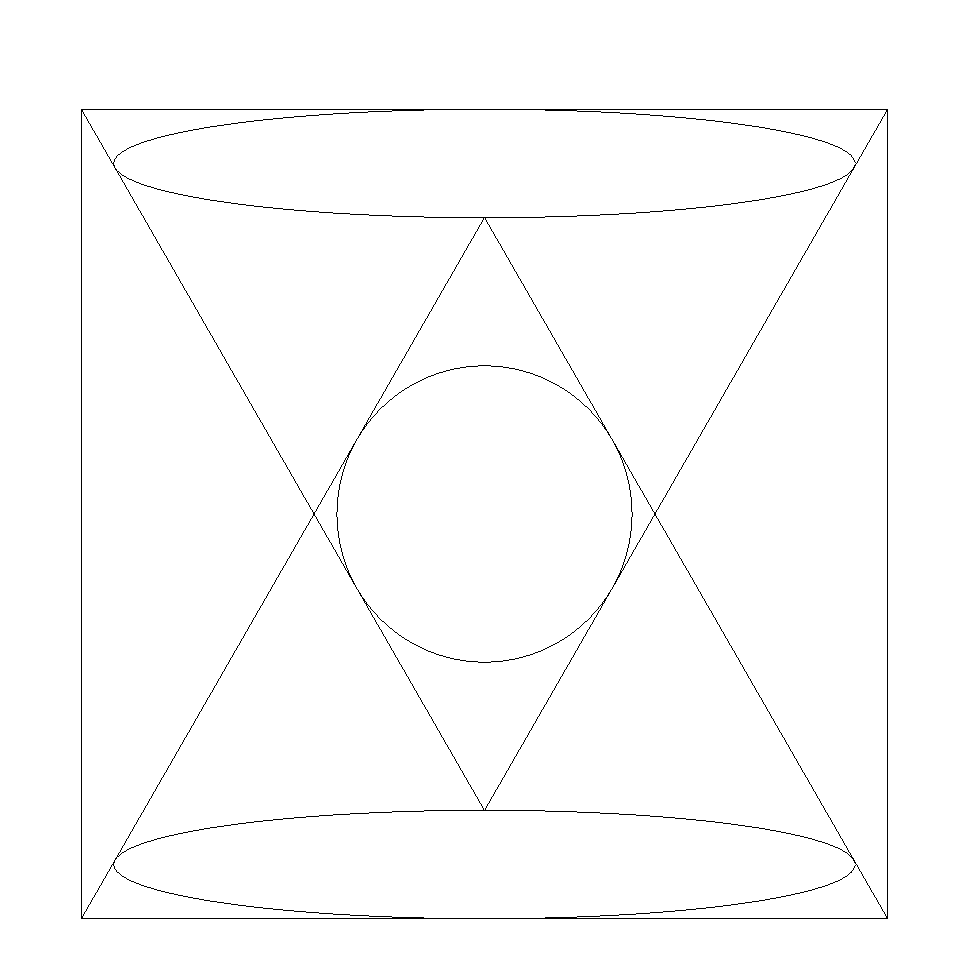



  36. 正三角形ABC内に長軸2a，短軸2bの楕円
    O1が内接している。BCの中点をDとする。
    楕円O2は，楕円O1と合同で，楕円O2の
    長軸と楕円O1の短軸は直線AD上にある。
    また，楕円O2の長軸の端で内接する円O3
    は最大円で，頂点Aを通る。
    このとき，a/b=tとおくとき，tの満たす
    方程式を一つ求めよ。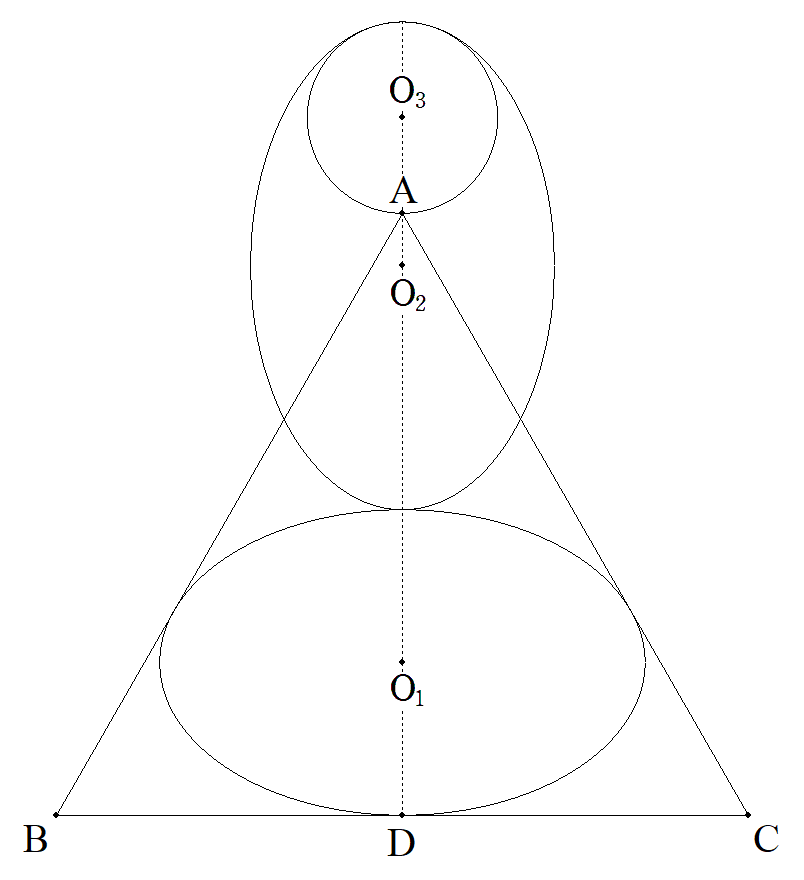









  39. 四角形ABCDはOを中心とする円に内接し，
    AB＝a，BC＝b，CD＝c．DA＝dとし，
    四角形ABCDの面積をSとする。
    四角形の対角線の交点をEとし，△EBC，
    △ECDの外心をそれぞれP，Qとする。
    COを2:1に外分する点をA´，
    CPを2:1に外分する点をB´，
    CQを2:1に外分する点をD´とする。
    このとき，次の問いに答えよ。
    (1)　四角形A´B´CD´は円に内接することを示せ。
    (2)　四角形A´B´CD´の面積S´を求めよ。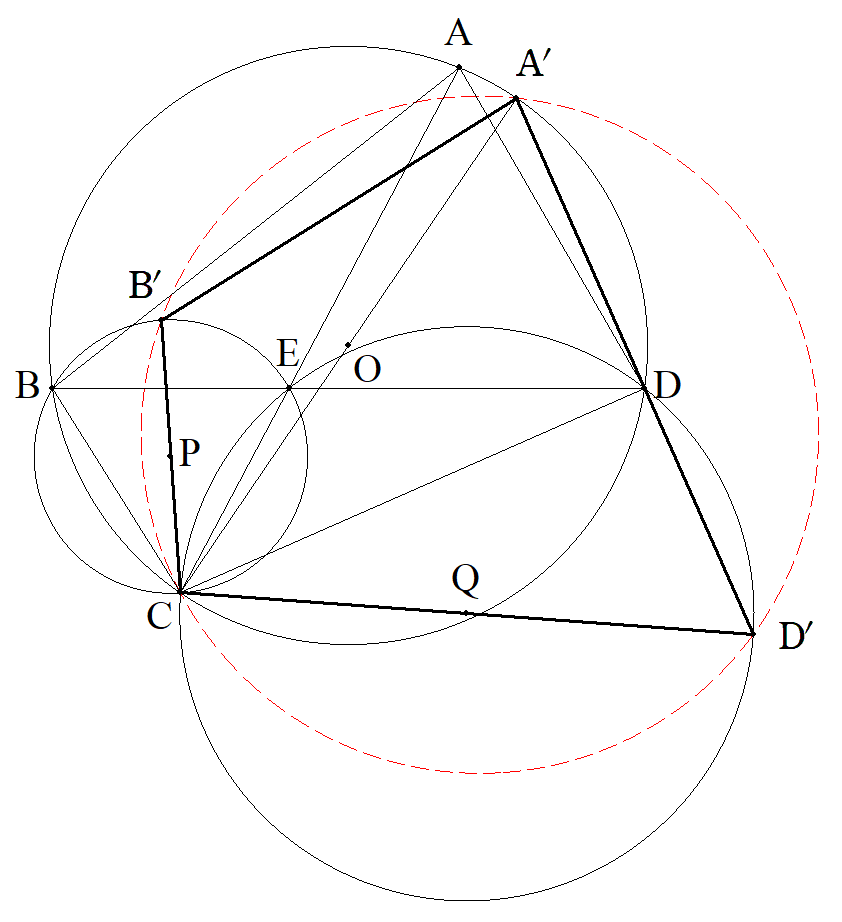



  40. 直角三角形内に相似な甲，乙楕円が
    内接している。
    甲の短軸と乙の長軸は中線上にある。
    乙の長軸の端に接する円は最大円で，
    甲に接している。
    このとき，長軸÷短軸の値tの満たす
    方程式を1つ求めよ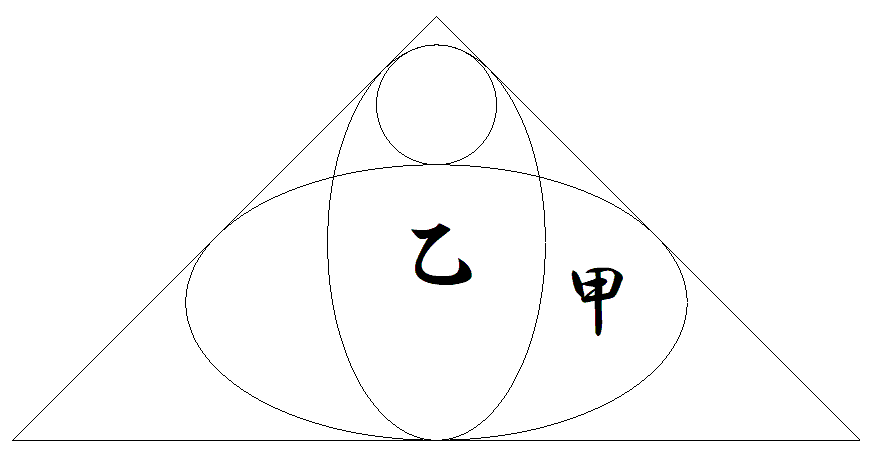



  41. 1辺の長さが1である正三角形の3個の頂点から
    等しい長さの斜線を2本ずつ引くと，2種類の
    三角形が3個ずつ，四角形と五角形が3個ずつ，
    六角形が1個できる。
    三角形の内接円がすべて等円になるとき，図の
    aの値を解にもつ方程式を1つ求めよ。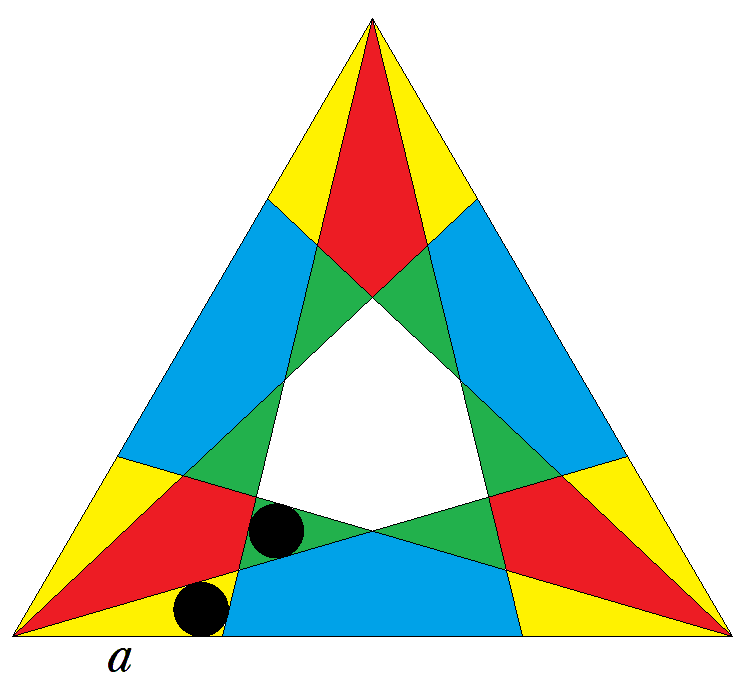



  42. 図のように，正三角形内に甲円，乙円3個，楕円が配置されている。
    楕円の長軸は底辺に平行で，正三角形とその内接円甲に接している。
    楕円の長軸の端で接する乙円は最大円で，楕円に外接する乙円は正
    三角形に接している。
    このとき，
    (1)　長軸÷短軸の値をtとおくとき，tを解とする方程式を1つ求
    　　めよ。
    (2)　短軸が2のとき，正三角形の1辺を求めよ。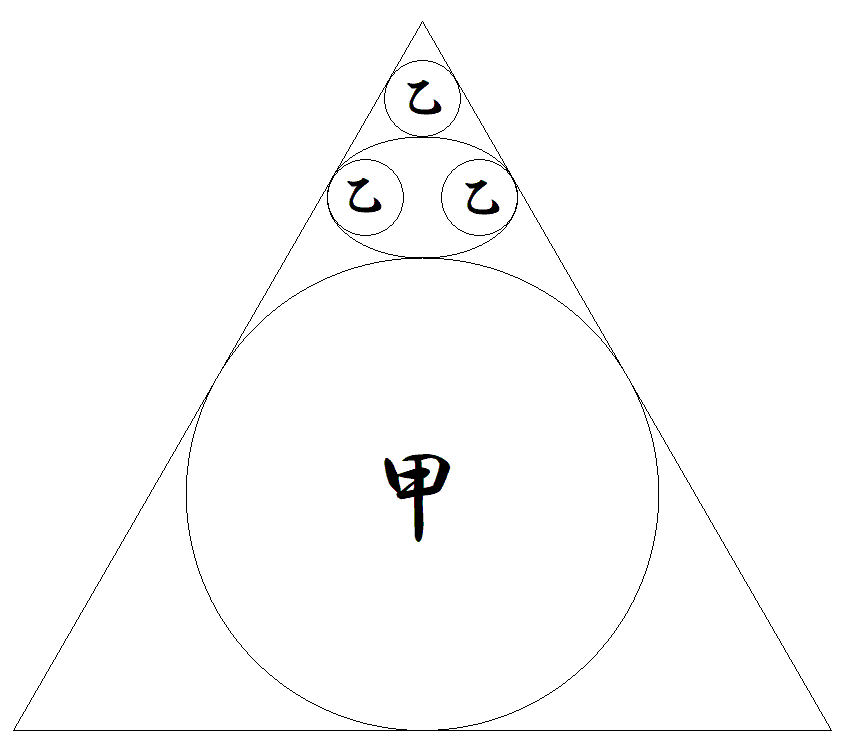



  43. 半径1の円周上に直径の両端の点があり，
    互いに外接する5個の合同な半円の半径を
    求めよ。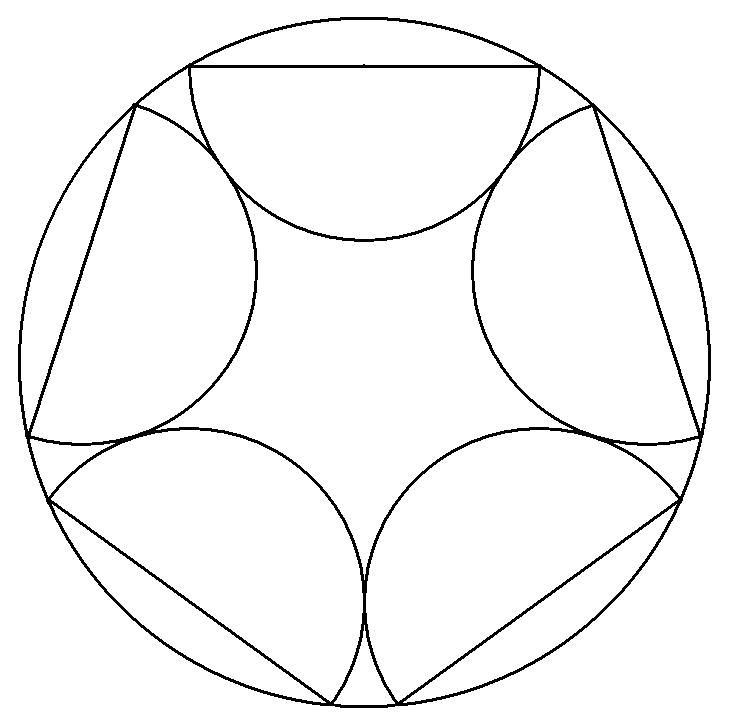



  44. BC=CA=1，∠BCA＝90°である△ABCのCA上に点Dを
    ∠DBC＝30°となるようにとり，△DBCの内接円をO1(r)
    とする。円O2は，円O1と等円で，AB，BCに接している。
    このとき，O1O2を求めよ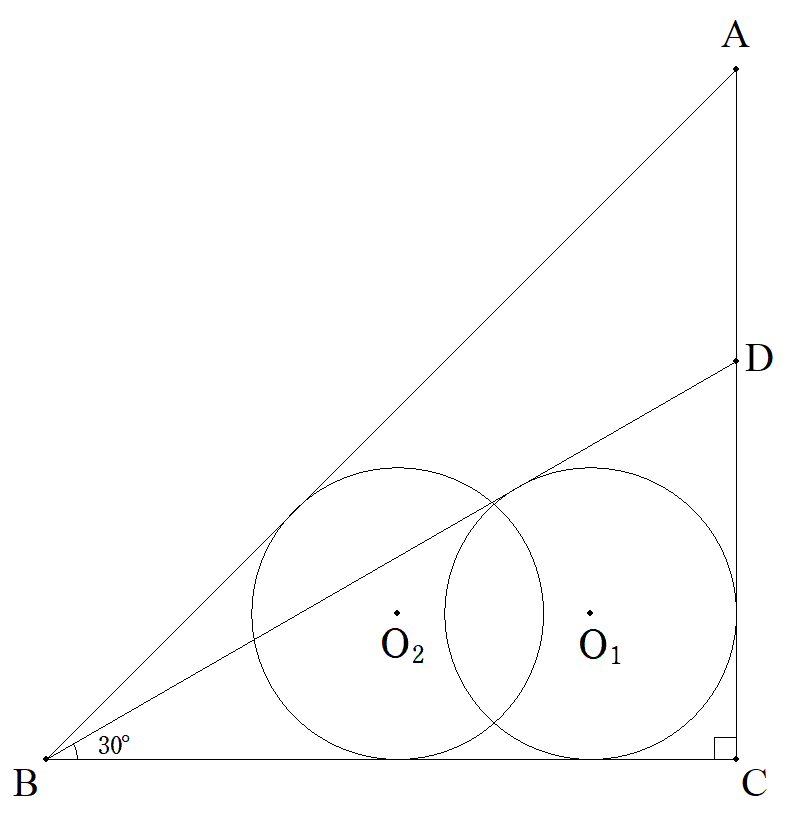



  45. ∠ABC＝45°，BC＝1，∠BCA＝90°である△ABCについて，
    ∠Bの3等分線とCAとの交点をCに近い方からD，Eとする。
    △DBCの内接円をO1(r)，円O2は円O1と等円で，EB，BC
    に接している。円O3は円O1と等円で，AB，BCに接している。
    このとき，
    (1)　O1O2を求めよ。
    (2)　O2O3を求めよ。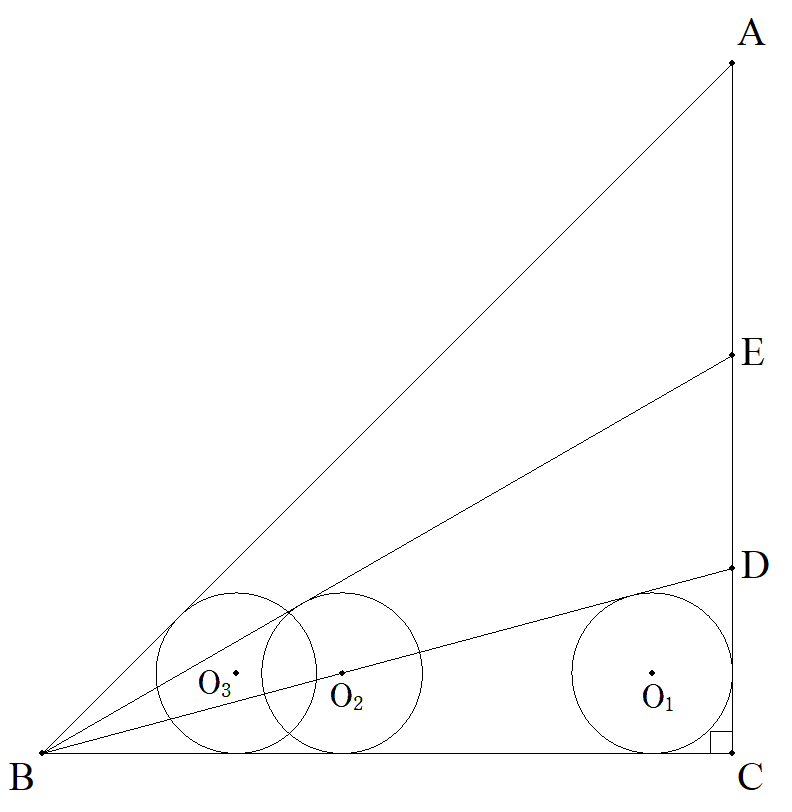



  46. ∠ABC＝45°，BC＝1，∠BCA＝90°である△ABCについて，
    ∠Bの3等分線とCAとの交点をCに近い方からD，Eとする。
    △DBCの内接円をO1，円O2は円O1に外接し，EB，BCに
    接している。
    円O3は円O1に外接し，AB，BCに接している。
    このとき，3円O1，O2，O3の半径をそれぞれ求めよ。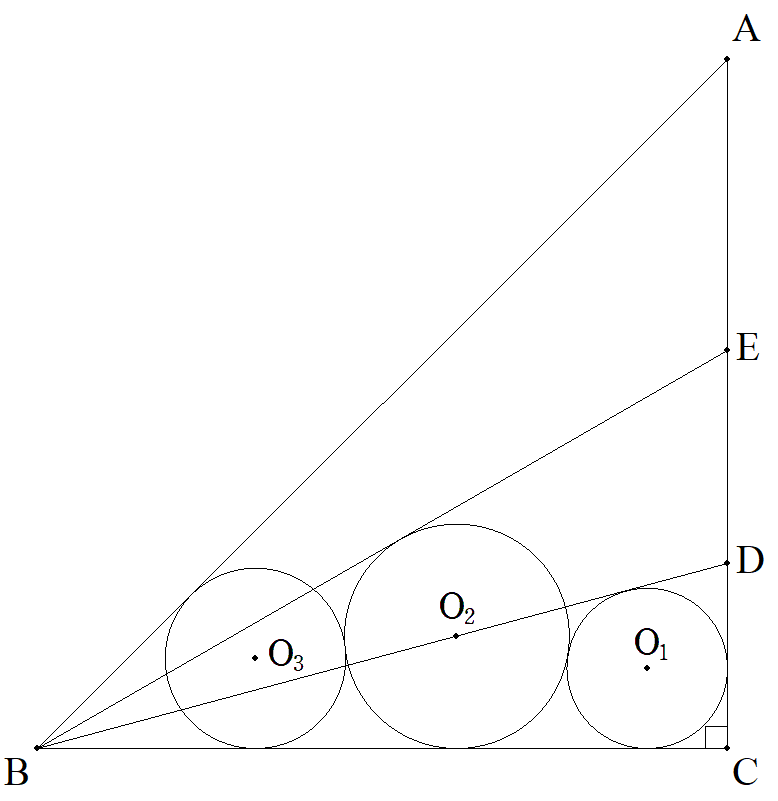



  47. 縦の長さが4である長方形内に3個の等楕円は互いに
    外接し，軸が辺に平行になるように内接している。
    このとき，長方形の横の長さを求めよ。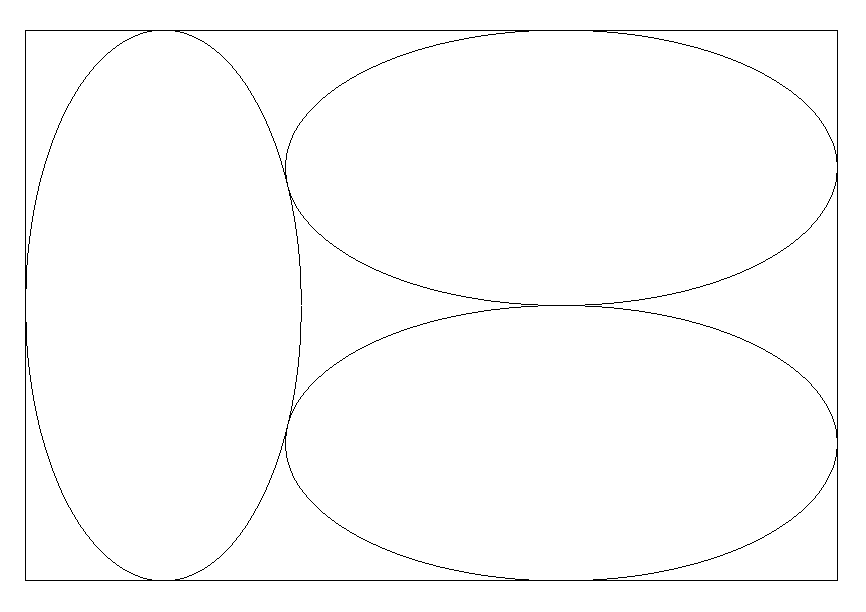



  48. 正五角形の各辺に長軸をもつ5個の楕円同士が互いに
    外接するように配置されている。
    長軸2a，短軸2bのとき，正五角形の1辺を求めよ。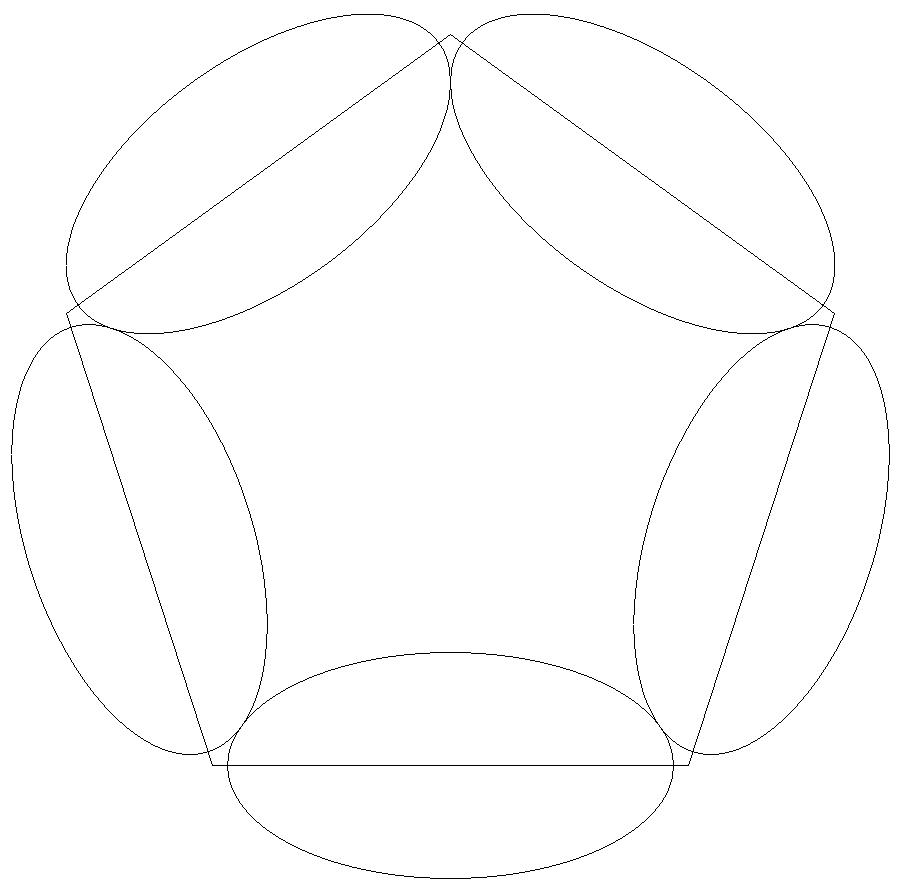



  49. 縦の長さが4である長方形内に軸が辺に平行である
    4個の楕円甲が図のように内接している。
    このとき，長方形の横の長さを求めよ。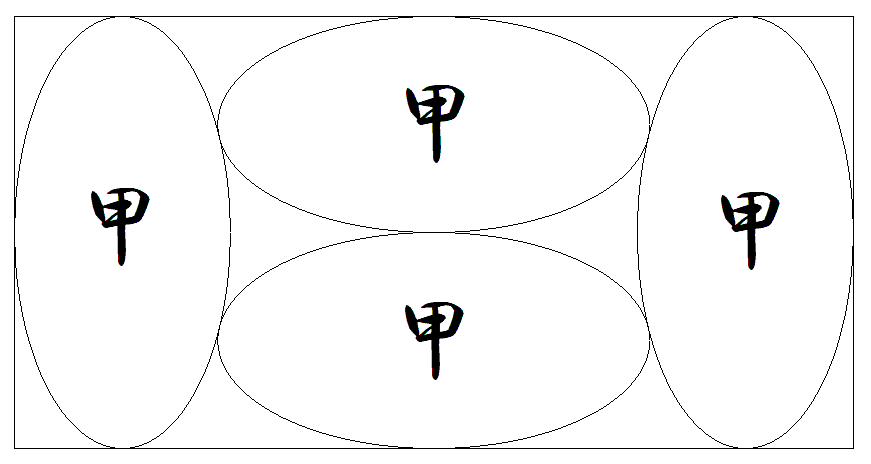



  50. BC=61，CA=AB=32である△ABCの
    ∠Aの5等分線とBCとの交点をBに近い
    方からD，E，F，Gとするとき，BD，
    DE，EFを求めよ。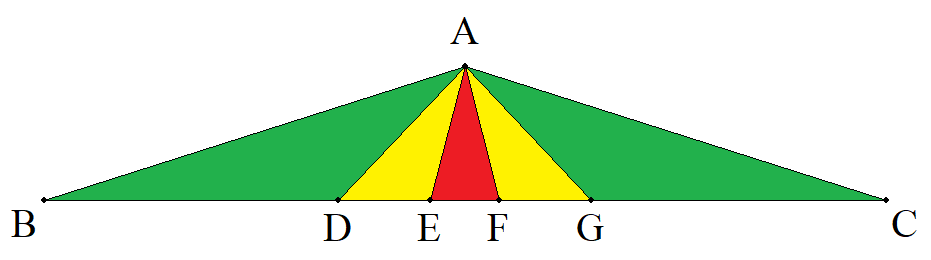