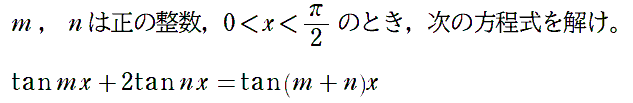■趣味の数学問題集・Ｂ問題

---

351. 
     

     BC＝25199，CA＝AB＝16384である△ABCの ∠Aの7等分線とBCとの交点をBに近い方から D，E，F，G，H,Iとするとき，BD，DE，EF， FGをそれぞれ求めよ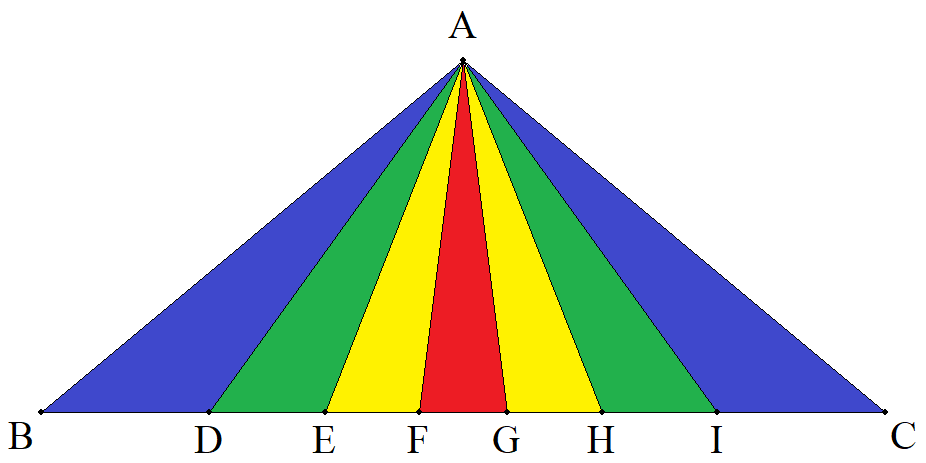

     
     
     
352. 
     

     半径Rの円内に3本の直径を引き，その間に 図のように甲乙丙円を2個ずつ入れる。 甲乙丙円の半径をそれぞれr1，r2，r3とする とき，r3をR，r1，r2を用いて表せ。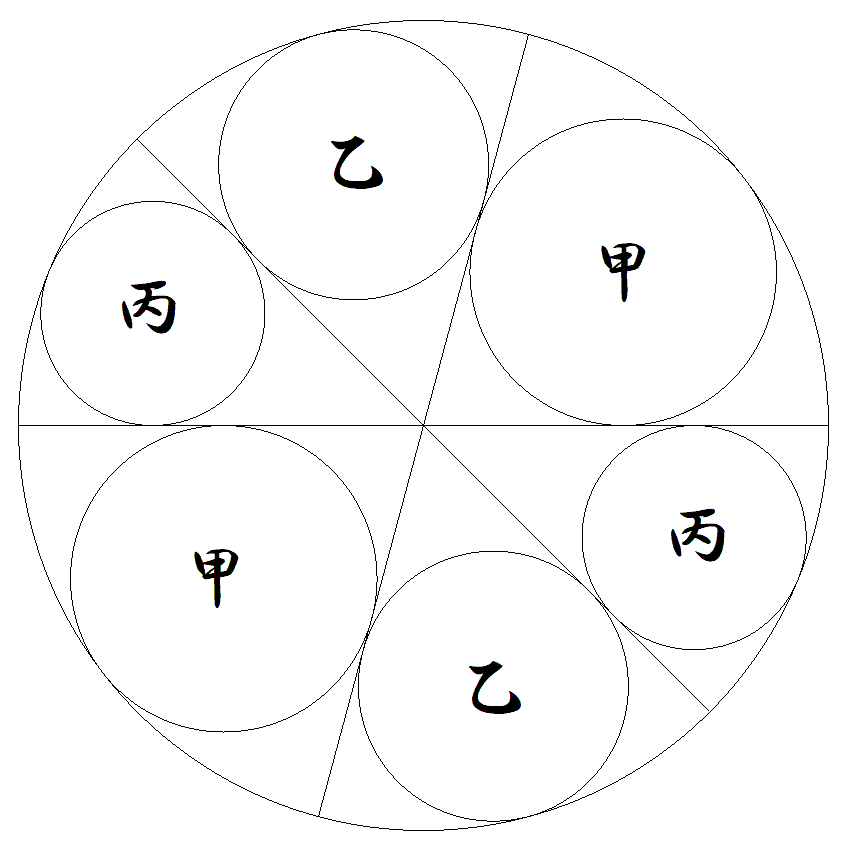

     
     
     
353. 
     

     楕円内に正三角形甲1個と乙2個が 図のように配置されている。 甲の頂点は短軸の端にあり， その対辺は長軸に平行である。 丙の頂点は長軸の端にあり， その対辺は短軸に平行である。 このとき，（乙一辺）÷（甲一辺） の値を求めよ。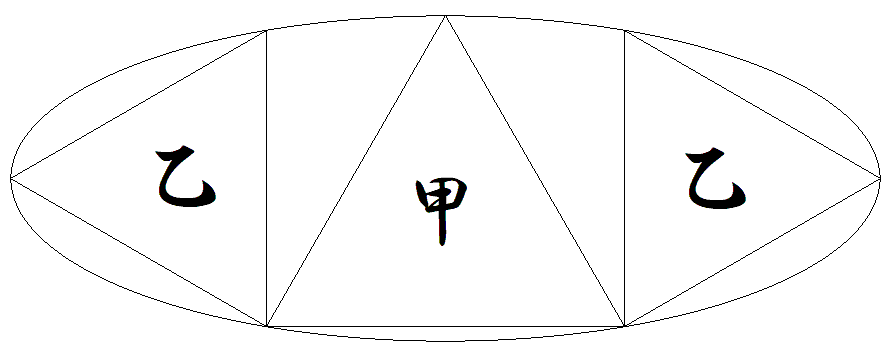

     
     
     
354. 
     

     短軸が2である楕円内に正三角形2個と 直角二等辺三角形2個が入っている。 三角形の1辺は短軸に平行である。 正三角形と直角二等辺三角形の面積が 等しいとき長軸を求めよ。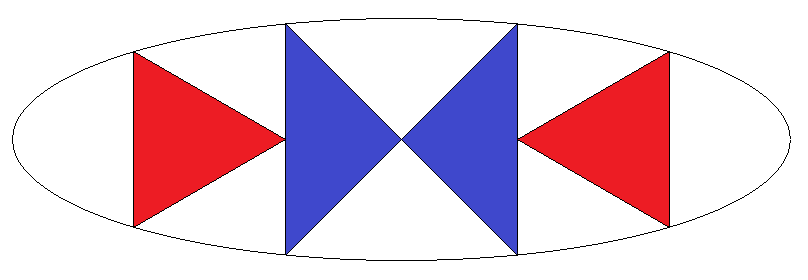

     
     
     
355. 
     

     長軸2a，短軸2bの楕円と半径rの円が外接し， 楕円の長軸に平行な共通接線をもち，接点間の 距離がcのとき，a，b，c，rの関係式を求めよ。 ただし，a＞b，r≠bとする。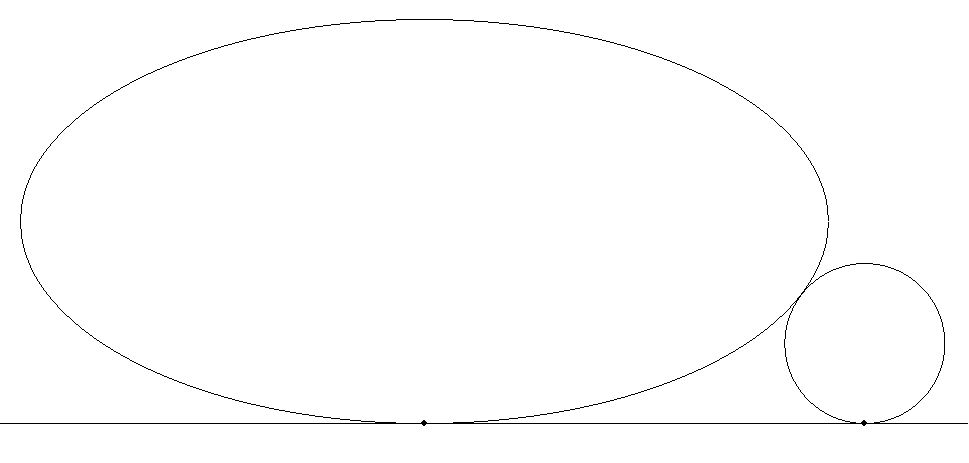

     
     
     
356. 
     

     長方形に対角線を引き，その内部に， 図のように，甲乙円2個ずつ，丙円 6個を入れる。長方形の縦を1とした とき，横aの値を解にもつ整数を係数 とする方程式を1つ求めよ。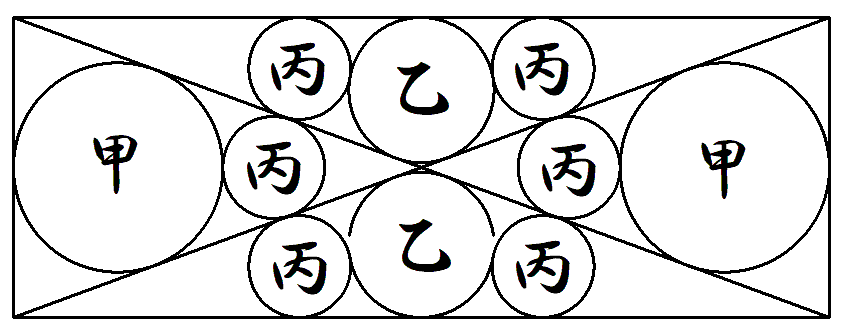

     
     
     
357. 
     

     △ABCの外側に正方形ADEB，CFGAをつくり，EF の中点をMとする。 さらに，点H，Kを四角形CMBH，DMGKが正方形 になるようにとる。 このとき，次を示せ。 (1)　AはHKの中点 (2)　EF⊥HK (3)　EF＝HK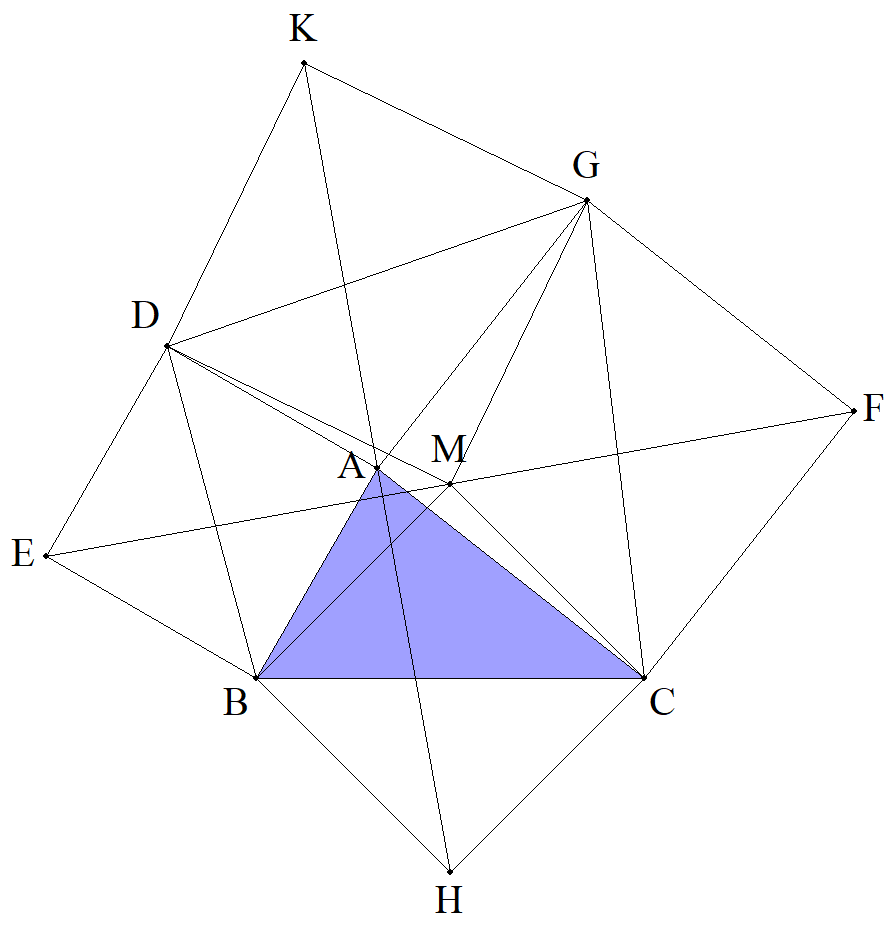

     
     
     
358. 
     

     互いに接する3個の相等しい楕円がある。これ等の楕円内に12個の相等しい円 をつくる。これらの2円は互いに外接して2つの楕円の接点で外接している。 楕円の長軸2a，短軸2bを用いて円の半径を求めよ。

     
     
     
359. 
     

     図のように楕円内に甲円1個，乙円2個，丙円2個が入っている。 乙円は長軸の端で接する最大円である。 このとき，長軸÷短軸の値tを解にもつ整係数の方程式を1つ 求めよ。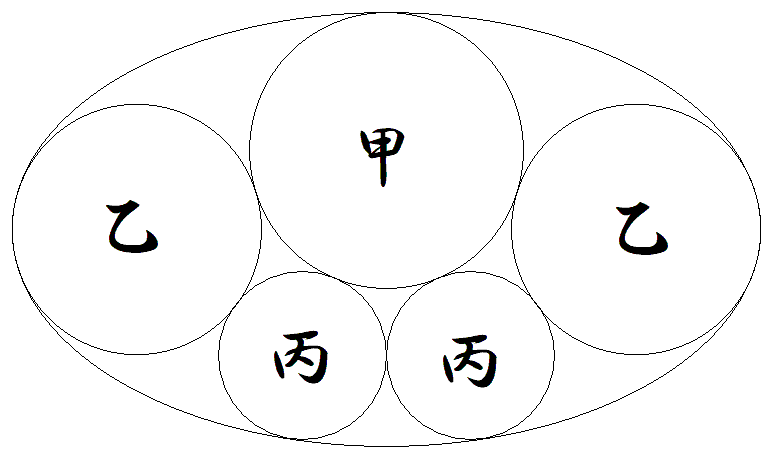

     
     
     
360. 
     

     長軸2a，短軸2bの楕円内に軸の端で接する 赤円4個と青二等辺三角形2個が入っている。 ただし，長軸の端で接する円は最大円である。 このとき，長軸÷短軸の値tを解にもつ方程式 を1つ求めよ。

     
     
     
361. 
     

     長軸2a，短軸2bの楕円内に赤円6個と青二等辺 三角形2個が入っている。 ただし，長軸の端で接する赤円は最大円である。 このとき，長軸÷短軸の値tを解にもつ方程式 を1つ求めよ。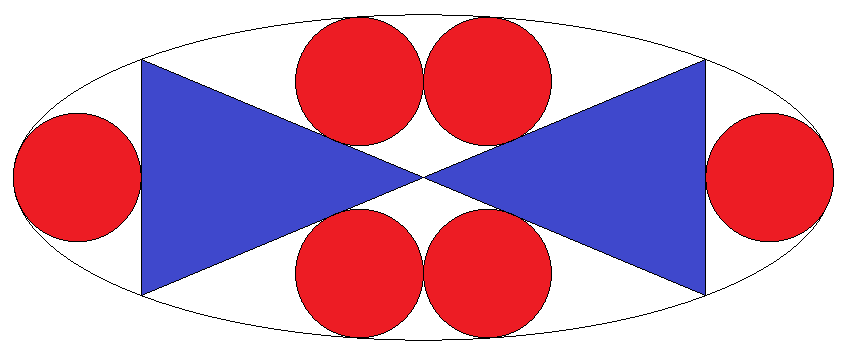

     
     
     
362. 
     

     半径1の半円と甲円3個と乙円4個が 図のように配置されている。 乙円の半径を求めよ。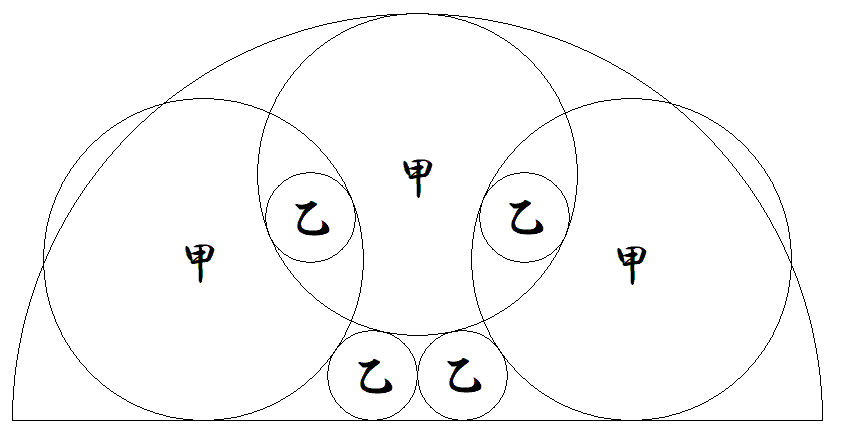

     
     
     
363. 
     

     1辺1の正七角形14個が図のように辺を共有して 環状に連結されている。このとき，囲まれた部分 （黄部）の面積Sを求めよ。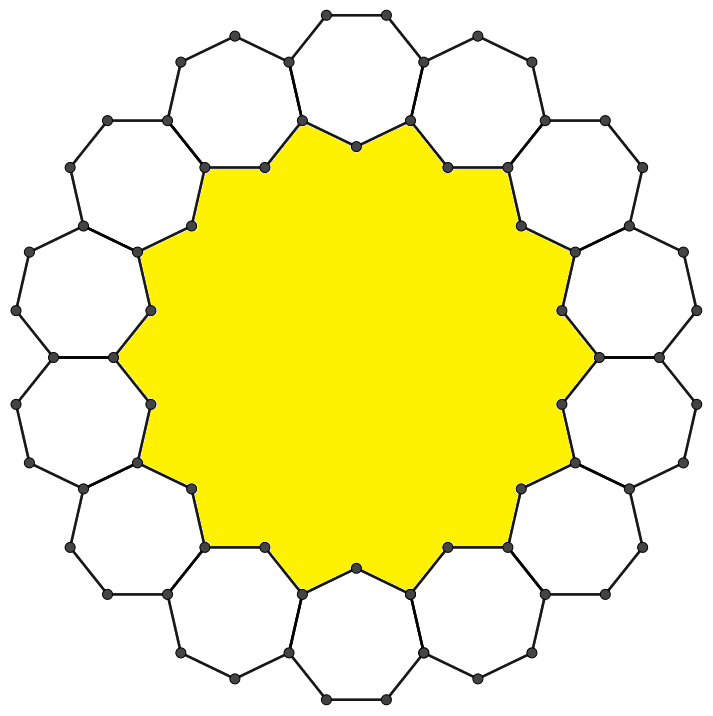

     
     
     
364. 
     

     直角三角形の中に1辺の長さが1の 正五角形が入っている。 直角三角形の底辺の長さを求めよ。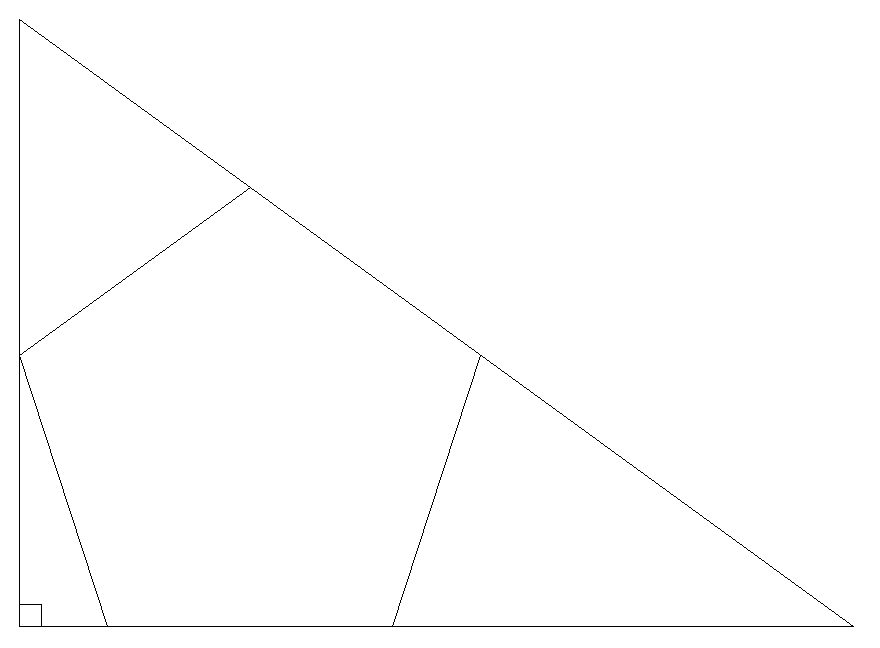

     
     
     
365. 
     

     直角三角形の中に1辺の長さが1の 正七角形が入っている。 直角三角形の底辺の長さを求めよ。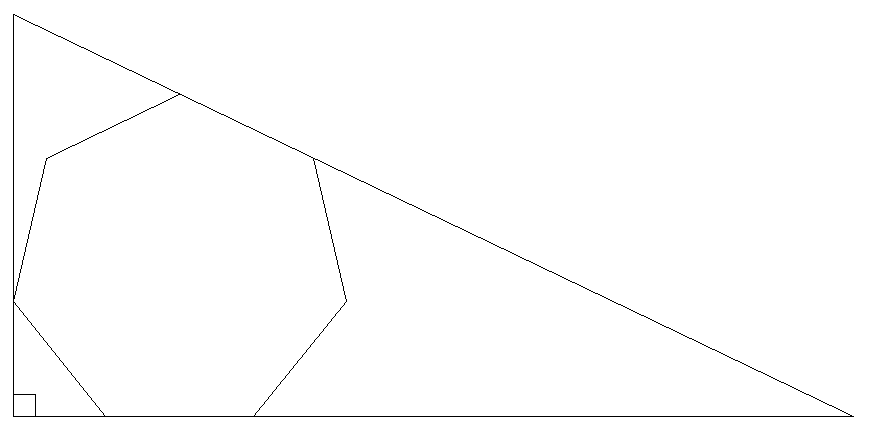

     
     
     
366. 
     

     直角三角形の中に1辺の長さが1の 正九角形が入っている。 直角三角形の底辺の長さを求めよ。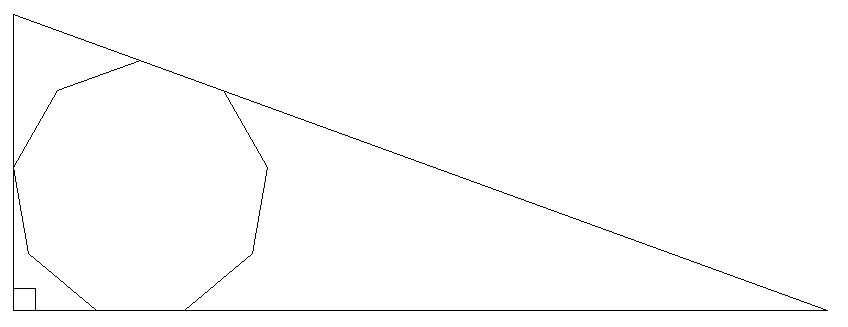

     
     
     
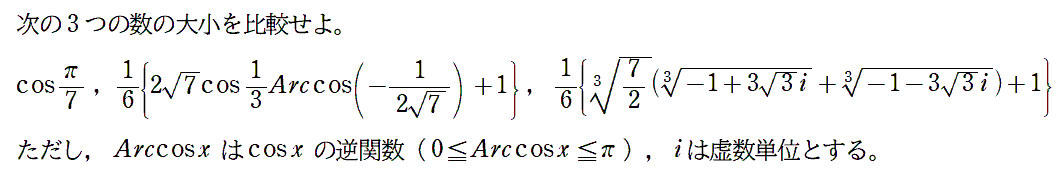
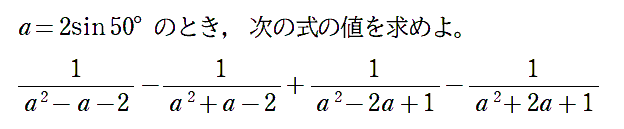
367. 
     
     
     
368. 
     
     
     
369. 
     
     
     
370. 
     
     
     
371. 
     

     1辺の長さが1である正方形内に，図のように 1個の楕円と6個の等円が入っている。ただし， 楕円の長軸の端で接する円は最大円である。 このとき， (1)　短軸を2bとおくとき，bの満たす整係数の 　　方程式を一つ求めよ。 (2)　短軸を求めよ。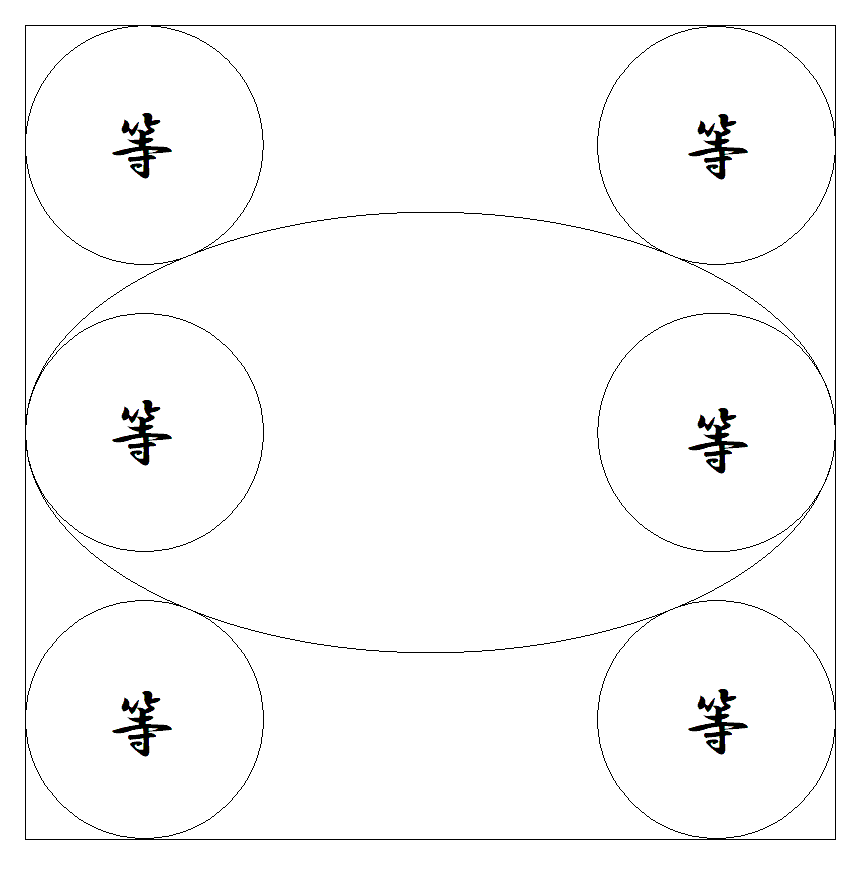

     
     
     
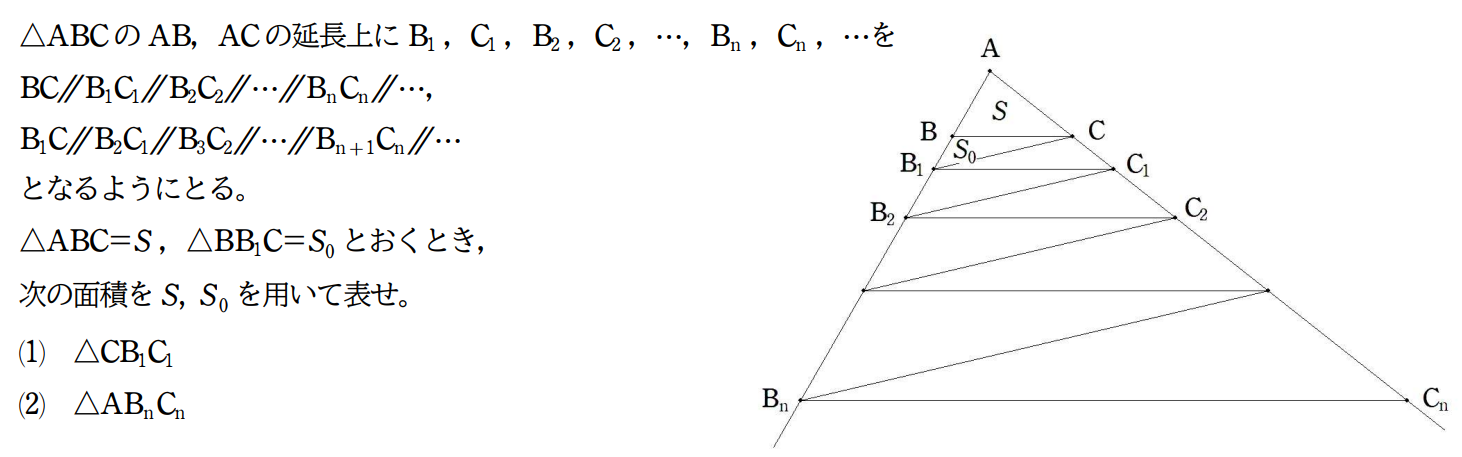
372. 
     
     
     
373. 
     

     三角形の2辺に接する3個の甲円に乙円が接している。 三角形の外接円，内接円，甲円の半径をそれぞれ R，r，r1とおくとき，乙円の半径を求めよ。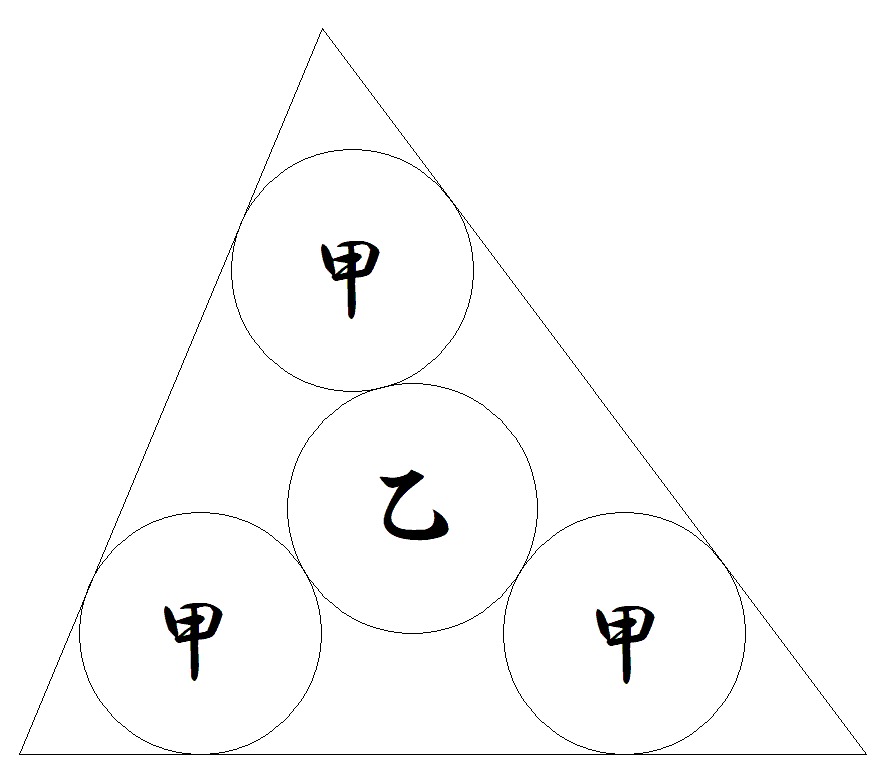

     
     
     
374. 
     

     3辺の長さが8，7，5である三角形内に， 図のように4個の等円が入っている。 等円の半径を求めよ。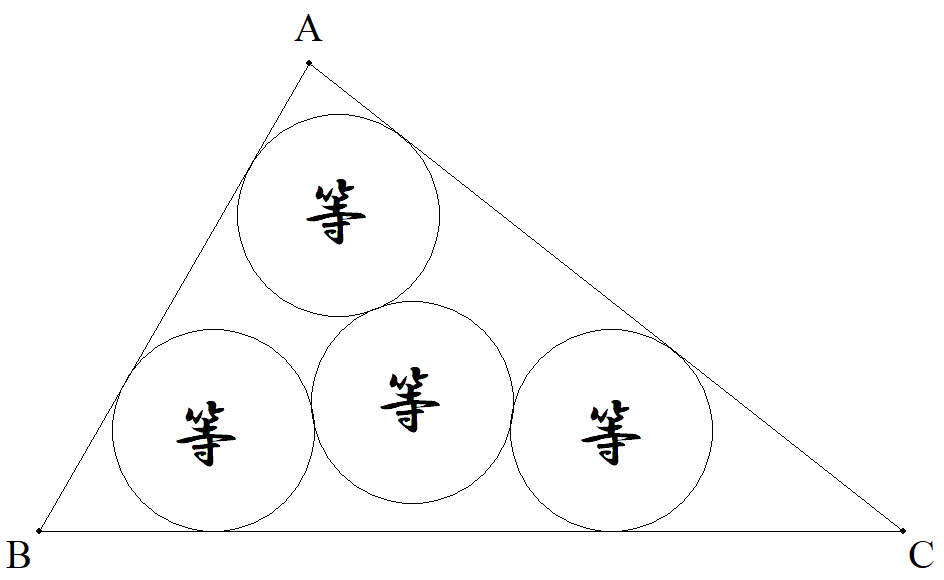

     
     
     
375. 
     

     △ABCとその外接円の間に図のように甲乙丙円を入れる。 ただし，甲乙丙円は辺の中点で接している。 三角形の外接円，内接円の半径をそれぞれR，rとおく とき，甲乙丙円に接する丁円の半径を求めよ。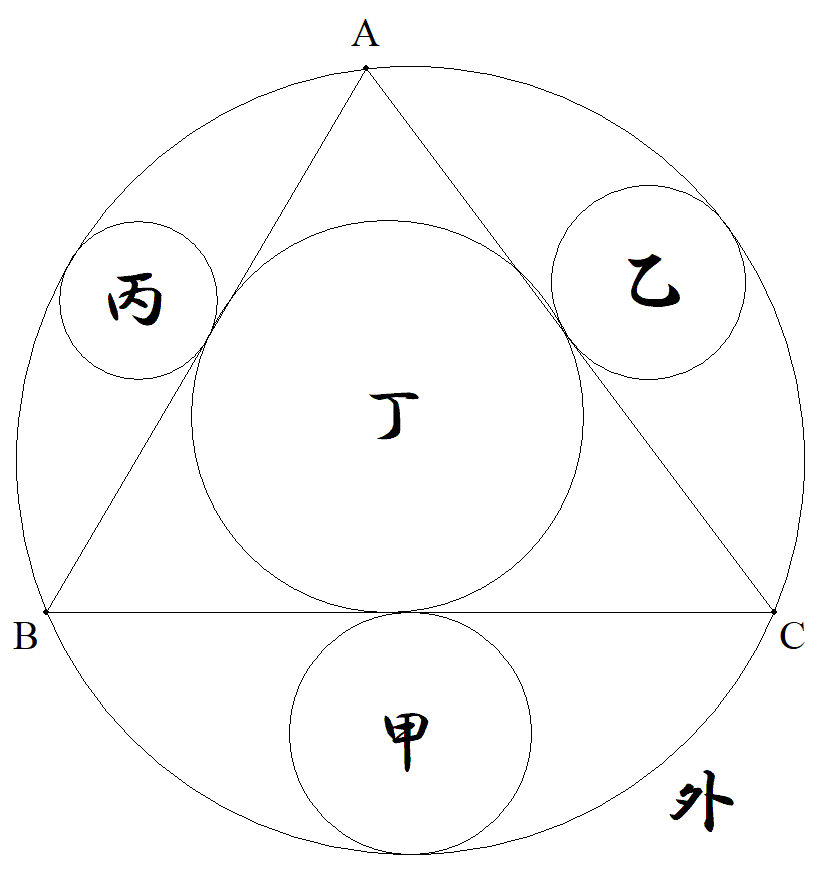

     
     
     
376. 
     

     a=15，b=14，c=13の△ABCについて， Aを中心とする半径nの円， Bを中心とする半径n＋1の円， Cを中心とする半径n＋2の円を描く。 これら3円に外接する円Pの半径を求めよ。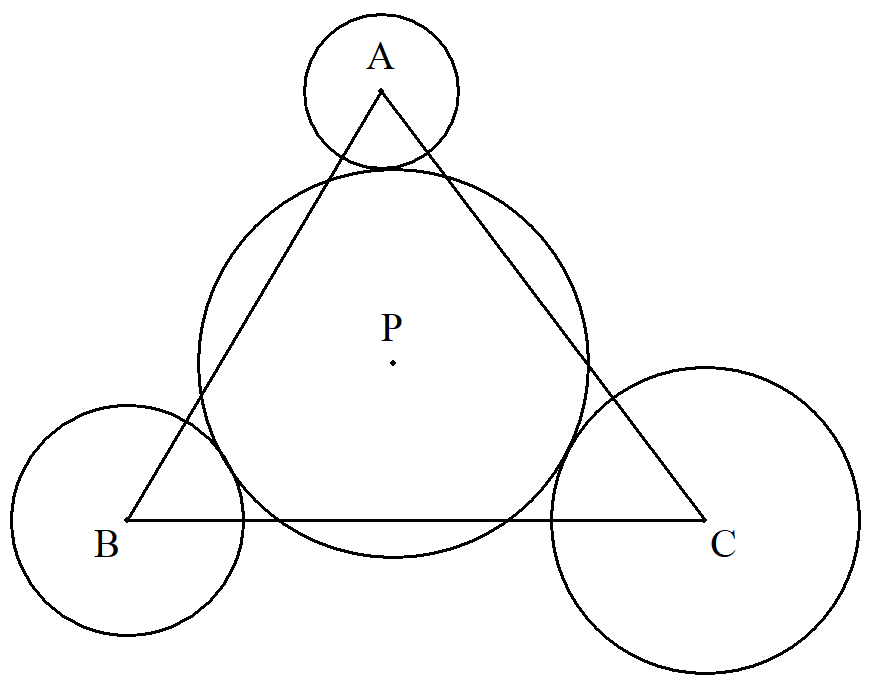

     
     
     
377. 
     面積Sの△ABCの外接円の半径がRで，BC＝aのとき，次の式の値を求めよ。
     (1)　cosA+cosBcosC
     (2)　sinA+sinBsinC
     
     
378. 
     
     
     
379. 
     
     
     
380. 
     △ABCの角の二等分線に関して中線を折り返した3直線は1点Pで交わることが知られている。
     （この交点をルモワーヌ（Lemoine）点という。）
     APとBC，BPとCA，CPとABとの交点をそれぞれD，E，Fとおく。
     (1) BD:DC，CE:EA，AF:FBを求めよ。
     (2) ∠PAB＋∠PBC＋∠PCA＝90°のとき，△ABCの形状を考察せよ。
     
     
381. 
     

     2個の半径1，中心角60°の扇形が図のように重なっている。 図のように，その中に赤緑橙青黄紫の円が入っている。 円赤緑橙青黄紫の半径をそれぞれ求めよ。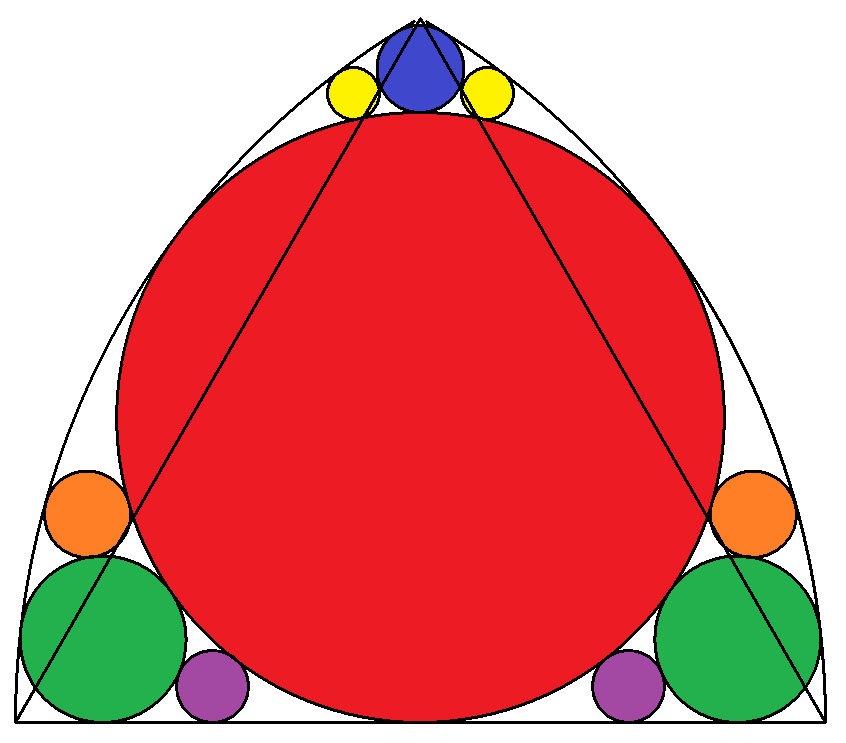

     
     
     
382. 
     

     図のように，長方形内に楕円と 6個の等円が入っている。 楕円の長軸の端に接する等円は 最大円である。 長方形の縦の長さが2のとき， 横の長さを求めよ。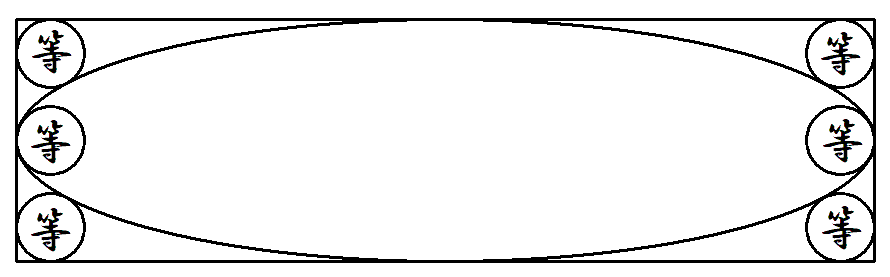

     
     
     
383. 
     ax+by+cz=2，ax²+by²+cz²=3，ax³+by³+cz³=5，ax⁴+by⁴+cz⁴=7，
     ax⁵+by⁵+cz⁵=11，ax⁶+by⁶+cz⁶=13のとき，次の問いに答えよ。
     (1)　ax⁷+by⁷+cz⁷，ax⁸+by⁸+cz⁸の値をそれぞれ求めよ。
     (2)　a，b，c，x，y，zの値を求めよ。
     (3)　axⁿ+byⁿ+czⁿの値を求めよ。
     
     
384. 
     

     次の式を簡単にせよ。

     
     
     
385. 
     

     図のように正八角形内に2個の正方形甲と1個の正方形乙が 入っている。 1個の正方形甲の面積が1のとき正方形乙の面積を求めよ。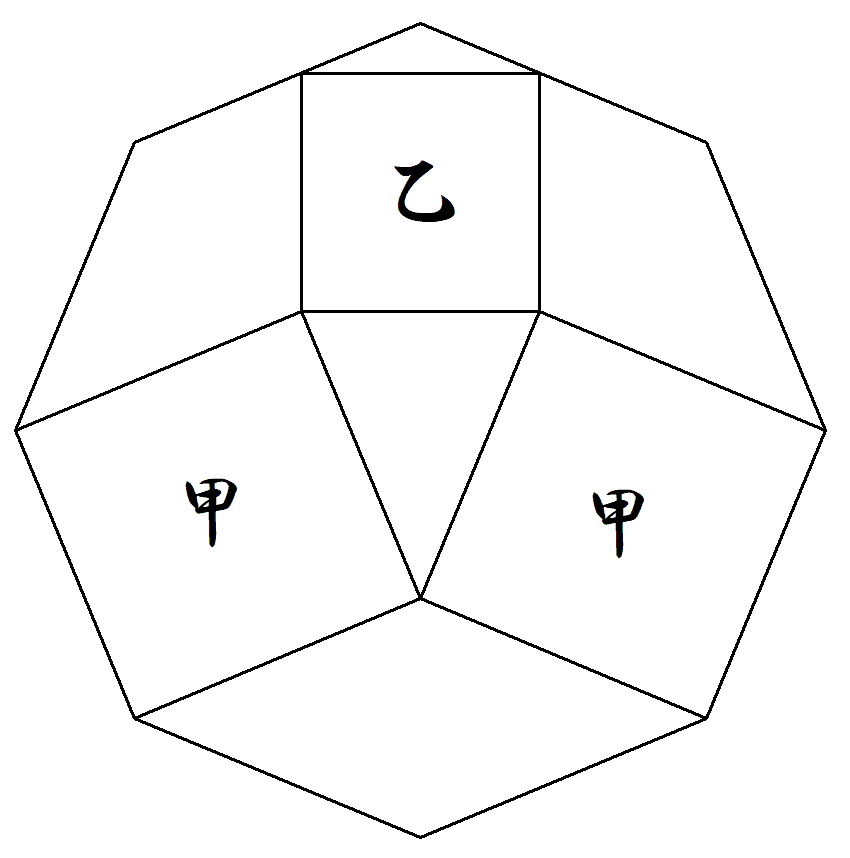

     
     
     
386. 
     

     1辺1の正六角形ABCDEFと正方形CDGHが 図のように配置されている。 EGとABの交点をIとするとき，GIを求めよ。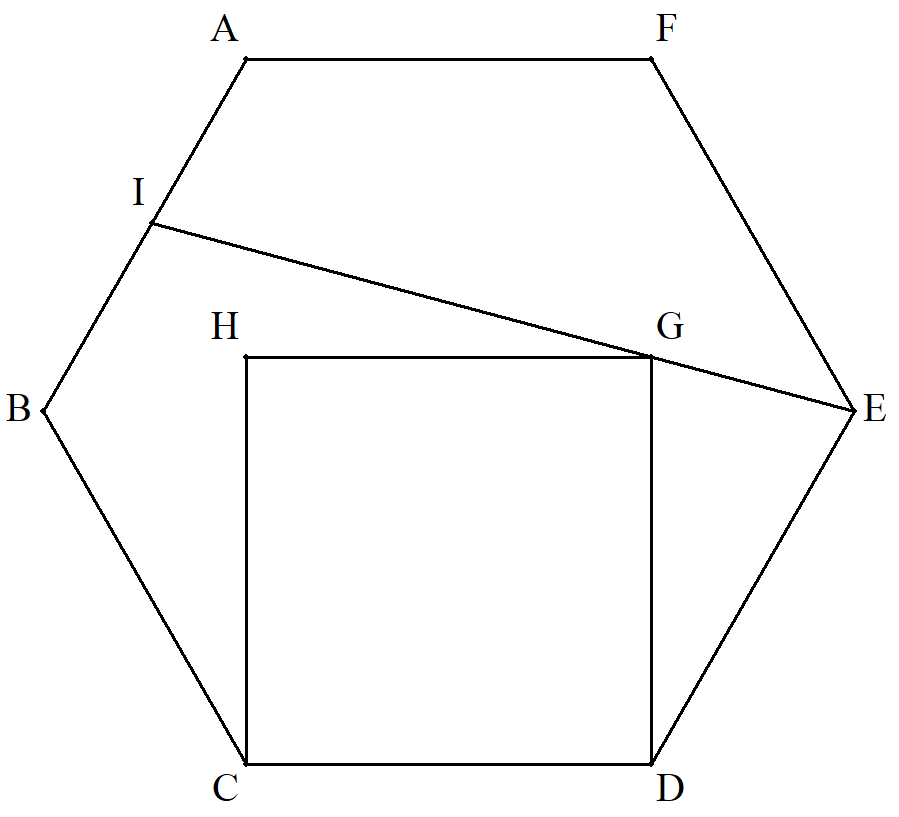

     
     
     
387. 
     

     正五角形ABCDE内に2個の正方形 BCFG，DEHIを描き，IFを1辺とす る正方形IFJKを図のように描くと， J，Kは正五角形の辺上にあることを 証明せよ。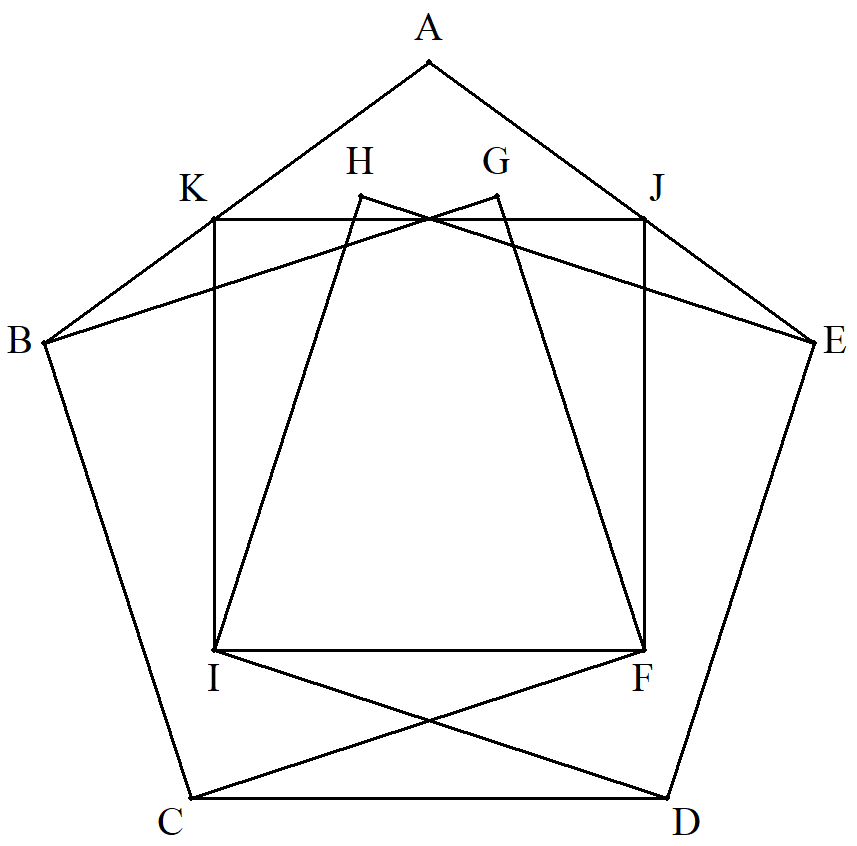

     
     
     
388. 
     

     正八角形ABCDEFGH内に2個の 正方形CDIJ，FGKIを描き，JK を1辺とする正方形JKLM を図の ように描くと，L，Mは正八角形 の辺上にあることを証明せよ。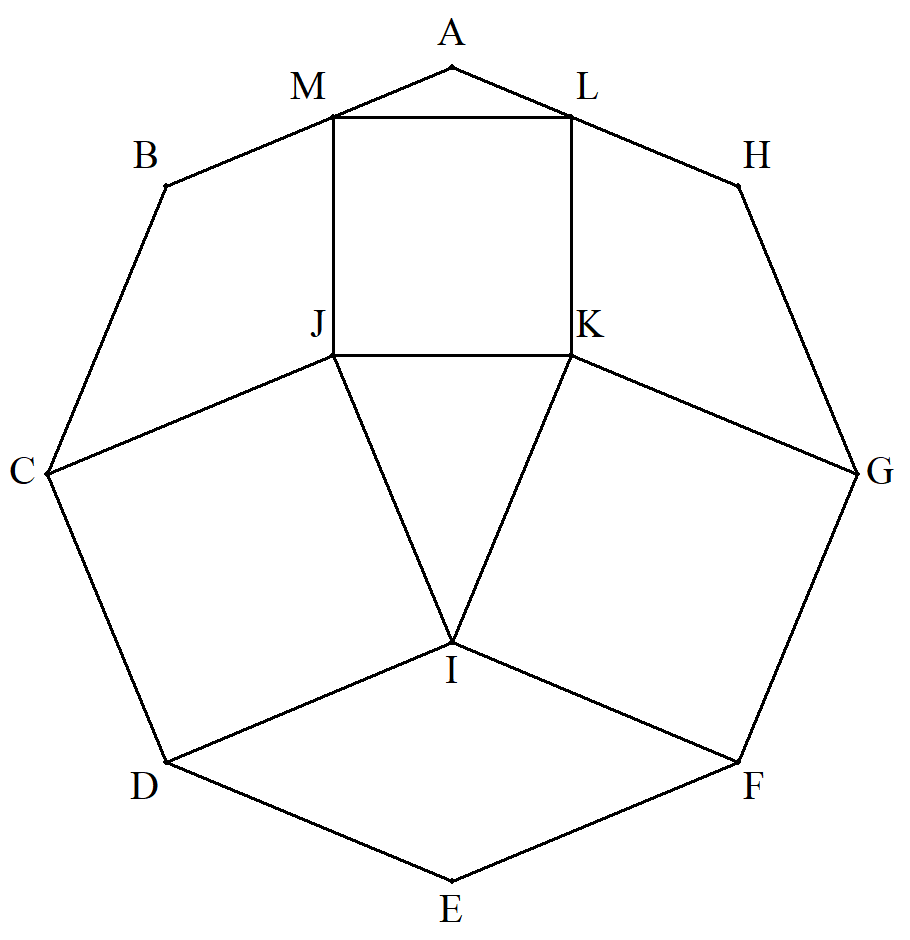

     
     
     
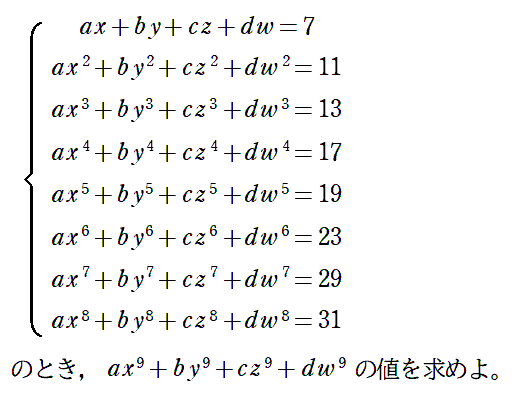
389. 
     
     
     
390. 
     

     大円内に3本の直径を引き，その隙間に 図のように甲乙丙円を2個ずつ入れる。 甲乙丙円の半径をそれぞれ10，7，2と するとき，大円の半径を求めよ。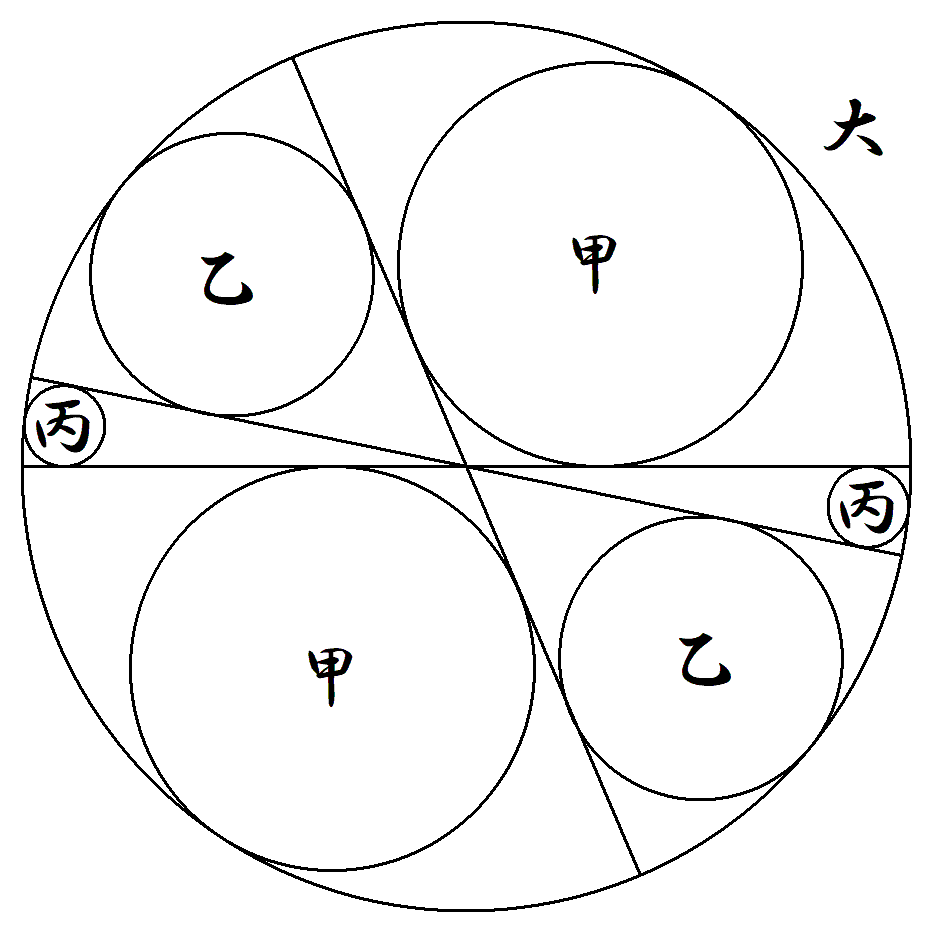

     
     
     
391. 
     

     1辺の長さがaの正五角形ABCDEに対角線を引き 星形をつくるとき，その星形の面積を求めよ。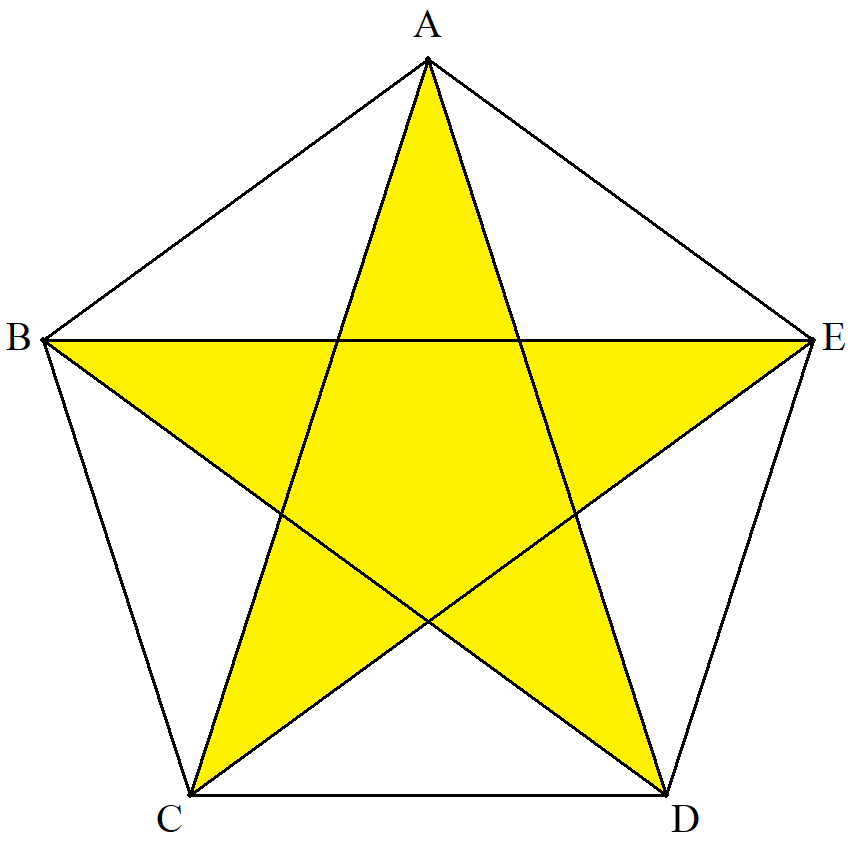

     
     
     
392. 
     
     
     
393. 
     

     正八角形ABCDEFGH内に正方形 CDIJ,FGKIを描き，JKを1辺とす る正方形JKLMを図のように描く。 正八角形の1辺の長さを1とする とき，六角形CDFGLMの面積を 求めよ。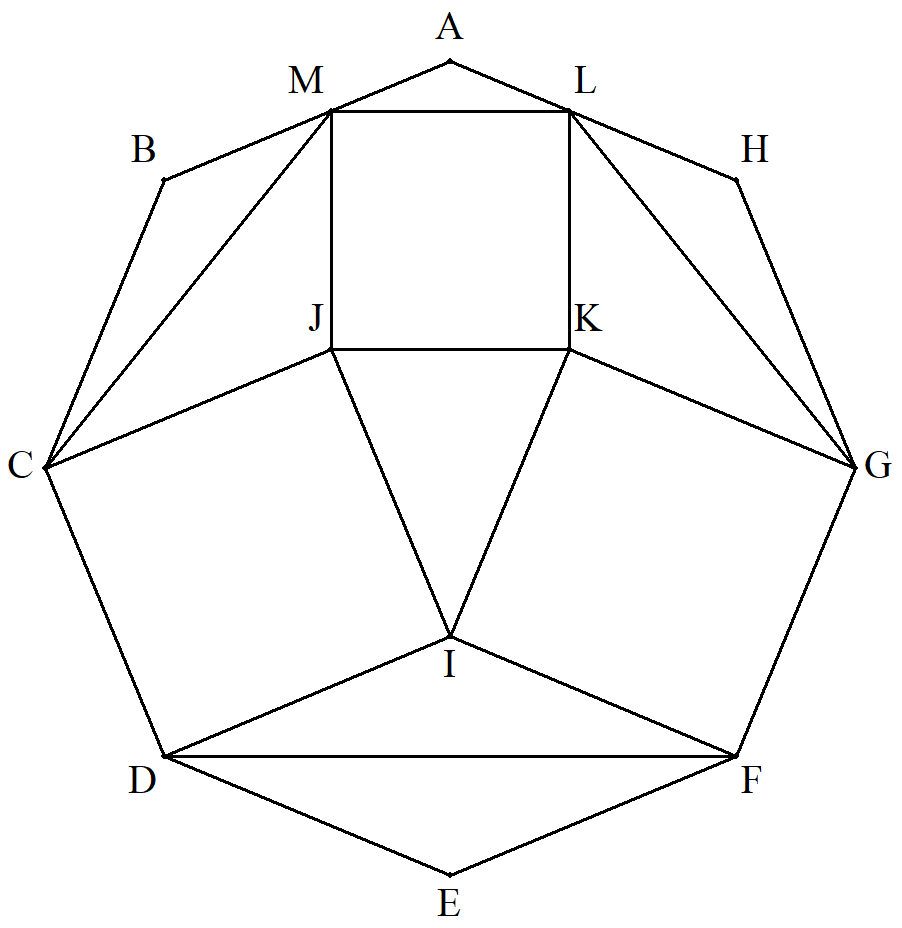

     
     
     
394. 
     

     正九角形ABCDEFGHIについて BH，CIの交点をJ，CF，EHの 交点をK，Kを通り，JKに垂直 な直線とDE，FGの交点をそれ ぞれL，Mとすると，△JLMは 正三角形になることを証明せよ。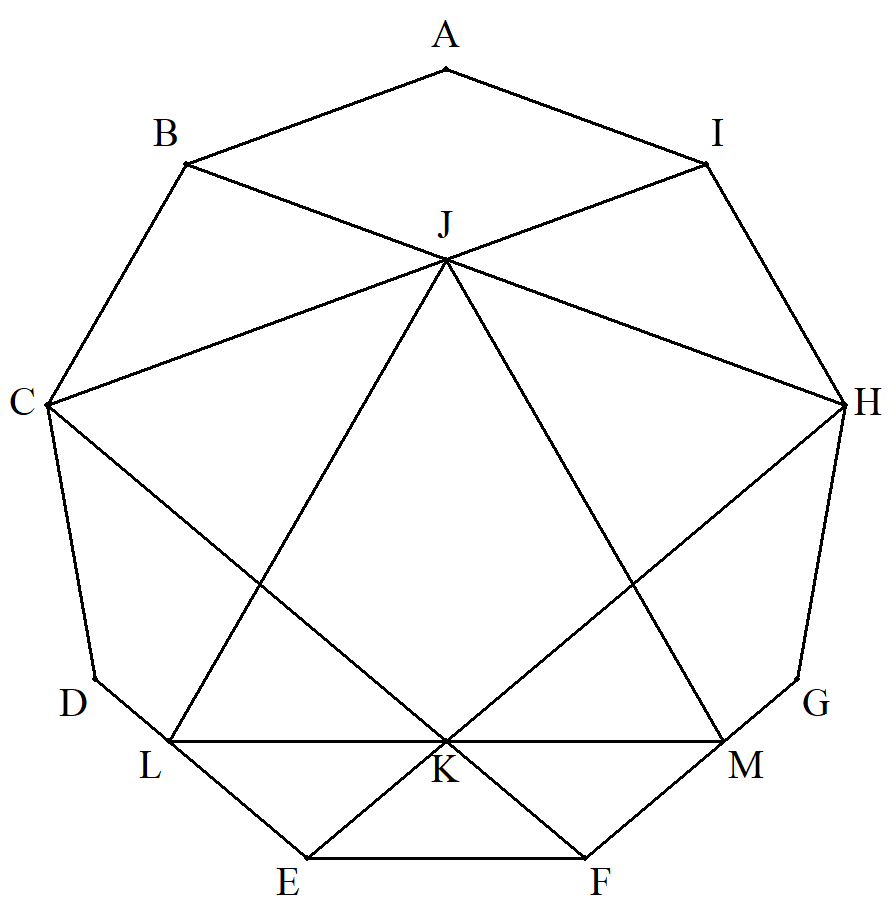

     
     
     
395. 
     

     半円内に直角三角形を描き，その中へ 甲円1個，乙円2個を入れる。 乙円径を甲円径で表せ。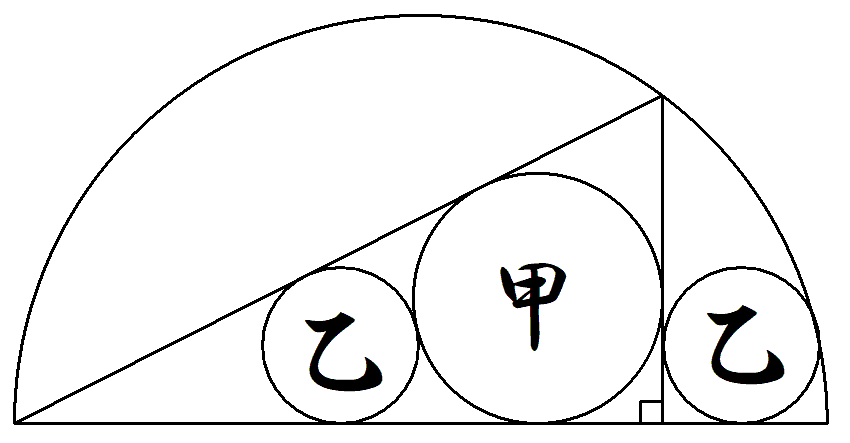

     
     
     
396. 
     

     半円内に直角三角形を描き，その中へ 甲円1個，乙円2個を入れる。 直角三角形の高さを底辺で表せ。

     
     
     
397. 
     
     
     
398. 
     
     
     
399. 
     
     
     
400.