| Oを原点として,平面上に n+1 個の点 A0,A1,A2,・・・,Anを次のようにとる. A0(1,0),∠Ai+1OAi=2π/n,∠OAiAi+1=π/2(i=0,1,2,・・・,n-1,n≧5) このとき,次の問いに答えよ. (1) 多角形A0A1A2・・・An(かたつむり形)の面積を求めよ. (2) 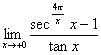 を求めよ. を求めよ. | 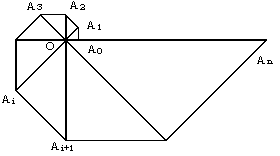 |
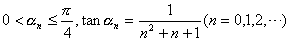 のとき,次の問いに答えよ.
のとき,次の問いに答えよ.(1) tanα0,tan(α0+α1),tan(α0+α1+α2) の値を求めよ.
(2) tan(α0+α1+…+αn-1) の値を求めよ.
(3) 無限級数
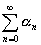 を求めよ.
を求めよ.
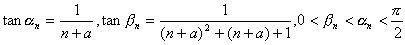
によって定義される.ただし,n=0,1,2,… で,定数 a はすべての n に対し
αn-βn≦3π/20
を満たす最小の整数である.このとき,次の問いに答えよ.
(1) cot 3π/20 の値を求め,その近似値を小数第2位まで計算せよ.
(2) a の値を求めよ.
(3) tan(α0-α1) ,tanβ0 ,tan(α1-α2) ,tanβ1の値を求めよ.
(4) 無限級数
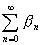 を求めよ.
を求めよ.(5) 無限級数
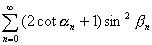 を求めよ.
を求めよ.
(1)
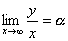
(2)
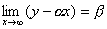
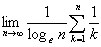 を求めよ.
を求めよ.
(1)
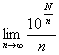 を求めよ.
を求めよ.(2)
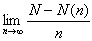 を求めよ.
を求めよ.

(1) P(n,m) を求めよ.
(2)
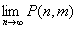 を求めよ.
を求めよ.(3) 任意のn の値に対して,P(n,m)≧0.01 となる最大の m の値を求めよ.
ただし,log101.09=0.0374 とする.
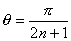 のとき,
のとき,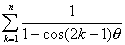 の値を求めよ.
の値を求めよ.
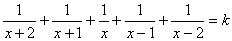 (定数)について,次の問いに答えよ.
(定数)について,次の問いに答えよ.(1) k>0 のとき,正の解3個,負の解2個もつことを証明せよ.
(2) K=0 のとき,解を求めよ.
(1)
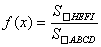 を求めよ.
を求めよ.(2) f(x) の最大値と,そのときのxの値を求めよ.
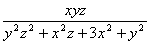 の最大値を求めよ.
の最大値を求めよ.
(1) y=sin x,y=cos x,y=tan x
(2) y=cos x,y=tan x,y=cot x,y=sec x
(3) y=cot x,y=sec x,y=cesec x
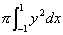 の値を求めよ.
の値を求めよ.
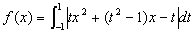 について,次の問に答えよ.
について,次の問に答えよ.(1) f(-x)=f(x) を証明せよ.
(2) f(x) を求めよ.
(3) f(x) の最小値を求めよ.
(4)
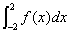 を求めよ.
を求めよ.
1
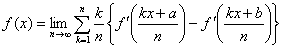
2 f(0)=0
3 f '(0)=b-a=c≠0
4
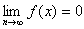
(1) f(x) の最大・最小値と,そのときの x の値を求めよ.
(2) 曲線 y=f(x) と x軸との間の部分の面積を求めよ.
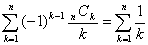 を証明せよ.
を証明せよ.
(1)
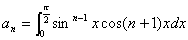 のとき,
のとき,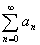 を求めよ.
を求めよ.(2)
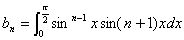 のとき,
のとき,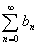 を求めよ.
を求めよ.
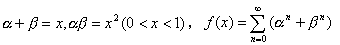 とおくとき,次の問いに答えよ.
とおくとき,次の問いに答えよ.(1) f(x) を求めよ.
(2) f(x) の最大値と,そのときの x の値を求めよ.
(3) 区間[0,1]におけるf(x) の平均値を求めよ.ただし,f(0)=2,f(1)=1 と定義する.
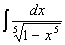 を求めよ.
を求めよ.
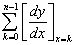 を求めよ.
を求めよ.
(1)
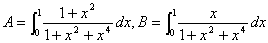
(2)
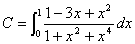
(1) ①が実数解だけをもつとき,点 (a,b) の存在する範囲を図示せよ.
(2) kを正の定数として,0≦b/k≦a≦1 を満たす任意の a,b を選んだとき,①が実数解しかもたない確率 P(k) を求めよ.
(3) (2)で P(k)の最大値と,そのときの k の値を求めよ.
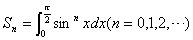 とおくとき,次の問いに答えよ.
とおくとき,次の問いに答えよ.| (1) | ① | S0,S1 の値を求めよ. |
| ② | Sn,Sn-2の関係式を求めよ. | |
| ③ | nSn-1Sn の値を求めよ. | |
| ④ | 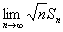 の値を求めよ. の値を求めよ. |
|
| (2) | ① | cosx=y とおくと,S2m+1 はどうなるか. |
| ② | cotx=y とおくと,S2m-2はどうなるか. | |
| ③ | 1-y2≦e-y2≦1/(1+y2) を証明せよ. | |
| ④ | 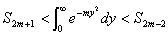 を証明せよ. を証明せよ. |
|
| ⑤ | 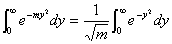 を証明せよ. を証明せよ. |
|
| (3) | ① | 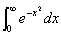 の値を求めよ. の値を求めよ. |
| ② | 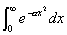 の値を求めよ. の値を求めよ. |
|
| ③ | 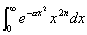 の値を求めよ. の値を求めよ. |
|
| ④ | 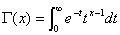 とおくとき, とおくとき,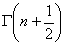 の値を求めよ. の値を求めよ. |
| 棒を水平に持って幅 a メートルの廊下から,それに直角な幅 b メートルの廊下に曲がりたい. これが可能であるための棒の最大の長さを求めよ. | 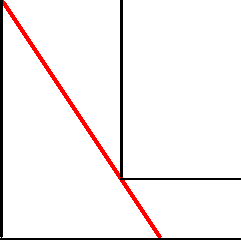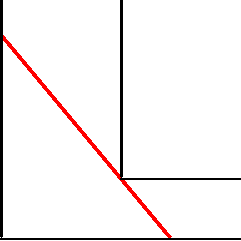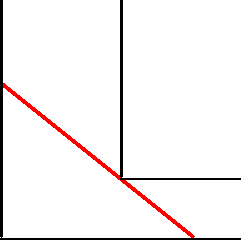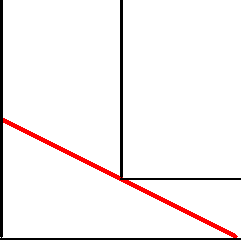 |
| 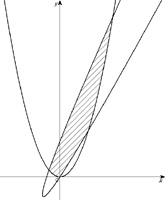 |
|
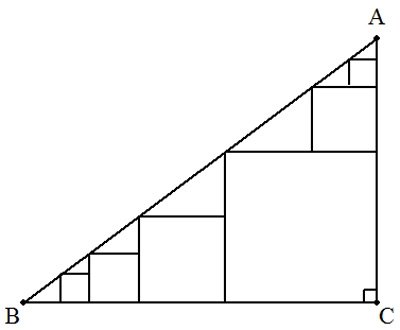
∠Cが直角の直角三角形ABC内に,図のように連結する無限個の内接正方形を考える。 (1) BC=4,AC=3とするとき,これらすべての正方形の面積の和を求めよ。 (2) BC=a,AC=bとするとき,これらすべての正方形の面積の和を求めよ。 |
 |
|
(1) ∠Cが直角の直角三角形ABC内に,図のように直角三角形ABCの内接円から3つの頂点に向かって連結した無限個の内接円を考える。 BC=4,AC=3のとき,これらすべての円の面積の和を求めよ。 | 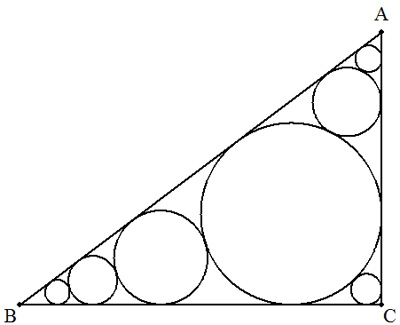 |
| (2) (1)で,BC=a,AC=bのとき,これらすべての円の面積の和を求めよ。 | |
| (3) 三角形ABC内に,図のように直角三角形ABCの内接円から3つの頂点に向かって連結した無限個の内接円を考える。 BC=a,CA=b,AB=cのとき,これらすべての円の面積の和を求めよ。 | 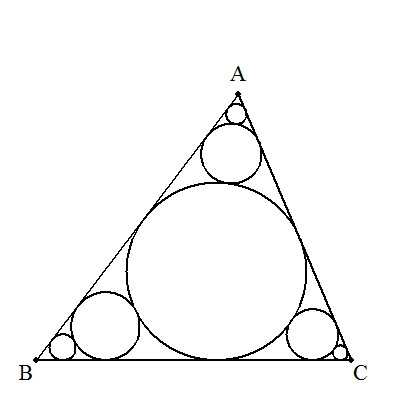 |
|
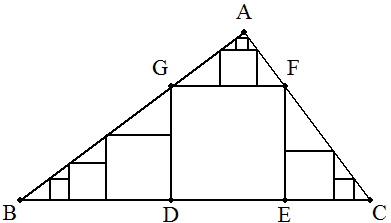
BC=5,CA=3,AB=4の⊿ABC内に,図のように正方形DEFGを内接させる。 また,図のように⊿AGF内,⊿GBD内,⊿FCE内にそれぞれ連結する無限個の内接正方形を考える。 このとき,これら⊿ABC内のすべての正方形の面積の和を求めよ。 |
 |
|
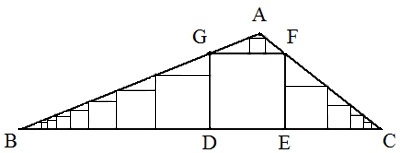
BC=7,CA=3,AB=5の⊿ABC内に,図のように正方形DEFGを内接させる。 また,図のように⊿AGF内,⊿GBD内,⊿FCE内にそれぞれ連結する無限個の内接正方形を考える。 このとき,これら⊿ABC内のすべての正方形の面積の和を求めよ。 |
 |
|
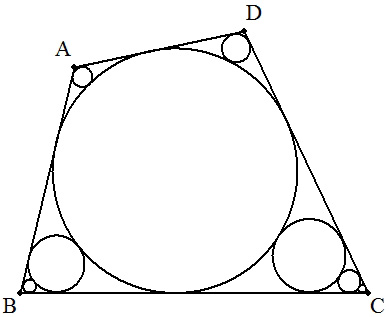
円に内接する四角形ABCDの内接円から4つの頂点に向かって連結した無限個の内接円を考える。 AB=4,BC=6,CD=5,DA=3のとき,これらすべての円の面積の和を求めよ。 |
 |
|
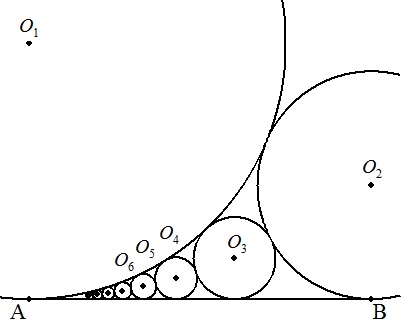
半径9の円O1と半径4の円O2が外接していて,線分ABは2円の共通接線である。 線分ABに接して,2円O1,O2に外接する円をO3, 線分ABに接して,2円O1,O3に外接する円をO4 , 以下同様に円O5,O6,・・・を考える。 このとき,円O3,O4,O5,・・・ すべての面積和 を求めよ。 |
 |
半径r,高さhの円錐に球O1が内接している。
球O1に外接し,円錐に内接する球をO2,
球O2に外接し,円錐に内接する球をO3,
・・・と,円錐の頂点に向かって連結する無限個の球を考える。
このとき,円錐内のすべての球の体積をr,hを用いて表せ。
| (1) | 一辺aの正方形の中に合同な正方形を図のようにn段内接させる(図は3段)。 n→∞のとき,合同な正方形の面積の和を求めよ。 | 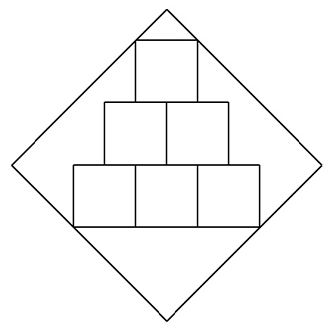 |
| (2) | 一辺aの正三角形の中に合同な正方形を図のようにn段内接させる(図は3段)。 n→∞のとき,合同な正方形の面積の和を求めよ。 | 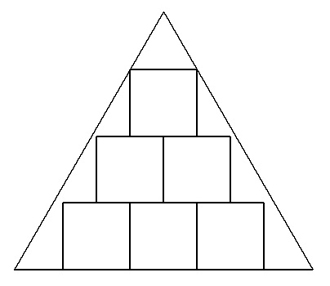 |
| (3) | 半径rの円の中に合同な正方形を図のようにn段内接させる(図は3段)。 n→∞のとき,合同な正方形の面積の和を求めよ。 | 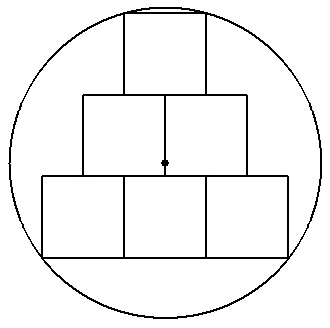 |
| (4) | 一辺aの正五角形の中に合同な正方形を図のようにn段内接させる(図は3段)。 n→∞のとき,合同な正方形の面積の和を求めよ。 | 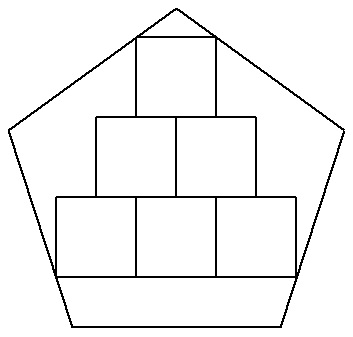 |
| (5) | 一辺aの正六角形の中に合同な正方形を図のようにn段内接させる(図は3段)。 n→∞のとき,合同な正方形の面積の和を求めよ。 | 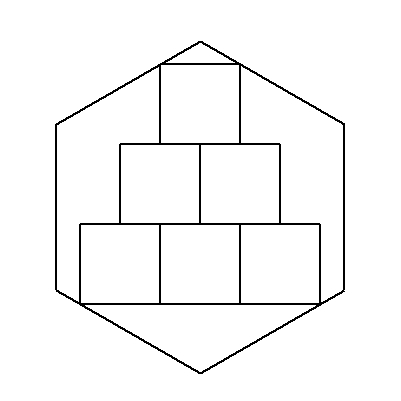 |
|
正方形の折り紙ABCDにおいて,頂点AをBC上の点Gに重ねて折ったとき, 頂点DはHに移り,折り目をEF,GHとCDとの交点をIとする。さらに, △EBG,△GCIの内接円をそれぞれJ,Kとし,それらの半径をr,Rとする。 正方形の1辺の長さを1とするとき, (1) R-rの最大値を求めよ。 (2) 円Kの面積-円Jの面積が最大になるとき,BGの長さを求めよ。 | 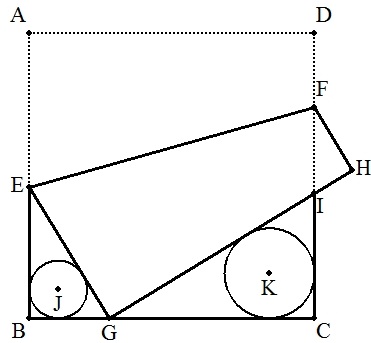 |
|
△ABCのBC上に動点Pをとり, ACの中点をM,BMとAPの交点をQ, 頂点BからACに下ろした垂線BHとAPの交点をR, ∠Bの2等分線とAC,APの交点をそれぞれD,Sとする。 次の条件を満たすBPの長さを求めよ。 ただし,BC=a,CA=b,AB=cとする。 (1) △AMQ+△BPQが最小 (2) △AHR+△BPRが最小 (3) △ADS+△BPSが最小 | 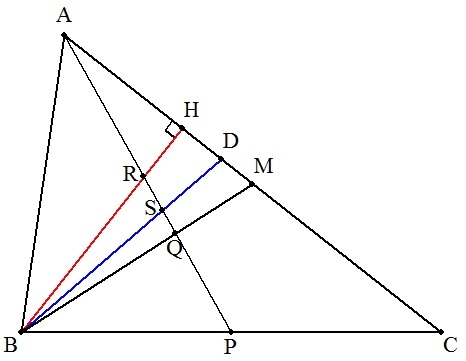 |
次の等式を証明せよ。
| (1) | |
| (2) | |
|
三角形OABのOA上にn個の点A1,A2,・・・,AnをOに近い ところから,OB上にn個の点B1,B2,・・・,BnをOに近い ところから,⊿OA1B1 =⊿A1B1B2=⊿A1A2B2 =⊿A2B2B3=⊿A2A3B3 =⊿A3B3B4=⊿A3A4B4 ・・・・・・・・・・・・・・・・・・・・・ =⊿AnBnB=⊿AnAB となるようにとる。 OA=a,OB=bのとき, 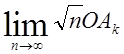 および 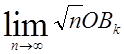 (k=1,2,3,・・・,n)の極限値を求めよ。 | 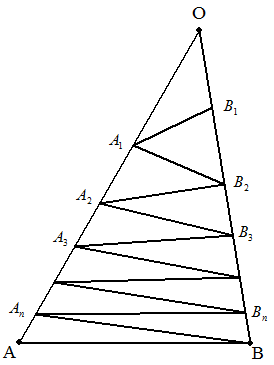 |
xについての方程式 |n|n|nx-1|-1|-1|=x2 ・・・①
について,次の問に答えよ。
(1) n=2のとき,①を解け。
(2) n>2のとき,①の解のうち,最大のものα,および,最小のものβを求めよ。
(3) (2)で,n→∞とするとき,n(α+β)の極限値を求めよ。
|
二等辺三角形ABCの辺BCの中点をMとする。 この三角形の内接円をO1(r1), 円O1に外接し,AB,AMに接する円をO2(r2),AC,AMに接する円をO2'(r2), 2円O2,O2'に外接し,AB,ACに接する円をO3(r3), 円O3に外接し,AB,AMに接する円をO4(r4),AC,AMに接する円をO4'(r4), ・・・,と連結する円を三角形ABC内に描いていく。 AB=25,BC=14のとき,これらすべての円の面積和を求めよ。 | 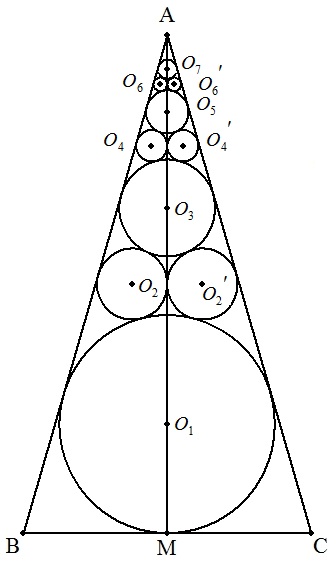 |
aを1でない正の定数とするとき,
1/{1+(1-a)x-ax2}=a0+a1x+a2x2+・・・+an-1xn-1+・・・
とおくとき,a0+a1+a2+・・・+an-1の値を求めよ。
|
C=90°である△ABCのCA,AB,BC上にそれぞれ点D, E,Fを,四角形CDEFが正方形になるようにとる。 △EBF-△AEDが最大になるのは,どのようなときか。 | 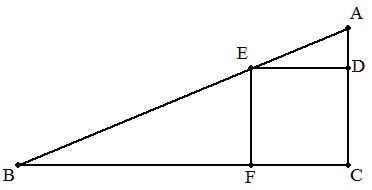 |
|
座標平面上に,定点P(3,1)がある。いま,x軸上の正の部分に 点Aをとり,APと直線y=(56/33)xとの交点をBとする。 (1) ABの長さが最小になるとき,点Aの座標を求めよ。 (2) (1)のとき,OからABに下ろした垂線の足をQとするとき, APとBQの大小を比較せよ。 | 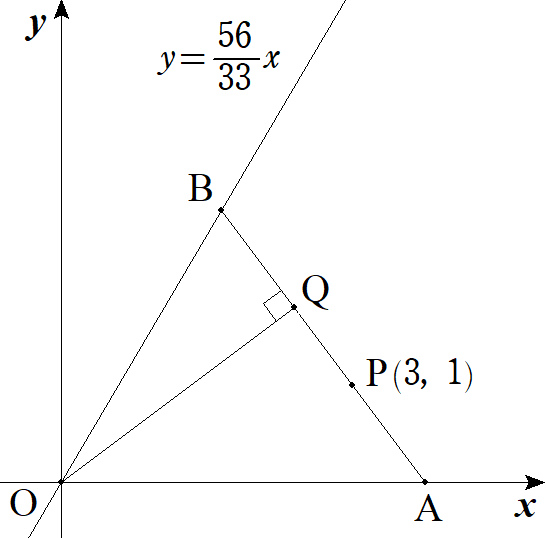 |