■趣味の数学問題集・Ａ問題の答

---

251. 
     

     （作図） 大円周上に任意に点Aをとる。 点Aから小円に接線を1本引き，接点を Tとする。 点Aから∠ATOの二等分線に下ろした 垂線の足をHとする。 点Aを中心，半径AHの円と小円との 交点の一方をBとする。 ABの延長が再び小円と交わる点をC， さらに，大円と交わる点をDとすれば 求める大円の弦ADが作図できる。 （証明） 大円，小円の半径をそれぞれr1，r2とする。 すなわち，OA＝r1，OB＝OC＝r2 いま，AB＝BC＝xとおき，△OCAに中線定理を適用すると， r12+r22＝2(ｘ2＋r22) x>0より，x＝√(r12-r22)/√2　･･･① また，AT＝√(OA2－OT2)＝√(r12－r22)　･･･② ①，②より　AB：AT＝1：√2 よって，ABを1辺とする正方形の対角線がATとなるから， 上記の作図で求める大円の弦ADが作図できる。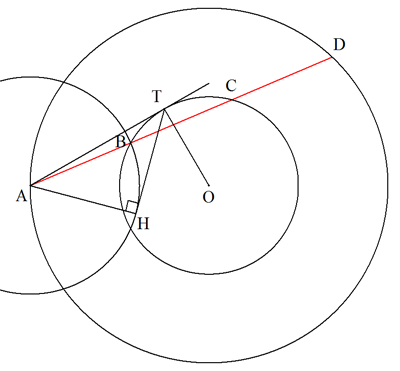

252. 
     

     線分ACを1:2に内分する点Eと， 外分する点Fを直径の両端とする 円（アポロニウスの円）と 線分BDを3:4に内分する点Gと， 外分する点Hを直径の両端とする 円（アポロニウスの円）との交点のうち， 正方形内の点をPとすればよい。 （補足） A(0,1)，B(0,0)，C(1,0)，D(1,1)のとき， P(3(-46+11√39)/274,3(79-4√39)/274)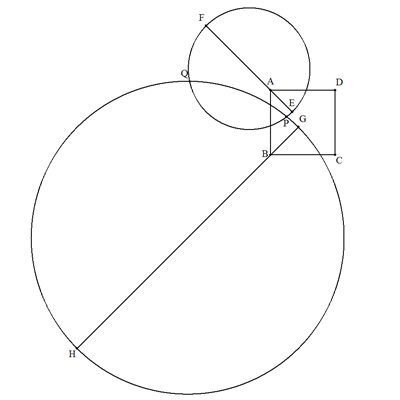

253. 
     

     円Aのlに関する対称な円をCとし， 2円C，Bの共通接線LEを引いて， lと交わる点をPとし，Pを求めてから 円に接線PD，PEを引けばよい。 また，一般に，共通接線は4本ある から，題意を満たす点は4つある。 図では，P，Q，R，S。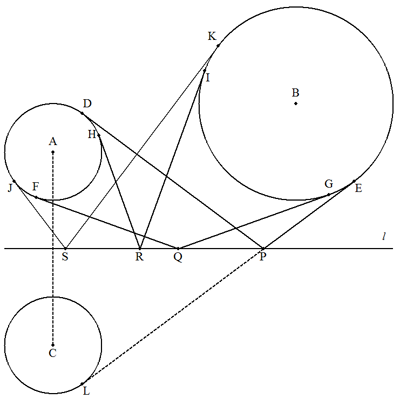

254. 
     (1)　4√2)
     (2)　1：2
     解答例→こちら
     
255. 
     

     （証明） 2円O，Pの半径をそれぞれr1，r2，OP＝dとする。 接点に図のように記号をつけ，弦AB，CDとOPとの交点を それぞれI，Jとすると，AI＝IB，CJ＝JDである。 △AOI∽△POGより　OA：OP＝AI：PG r1：d＝AI：r2より　AI＝r1r2/d ∴AB＝2r1r2/d　･･･① 同様に，△CPJ∽△OPEより　PC：PO＝CJ：OE r2：d＝CJ：r1より　CJ＝r1r2/d ∴CD＝2r1r2/d　･･･② ①，②より　AB＝CD（終証）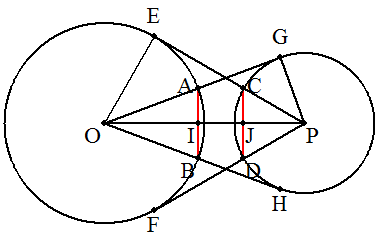

256. 
     

     ＜マッシェローニの作図＞ ①AおよびBを中心として，半径ABの円を描き， 交点の1つをCとする。 ②同じ半径でCを中心の円とBを中心の円との 交点のうちAでない方をDとする。 ③同じ半径でDを中心の円とBを中心の円との 交点のうちCでない方をEとする。 ④Aを中心，半径AEの円とEを中心，半径ECの 円との交点をF，Gとする。 ⑤FおよびGを中心としてEを通る円を描くと， その交点のうちEでない方が求めるABの中点 Mである。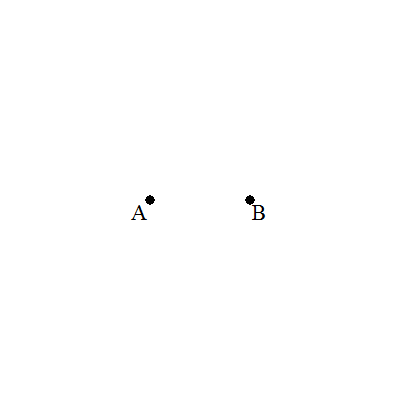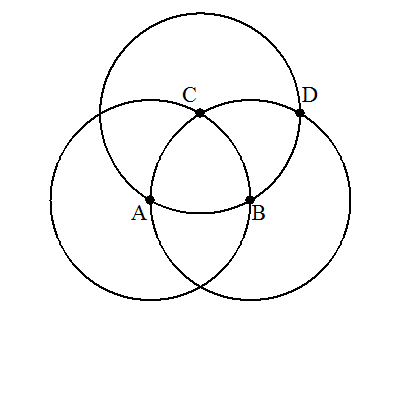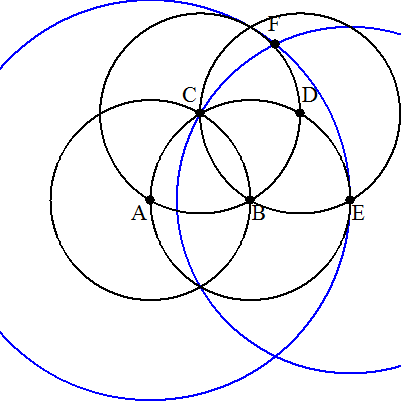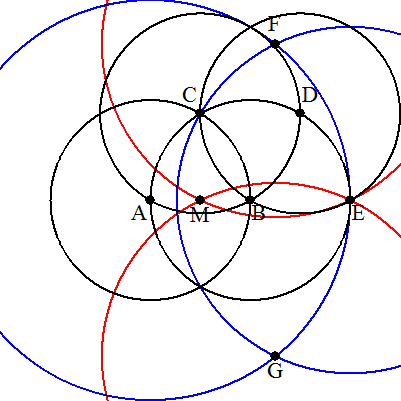

257. 
     

     DCの延長上にAC∥BGとなる点Gをとる。 DEの延長上にAE∥FHとなる点Hをとる。 GHの中点をMとし，AD∥MPとなる点Pを 辺上にとればよい。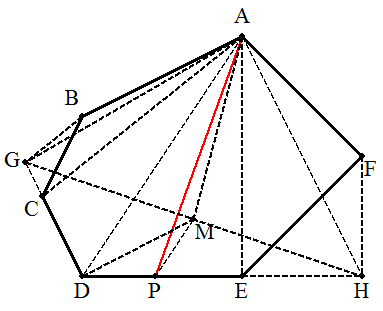

258. 
     解答例→こちら
     
259. 
     

     弦の長さを用意するために，POの延長上に点Qを 2PO＝PQ＝8となるようにとる。 PQの長さで弦RSを任意に作図する。 点Oを中心とし，弦RSに接する円①を描く。 点Pを通り円①に接する直線が円Oとの交点をA，Bとする。 図のように2通り作図ができる。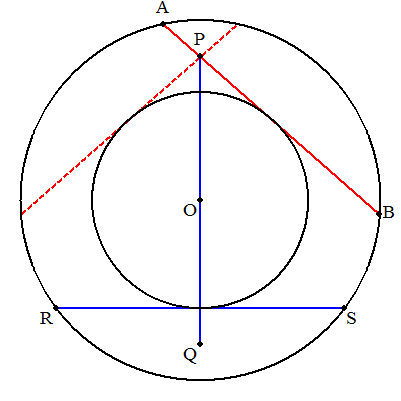

260. 
     

     2円の中心であるO，Pの中点をMとする。 Mを中心に半径AMの円を描き，円Pとの 交点のうち，図に示した方をDとする。 ADを引き，B，Cが求められる。 （証明） O，PからADに下ろした垂線の足をそれ ぞれE，Fとすると，AE＝BE，CF＝DF， OE∥PFとなる。 点NをEF上に，OE∥MNとなるようにとる。 MはOPの中点であるから， NはEFの中点となるので，EN＝FN　･･･① また，△AMN≡△DMNより　AN＝DN　･･･② ①，②より　AN－EN＝DN－FN AE＝FD よって　AB＝CD（終証）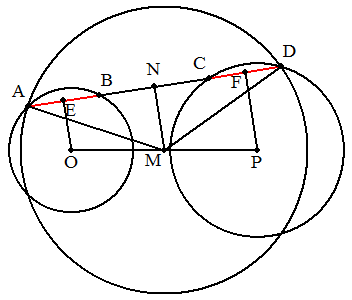

261. 
     （解）同じ数に分けられるためには，nは3の倍数でなければならない。
     その確率1/3。
     n個のボールを1列に並べ，仕切りを2個所入れて3つに分ける場合の数は
     _n+2C₂＝(n+2)(n+1)/2
     よって求める確率は積の法則より
     (1/3)×1/{(n+2)(n+1)/2}＝2/{3(n+1)(n+2)}　･･･（答）
262. 
     (1)　(7-5√2-4√3+3√6)r
     (2)　(-7-5√2+4√3+3√6)r
     
     
263. 
     

     （作図） 線分AB，CDを直径とする円を作る。 図のように，半円弧の中心をそれぞれM，Nとする。 直線MNをそれぞれ他の半円弧とP，Rで交わらせ， PB，RCの交点をQ，PA，RDの交点をSとすれば， 四角形PQRSが求める正方形となる。 （証明） △PQRについて， ∠QPR＝∠BPM＝∠BAM＝45° （∵△MABは直角二等辺三角形） 同様に，∠QRP＝∠CRN＝∠CDN＝45° （∵△NCDは直角二等辺三角形） よって　△PQRは直角二等辺三角形 同様に，△PSRも直角二等辺三角形 しかも，△PQR≡△PSR 四角形PQRSは4辺が等しく，対角がそれぞれ90° であるから，正方形となる。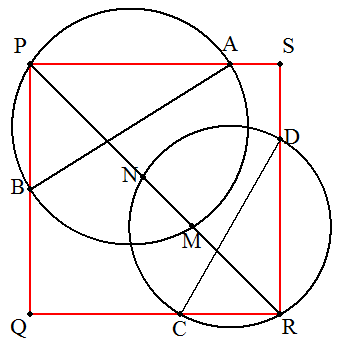

264. 
     

     与えられた円をOとする。 PQの中点Mを中心，半径PMの円と円Oとの交点をA，Dとする。 AP，AQと円Oとの交点をそれぞれB，Cとすると， △ABCは直角三角形となる。 同様に，DP，DQと円Oとの交点をそれぞれE，Fとすると， △DEFは直角三角形となる。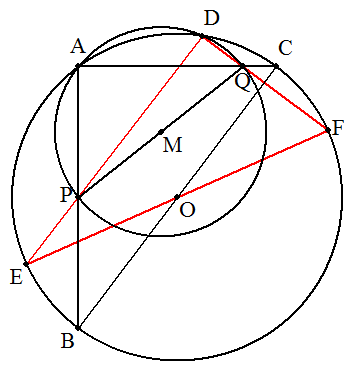

265. 
     

     点Bを通る直線を図のようにEFとし， 線分EFの中点をMとする。 一方の円周上の点Cを， CE∥AMとなるようにとり， CAともう一方の円との交点を Dとすれば，AC＝ADとなる。 （証明） ∠CEB＝∠AMF　･･･①（CE∥AM） ∠CEB＝∠BAD（四角形ACEBは円に内接する） 　　　＝∠DFG　･･･② （GはBFの延長上の点で，四角形ABFDは円に内接する） ①，②より ∠CEB＝∠AMF＝∠DFGであるから CE∥AM∥DF よって，ME＝MFであるからAC＝AD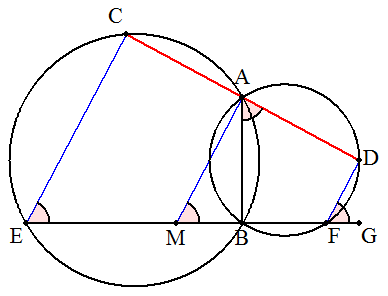

266. 
     

     AからBCに下ろした垂線の足をHとし，AHの中点を Mとする。 BCの延長上に点Nを，CN＝HMとなるようにとる。 BNの中点Pを中心，半径BPの円を描く。 円周上の点DをDC⊥BCとなるようにとる。 このとき，CDが求める正方形の一辺となる。 （証明） 図で，△DBC∽△NDCであるから DC2＝BC・CN BC＝a，AH＝hとおくと，△ABC＝(1/2)ah また，DC2＝a(h/2)＝(1/2)ah＝△ABC よって，DCは求める正方形の一辺となる。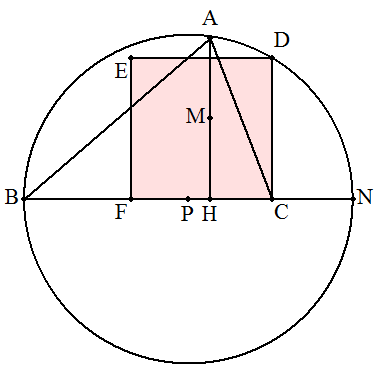

267. 
     

     点Aを通り，BCに平行な直線上に，点Fを ∠FCB＝60°となるようにとる。 BC上に，CF＝CGとなる点Gをとると， △CFGは正三角形となる。 BGを直径とする円に接線CTを引く。 Cを中心，半径CTの円を描き，CFの延長と の交点をD，BCとの交点をEとすると， △CDEは求める正三角形となる。 （証明） △ABC＝△FBC（等積変形） △CDE/△FBC＝CD・CE/CF・CB＝CT2/CG・CB＝1 （方べきの定理より） よって　△ABC＝△CDE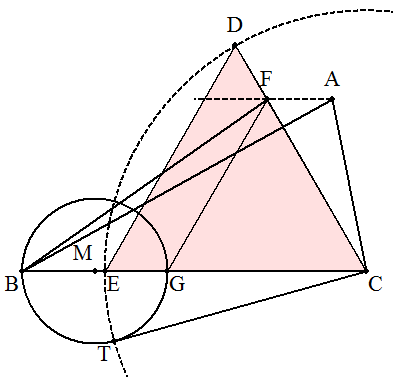

268. 
     

     （証）＜中学生向け＞ 便宜上，BC＝a，CA＝b，AB＝cとおくと， c2＝a2＋b2である。 CBの延長上に点Jを，BJ＝aとなるようにとり， CAの延長上に点Kを，AK＝bとなるようにとる。 △BDG≡△BAJ（2辺夾角相等）より，DG＝AJ △AHE≡△AKB（2辺夾角相等）より，EH＝BK DG2＋EH2 ＝JA2＋BK2 ＝（JC2＋CA2）＋（BC2＋CK2） ＝｛（2a）2＋b2｝＋｛a2＋（2b）2｝ ＝5（a2＋b2） ＝5c2 ＝5AB2　（終証） （別証）＜高1向け＞ cosA＝b/c，cosB＝a/c △BDGに余弦定理を適用すると DG2＝c2＋a2－2cacos(180°－B)＝3a2＋c2 同様に，△AHEについて EH2＝b2＋c2－2bccos(180°－A)＝3b2＋c2 DG2＋EH2 ＝3a2＋c2＋3b2＋c2 ＝3（a2＋b2）＋2c2 ＝5c2 ＝5AB2　（終証）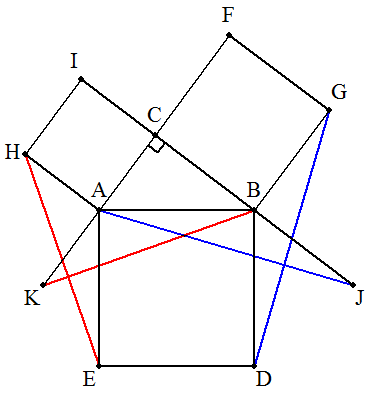

269. 
     (1)　30通り
     (2)　174通り
     (3)　1080通り
     解答例→こちら
     
270. 
     

     （作図） 点BからACに下ろした垂線の足をHとする。 HCを直径とする円に接線ATを引く。 ただし，Tは接点である。 AC上に点Eを，AE＝ATとなるようにとる。 ABの延長上に点Dを，DE⊥ACとなるようにとる。 このとき，△ABC＝△ADE （証明） 方べきの定理より AT2＝AH・AC AT＝AEであるから AE2＝AH・AC 変形すると AE/AC＝AH/AE　…① ここで，△ABH∽△ADEであるから AH/AE＝BH/DE　…② ①，②より AE/AC＝BH/DE (1/2)AE・DE＝(1/2)BH・AC よって △ADE＝△ABC（終証）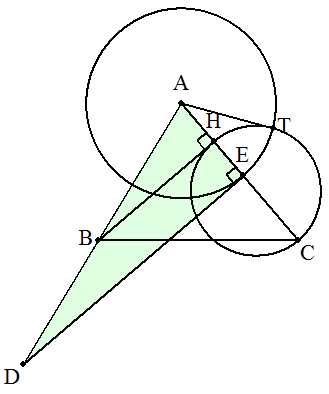

271. 
     

     (1) EDの延長上に点FをBF∥ADとなるようにとり， DEの延長上に点GをCG∥AEとなるようにとる。 このとき，五角形ABDEC＝△AFG（等積変形）となるので， FGの中点をPとすれば，APは五角形を二等分する。 (1)（別解）BC，DEの中点をそれぞれM，Nとおくと， 線分AM，MNで五角形の面積は二等分される。 よって，DE上に点Pを，MP∥ANとなるようにとると， 線分APは五角形を二等分する。 (2) AからDEに下ろした垂線の足をH， BCとAH，AD，AEとの交点を順にI，J，Kとする。 △ABCにおいて，CA＝2aとおくと，仮定より AB＝2√3a，BC＝4a，∠CAB＝90° また，AI＝√3a，BI＝3a，IC＝aとなる。 今，FD＝BJ＝x，EG＝KC＝yとおくと， △BDJ∽△IAJより，x：(3a－x)＝4a：√3a ∴　x＝12a/(4＋√3)…① 同様に，△CEK∽△IAKより，y：(a－y)＝4a：√3a ∴　y＝4a/(4＋√3)…② DP＝FP－x＝FG/2－x＝(x＋4a＋y)－x＝{4a－(x－y)}/2 PE＝4a－DP＝{4a＋(x－y)}/2 ①，②より　x－y＝8a/(4＋√3)であるから DP：PE＝{4a－8a/(4＋√3)}/2：{4a＋8a/(4＋√3)}/2 ＝(2＋√3)：(6＋√3)＝1：(9－4√3) よって　k＝9－4√3　…（答）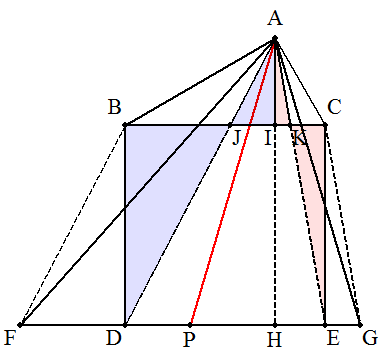

272. 
     

     (1) BC，DEの中点をそれぞれM，Nとおくと， 線分AMとMNで五角形の面積は二等分される。 よって，DE上に点Pを，MP∥ANとなるようにとると， 線分APは五角形の面積を二等分する。 (2) AI＝h，PN＝xとおくと， DP＝a/2－x，PE＝＝a/2＋x △MPN∽△ANHより，PN：MN＝NH：AH x：a＝(a/2－IC)：(a＋h) x＝a(a/2－IC)/(a＋h) DP＝a/2－a(a/2－IC)/(a＋h)＝(ah/2+a・IC)/(a＋h) ＝(S1＋S3)/(a＋h) PE＝a/2＋a(a/2－IC)/(a＋h)＝{ah/2＋a(a－IC)}/(a＋h) ＝(S1＋S2)/(a＋h) よって DP：PE＝(S1＋S3)/(a＋h)：(S1＋S2)/(a＋h) ＝(S1＋S3)：(S1＋S2)　（終証） 【補足】高校1年生なら，次式のようにも変形できる。 DP：PE＝(1＋2/tanC)：(1＋2/tanB) ∵）S1＋S3＝S1(1＋S3/S1) ＝S1(1＋a・bcosC/{(1/2)absinC})＝S1(1＋2/tanC) 同様に，S1＋S2＝S1(1＋2/tanB)と変形できる。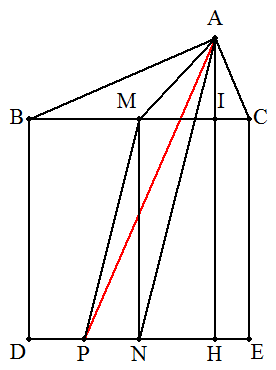

273. 
     

     PSなど4つの直線と正方形の4辺との交点を， 図のようにE，F，G，H，I，J，K，Lとする。 △SDNと△SBCにおいて，△SDN∽△SBCで， DN：BC＝1：2であるからSD：SB＝1：2 ∴DJ：JC＝1：2…①，DK：KA＝1：2…② 同様に，△QBM∽△QDAで BQ：QD＝1：2であるから ∴BF：FA＝1：2…③，BG：GC＝1：2…④ AD∥EJ∥FI∥BC，AB∥LG∥KH∥DCと①～④から E，F，G，H，I，J，K，Lは各辺の3等分点となる。 よって，正方形は4つの直線PS，QR，PQ，SRに よって9個の合同な正方形に分割される。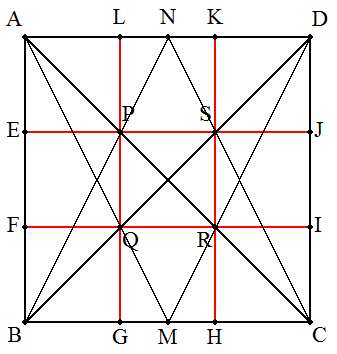

274. 
     

     AL⊥MNが証明できれば， ∠APM＝∠APN＝∠LPM＝∠LPN＝90°となるので， AM，AN，LM，LNを直径とする4円は1点Pで交わる。 いま，正方形ABDCをつくり，ALとDCとの交点を Eとすると，△LAB∽△LECである。 △AECについて， AC：EC＝AB：EC＝BL：CL＝m：n，∠ACE＝90°…① また，△NMAについて， NA：MA＝CM：MA＝m：n，∠NAM＝90°…② ①，②より，△AEC∽△NMAであるから，∠EAC＝∠MNA ∠APM＝180°－（∠MAP＋∠AMP） ＝180°－（∠MNA＋AMN） ＝180°－（180°－90°）＝90° 従って　AL⊥MNとなるので， AM，AN，LM，LNを直径とする4円は1点Pで交わる。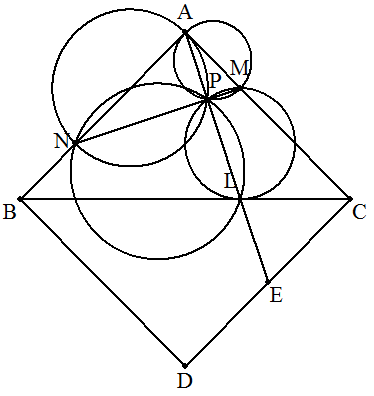

275. 
     

     4h1h2√(a12+b12)√(a22+b22)/|a1b2-a2b1| （補足）四角形は平行四辺形となる。 （例題）2直線x+2y-6=0…①，x-3y+4=0…② への距離がそれぞれ2，3である点を頂点と する四角形の面積を求めよ。 （答）24√2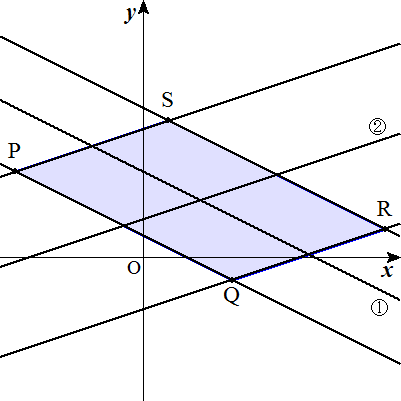

276. 
     

     △CHD≡△AGD（2角夾辺相等）であるから AG＝CH＝b，AH＝AC－HC＝(a+b)－b＝a △AGHに三平方の定理を適用して， GH＝√(a2+b2) △DHGは直角二等辺三角形であるから， GD＝GH÷√2＝√(a2+b2)/√2 次に，∠AFD＝∠ABD＝45°より， 四角形AFBDは円に内接する。 方べきの定理より，FG・GD＝AG・GB FG＝AG・GB/GD＝ab√2/√(a2+b2) FD＝FG＋GD＝ab√2/√(a2+b2)＋√(a2+b2)/√2 ＝(a+b)2/√{2(a2+b2)} よって　EF＝√2・FD＝(a+b)2/√(a2+b2)…（答） （例） BG＝4，CH＝3のとき，EF＝49/5 BG＝√3，CH＝1のとき，EF＝2+√3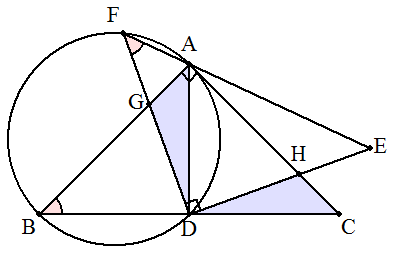

277. 
     (1)　XY＝10となる線分XYの中点をDとする。
     点Dを中心，半径3の円周上に点Eをとり，
     点Dを中心，半径4の円周上に点Fを，
     ∠EDF＝90°となるようにとる。
     EFを直径とする円と点Dを中心，半径BDの円（①）
     との交点が2個求まるので，A，A′とする。
     AF，AEと円①との交点をそれぞれB，Cとすると，
     △ABCが求めるものである。
     A′F，A′Eと円①との交点をそれぞれB′，C′
     とすると，△A′B′C′も求めるものである。
     (2)　△ABCと△DEFはともに直角三角形で
     　∠ABC＝∠DAF（△DABBLEは二等辺三角形）
     　　　　＝∠DEF（弧DFの円周角）
     よって　△ABC∽△DEF（2角相等）である。
     また，BC＝10，EF＝√(3²＋4²)＝5より
     相似比は，10：5＝2:1であるから
     面積比は，2²：1²＝4：1
     △DEF＝(1/2)×3×4＝6であるから
     △ABC＝6×4＝24…（答）
     （補足）
     一般に，BC＝a，DE＝e，DF＝fのとき　△ABC＝a²ef/2(e²+f²)
     
278. 
     (a²-t²)/(2√3)
     
279. 
     x₂=x₁-2a(ax₁+by₁+c)/(a²+b²)…①
     y₂=y₁-2b(ax₁+by₁+c)/(a²+b²)…②
     とおく。
     ①×a，②×bを辺々加え，cを補うと
     ax₂+by₂+c＝(ax₁+by₁+c)－2(ax₁+by₁+c)＝－(ax₁+by₁+c)
     これを①，②に代入し書き直すと，
     x₁=x₂-2a(ax₂+by₂+c)/(a²+b²)， y₁=y₂-2b(ax₂+by₂+c)/(a²+b²)
     が得られる。
     （補足）
     直線ax+by+c=0に関して，点(x₁,y₁)と対称な点を(x₂,y₂)とすると，①，②となる。
     こだわり数学　7「線対称な点を求める」を参照のこと。
     
280. 
     (1)　P，Qの秒速はそれぞれ，p√(d₀²-2d₁²+d₂²)/√{2(p²+q²)}，q√(d₀²-2d₁²+d₂²)/√{2(p²+q²)}
     (2)　√{(n-1)(n-2)d₀²-2n(n-2)d₁²+n(n-1)d₂²}/√2
     解答例→こちら
     
281. 
     略
     
282. 
     略
     
283. 
     (1)　略
     　任意のα，β∈Aに対して，αβ∈Aを示す。
     　こだわり数学64を参照せよ。
     (2)　略
     　任意のα，β∈Bに対して，αβ∈Bを示す。
     
284. 
     

     仮定より　∠GFE＝∠GDE･･･① ∠BEA＝∠BDA＝90°より 4点A，B，E，Dは同一円周上にある。 ∠BAE＝∠BDE＝∠GDE･･･② ①，②より ∠BAE＝∠GFEであるから　AB∥FG･･･③ CFの延長とABとの交点をHとすると △AFC≡△AFHであるから　FC＝FH ③より　CG：GB＝CF：FH＝1：1 よって，GはBCの中点である。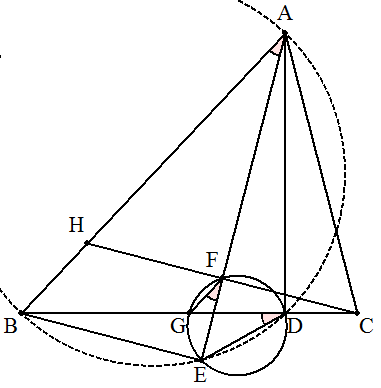

285. 
     (1)　4：1（△DEFを60°回転させる。）
     (2)　2：1（□EFGHを45°回転させる。）
     (3)　8：(3＋√5)　（正五角形FGHIJを36°回転させる。1：cos²36°を簡単にする。）
     
286. 
     （ヒント）
     まず，△AEF∽△ABCを証明する。
     次に，BC＝a，CA＝b，AB＝c，△ABC＝Sとおき，
     三角形の相似比を利用してEFを求める。
     EF＝4S²/abc。
     この値が，定数になることから，証明される。
287. 
     

     （証）△FBDを，点Fを中心に90°回転させ，△FGHとする。 まず，四角形HFDEが正方形となることを証明する。 ∠EDF＝∠DFH＝90°･･･①より DE∥FH･･･② 仮定より，DE＝FD＝FH･･･③ ②，③より，一組の対辺が等しく平行であるから， 四角形HFDEは平行四辺形となる。 ①より四角形HFDEは正方形となる。 次に，△ECDと△EGHについて CD＝BD＝GH･･･④ ED＝EH･･･⑤ ∠CDE＝180°－（90°＋∠BDF）＝180°－（90°＋∠GHF） ＝90°－∠GHF＝∠GHE ∠CDE＝∠GHE･･･⑥ ④～⑥より，2辺とその間の角がそれぞれ等しいから △ECD≡△EGH ∴　EC＝EG 四角形AFGEについて ∠AEG＝360°－(∠EAF＋∠AFG＋∠FGE) ＝360°－{∠A＋90°＋(∠B＋∠C）}＝90° よって△AEGは直角三角形となる。 また，△AFGも△AEGの斜辺を共有する直角三角形であるから AE2＋EG2＝AF2＋FG2 ここで，EG＝EC，FG＝FBであるから， AE2＋EC2＝AF2＋FB2（終証）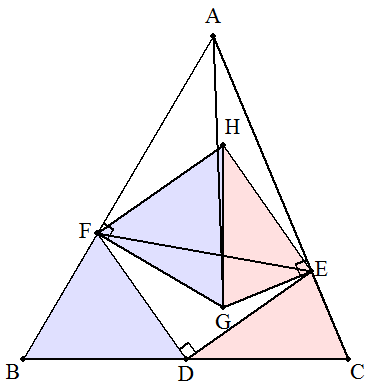

288. 
     (1)　DE＝3√10/2
     (2)　S＝117/2
     （前問の定理より，FB＝5）
     
289. 
     円弧　x²+(y-1)²=2　(－1＜x＜1，y＞0)
     
290. 
     

     仮定より，4点C，E，F，BはDを中心とする同一円周上にある。 四角形CEFBの内角は，対角の外角に等しいから ∠B＝∠AEF･･･① △DCEは二等辺三角形であるから，∠C＝∠DEC･･･② ∠EAF＝∠A＝180°－(∠B＋∠C) ＝180°－(∠AEF＋∠DEC)　∵①，②より ＝∠FED＝∠EFD　∵△DEFは二等辺三角形より よって　∠EAF＝∠FEDとなるから，接弦定理の逆より DEは△AEFの外接円の接線となる。 同様に，∠EAF＝∠EFDとなるから，接弦定理の逆より DFは△AEFの外接円の接線となる。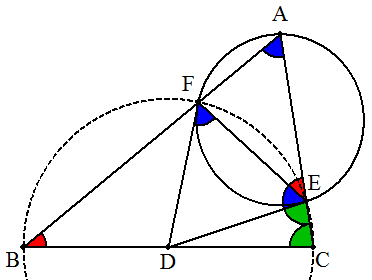

291. 
     △AFG：△ADE：△HDG：△HFE＝sin²B：sin²C：cos²B：cos²C
     
292. 
     

     (1)　BFA＝5 右の図で，AB2＋FC2＝AC2＋FB2となる。 点Gを四角形BGCFが平行四辺形となるよ うにとると，三平方の定理より明らか。 (2)　BC＝3√5 四角形ABGCは円に内接するので，トレミー の定理を使うと簡単。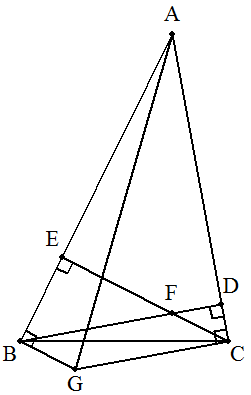

293. 
     (1)　a，b，c，dを自然数とし，2つの自然数の平方和を，a²＋b²，c²＋d²とおく。
     　(a²＋b²)(c²＋d²)＝(ad－bc)²＋(ac＋bd)²＝(ac－bd)²＋(ad＋bc)²より証明される。
     (2)　21²＋928²，144²＋917²，188²＋909²，280²＋885²，307²＋876²，395²＋840²，435²＋820²，540²＋755²
     の8通り。
     （参考）こだわり数学 64.平方和の積 参照
     
294. 
     RS＝6
     （補足）等式PQ/QC＝RS/CRが成り立つことが，方べきの定理より証明できる。
295. 
     

     AB＝13 （一般に）AD＝p，BD＝q，CD＝rのとき， 頂点Aを中心，半径ABの円を描き， ADと円との交点をE，Fとする。 AB＝xとおくと，方べきの定理より DE・DF＝DB・DC (x－p)(x＋p)＝qr x2＝p2＋qr x＞0より x＝AB＝√(p2＋qr)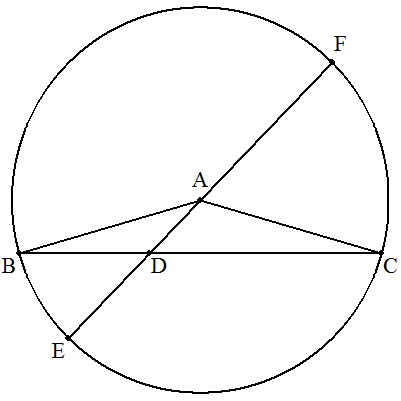

296. 
     

     （作図） 2円の接点をC， OC上に点DをCP＝CDとなるようにとり， OPの中点をEとする。 中心O，半径ODの円と中心E， 半径OEの円との交点をFとする。 OFの延長と円Oとの交点をA， FPに垂直で点Pを通る直線と円Pとの交点を 図のようにBとすると， 線分ABが共通接線となる。 （証明） OPは，円Eの直径であるから∠OFP＝90°･･･① ∠FPB＝90°（仮定）･･･② ①，②よりAF∥BP･･･③ また，仮定より，AF＝CD＝CP＝BP･･･④ ①，③，④より，四角形AFPBは長方形となる。 よって　OA⊥AB，PB⊥ABより， 線分ABは，2円の共通接線となる。 ※OPに関して線対称に作図すると，もう一つの共通接線が引ける。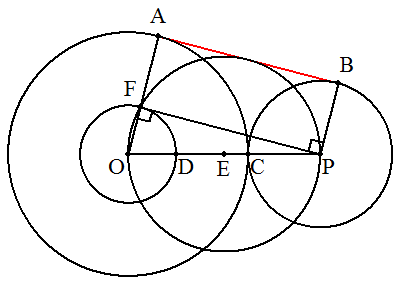

297. 
     

     (1)　線分OPと円O，Pとの交点をそれぞれC，Dとする。 OC上に点Eを，PD＝CEとなるようにとり，OPの中点をFとする。 Oを中心，半径OEの円と円Fとの交点をGとすると， ∠OGP＝90°となる。 OGの延長と円Oとの交点をA，図のように，GPに垂直で点Pを 通る直線と円Pとの交点をBとすると，ABが2円O，Pの 共通外接線となる。 ※OPに関して線対称に作図すると，もう一つの共通接線が引ける。 ※証明は，前問296と同様なので省略する。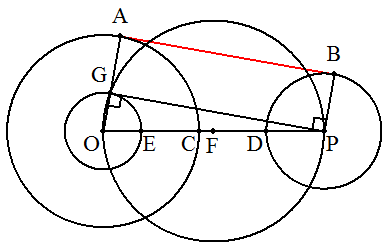
     (2)　線分OPと円O，Pとの交点をそれぞれC，Dとする。 CP上に点Eを，PD＝CEとなるようにとり，OPの中点をFとする。 Oを中心，半径OEの円と円Fとの交点をGとすると， ∠OGP＝90°となる。 線分OGと円Oとの交点をA，図のように，GPに垂直で点Pを 通る直線と円Pとの交点をBとすると，ABが2円O，Pの 共通内接線となる。 ※OPに関して線対称に作図すると，もう一つの共通接線が引ける。 ※証明は，前問296と同様なので省略する。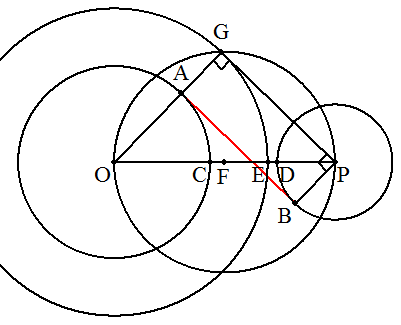

298. 
     

     4個の正三角形の重なった図形Xは，AMに関して対称である。 ABとLKの交点をP，ACとKLの交点をQとすると， △APQは正三角形となる。 DEとBCの交点をR， GHとEFの交点をS， JKとHIの交点をT， ABとFE，IHの交点をそれぞれU，Vとする。 平行四辺形の対辺は等しいから AB＋RE＋SH＋TK＝AP BR＋ES＋HT＋KM＝PM 図形XのAMに関して左側のまわりの長さは， 正三角形APQのAMに関して左側のまわりの長さに等しい。 よって，この図形Xのまわりの長さ6は正三角形APQの まわりの長さに等しい。 AP＝6÷3＝2 AP：AM＝2：√3であるから AM＝√3･･･（答）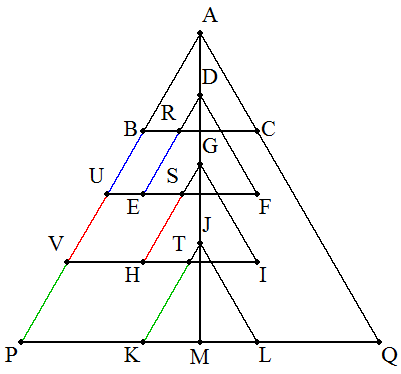

299. 
     

     頂点A，Bから対辺に下ろした垂線の足をそれぞれD，E， ABの中点をF，△ABCの外接円とCGの交点をKとする。 四角形AKBSは平行四辺形となり，FはABの中点であるから， SKの中点でもある。 △SKCにおいて，Jは中線SG，CFの交点であるから重心で， △ABCの重心と一致する。 よって，△ABCの垂心Sと重心Jと外心Gは1直線上にあり， SJ：JG＝2：1である。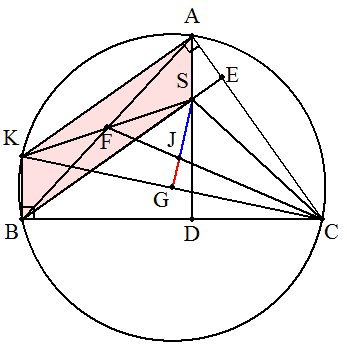

300. 
     

     （作図） 右図のように，BAとCDの交点をE，ADとBCの交点をF， ∠BEC，∠AFBの二等分線と4辺との交点をI，G，H，J とすると，四角形GHIJはひし形となる。 円に内接する四角形ABCDの2組の対辺のなす角 の各二等分線と4辺との交点でできる四角形は ひし形である。 （証明） EGとFJの交点をKとする。 △JBF∽△HDFであるから， ∠EJH＝∠JBF＋∠BFJ＝∠HDF＋∠DFH＝∠EHJ よって△EJHは二等辺三角形となるから， JK＝KH，EK⊥JH･･･① 同様に，△GBE∽△IDEであるから， ∠FGI＝∠GBE＋∠BEG＝∠IDE＋∠DEI＝∠FIG よって△FIGは二等辺三角形となるから， IK＝KG，FK⊥IG･･･② ①，②より四角形GHIJにおいて，対角線が垂直で， 互いに他を二等分しているのでひし形となる。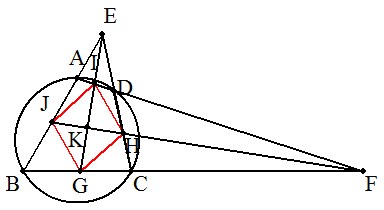