(1)
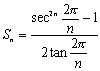
(2) 2π
補足→こちら
(1) 1,2,3
(2) n
(3) π/2
(1)
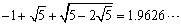
(2) a=1
(3) 1/3,1/3,1/7,1/7
(4) π/4
(5) 1/2
| (1) 1 (2) 1/3 ※y=x+1/3は与えられた曲線の漸近線となる。 | 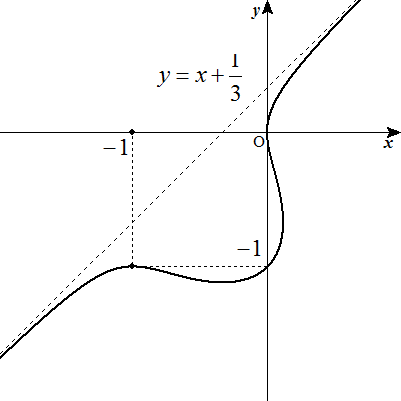 |
1 (
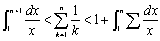 )
)
(1) 1/e
(2) 0
(1) 略
(2)
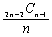
(3) 4
(4) 4
(1)
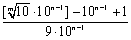
(2)
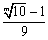
(3) m=26
n(n+1)
(1)
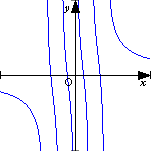
(2)
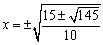
(1)
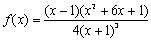
(2)
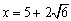 のとき,最大値
のとき,最大値 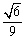
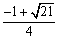
2m+n-1Cn
1/5 (x=y,z=2 のとき)
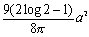
□⇒(x2+y2)2=2a2(x2-y2)
□⇒r2=2a2cos2θ
□=2a2
□=
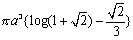
条件
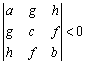
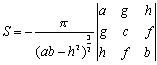
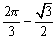
(1)
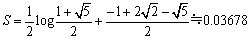
(2)
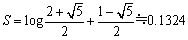
(3)
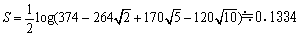
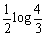
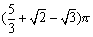
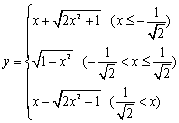
(1) 省略
(2)
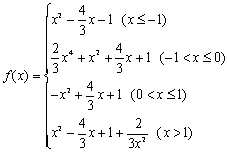
(3) 5/8 (x=-1/2)
(4)107/15
*
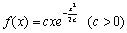
(1)
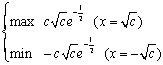
(2) 2c2
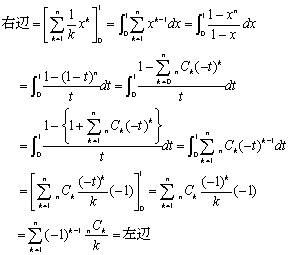
(1)
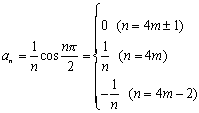 ,
, 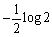
(2)
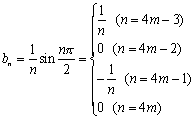 , 3π/4
, 3π/4
(1)
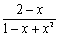
(2)
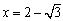 のとき,
のとき,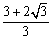
(3)
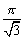
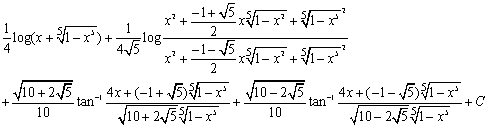
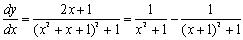 より,
より,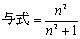
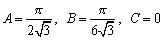
(1)
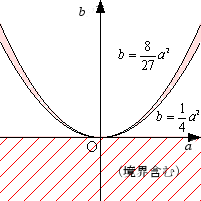
(2)
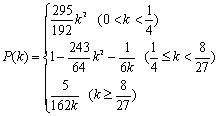
(3)
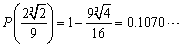
(1)①
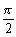 ,1
,1②
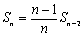
③ π/2
④
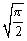
(2)①
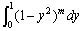
②
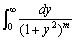
③
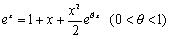 (x=-y2とおく)
(x=-y2とおく)④ ③をm乗して
⑤
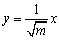 とおく
とおく(3)①
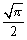
②
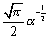
③
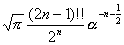 (②の両辺をαでn回微分)
(②の両辺をαでn回微分)④ ③で
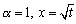 とおく。
とおく。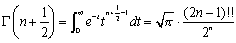 ((-1)!!=1とする)
((-1)!!=1とする)
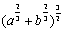
(1)
(2) 9/16
(3) 4/3
(1) 13542/2695(=5.0248608)
(2) ab(a2+ab+b2)(a2+3ab+b2)/{(a+b)2(a+2b)(2a+b)}
(1) (-20+15√2+12√5+11√10)π/40(=4.9347392)
(2) (π/4){(a+b-c)/2}2{√{(c-a)/(2c)}+√{(2c)/(c-a)}+√{(c-b)/(2c)}+√{(2c)/(c-b)}+(3√2-4)/2}
ただし,c=√(a2+b2)
(3) (π/4)r2{sin(A/2)+1/sin(A/2)+sin(B/2)+1/sin(B/2)+sin(C/2)+1/sin(C/2)-2}
ただし,sin(A/2)=√{(1-cosA)/2}=√{(s-b)(s-c)/(bc)}等々,r=√{(s-a)(s-b)(s-c)/s},s=(a+b+c)/2
3545886/737891
⊿GBD内の正方形の面積の和→19200/15059,
⊿FCE内の正方形の面積の和→810/1369,
五角形AGDEF内の正方形の面積の和→144/49
詳しくはこちら(こだわり数学 53.直角三角形に含まれる連結した無限個の正方形の面積和)
15(-18716301655917075+41592656472339421√3)/146108147183519224
解答→こちら
(1170√14+735√26+624√35+504√65-7280)π/1638(=16.49533725)
参考資料→こだわり数学 54.三角形に含まれる連結した無限個の円の面積和(PDF)
π(27π4-2624)/2
=9.496183091
解答→こちら
2πr2h3/{3(4r2+3h2)}
(1) 4a2/9
(2) 3a2/8
(3) 32r2/25
(4) 2{805+328√5-4√(61825+27590√5)}a2/361
(5) 24(13-4√3)a2/121
A問題89を参照のこと。
(1) (71-17√17)/16 (BG=(-3+√17)/4のとき)
(2) {-7+(197-18√113)^(1/3)+(197+18√113)^(1/3)}/6=0.3462719059
(1) (√2-1)a
(2) a(b2+c2-a2)/(2b2)
(3) {-c(2a+c)+c√(8a2+12ac+5c2)}/{2(a+c)}
証明→こちら(こだわり数学 3)
B97参照。Wallisの公式使用(こだわり数学 3)。
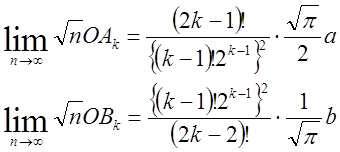
(1) x=-4-√17,-4+√17,4-√15,-4+√19,4-√13,-4+√21,4-√11,-4+√23,1,7
(2) α=(n3+√(n6-4n2-4n-4))/2,β=(-n3-√(n6+4n2-4n-4))/2
(3) -2
2123577π/50960
(≒130.915)
B問題71参照。
2種類の無限等比級数の和となる。
因みに,△ABC=168である。
{2an+1-(a+1)+(-1)n-1(a-1)}/{2(a+1)(a-1)}
∠ABC=π/8のとき
(補足1)(△EBF-△AED)/△ABC=(3-2√2)/2=0.0857865となる。
(補足2)sin2∠ABC=(√5-1)/2のとき,(△EBF-△AED)/△ABC=√(10√5-22)/8=0.0750706である。
(1) A(15/4,0)
(2) AP=BQ=5/4
(補足)「フィロー氏の線」に関する問題