■趣味の数学問題集・Ａ問題の答

  1. △ACE＝b(a+b)/(a-b)

  2. △ABC＝a(2a+b)/2，
    △ABC＝15

  3. △ABC＝3b√(a2-b2)/2

  4. ひもをπ：4に内分するところで切って，πの比の長さで切ったひもで円を，
    残りのひもで正方形を作ったとき，その面積和は最小となる。
    ※解答→こだわり数学20

  5. V＝√ {(p-a2)(p-b2)(p-c2)}/24
    ただし，p=(a2+b2+c2)/2
    ※解答→こだわり数学24

  6. xy=yx
    ※解答→こだわり数学35のNo.5

  7. 735
    解答例→こちら

  8. r1：r2：r3：r4＝1：2：3：4
    解答例→こちら

  9. (1)　39a/320
    　（=0.121875a）
    (2)　3(-56-33√3+16√13+9√39)a/16
    　（=0.138024a）
    解答→こちら

  10. (1)　略（線分比の定理を使うと中学生でも証明できる。）
    (2)　(1)と同様
    (3)　(1)と同様

  11. OA1＝256/77，OB1＝63/32

  12. e=3a/8
    f=a/6
    g=a/16
    h=3a/56
    i=(27-12√2)a/98
    j=(45-24√2)a/194
    k=(7-2√6)a/25
    l=(93-54√3)a/313

  13. 2074
    ※因みに，n=66である。

  14. (n+1)/2

  15. (1)　39(7-3√3)a/1232
    (2)　3(-845-585√3+338√10+156√30)a/2704

  16. （証明）

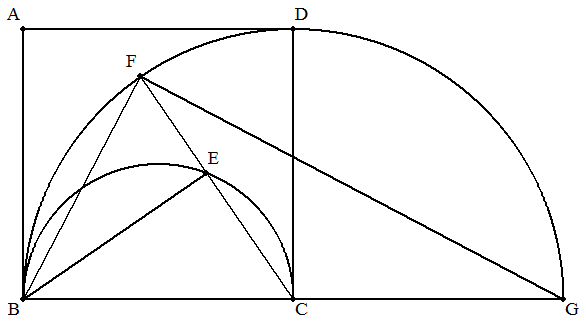
    扇形CBDをCDに関して対称移動し，移動した点Bを点Gとする。
    ∠BFG＝90°，∠BEC＝90°である。
    ∠ABF＝∠FGC＝∠GFC＝90°－∠BFE
    ∠EBF＝180°－（90°＋∠BFE）＝90°－∠BFE
    よって　∠ABF＝∠EBF　（終証）

  17. 正方形の1辺　8
    円の半径　√13

  18. （省略）
    （ヒント）△ABCの内心Iは，△DEFの垂心に一致し，それは△LMNの外心に一致することを示す。

  19. EF＝13√13
    一般に，BC＝a，AC＝bのとき，EF＝(a2/3+b2/3)3/2


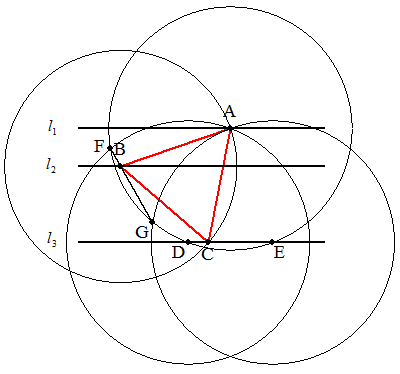
  20. 点Aをl1上に任意にとる。
    点Aを中心としてl3とD，Eで交わる円①を描く。
    点Aを中心として，2点D，Eを同じ方向に60°回転させ，それぞれ点F，Gとする。
    （点Dを中心とする半径DAの円と①の交点がF，点Eを中心とする半径EAの円と①の交点がG）
    FGとl2との交点をB，Aを中心として点Bを逆方向に60°回転させl3上に点Cをとる。
    最後に，AB，BC，CAを引いて，正三角形が作図できる。

  21. (π/2-1)a2

  22. (1)　2a2/(sinα+cosα+1)
    (2)　sinα＝3/5，4/5

  23. (1)　(9√2-6√3+2√6)/6
    (2)　(-9+8√3)/4

  24. (1)　√3a2/6
    (2)　11√3a2/60
    (3)　3√3a2/20
    (4)　2√3a2/15
    ※補足
    　(1)：(2)：(3)：(4)＝10：11：9：8 であるから
    　右の図より，次のことが分かる。
    　(1)＋(2)＋(3)＝(2)×2＋（4）＝(正六角形)/3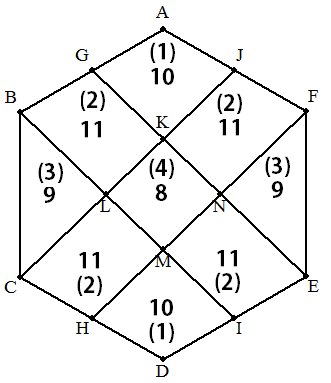


  25. (1)　a2/20
    (2)　3a2/20
    (3)　a2/5

  26. 180°×(n-4)

  27. 180°

  28. 略

  29. 21007i

  30. 略

  31. ABの中点Dを中心に点Aを90°回転させた点をEとする。
    Eを中心とする半径EAの円①を描く。
    点Aを中心に点Cを60°回転させた点をFとする。
    Fを中心とする半径FAの円②を描く。
    このとき，2円①，②の交点のうち，点Aでない方が点Pとなる。
    もう一つの点Qも同様に作図できる。
    （証明）
    円①について，中心角と円周角の関係より
    ∠AEB＝90°であるから，∠APB＝45°となる。
    また，円②についても同様に
    ∠AFC＝60°であるから，∠APC＝30°となる。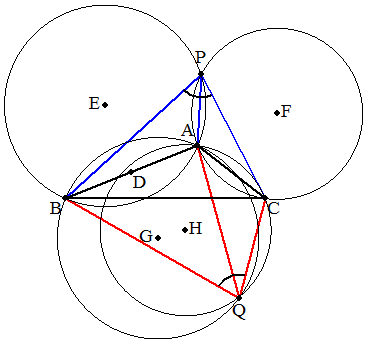

  32. (4+√2)a2/21

  33. 与えられた同心円を外側からC1，C2，C3とする。
    C1上に任意に点Aをとり，AO＝APとなる点Pを円C1上に1つとる。
    点Pを中心に円C3の半径で円弧を描き，円C2との交点を図のようにB，Dとする。
    (1)　点Aを中心にABを半径とする円弧を描き，円C3との交点をCとする。
    （図のように交点は2個あるが，図の方をCとする。）
    このとき，△ABCが正三角形となる。
    (2)　点Aを中心にADを半径とする円弧を描き，円C3との交点をEとする。
    （図のように交点は2個あるが，図の方をEとする。）
    このとき，△ADEが正三角形となる。
    （証明）
    (1)　△AOC≡△APB（3辺相等）であるから，∠PAB＝∠OAC･･･①
    また，点Pのとり方から，△APOは正三角形より　∠PAO＝60°･･･②
    ①，②より　∠BAC＝60°
    AB＝ACより　△ABCは正三角形となる。
    (2)　△AOE≡△APD（3辺相等）であるから，∠PAD＝∠OAE･･･③
    また，点Pとり方から，△APOは正三角形より　∠PAO＝60°･･･④
    ③，④より　∠DAE＝60°
    AD＝AEより　△ADEは正三角形となる。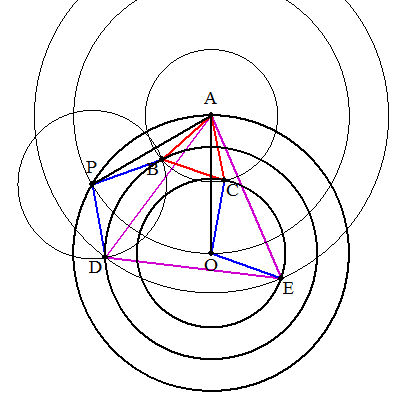

  34. （ア）　(√6-√2)r/2
    （イ）　(√6-√2)r/2
    （ウ）　√{(21-6√3)/37}r

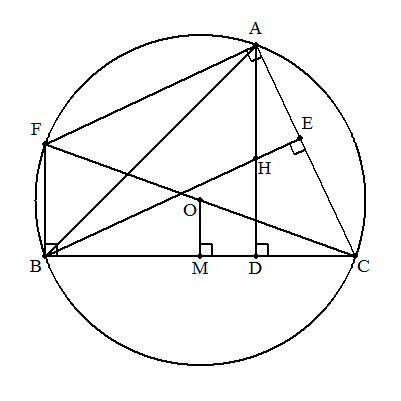
  35. （証） AHとBCとの交点をD，BHとCAとの交点をE，
    COの延長と△ABCの外接円の交点をFとする。
    △CFBにおいて，OはCFの中点，MはCBの中点であるから
    中点連結定理より　2OM＝FB･･･①
    FCは直径であるから，∠FBC＝90°
    また，∠ADC＝90°であるから
    FB∥AH･･･②
    同様に　∠FAC＝90°，∠BEC＝90°より
    FA∥BH･･･③
    ②，③より四角形FBHAは平行四辺形となるから
    FB＝AH･･･④
    ①，④より　AH＝2OM（終証）
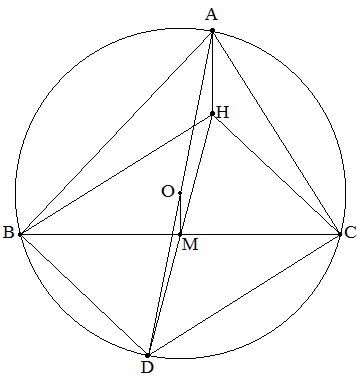
    （別証） AOを延長し，△ABCの外接円との交点をDとすると，
    四角形HBDCは平行四辺形となる。
    （∵BH⊥CA，DC⊥CAよりBH∥DC，同様にCH∥DB）
    よって，DHの中点はMとなる。
    △DHAにおいて，M，OはそれぞれDH，DAの中点である
    から，中点連結定理より，AH＝2OM（終証）

  36. 点Bから直線n，m，l，kに下ろした垂線の足をそれぞれH，I，J，Kとする。
    図のように，点L，Gを，BK上にBL＝HI，LG＝JKとなるようにとる。
    AGと直線kとの交点をC，Cから直線lに下ろした垂線の足をDとし，
    DLと直線mとの交点をE，Eから直線nに下ろした垂線の足をFとする。
    最後に，AC，CD，DE，EF，FBをつなぐと得られる。
    （証明略）
    A問題144の解答を参考にせよ。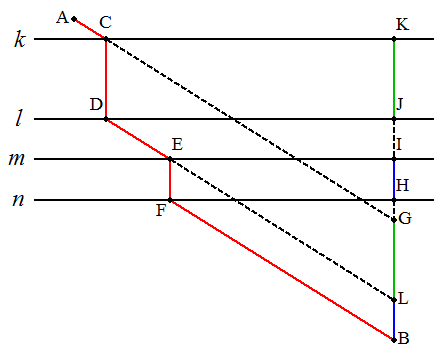

  37. √2 a/√(1/sin2α-2/sin2β+1/sin2γ)
    ※　sinをtanに変えても同じ。

  38. a√(e2-a2)/4

  39. 点GをBの上方に次のようにとる。
    BG⊥n，BGの長さは平行な2直線m，nの距離。
    点HをGの上方に次のようにとる。
    GH⊥l，GHの長さは平行な2直線k，lの距離。
    AHと直線kとの交点をC，Cから直線lに下ろした垂線の足をDとし，
    DGと直線mとの交点をE，Eから直線nに下ろした垂線の足をFとする。
    最後に，AC，CD，DE，EF，FBをつなぐと得られる。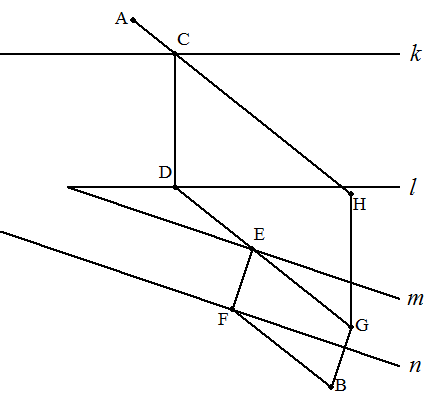

  40. （AからB）
    Bの上方に点Pを，BPが川幅で，BP⊥lとなるようにとる。
    APと川岸kとの交点をDとし，Dから川岸lに下ろした垂線の足をEとする。
    （BからC）
    Cの上方に点Qを，CQが川幅で，CQ⊥nとなるようにとる。
    BQと川岸mとの交点をFとし，Fから川岸nに下ろした垂線の足をGとする。
    （CからA）
    Qの上方に点Rを，QRが川岸k，lの川幅で，QR.⊥lとなるようにとる。
    ARと川岸kとの交点をKとし，Kから川岸lに下ろした垂線の足をJとする。
    あとは，AD，DE，EB，BF，FG，GC，CH，HI，IJ，JK，KAを繋ぐと最短経路が
    得られる。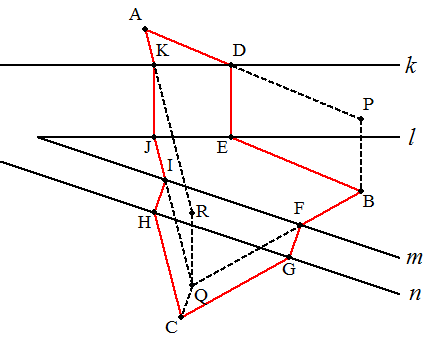

  41. (1)　1/3
    (2)　3-2√2

  42. (11√3+3√11)/2
    Hint：PQ＝2xとおいて，正三角形の高さを方程式で表す。

  43. √3[2a+3b+c+√{(b+c)(4a-3b+c)}]/2

  44. AE＝3
    一般に，BE＝a，EC＝bのとき，AE＝√{a(2b-a)}

  45. （略）

  46. BC=a，△ABCの高さをhとすると，△ABC＝(1/2)ah。
    BQ＝ka（0<k<1）とおくと，
    △PBQ，△RQCの高さはそれぞれkh，(1-k)hとなる。
    平行四辺形APQR
    ＝△ABC－（△PBQ＋△RQC）
    ＝△ABC－{(1/2)ka・kh＋(1/2)(1－k)a・(1－k)h}
    ＝△ABC－(1/2)ah{k2+(1－k)2}
    ＝△ABC－△ABC{2(k－1/2)2＋1/2}
    ＝△ABC｛1/2－2(k－1/2)2｝
    よって，ｋ＝1/2のとき，面積は最大となる。
    このとき，点QはBCの中点である。

  47. 点Aから直線lに下ろした垂線の足をHとする。
    AHの垂直二等分線と円との交点を図のようにB，Dとする。
    題意に適する点はB，Dの2つある。
    （証明）BD∥lであるから
    AB：BC＝AM：MH＝1：1，
    AD：DE＝AM：MH＝1：1　（終証）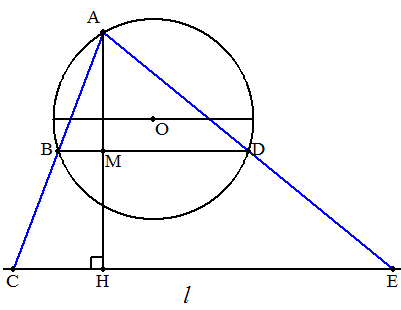

  48. 円Oの半径をrとする。
    点Pを中心，半径2rの円と円Oの交点の一つをCとする。
    COの延長と円との交点をB，PBと円との交点をAとする。
    （証明）
    △PCAと△BCAにおいて　CP＝CB
    BCは直径であるから　∠CAB＝90°
    よって　∠CAP＝90°
    △CBPはCP＝CBの二等辺三角形であるから
    ∠CPA＝∠CBA
    よって　△PCA≡△BCA
    従って　PA＝AB　（終証）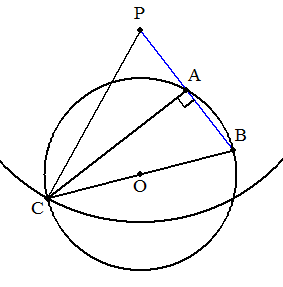

  49. 点Bの点Oに関する対称点をEとする。
    AEの垂直二等分線と円との交点をCとする。
    COの延長と円との交点をDとすれば，AC＝BDとなる。
    （証明）点Bの点Oに関する対称点をEとすると
    BO＝EO，OD＝OC，∠BOD＝∠EOCより
    △OBD≡△OEC
    よって　BD＝EC･･･①
    ABの中点をM，ABの垂直二等分線と円との交点をCとすると，
    △CEM≡△CAMより　EC＝AC･･･②
    ①，②より　AC＝BD　（終証）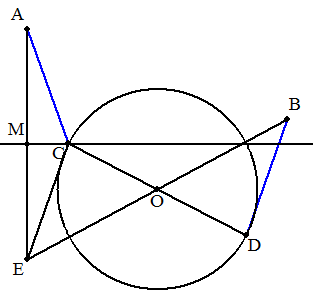

  50. PHと直線lとの交点をQとする。
    Hを中心，半径QHの円に点Pから図のように接線を引き，
    直線l，mとの交点をそれぞれA，Bとし，PBを結ぶとよい。
    （証明）
    △BHAにおいて，∠BHA＝∠QAH（錯角）･･･①
    ∠BAH＝∠QAH･･･②
    （∵AHは∠QABの二等分線であるから）
    ①，②より　∠BHA＝∠BAH
    よって　△BHAは二等辺三角形であるから
    AB＝BH　（終証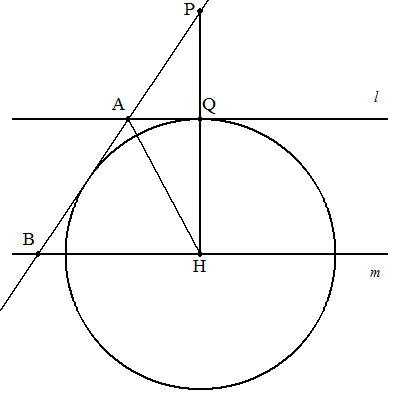）