■趣味の数学問題集・Ａ問題の答

  1. (1)　証明
    (2)　証明

  2. (1)　S/2
    (∵)　四角形ABMD＝△ABM＋△ADM＝△ABC/2＋△ADC/2＝S/2
    (2)　S/4
    (∵)　四角形ALMD＝△ALD＋△MLD＝△ABD/2＋△MBD/2＝四角形ABMD/2＝S/4
    (3)　S/4
    (∵)　ADの中点をGとすると，
    　△LME＝△GLM＋△GME＋△GEL＝△GLM＋△GMD＋△GAL（等積変形）
    　＝四角形ALMD＝S/4
    (4)　S/4
    (∵)　(3)と同様
    (5)　△LFEにおいて，△LME＝△LMFであるから，
    　LMとEFの交点はEFの中点Nとなるので，
    　3点L，M，Nは同一直線上にある。
    　※この直線をニュートン線という。

  3. 10：3
    一般に，AB＝a，BC＝b，CD＝c，DA＝dのとき，
    FH：HG＝ac(b2-d2)：bd(c2-a2)

  4. (1)　r＝(-1-2√2+√3+√6)/4（＝0.0882784）
    (2)　順に，r，√2r，√3r，(√6+√2)r/2，2r
    (3)　△CFI⇒[9-7√2+√{3(57-40√2)}]/2（＝0.119105）
    　△AFD⇒(3+√2-√3-√6)/2（＝0.116337）
    　△GHI⇒(9√2-5√6)/4（＝0.120118）
    (4)　順に，3(7-4√3)（＝0.21539），3(3-√3)/16（＝0.23774）

  5. 順に，r/2，r/3，r/4，r/6，r/6，r/6

  6. 証明略
    （ヒント：BE⊥FG，△PBOは直角二等辺三角形）

  7. 4：5：3

  8. 証明→こちら

  9. (1)　a：c　（点Eは△FBDの傍心となるので，BEは∠Bの2等分線）
    (2)　b2：(ac-b2+c2)　（△AEF∽△ABC）
    (3)　c(a2+b2-c2)：ab2
    (4)　ab√{ac(a+b-c)(-a+b+c)}/{(a+c)(ac+b2-c2)}

  10. (1)　75°
    (2)　m＝11，n＝9
    解答→こちら

  11. （証明）
    ∠AEB＝90°･･･①である。
    （∵）△ADEにおいて，∠ADE＝∠ACB＝60°，AD：DE＝2：1より。
    ∠AFB＝90°･･･②である。
    （∵）AFは正三角形の中線となる。
    ①，②より，4点A，B，F，EはABを直径とする同一円周上にある。
    よって，円周角の定理より，
    ∠BEF＝∠BAF＝∠BAC/2＝60°/2＝30°（終証）
    （補足）
    点DがCからAまで動くと，点EはABを直径とする円の弧AF上を，FからAまで動く。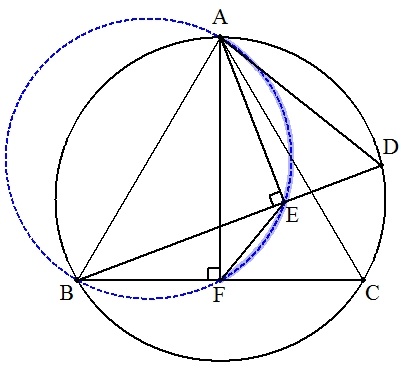

  12. (1)　40°
    （解説）
    　∠OEB＝90°，∠OGB＝90°より
    　円周角の定理の逆より
    　4点O，E，G，Bは同一円周上にある。
    　よって，∠CBE＝∠GBE＝∠GOE（円周角）＝40°
    (2)
    （証明）
    　△OHBと線分BCについて，∠BOH＝∠HBC＝40°
    　線分BCは，△OHBの外接円の接線で，点Bは接点となる。
    （接弦定理の逆）
    　よって，方べきの定理より，CH×CO＝CB2
    (3)　y2=1-1/x
    （解説）
    　(2)より，CH×2＝(2y)2
    　∴　CH＝2y2
    　△HOE∽△COFより
    　OH：OC＝OE：OF
    　ここで，OH＝OC－CH＝2－2y2，
    　OC＝2，OE＝1，OF＝xであるから
    　(2－2y2)：2＝1：x
    　x(2－2y2)＝2
    　よって，y2=1-1/x･･･①
    (4)　x3-3x-1=0
    （解説）
    　直角三角形COFに三平方の定理を適用すると
    　x2+y2=22
    　これに，①を代入すると
    　x2+1-1/x=4
    よって，x3-3x-1=0
    （補足）
    この方程式を角の三等分方程式という。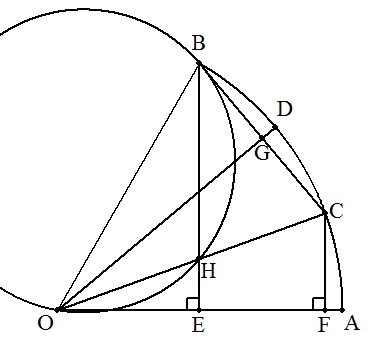

  13. 　SBE
    (1)12√3
    (2)563√14/2
    (3)130/7√910/13
    (4)40√10/2

  14. 　SBE
    (1)a+√(a2+4ab-4b2)2b/√{a+√(a2+4ab-4b2)}
    (2)2a+c{a±√(a2-2ac-c2)}/√(2a+c)
    (3)2b(2b+c)/(2b-c)√[{2b(2b-c)/(2b+c)}]
    (4)b+d+√(b2+6bd+d2)2b/√{b+d+√(b2+6bd+d2)}

  15. (1)　6
    （補足）BE＝a，△AEF＝sのとき，AB＝xとおくと，xは，x3+(a2-2s)x-2as=0の解。
    　 (2)　4√5
    （補足）BE＝a，△DAF＝sのとき，AB＝xとおくと，xは，x3-ax2-2sx-2as=0の解。
    (3)　{a2+s+√(a4+6a2s+s2)}/(2a)

  16. (1)　45°
    (2)　72°
    (3)　36°
    (3)　30°

  17. r1={-2-√2+2√(2+√2)}r/2
    r2={-2+√2+√(4-2√2)}r/2
    r3={-2+√(4+2√2)}r/2

  18. r=ab/{(2n-1)(a+b)+√(a2+b2)}
    解答→こちら

  19. （解答例）
    2014＝1234－5＋6！－7＋8×9
    2014＝123＋45－6！－7－8－√9
    2014＝(－1＋2＋3＋4＋5×6)×(7×8－√9）
    2014＝1×2×(3＋√4×5＋6)×(7×8－√9)

  20. 証明→こちら

  21. （解）
    図のように5つの線分AO1，BO1，O1On，COn，
    AOnで△ABCを4つに分割して面積を考える。
    求めるn個の等円の半径をxとおき，
    △ABCの面積をS，△ABCの内接円の半径を
    r，s＝(a+b+c)/2とおくと，S＝rsとなる。
    BC＝aを底辺としたときの高さをhとおくと，
    S＝ah/2よりh＝2S/a＝2rs/aである。
    S＝△O1AB＋△OnCA＋△AO1On＋台形O1BCOn
    rs＝cx/2+bx/2+2x(n-1)(h-x)/2+{2x(n-1)+a}x/2
    　＝(a+b+c)x/2+(n-1)xh
    　＝sx+(n-1)x×2rs/a
    ∴x＝ar/{a+2(n-1)r}･･･（答）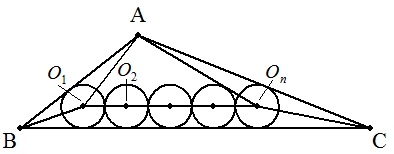

  22. (1)　順に，a2＋b2，b2，a2＋4b2，4a2＋b2
    (2)　a2＋b2
    　※正方形DEFG＝△GLMとなる。
    (3)　√(5a2－6ab＋5b2)

  23. (1)　11
    (2)　√{(l+m+n)2-4ln}

  24. (1)　2√3
    　173(2)を使うと，△AEF＝√{(2+2+3)2-4×2×3}＝5となる。
    (2)　(5√3－5√6＋√15＋√30)/6

  25. (1)　hij/(hi+ij+jh)
    (2)　h2i2j2/√{2h2i2j2(h2＋i2＋j2)－(h4i4＋i4j4＋j4h4)}
    (3)　半径 360/121，面積 129600/(77√1271)

  26. （証明）
    点Gを，FDの延長上にFD＝DGとなるようにとる。
    四角形FBGCは対角線が互いに他を2等分するので，平行四辺形である。
    ∴　中線CF＝GB
    △BCAで中点連結定理より，FD∥AC，FD＝AC/2
    したがって　DG∥AE，DG＝AEより四角形ADGEは1組の対辺が平行で等しいので平行四辺形である。
    ∴　中線AD＝EG
    ゆえに　△BGEは3つの中線を3辺とする三角形である。
    D，E，FはBC，CA，ABの各中点であるから
    △AFE≡△FBD≡△DEF≡△EDC＝△ABC/4
    DはFGの中点であるから
    △DGE＝△DEF＝△ABC/4
    △DBG＝△FBD＝△ABC/4
    また，FE∥BCであるから
    △DEB＝△FBD＝△ABC/4
    よって
    △BGE＝△DGE＋△DBG＋△DEB
    　　　＝(△ABC/4)×3
    　　　＝(3/4)△ABC
    （終証）
    別証明→こちら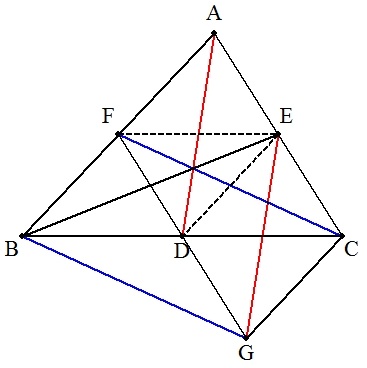

  27. (1)　60
    　（ヒント）メネラウスの定理
    (2)　S2(S1+S2)(S1+S2+S3)/{S2(S1+S2)-S1S3}

  28. (1)　{4a+b-2√(3a2+2ab)}/2
    (2)　（例）
    abr
    8135/2
    9115/2
    183713/2
    254717/2
    323317/2
    327325/2
    497129/2
    506929/2
    569135/2

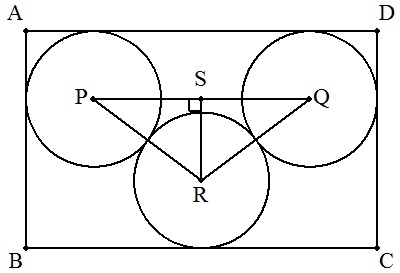    RからPQに下ろした垂線の足をSとする。
    PS＝b/2-r，PR＝2rより　RS＝√{(2r)2－(b/2-r)2}＝a－2r
    r＜a/2に注意してrについて解くと，(1)の結果が得られる。

  29. a=2√{(7-4√2)/17}r
    　=0.9907303159r

  30. a=(√21/7)r
    　=0.6546536707r

  31. a=(1/2)√{(70-22√5)/31)}r
    　=0.4096271367r

  32. a=2√{(17-8√3)/97)}r
    　=0.3600454461r

  33. a=2rsin(π/7)/√{5+4cos(π/7)}
    　=0.2958396036r

  34. (1)　4(2-√3)
    (2)　3(√3-1)/2
    (3)　{-14-10√5+√(1570+698√5)}/19
    　（＝1.031192263）

  35. a＝{2(√5-1)/√105}r
    b＝{4/√35}r
    c＝{2(√5+1)/√105}r
    解答→こちら

  36. EF＝3√3/2
    一般に，AB＝a，AD＝bのとき，
    EF＝(√(4a2-3b2)-b)√3/4
    （Hint）161番より，∠BEF＝30°を利用する。

  37. a2+b2+c2-ab-bc-ca
    （A問題56参照）

  38. 証明→こちら

  39. cx3+(ac+b)x2+(ab+bc+a-3c)x+(a-c)2+(b-1)2=0

  40. 略
    α2+β2+γ2=-2p，α3+β3+γ3=-3q，α4+β4+γ4=2p2，α5+β5+γ5=5pq，α7+β7+γ7=-7p2qを使う。

  41. (1)　14√3+6√15
    (2)　4
    解答→こちら

  42. (1)　(ar+b√(a2+b2-r2))x+(br-a√(a2+b2-r2))y=(a2+b2)r
    　　　(ar-b√(a2+b2-r2))x+(br+a√(a2+b2-r2))y=(a2+b2)r
    (2)　△PQR＝{r(a2+b2-r2)√(a2+b2-r2)}/(a2+b2)
    (3)　ax+by=r2
    解答→こちら

  43. 3√35，[b+√{b(a+b)}]2√{(a+b)(4a+3b)}/(2a)
    解答→こちら

  44. (1)　5/2，[(2a+b)√{a(5a+4b)}-a(4a+5b)]/(2a)
    (2)　3(√29-4)

  45. 証明略

  46. (1)　s/16
    (2)　41s/560
    (3)　23s/168
    ※(3)はA問題65番を参照せよ。
    　一般解→こちら

  47. 1/5

  48. x=2-a-b-c，
    x=4/5

  49. (1)　5:12
    (2)　12
    ※補足　BF＝aのとき，四角形AFED＝3a2/4

  50. 証明略
    （Hint）BAとCDの交点をFとする。
    △ABE∽△DCE
    △BFD≡△BCD
    △ABE≡△ACF
    △ACFの外接円はCFを直径とする円
    これらから証明される。