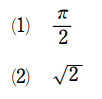1:√2
解答例→こちら
順に,1:√2,8:27
順に,1:2√2,1:2
|
(1) (√2-1)AD (2) (作図例) BDの中点をM,BDの垂直二等分線上に点Eを ME=MDとなるようにとる。 BD上に点QをDE=DQとなるようにとる。 AQとBCとの交点をPとすればよい。 (別法) ADを1辺とする正方形の対角線の1つをAEとする。 AE上に点FをAD=AFとなるようにとる。 点PをBC上にFE=BPとなるようにとる。 | 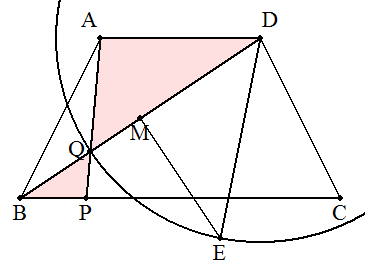 |
|
(1) (√2-1)AD (解答) 便宜上,AB=a,AD=b,CE=xとおく。 △EFC∽△EABより FC:a=x:(b+x) FC=ax/(x+b) DF=a-FC=ab/(x+b) △AFD+△EFC =(1/2)b×ab/(x+b)+(1/2)x×ax/(x+b) =(a/2)(x2+b2)/(x+b) (※) =(a/2){x+b+2b2/(x+b)ー2b} ≧(a/2)[2√{(x+b)×2b2/(x+b)}-2b] =(√2-1)ab 等号は,x+b=2b2/(x+b) すなわち,x=(√2-1)bのとき, 面積和は最小値(√2-1)abとなる。 (※)ここで,xで微分して最小値を与えるxの値を求める 方法もあるが,ここでは,相加平均≧相乗平均を使った。 (2) (作図) DCの延長上に点Gを,CB=CGとなるようにとる。 BCの延長上に点Eを,BG=BEとなるようにとる。 (証明) △CBGは直角二等辺三角形であるから, BE=BG=√2×BC=BC+CEより CE=(√2-1)BC=(√2-1)AD よって 点Eは条件を満たす。 | 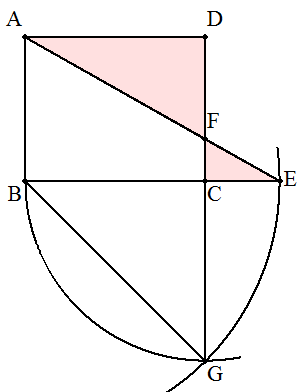 |
(1) S=(1/4)|(a3-1)3/a3(a3+1)|
→A問題314参照
(2) 0<S<3√3/2のとき,2個
S=3√3/2のとき,4個
3√3/2<Sのとき,6個
(3) (2)より,S=3√3/2のとき4個
このとき,a=-(2±√3)(1/3),(7±4√3)(1/3)
(1) (22n-2nCn)/22n+1
(2) 1/√π(≒0.5641895835)
解答→こちら
(1) 3
(2) (1+√5)/2
解答→こちら
a+b
(解)P(acosθ,bsinθ)における接線の方程式は,(cosθ/a)x+(sinθ/b)y=1であるから
A(a/cosθ,0),B(0,b/cosθ)より,AB2=a2/cos2θ+b2/sin2θ=f(θ)とおく。
f′(θ)=0より tanθ=√(b/a)
このθの値に対して,f″(θ)>0であるから,f(θ)は極小かつ最小となる。
最小値は,AB=a+b
解答例→こちら
h=-bg/fのとき,mの最大値は c-f2/b
a1/m-b1/n
解答例→こちら
解答例→こちら
略
解答例→こちら
解答例→こちら
解答例→こちら
解答例→こちら
(1) (x2+y2)2=a2x2+b2y2
(2) (a2+b2)π/2
(1) (x2+y2)2=a2x2-b2y2
(2) (a2-b2)π/2
1
ちなみに,小数第1010位は3,小数第1012位は6
(1) d1={√(2b2+2c2-a2)}/2,d2={√(2c2+2a2-b2)}/2,d3={√(2a2+2b2-c2)}/2
(2) 2d1 (3) 4a
(4) 10d1 (5) 19a
(6) 48d1 (7) 91a
(8) 230d1 (9) 430a
(-11+5√5)/2
AE:EB=x:(1-x)とおくと,x=(-1+√5)/2のとき,最大となる。
背理法を使う。
eを有理数と仮定して,e=m/n(m,nは正の整数)とおく。
n!e=(n-1)!mは正の整数である。
一方,n!e=(n!+n!/1!+n!/2!+…+n!/n!)+{n!/(n+1)!+n!/(n+2)!+n!/(n+3)!+…}
について,左辺と( )の中は正の整数であるから,
R=n!/(n+1)!+n!/(n+2)!+n!/(n+3)!+…も正の整数である。
R=1/(n+1)+1/(n+1)(n+2)+1/(n+1)(n+2)(n+3)+…
<1/(n+1)+1/(n+1)2+1/(n+1)3+…
={1/(n+1)}/{1-1/(n+1)}(無限等比級数の和)
=1/n≦1より,Rは1より小さい正の整数となるが,これは不合理である。
よって,eは有理数でないので,無理数である。
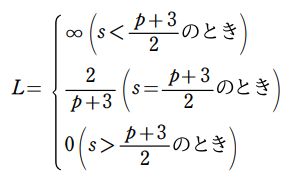
3-e

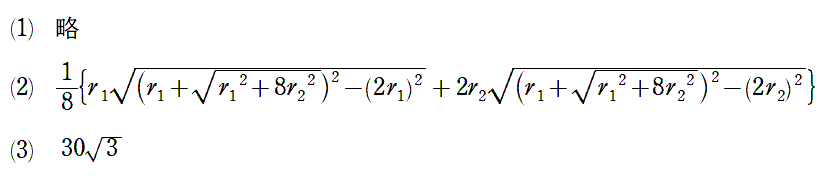
2021
-1
n=6
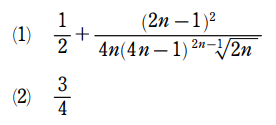
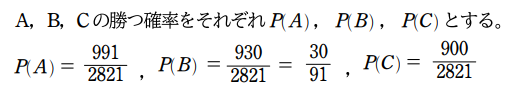
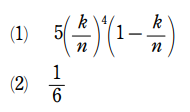
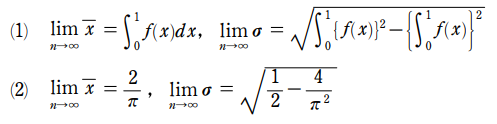
略