■趣味の数学問題集・Ａ問題の答
  1. (1) 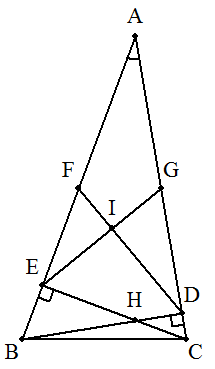BDとCE，DFとEGとの交点をそれぞれH，Iとする。
    四角形ADHEは円に内接するから，
    ∠DHE＝180°－∠EAD＝150°
    △BDF，△CEGは正三角形であるから，
    ∠IDH＝∠HEI＝60°
    四角形IDHEについて，
    ∠EID＝360°－(150°＋60°＋60°)＝90°
    よって，DF⊥EG
    (2)(1/8)bc

  2. （証明）
    線分AQについて，∠APQ＝∠ACQであるから
    円周角の定理の逆より，
    4点A，P，C，Qは同一円周上にあるから，
    ∠QAC＝∠QPC
    よって，∠DAB＝∠BPEよりBD＝BE
    従って，△BDEは二等辺三角形である。（終証）

  3. 略証
    (1)△ABE≡△ADFより，△AEFが直角二等辺三角形となり示される。
    (2)∠AEF=∠ACF=45°より，四角形AECFは円に内接する。
    △AEFは直角二等辺三角形となるから，△ABE≡△ADFとなり示される。

  4. (1)　1/18
    (2)　EF：FD：DE＝√19：√13：2√7

  5. 2r1r2√(r1r2)/(r1-r2)

  6. r1r2(tanα-tanβ)
    ただし，tanα＝√{d2-(r1-r2)2}/(r1-r2)，tanβ＝√{d2-(r1+r2)2}/(r1+r2)
    α＝∠ABD，β＝∠CBD

  7. 3θ/4－π/8（≒0.3027723）
    ただし，θはsinθ＝4/5を満たす角（ラジアン）である。
    解答例→こちら

  8. √7/8－θ/8（≒0.146381）
    ただし，θはcosθ＝393/4096を満たす角（ラジアン）である。
    解答例→こちら


  9. (1)　20°
    ∠BAC=2∠BDCより，3点B，C，Dは点Aを中心とする円周上の点
    (2)　34°
    ∠ADC（優角）＝2∠ABC（劣角）より，3点A，B，Cは点Dを中心とする円周上の点

  10. 60°－α

    解答→こちら

  11. 1/(2n-1)

  12. AB=√3(p+q)+√(3p2-2pq+3q2)
    AB=8√3

  13. BE=xとおくと，4x3-x2+2x-1=0
    これを解いて，BE=(1/12){1+(181-24√78)1/3+(181+24√78)1/3}(=0.432041)

  14. {9-7√2+√(740-466√2)}/34
    （近似値　0.238212）

  15. π/3-(-2+2√3+√7)/8+(1/4)Arcsin{(1+√7)/4}-Arcsin{(5-√7)/8}
    （近似値　0.521454）

  16. (1)a3-12a2+34a-24=0
    （近似値）a=8.21819
    (2)3r3-10r2+3r+8=0
    （近似値）r=2.51327


  17. 略
    Hint　A115(6)
    解答→こちら

  18. 13/90
    （補足）AE=aのとき，S=a(1-a)(1+2a-2a2)/{(2-a)(1+a)}

  19. 円P(p)，Q(q)の半径は，p=(3-√5)/4，q=√5/10
    （補足）AE=aのとき，p=(1+a-√(1+a2)/2，q=a{(1+a)√(2-2a+a2)-a√(1+a2)}/{2(1+a-a2)}

  20. 49√3/100

  21. {π(a2+c2)(b2+c2)-4c(b-a)(ab-c2)}/(8c2)
    解答→こちら

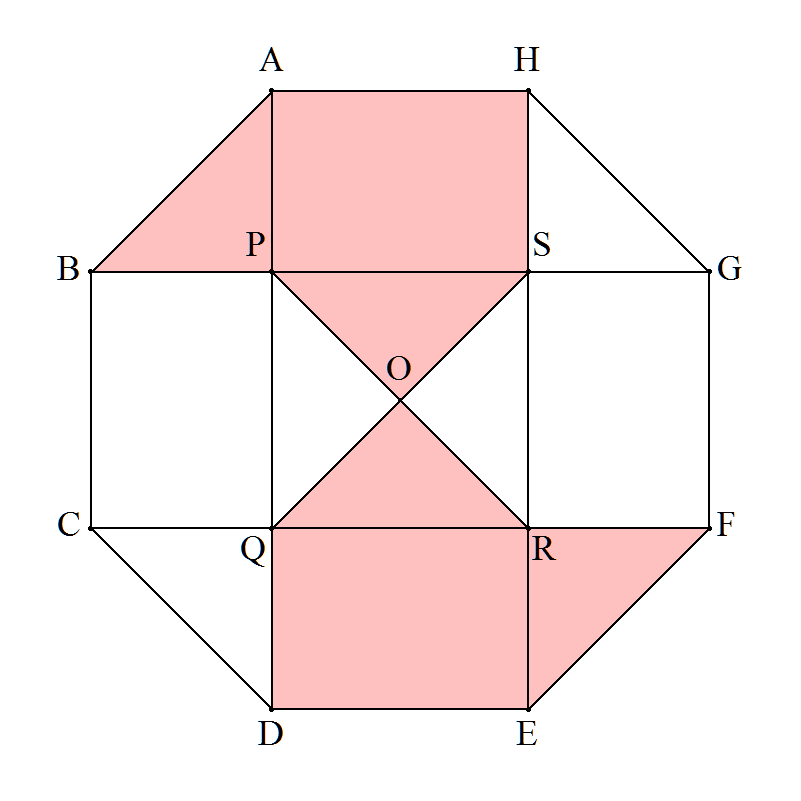
  22. (1) 図のように補助線を引き，記号をつける。
    △HSG≡△POSであるから
    台形ABGH＝六角形OSHABP
    正八角形は合同なこの六角形4個に分割できる。
    よって，（正八角形の面積）：（台形ABGH）＝4：1　（終証）
    (2)証明→こちら
    (3)略

  23. Hint：前問(2)
    証明→こちら

  24. (43-24√3)/6


  25. (1)　b=13
    (2)　b=√{(a3-a2c+ac2+c3-ab2-b2c)/(a+c)}

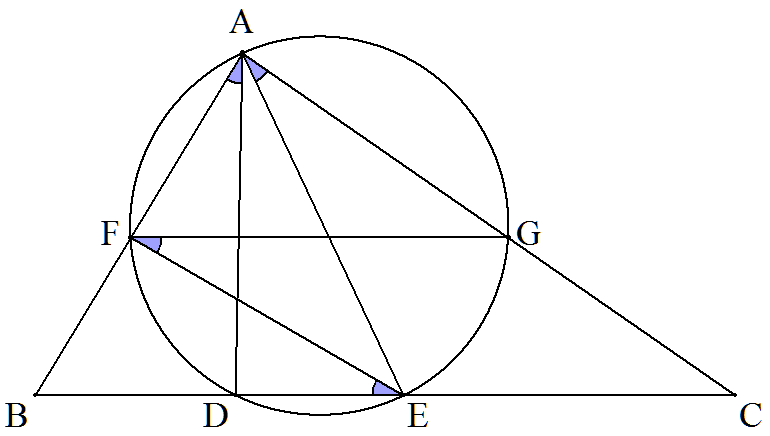
  26. ∠GFE＝∠GAF(円周角)
    　　 ＝∠FAD（仮定）
    　　 ＝∠FED(円周角)
    ∠GFE=∠FED(錯角)より，FG∥DE
    よって，FG∥BC

  27. 略
  28. 略

  29. 両辺別々に展開すると，ともに
    216a6-432a5b+720a4b2-640a3b3+480a2b4-192ab5+64b6
    となる。


  30. (1)　(a+b+c)(a2+b2+c2)/(4abc)
    (2)　(1)と同じ

  31. 解答例→こちら




  33. 1/4
    ※BC，CA，ABの値に関係なく，1/4となる。
    （略解）∠HBL＝∠HAM＝∠DBLより△HBL≡△DBL　∴HL＝DL
    よって，L，M，NはそれぞれHD，HE，HFの中点
    中点連結定理より　△LMN∽△DEF
    相似比1：2であるから面積比1：4
    従って，結論が得られる。

  34. 証明例→こちら

  35. (1)　x5-4x4+6x3-4x2+x-1=0
    (2)　x4-6x3+12x2-8x-1=0

  36. (1)　略
    (2)　略

  37. 47
    （補足）5m+13nの形に表すことができない整数は
    1，2，3，4，6，7，8，9，11，12，14，16，17，19，21，22，24，27，29，32，34，37，42，47の24通り

  38. 解答例→こちら

  39. (1)　略
    (2)　外心
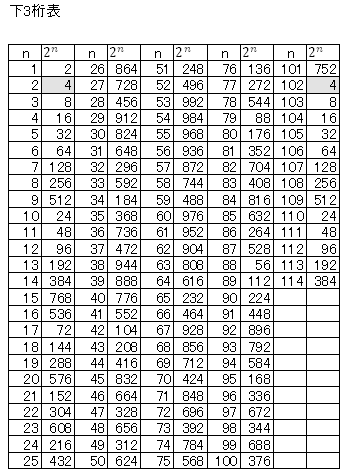
  40. 右の下3桁の表より2102の下3桁が004となり，22と同じになる。
    2018=1+100×20+17
    よって，144となる。
    （補足）22018=30097…742144の608桁


  41. 証明例→こちら



  42. 99999999992=(1010-1)2=1020-2・1010+1=1010(1010-2)+1
    10000000000・9999999998+1=99999999980000000001…（答）


  43. (1)　(185√2-145√3-133√5+135√7+62√30-50√42-34√70+22√105)/215
    =0.12456272786101643477…
    (2)　(7534√2＋4883√3－5231√5＋7399√7－1061√11－3863√30＋1823√42ー533√66ー611√70－583√105＋1233√110－1577√154＋1105√165－1183√231＋73√385＋294√2310)/43684
    =0.088146822327578890056…


  44. 証明例→こちら



  45. 証明例→こちら



  46. 解答例→こちら



  47. 解答例→こちら



  48. 解答例→こちら



  49. 解答例→こちら



  50. 解答例→こちら