(1) b√(a2+k2b2)/a
類題の解答→こちら
(2) b{√(b2+ab)-√(b2-ab)}/a
(例)
| AB | BC | FD |
| 96 | 100 | 125 |
| 1440 | 2028 | 2197 |
| 3600 | 4335 | 4913 |
| 8064 | 5000 | 15625 |
| 17640 | 17661 | 24389 |
| 28800 | 67240 | 68921 |
| 29400 | 47915 | 50653 |
(1) a2/√{a2+(a-b)2}
(2)
| BC | CA | BD |
| 20 | 5 | 16 |
| 156 | 91 | 144 |
| 255 | 119 | 225 |
| 609 | 29 | 441 |
| 600 | 425 | 576 |
| 1295 | 851 | 1225 |
| 1640 | 1271 | 1600 |
| 2385 | 901 | 2025 |
(1) x=z2/y+y-z
(2) r=xy/(x+y)
※1/r=1/x+1/y
→円に台形が外接している。円の半径の逆数は,台形の平行な2辺の逆数の和に等しい。
| (1) | (a+b)/b 回転 (具体例) a=3,b=2のとき,2.5回転 | 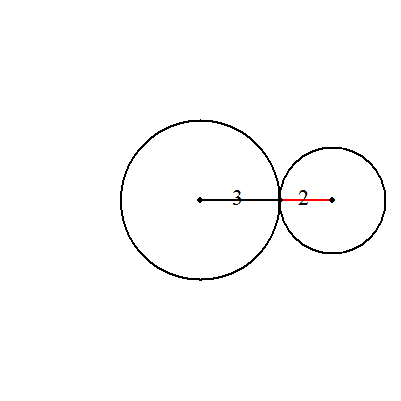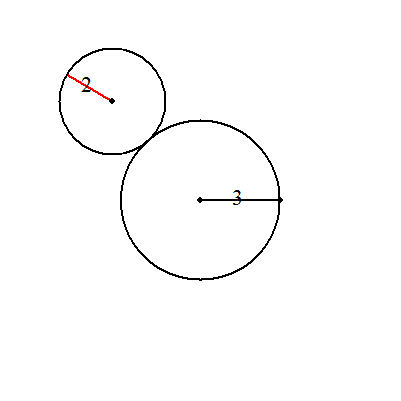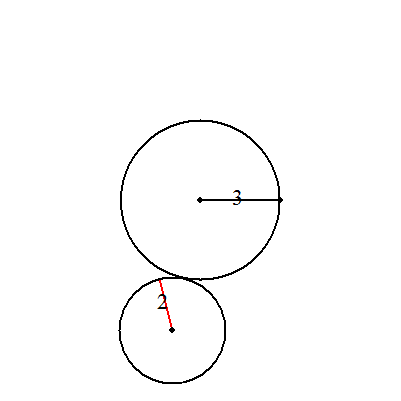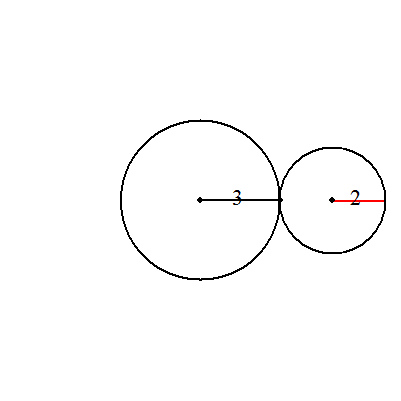 |
| (2) | (a-b)/b 回転 (具体例) a=7,b=2のとき,2.5回転 | 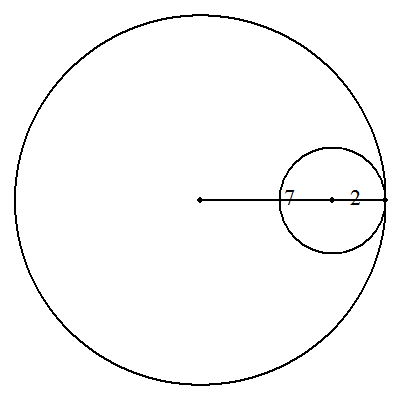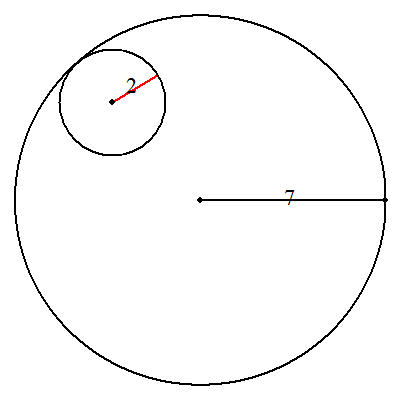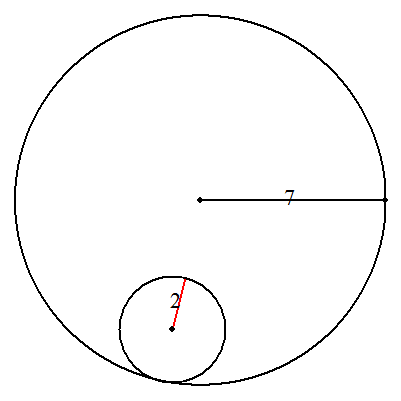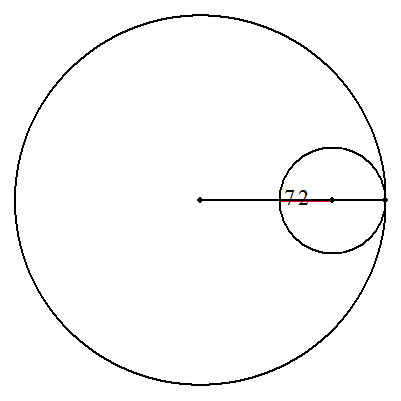 |
(280×15÷24+5)×25÷12.85=?
180°/7
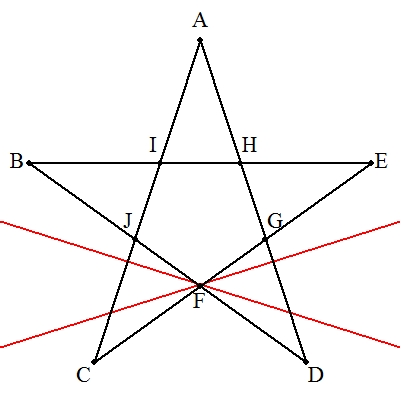
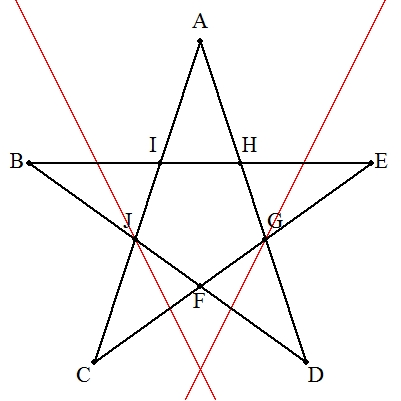
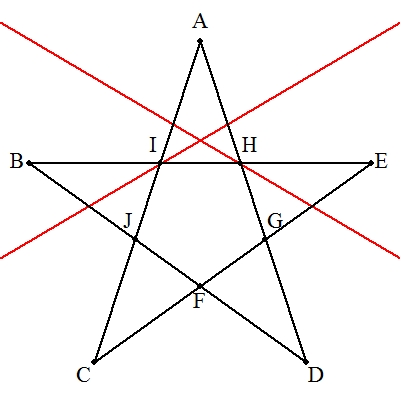
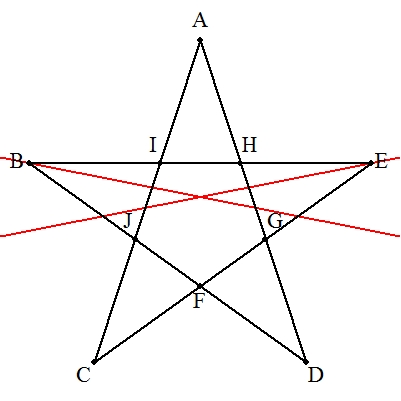
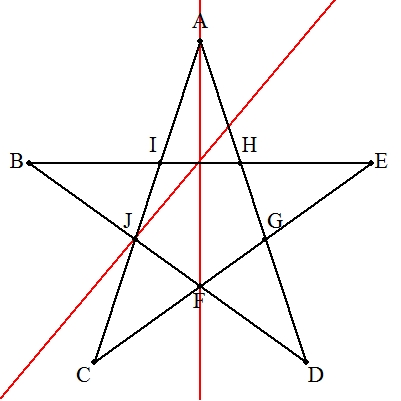
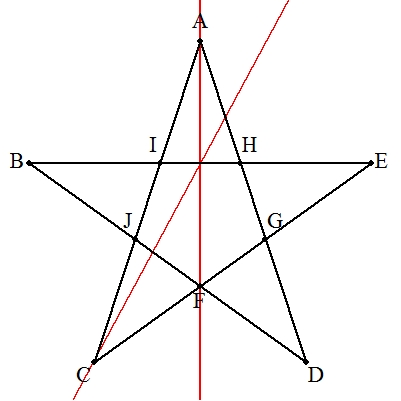
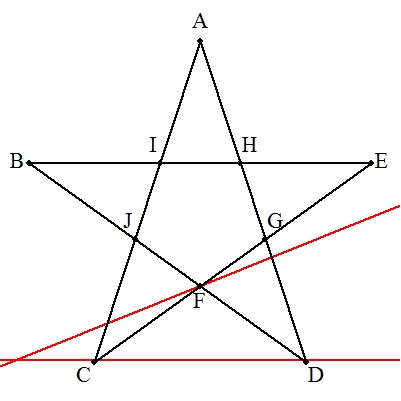
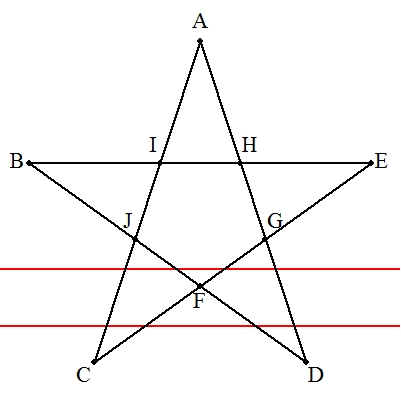
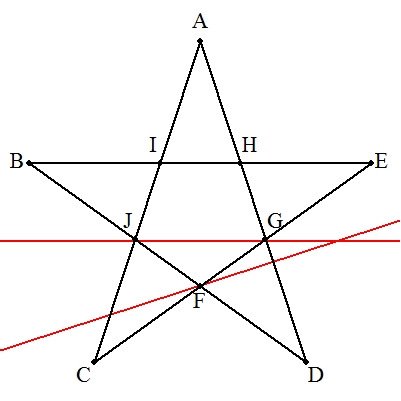
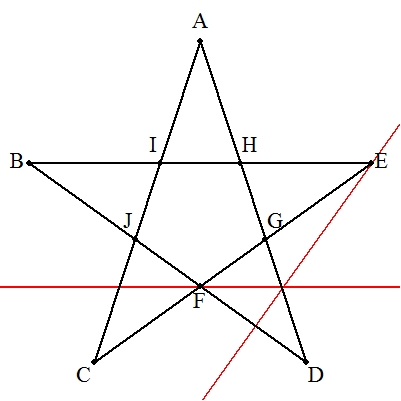
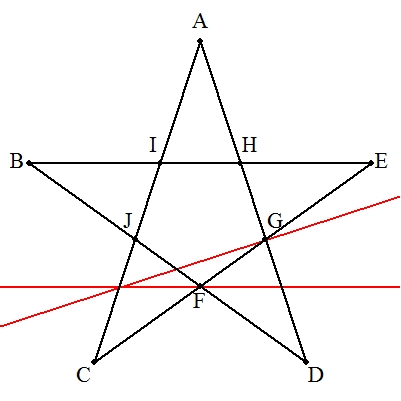
| デザルグの定理を利用すればよい。 右の手順で作図する。 解説→こちら |  |
| (1) | 四角形ABDGにトレミーの定理を適用すると, ac+ab=bc よって,1/b+1/c=1/a |
| (2) | 略 (四角形ABCGとACDGにトレミーの定理を適用し,cを消去する。) |
| (3) | y3-2y2-y+1=0 |
| (4) | z3+z2-2z-1=0 |
| (5) | 5 解答例→こちら |
| (6) | 6 解答例→こちら |
解答例
| (1) | 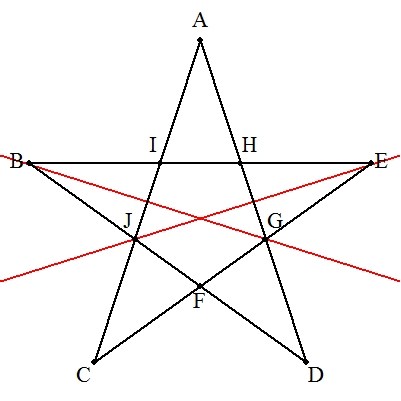 |
 |
 |
 |
 |
 |
|
 |
 |
 |
|
 |
 |
 |
| (2) | 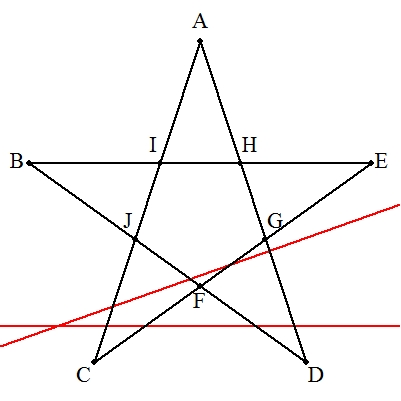 |
r=4R/13
(1) 証明→こちら
(2) r=(5√2-1)a/49
(証)DE=a(一定),AC=b,CB=c,斜線部分の面積をSとおくと,
S=π((b+c)/2)2-π(b/2)2-π(c/2)2
=πbc/2
方べきの定理より AC・BC=DC・ECであるから (※)
bc=(a/2)2
よって S=πa2/8(一定)となる。(終証)
(※)方べきの定理を使わない場合
△BCD∽△DCAより
c:a/2=a/2:b
bc=(a/2)2
(1) 略
(2) 略
(3) 略
証明→こちら
(1) 証明
(2) 証明
(3) 証明
(4) 証明
(5) 証明
(6) 証明
(1) ① ab/(2a-b),② 15
(2) ① (a+b+√(a2+6ab+b2))/2,② 20
(3) ① (b+√(b2+4ab-4a2))/2,② 6
(4) ① (a+b+√(a2+b2))/2,② 35
(5) ① ab/√(2a2-2√2ab+2b2),② 28/5
(補足)
正方形の一辺ABが有理数になる例
| a | b | AB |
| 4√2 | 7 | 28/5 |
| 12√2 | 17 | 204/13 |
| 15√2 | 23 | 345/17 |
| 24√2 | 31 | 744/25 |
| 21√2 | 41 | 861/29 |
| 35√2 | 47 | 1645/37 |
| 40√2 | 49 | 1960/41 |
(補足)
BE=a,AF=b,AB=xとおくと,
xは4次方程式 2x4+(2a2-b2)x2-2ab2x-a2b2=0 の解となる。
(7) ① {ab(a+b)+(a2-ab+b2)√(2ab)}/(a2+b2),② 2mn(m+n)(2m+n)/(2m2+2mn+n2),③ 120/17
AF=a√(2(a2+b2))/(a+b)
EF=(a2+b2)/(a+b)
CF=2ab/(a+b)
(1) 証明
(2) 証明
(3) 証明
(4) 証明
(5) 証明
(6) 証明
(1) S=(a2+1)/(4(a+1)),a=√2-1のとき最小値 (√2-1)/2
(2) (a+b+√(a2+b2))/√2,6√2
(3) √3/3
45°
| (解) ∠AEC=∠AEF,∠ACB=∠ACFより点Aは△CEFの傍心である。 よって,EFの延長上の点をTとすれば,∠AFC=∠AFTである。 よって,∠EAF=∠AFT-∠AEF= ∠TFC- ∠FEC =(∠TFC-∠FEC)/2=(1/2)∠FCE=45° (参考) △ABCの1つの内角の二等分線とそれに隣り合わない2つの外角の二等分線は1点で交わる。 この交点を△ABCの傍心と呼ぶ。 |
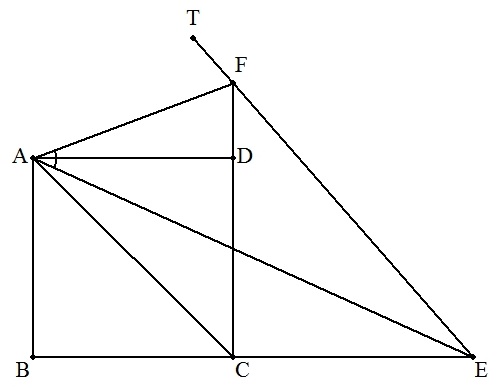 |
45°
(解) FD=BE+EC-CF=b(a+2b)
BE:CE=a:2b,CF:DF=a:bであるから
BE:CE=CF:2DFが成り立つ。
よって,∠EAF=45°である。
(1) k=(3√21-7)/10
(2) k=(23-12√3+9√13)/46
(1) AE=5a/6 (ヒント)103(2)
(2) r=a/4 ※正方形内の3円の半径はすべて等しい。
略 (ヒント)トレミーの定理
(1) √2-1
(2) √3-1
証明→こちら
(1) [a2-b2+c2+2(b-c)√{s(s-a)}]/(2a) ただし,s=(a+b+c)/2
(2) √{s(s-a)}
(3) {√s-√(s-a)}√{(s-a)(s-b)(s-c)}/a
(4) 順に,7/4,3/2,√15/8
(5) △ABDの内接円の半径:r1
(a,b,c)=(35,29,8)のとき,(BD,AD,r1)=(10,6,2)
(a,b,c)=(45,40,13)のとき,(BD,AD,r1)=(15,14,4)
(a,b,c)=(75,65,20)のとき,(BD,AD,r1)=(24,20,6)
(1) r12+ar1+r22=a2/4
(2) r1=(√3-1)a/4
(3) r1=(√6-1)a/10,r2=(√6-1)a/5
(1) r1={√(34+10√5)-√(5-2√5)}a/16
(2) r1={√(1314+502√5)-(13+5√5)√(5-2√5)}a/176,r2={√(6570+2510√5)-(25+13√5)√(5-2√5)}a/176
(1) r1=(√15-√3)a/8
(2) r1=(√30-√3)a/18,r2=(2√5-√2)a/6
(1) r1=(√7-√3)a/8
(2) r1=(√13-√3)a/20,r2=(√39-3)a/20
(1) √(10(5-√5))a/5(=1.051462224a)
(2) √(5(85+38√5))a/5(=5.830447378a)
解答→こちら
(1) 51°
(2) 90°×{(k-i)/m+(j-l)/n}
| (解1) |
対角線ACを引く。 △ACDを,Aを中心に時計回りに90°回転させ△AEBをつくる。 求める四角形の面積は,直角二等辺三角形AECの面積と等しくなる。 ECを底辺と見ると,底辺がBC+CD=6で, 高さAFは6÷2=3の三角形であるから 求める四角形ABCDの面積は 6×3÷2=9・・・(答) | 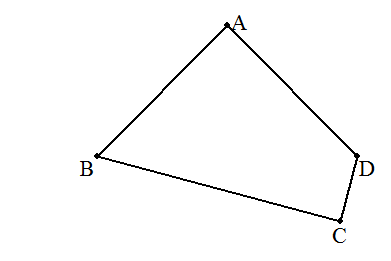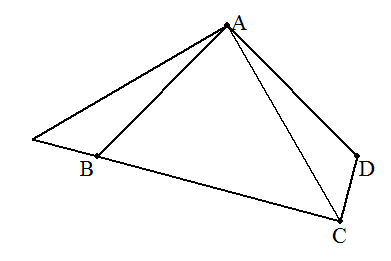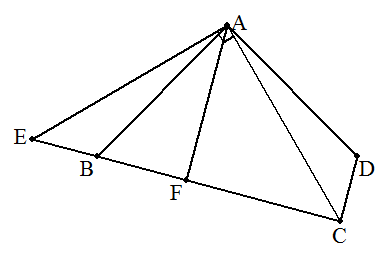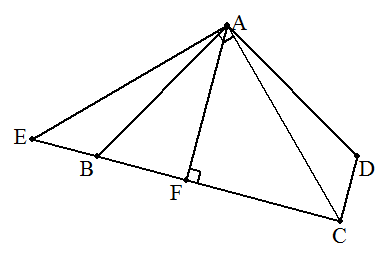 |
| (解2) |
四角形ABCDを,Aを中心に90°回転させ四角形ADEFをつくり, さらにAを中心に90°回転させ四角形AFGHをつくり, さらにAを中心に90°回転させ四角形AHIBをつくる。 正方形CEGIの一辺の長さは,BC+CD=6である。 求める四角形ABCDの面積は, 正方形CEGIの4分の1であるから 6×6÷4=9・・・(答) | 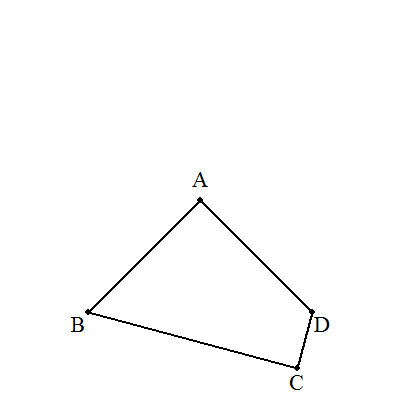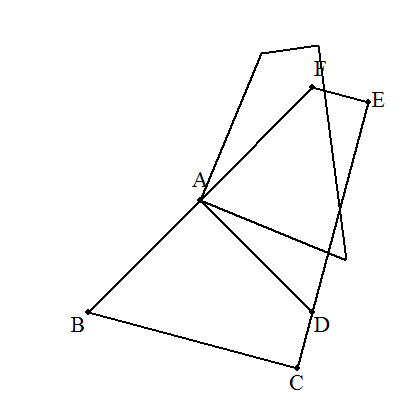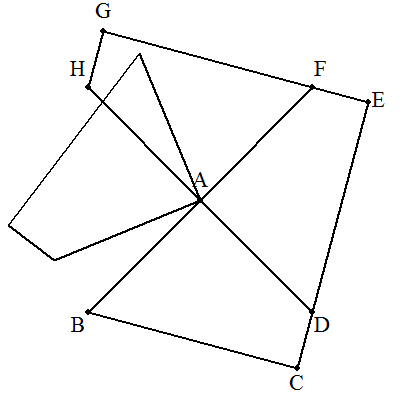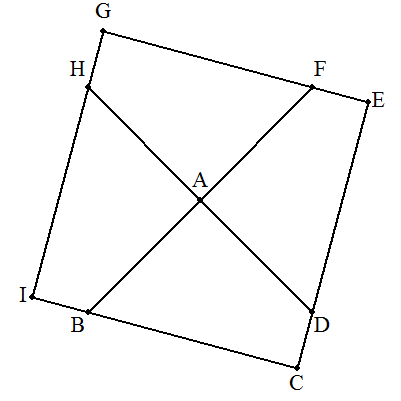 |
2つの解答を見てわかるように,∠ABC=60°の条件は使っていない。
∠ABCは45°と135°の間の角であれば何度でも答は同じになる。
(証)
| A,DからBCに下ろした垂線の足をそれぞれF,Gとする。 △BDGにおいて,BD:DG=BC:AF=2:1より∠DBG=30°(∵△ABCは直角二等辺三角形) ∠ABE=45°-30°=15°より ∠AEB=90°-15°=75°=∠CED(対頂角)・・・① △BCDは二等辺三角形であるから ∠BDC=(180°-30°)/2=75°=∠CDE・・・② ①,②より△CDEは底角75°の二等辺三角形となるから CD=CE(終証) | 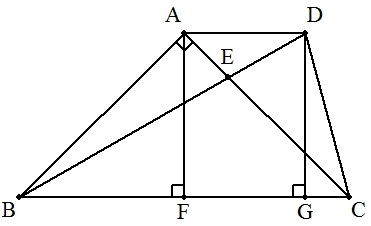 |
(証)
| BDの延長上に点Eを,DB=DE・・・①となるようにとる。 △ABD≡△AEDより,∠ABD=∠AED=∠DBCより AE∥BC(∵錯角が等しい) よって,四角形ABCEは台形となる。 さらに,∠AEB=∠ACBより,四角形ABCEは円に内接する。(∵円周角が等しい) よって,四角形ABCEは等脚台形となるので,対角線AC=BE=2BD(∵①より) したがって,BD=AC/2(終証) | 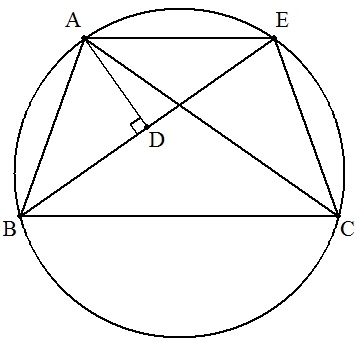 |
x=36°
(1) b2=c(a+c),b=6
(2) a2=(b+c)(b-c)2/c,a=35
(3) b2={c(a+2c)+a√(c(4a+5c))}/2,b=3√14
(4) a2=(b-c){-c(b+2c)+b√(c(4b+5c))}/(2c),a=(5√14)/2
(5) b=√(99+21√21)
(6) a=3√14/2
∠x=39°
|
(小学生向け) △CDAをCを中心にCDがCBに重なるまで回転させ,△CBEを作る。 CA=CEより,∠CAE=∠CEA=56° ∠BCA=∠CBE-∠CAB=95°-56°=39° (中学生向け) ∠B+∠D=180°より,四角形ABCDは円に内接する。 BC=CDより∠BAC=∠CAD=56°(円周角) ∠BCA=180°-(∠ABC+∠BAC)=180°-(85°+56°)=39° | 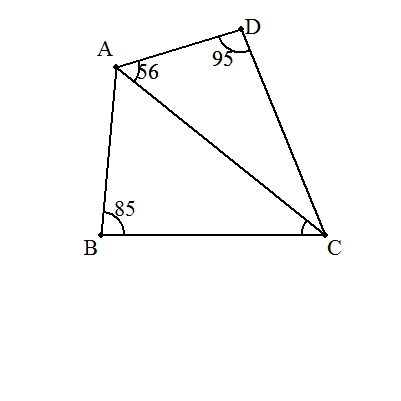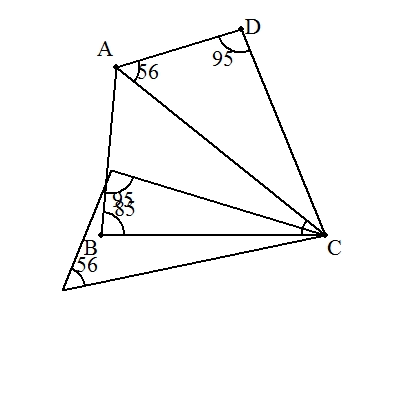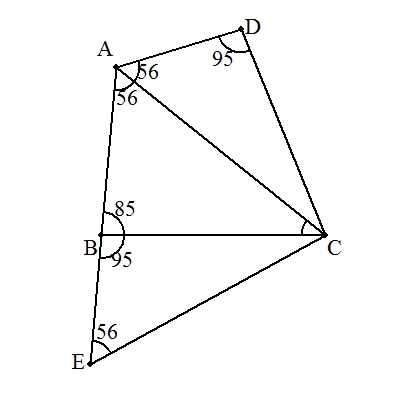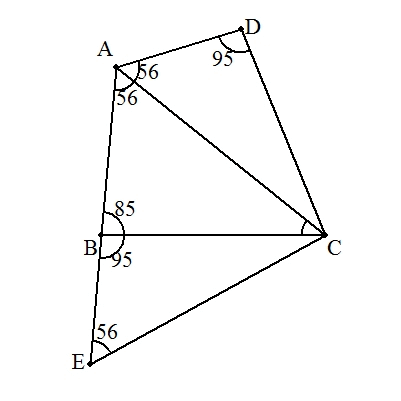 |
証明→こちら
DE=AB/2=5/2
(1) DCに平行で,ABの中点を通る直線とACとの交点が点Eとなる。
(2) √(4a4-3a2b2+b4)/(2a)
(3) √37/3
(1) a/2
(2) (√2-1)a(b2+c2-a2)/(a2+b2-c2)
(3) ac/(a+c)
|
(作図) 点Bから,直線l,mに下ろした垂線の足をそれぞれE,Fとする。 EF上に点Gを,EG=FBとなるようにとる。 このとき,AGと直線lとの交点をCとすればよい。 あとは,Cから直線mに垂線CDを引き,DBを引く。 (証明) AC+CD+DBのうち,CDの長さは一定であるから, AC+DBの長さが最小になる場合を考える。 図より,FBの長さをEGに移せば, AC+DB=AC+CG=AG 2点A,Gを直線でつないだとき,AC+DBは最小となる。 (補足)l上にC以外の点Pをとり,Pから直線mに下ろした垂線をPQとすると, AP+QB=AP+PG>AG=AC+DBとなり,AC+DBが最小となることがわかる。 (三角形の2辺の和の定理) 三角形において,2辺の和は,残りの辺より大きい。 | 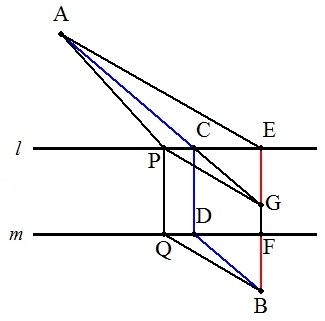 |
4(-358269+508774√3)/1531299
(=1.36604)
| (解説) 線分ACに関する点Pの対称点をQ, 線分ABに関する点Pの対称点をR, AC,ABとQRとの交点をそれぞれ D,Eとすれば,△PDEの周の長さ は最小になる。 | 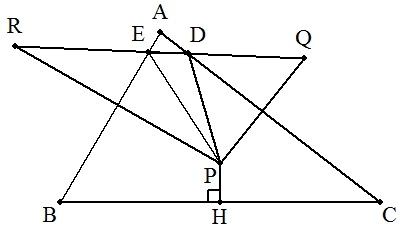 |
82°
(1) ①30° ②70°
(2) ①30° ②30°
40°
解答→こちら
AP=25/√129,BP=40/√129,CP=64/√129
(1) OD0=(an+bn)/(an-1+bn-1)
(2) CnDn=(b-a)√(an-1bn-1)/(an-1+bn-1)
(3) OCn=√{(an+1+bn+1)/(an-1+bn-1)}