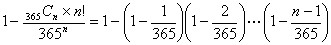
ここでn=20を代入する
=-(364÷365×363÷365×362÷365・・・×346÷365-1)=0.4114383836
と入力すると、オーバーフローなく計算できる。
省略
解答はこちら
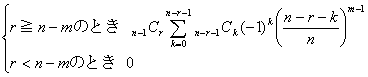
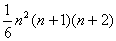
(1) sin2C:sin2B=c2(a2+b2-c2):b2(c2+a2-b2)
(2) (2S)3/{a2(b2+c2)-(b2-c2)2},Sは△ABCの面積
(3) 4abcS/{a2(b2+c2)-(b2-c2)2}
(4) (1) 114:125,(2) 864√6/239,(3) 420√6/239
n(n+1)(8n+1)π/6
r1:r2:r3:r4=12:20:15:10
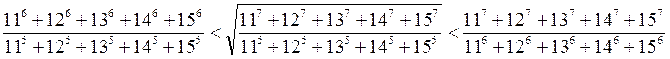
| (1) | 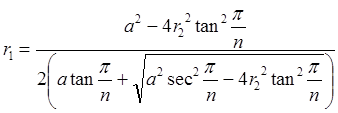 |
| (2) | 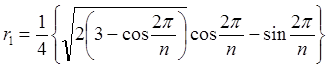 |
| (3) | 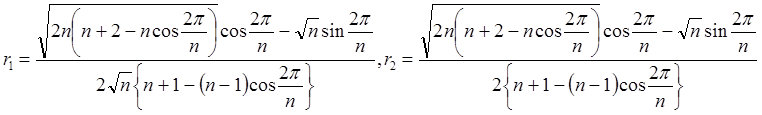 |
略
(ヒント)
AB=a,BC=b,CD=c,DA=dと置き,Rとrを求め,相加平均・相乗平均を使う。
| (1) | AF=√[(2a2+b2-b√{3(4a2-b2)})/2] a<bのとき,AF=(b√3-√(4a2-b2))/2 a>bのとき,AF=(√(4a2-b2)-b√3)/2 |
| (2) | AF=(3√3-√7)/2 |
| (3) | AF=2√2-√3 |
AF=[b√3-√(4a2-b2)+√{-12a2+2b2+16c2-2b√(3(4a2-b2))}]/4
AG=[-b√3+√(4a2-b2)+√{-12a2+2b2+16c2-2b√(3(4a2-b2))}]/4
※ c=aのとき,B問題67の問題となる。
AB=(r1+r2){r12+r22+(r1+r2)√(r12+r22)}/(r1r2)
(例)r1=3,r2=4のとき,AB=35
(1) (-3+2√2+√(20-14√2))a
(2) (5-3√2-2√(10-7√2))a
(1) 順に,21/4,12/7,7/3,16/21
(2) r2n-1=(21/4)×(4/9)n-1,r2n=(12/7)×(4/9)n-1
rk=2rsinθsinkθsin(k+1)θ/{sinθ+sinkθ+sin(k+1)θ}
答→こちら
8/9
| (解)円O1,O2の半径をそれぞれr1,r2とおく。 BC=BD+DE+EC =r1/tan(B/2)+2√(r1r2)+r2/tan(C/2) =aに a=5,r1=1/2,tan(B/2)=√{(1-cosB)/(1+cosB)}=1/2, tan(C/2)=1/3を代入すると, 3r2+√2√r2-4=0 √r2>0より r2=8/9・・・(答) | 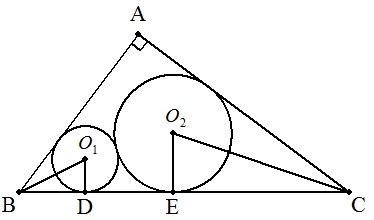 |
4ab√ab/(a+b)
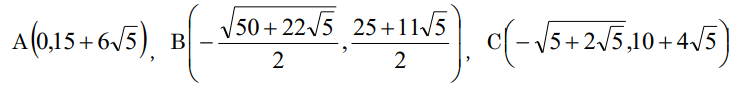
(1) A(23,33)
(2) m=127,n=125
(1) α5+β5+γ5=-p5+5p3q-5pq2-5p2r+5qr より明らか。
(2) α7+β7+γ7=-p7+7p5q-7p4r-14p3q2+21p2qr+7pq3-7pr2-7q2r より明らか。
(3) α9+β9+γ9=-p9+9p7q-27p5q2+30p3q3-9pq4-9p6r+45p4qr-54p2q2r+9q3r-18p3r2+27pqr2-3r3 であるから
rが3の倍数のとき,α9+β9+γ9は9の倍数,
rが3の倍数でないとき,α9+β9+γ9は9の倍数でない。
(4) α11+β11+γ11=-p11+11p9q-44p7q2+77p5q3-55p3q4+11pq5-11p8r+77p6qr-165p4q2r+110p2q3r-11q4r-33p5r2+110p3qr2-66pq2r2-22p2r3+11qr3 より明らか。
証明→こちら
(√6+√30)/24
(1) 1/4
(2) √10/10
(3) √21/14
(4) cos(π/n)/√(n+1)
(1) {7・2n-1-3(-2)n-1+8(-1)n-1}/12
(2) (2・4n-1-3n+1+9・2n-5)/6
(3) {20+15(-1)n+15・2n+1+(-2)n+1-3n+1}/60
解答→こちら
(1) √3/8
(2) (√6+√2)/16
(3) θ=5°
証明→こちら
証明略
12(61-6√61)/125
(1) θ=10°,50°,70°
(2) θ=5°,25°,35°,45°,55°,65°,85°
解答例→こちら
略証
公式:tanθ=tan3θtan(30°-θ)tan(30°+θ)に
θ=1°,2°,3°,・・・,10°を代入し,
辺々掛け合わせれば得られる。
なお,公式の証明は前問の解答を参照のこと。
(1) tanα=(b-a)/(a+b),tanβ=a/b
(2) CD=b(b-a)/(a+b),DA=a(b-a)√(a2+4ab+5b2)/{(a+b)√(a2+b2)},AC=(b-a)(a+b)/√(a2+b2),BD=2√2ab2/{(a+b)√(a2+b2)}
(3) AE=a(b-a)/√(a2+b2),BE=√2ab/√(a2+b2),CE=b(b-a)/√(a2+b2),DE=√2ab(b-a)/{(a+b)√(a2+b2)}
(4) △EBC=ab2(b-a)/{2(a2+b2)},四角形ABCD=ab2(b-a)/(a2+b2)
※四角形ABCD=2△EBC
APn2=knb2+(1-kn)c2-kn(1-kn)a2
※Stewartの定理あるいは余弦定理を使って,AP12=kb2+(1-k)c2-k(1-k)a2を利用する。
S=m!n!(β-α)m+n+1/(m+n+1)!
※解答→こだわり数学35のNo.4を参照せよ。
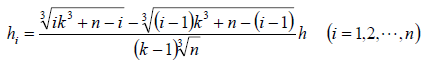
※解答→こだわり数学42を参照せよ。
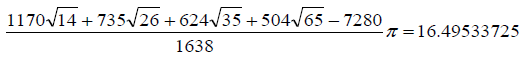
※解答→こだわり数学57を参照せよ。
(1) (n-1)n(n+1)(3n+2)/24
(2) (n-2)(n-1)n2(n+1)2/48
(3) (n-3)(n-2)(n-1)n(n+1)(15n3+15n2-10n-8)/5760
※解答→こだわり数学 9 を参照せよ。
(1)
M(a)について
a≦(-3-√33)/6のとき,-a3+3a
(-3-√33)/6<a≦0のとき,-a3-3a2+2
0<a≦1のとき,2
1<aのとき,-a3+3a
m(a)について, a≦-2のとき,-a3-3a+2
-2<a≦-1のとき,-2
-1<a≦(-3+√33)/6のとき,-a3+3a
(-3+√33)/6<aのとき,,-a3-3a+2
(2)
k<(18-2√33)/9のとき,0個
k=(18-2√33)/9,k>11/4のとき,2個
k=11/4のとき,3個
(18-2√33)/9<k<11/4のとき,4個
※解答→こちら
(1) 2015
(2) n+k
解答→こちら
解答→こちら
m3=163=4096
※因みに,n=66である。
n4
| (1) |
|
||||||||||||||||||||||
| (2) |
|