■趣味の数学問題集・Ａ問題の答

---

51. 
    

    (1)	88453+88453=176906
    (2)	3358×058=194764
    (3)	1154+1154=2308など17通り
    (4)	1278+3327=4605など106通り

52. 
    

    (1)	33541+33541=67082 33591+33591=67182 44513+44513=89026 44516+44516=89032 44531+44531=89062 44536+44536=89072 44615+44615=89230 44635+44635=89270 44651+44651=89302 の9通り
    (2)	11728+11728=23456 11792+11792=23584 11852+11852=23704 33546+33546=67092 33906+33906=67812 44518+44518=89036 44538+44538=89076 の7通り
    (3)	解なし

53. 
    

    (1)	6617×317=2097589
    (2)	33924+33924=67848

54. 
    144通り
    
55. 
    216通り
56. 
    省略。（Hint）a-b=-p,b-c=-qとおくとc-a=p+q
    （参考）
    (a-b)³+(b-c)³+(c-a)³=3(a-b)(b-c)(c-a)
    (a-b)⁵+(b-c)⁵+(c-a)⁵=5(a-b)(b-c)(c-a)(a²+b²+c²-ab-bc-ca)
    (a-b)⁷+(b-c)⁷+(c-a)⁷=7(a-b)(b-c)(c-a)(a²+b²+c²-ab-bc-ca)²
    
57. 
    {(10+6√2-5√3-4√6)/2}
    
58. 
    軌跡は定点（-4/5,-6）
    
59. 
    1/6
    （参考）⊿DEF/⊿ABC=r/(2R)である。
    
60. 
    r₀=12(-13+6√6)/47
    r₄=12(13+6√6)/47
    r₅=6(17+6√6)/73
    r₆=3(10+3√6)/46
    r₇=12(43+12√6)/985
    r₈=(8+3√6)/10
    （参考）こだわり数学の38.互いに外接する3つの円に外接及び内接する円などについて(PDF)
    
61. 
    (1)　
    (2)　
    （参考）こだわり数学の40.互いに共有点をもたない3つの円に外接及び内接する円について(PDF)
    
62. 
    (1)　略（ACの中点をLとすると，⊿LMNは二等辺三角形となる。）
    (2)　90°-(β-α)/2
63. 
    67.5°
    
64. 
    

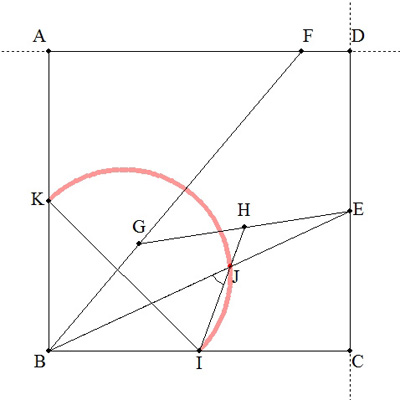
    (1) 45° (2) ABの中点をKとするとき，IKを直径とする半円。 ∠CBEの大きさにかかわらず，∠BJI＝45°となる。 解答→こちら

65. 
    
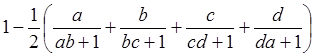
    解答→こちら
66. 
    (1)　αβγ(α－β)(αβ＋γ²)
    (2)　αβγ(α＋β)(αβ－γ²)
67. 
    (1)　V₁：V₂：V₃＝bc：ca：ab
    (2)　S₁：S₂：S₃＝bc(b+c)：ca(c+a)：ab(a+b)
    解答→こちら
68. 
    (1)　EG：GH ＝24：25
    (2)　IK：KJ＝15：56
69. 
    (1)　⊿DEF：⊿ABC＝11：35
    (2)　⊿PQR：⊿ABC＝4：27
    
70. 
    2：9
    解答→こちら
71. 
    17082÷5694=3
    20457÷6819=3
    20754÷6918=3
    24507÷8169=3
    27504÷9168=3
    15628÷3907=4
    28156÷7039=4
    36508÷9127=4
    34902÷5817=6
    21658÷3094=7
    28651÷4093=7
    65128÷9304=7
    65821÷9403=7
    
72. 
    解答→こちら
73. 
    n=972，972³-972²= 917385264
    解答→こちら
74. 
    証明→こちら
75. 
    内接円の半径r＝4γ²(αβ－γ²)，外接円の半径R＝(α²＋γ²)(β²＋γ²)
    【補足】この結果から，α，β，γがα＞β≧γを満たす正の整数であれば，r，Rも正の整数となることが分かる。
    【具体例】こちら
    
76. 
    14
77. 
    (1)　(2√2/7)a
    (2)　((4√3-3)/13)a
    (3)　(16√17/85)r
    (4)　2(160+55√5-4√(1105+262√5)}a/419
    (5)　4(4-√3)a/13
    
78. 
    解答→こちら
    
    
79. 
    (1)　15
    (2)　(p+q)(p+q+√(p²+6pq+q²))/4
    解答→こちら
80. 
    (1)　(-9+6√2-5√3+6√6)a²/24
    =0.230081908045552a²
    解答→こちら
    (2)　(1+√3)a²/12
    
81. 
    72
    

    （解説）ADの延長とBCとの交点Eを中心に，⊿ECDを時計回りに180°回転させると， 求める面積は等辺12の直角二等辺三角形となる。 よって，その面積は　122÷2＝72 ※この問題の解法は，初等数学の会通信第19号（2003/8/1　松田康雄発行）で知りました。 解答→こちら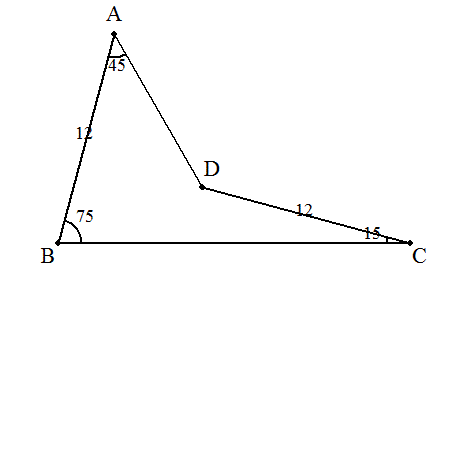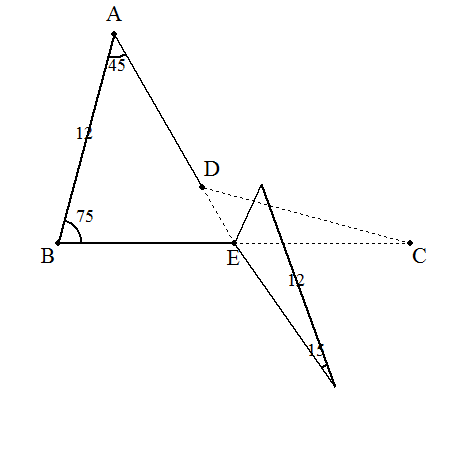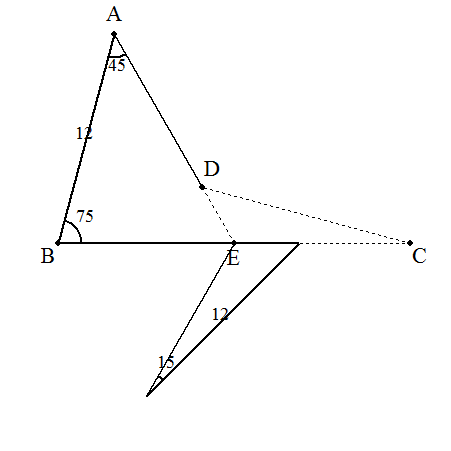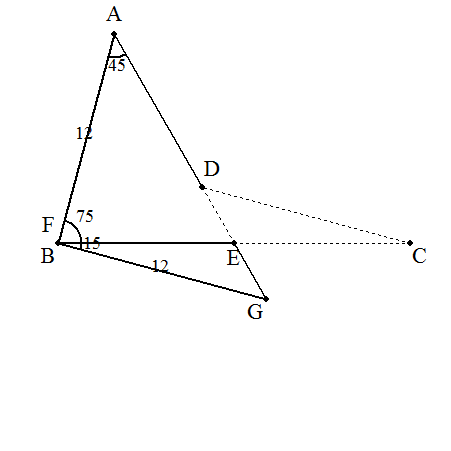

82. 
    √97/7
    （ヒント）
    α＋β＋γ＝360°のとき，
    cos²α＋cos²β＋cos²γ＝1+2cosαcosβcosγを使うか，
    和算での六斜術を使う。
    解答→こちら
83. 
    √(281-20√55)/3
    解答→こちら
    別解は問題B58(3)を参照せよ。
    
84. 
    ｛3√3-√7＋√(70-6√21)｝/2
    解答→こちら
85. 
    (1)　√{(13+√23)/2}
    解答→こちら
    (2)　√{(13-√23)/2}
    (3)
    　
    （参考）
    正方形の1辺が正の整数になる例
    (ア)　E：正方形の内部
    　AE＝25，BE＝51，CE＝53のとき，AB＝52
    　AE＝25，BE＝52，CE＝53のとき，AB＝51
    　AE＝89，BE＝45，CE＝91のとき，AB＝116
    (イ)　E：正方形の外部
    　AE＝35，BE＝44，CE＝97のとき，AB＝75
    
86. 
    証明→こちら
    （補足）
    2円C，Aの共通外接線の交点，2円A，Bの共通内接線の交点，2円B，Cの共通内接線の交点も1直線上にあり，
    2円A，Bの共通外接線の交点，2円B，Cの共通内接線の交点，2円C，Aの共通内接線の交点も1直線上にある。
    
87. 
    75/4
    解答→こちら
88. 
    (1)　2
    (2)　√3/3
    (3)　(41√21-8√39+11√111-2√10101)/54
    解答→こちら
89. 
    (1)　(2√2)a/(3n+1)
    (2)　(√3)a/(2n+√3)
    (3)　8nr/√{(5n²+2n+1)(5n²-2n+1)}
    (4)　2√(5+√5)a/√[25-11√5+{-10+6√5+4√(130-58√5)}n+{17-3√5+4√(10-2√5)}n²]
    (5)　(4√3)a/√{1+(2+4√3)n+(13+4√3)n²}
    　(1)～(3)の解答→こちら
90. 
    

    （作図） OAの垂直二等分線MNを作図する。 ただし，MはOAの中点で，NはMO＝MNとなる点である。 次に，Oを中心に半径ONの円を描き，OA，OBとの交点をそれぞれC，Dとする。 このとき，弧CDで扇形の面積は2等分される。 （証明）今，OA＝2a とすると，OM＝a ，ON＝(√2)a となり， ∠AOB＝b° とおくと， 扇形AOBの面積＝π(2a)2×(b/360)＝πa2b/90 ， 扇形CODの面積＝π｛(√2)a｝2×(b/360)＝πa2b/180 であるから （扇形AOBの面積）：（扇形CODの面積）＝2：1 よって，弧CDは扇形AOBの面積を2等分する。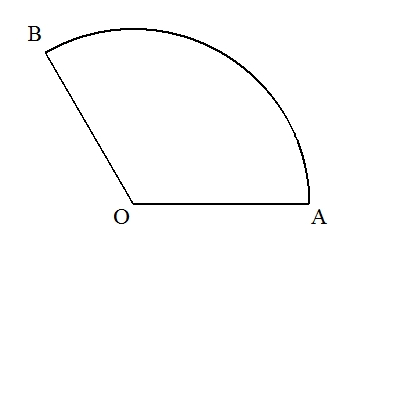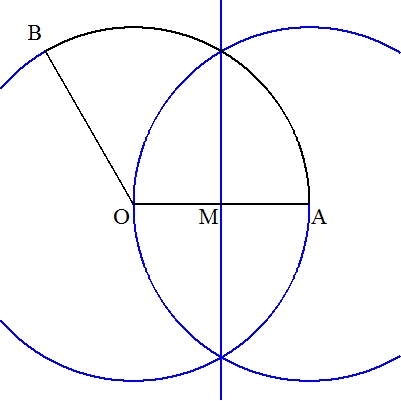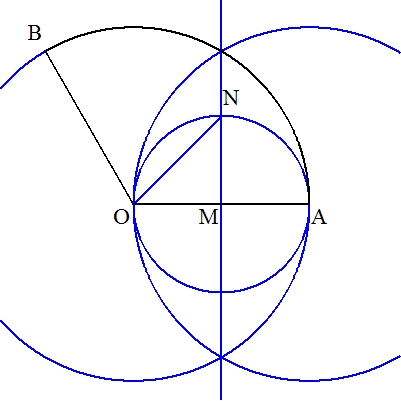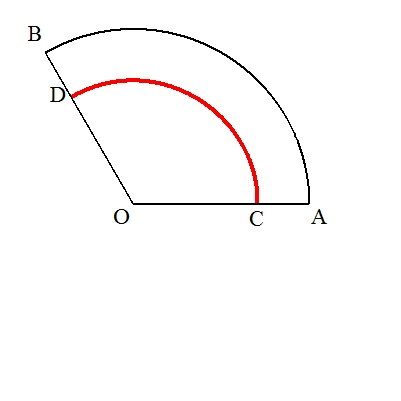

91. 
    解答→こちら
92. 
    解答→こちら
93. 
    証明→こちら
94. 
    
    
95. 
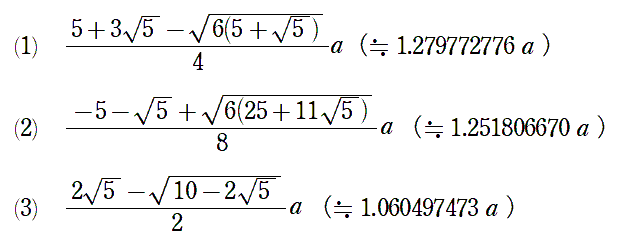
    (1)　45°
    (2)　DF＝b(a+2b)/(a+b)
    解答→こちら
    
96. 
    (1)　1
    (2)　(1+√3)/2
    (3)　{10+5√3+√(25+10√5)}/10(=2.554216364)
    (4)　√{15+5√3+3√5+√15+(1+√3)√(10-2√5)+(2+2√3)√(10+2√5)}/2(=3.919552136)
    (4)　
    
97. 
    (1)　（略証）
    ∠FAI＝∠FDI＝90°であるから，四角形AFDIはFIを直径とする円に内接する。
    ∠AFI＝∠ADI＝45°であるから，△AFIは直角二等辺三角形となる。
    よって，AF＝AI
    (2)　（略証）
    △ABC，△DBA，△DACはそれぞれ相似で，△ABC＝△DBA＋△DACである。
    よって，△ABC，△DBA，△DACの内接円についても相似であるから，
    △DBAと△DACの内接円の面積和は△ABCの内接円の面積に等しい。
    
98. 
    (ps+qr)/√{2(p²+q²)}
    ただし，p²+q²=r²+s²
    （補足）BC=2√[{(p+q)²s²+(r+s)²q²}/{2(p²+q²)}]
    （例）
    (p,q,r,s)=(8,1,7,4)のとき，GD=3√(13/10)，BC=2√(109/10)
    (p,q,r,s)=(9,2,7,6)のとき，GD=2√(34/5)，BC=4√(37/5)
    (p,q,r,s)=(11,2,10,5)のとき，GD=3√10/2，BC=√82
    (p,q,r,s)=(11,3,9,7)のとき，GD=4√(13/5)，BC=2√(229/5)
    (p,q,r,s)=(12,1,9,8)のとき，GD=21√(5/58)，BC=2√(2221/58)
    
99. 
    (1)　17
    (2)　686/345
    
100. （略証）正方形の1辺の長さをa，BE＝ax(0<x<1/2)とおくと，
     

     (1)	BG=IM=√(1-2x)a GL=DI={1-x-√(1-2x)}a/x LC=IH=√(1-2x){1-x-√(1-2x)}a/x
     (2)	(1)より，LC・BC=BG・GLが成り立つ。